基于SPC的高炉炉况异常检测研究

肖维民， 臧 俊， 袁志祥， 任诗流

安徽工业大学 计算机科学与技术学院，安徽 马鞍山 243032

1 引 言

钢铁工业是我国国民经济的基础产业，也是我国发展现代化建设的重要角色之一。高炉炼铁是钢铁工业中必不可少的关键部分，它不仅在我国炼铁工艺中占据绝对主导地位，同样也处于世界炼铁工艺的主体地位[1]。在高炉冶炼过程中，原燃料条件、送风制度、装料制度、造渣制度等因素中任何一个的变化都会导致炉况出现或大或小的波动。若高炉长时间处于异常状态，轻则造成铁水质量异常，产能损失，重则严重浪费人力、物力，同时安全风险高，易出现安全事故。因此，对高炉炼铁过程的炉况进行实时监控和预警，降低高炉出现异常炉况的概率从而预防高炉事故的发生，对钢铁行业来说有着重要的意义[2]。

不同的高炉类型、高炉的不同时期、不同高炉冶炼特点的不同，以及其高炉冶炼具有滞后性，所以高炉冶炼是一个复杂多变的物理化学过程。高炉可以看作是一个“黑匣子”，操作者只能通过监控和分析高炉各项参数的变化对高炉的生产过程进行评估，而操作者自身的经验水平、主观认识都不相同，这使得对高炉炉况的认识缺乏科学的方法。因此，科学、客观地判断炉况是炼铁工作者急需解决的课题。而早在20世纪80年代，日本首先开发出了高炉专家系统，日本川崎的GO-STOP系统通过8个高炉指数采取信息，构建了专家经验规则，对高炉冶炼过程进行评判[3]。现代大多数高炉专家系统都采用了GO-STOP系统的理论基础。黄波[4]等在武钢应用专家系统的前提下，于2005年根据多变量技术对高炉生产过程中的过程参数进行处理和数据分析。该方法有效地预判了炉温的变化趋势，也能提前2 h对铁水硅含量进行预报。

此外，随着技术日新月异的发展，基于机器学习的高炉炉况检测方法也有了很大的发展，取得了较多的研究成果。2010年，Tian[5]等将引导聚集算法和SVM算法集成，建立了一种新型高炉炉况诊断系统。该方法证明了SVM集成方法的性能要优于单一SVM方法。2011年，Liu[6]等改进DPSP算法加以优化LS-SVM算法的性能，阐述了一种基于成本意识的LS-SVM多类分类方法。该方法加快了处理速度，优化了分类精度，具有良好的适应能力。2020年，陈伟[7]等以高炉冶炼原理和专家经验为基础，通过线性规划和BP神经网络等技术方法，开发了炉料结构智能优化系统。在保证烧结矿质量和铁水产能前提下，降低了炼铁成本。

但以上方法都存在一定的不足之处。专家系统是有针对性地去解决部分问题；机器学习方法需要大量的高炉故障数据作为训练集，才能保证其准确率。然而高炉实际生产中发生异常的次数不多，且历史故障数据保存不完整，因此很难提供大量的故障数据作为训练集。相比之下，基于统计分析的方法优点在于不需要了解很多的机理知识和过程的前因后果关系，且对异常数据没有过多的要求。因此，本文结合高炉数据的特点，调整和改进主元分析算法(Principal Component Analysis，PCA)和统计过程控制方法(Statistical Process Control，SPC)，构建高炉炉况异常检测模型，通过离线数据模拟和在线运行进行实验。结果表明，本方法可快速监测高炉炉况，减少高炉工长自身主观意识，对保持高炉顺行提供了重要的保障。

2 PCA算法

PCA是一种常用于高维数据降维的数据分析算法。PCA保留了绝大部分主要信息，减少噪声干扰和去除一些不重要的特征，从而达到加快数据处理速度的目的。

对训练集进行PCA前，首先要对训练集进行中心化处理，均值必须从训练集计算而来。假设中心化后的数据为矩阵X(M×N),其中M为变量数目，N为训练集的样本数目，如下：

(1)

计算M个变量的相关系数矩阵R=(rij)(MN)，rij是原第i个变量和第j个变量的相关系数。计算公式如下：

(2)

系数矩阵R的特征值通过特征方程|λi-R|=0得到，并对其降序排列，λ1≥λ2≥…≥0；继而得到相应的特征向量e，最后，主元可以表示如下：

(3)

计算各个主元的贡献率和累计贡献率，第P个主元贡献率计算公式如下：

(4)

则前P个主元的累积贡献率计算公式如下：

(5)

累计贡献率越大，说明新的向量空间保留了越多的数据信息，一般当累计贡献率达到或大于85%时，可取这些成分代替原始向量空间[8-11]。

PCA模型一般使用T2统计量或SPE统计量对过程进行故障判断。其中T2统计量和SPE统计量的计算公式如下：

T2=zTS-1z

(6)

SPE=‖(I-PPT)X‖2

(7)

其中，z为主元向量，S=diag(λ1,λ2，…,λi)，S-1表示对矩阵中的非零元素取-1指数。X是新样本归一化后的数据。

若样本近似高斯分布，T2统计量可作为服从F分布，T2统计量和SPE统计量的控制限公式如下：

(8)

(9)

3 SPC基本原理

SPC最早是由美国的Shewwhart W A博士提出，并率先使用的控制图理论。但SPC真正得到发展和应用是在20世纪70年代，战后经济极度萎缩的日本采用SPC快速恢复了经济，并跃居全球质量和生产率的领先地位。自此，SPC开始大规模应用到制造业中，并逐渐成为企业中不可缺少的工具和质量保证手段[12]。美国著名的质量管理大师 Joseph h Juran说：“21世纪是质量的世纪[13]。”

SPC借助数理统计的方法对过程中的信息和数据进行监测，而过程中的数据一定会出现变差，SPC关注的是变差。将变差数据用图表的形式表现出来可直观看出一定的规律，从而有一定的预警作用。SPC主要采用控制图理论预防生产过程中错误的发生，拉依达准则是控制图理论的判定方法，由上控制限(Upper Control Limit，UCL)、下控制限(Lower Control Limit，LCL)和中心线(Center Line，CL)，并有按时间排序的样本数值的序列构成[14-16]。

控制图根据不同的数据类型可分为计数型和计量型，不同的情况使用不同类型的控制图。针对高炉生产过程中质量特性数据多、获取费时且花费成本也很高的问题本文采用单值-移动极差图中的单值控制图对高炉炉况的测量值进行监测。单值控制图控制上限和控制下限计算公式如下：

(10)

(11)

单值移动极差图将数据按时间序列标记在图上，便于迅速发现过程中的异常波动，并对其采取相应的措施，这很适合高炉过程的实际应用情况。而另一方面将单值控制图和基于PCA的T2统计量控制图相结合，二者共同决策出什么因素更为主要地导致了高炉炉况的波动。

4 基于现场数据的离线测试

4.1 数据预处理

本文的实验数据来源于某钢铁厂的一座2 500 m3的2号高炉。在高炉炼铁过程中每5 s对其过程数据进行采集，含有15个高炉炉况主要参数，一天共17 280条数据。具体参数如表1所示。本文选用了从2019年1月10日到2月10日，共32天的数据。

表1 2 500 m3高炉生产参数

这些高炉生产参数从自身来说存在着高耦合、非稳态、非高斯的复杂多样性数据，影响高炉炉况的因素众多且关系复杂。利用本文第2节中的PCA算法步骤，基于以上15个变量参数，对其进行降维处理。在保留多数信息的情况下用少量的几个综合变量取代原变量参数进行分析，其结果如表2所示。

表2 降维后的主元贡献率

由表2可看出，前6个主元已经包括了原数据的88%的信息，根据主元分析理论，已经可以通过前6个主元来代替原始数据集研究高炉炉况的原因。同时也可得到15个变量和6个主元之间的关系，具体如表3所示。

表3 主元系数矩阵

在实际生产中，由于每个主元都有15个影响因素，很难直接监测到主元，且当某个主元出现异常时，很难对其调整，因此，将每个主元中影响系数最高的变量作为该主元的关键因素。由表3可知，风温、风机风量、K值、冷风流量、煤气利用率和炉顶压力分别为对应前6个主元的关键控制参数。

4.2 构建控制图

根据上一小节得到的前6个主元，通过式(6)、式(8)计算出T2统计量的控制上限，并构造出控制图，如图1所示。

图1 T2控制图

由图1可看出，共有17个样本点不在控制界限内。但是这仅仅只能得出哪些时刻样本是否处于控制界限内，但无法具体看出是哪些变量影响了样本点，导致不受控制。因此，根据式(10)、式(11)再对以上6个影响主元的关键因素构建单值控制图。

由图1—图6分析，图1中的第3、4、5样本点出现了失控情况，而在图2中，炉顶压力单值控制图也出现了失控情况，说明炉顶压力在样本点3、4、5的失控状况产生了很大的影响，而在样本点3中，图6中K值也出现失控情况，说明K值也对该点失控也有一定的影响。通过分析，T2统计量是各变量影响的最终结果，因此，可通过观察该值来判断高炉炉况是否处于失控状态，若发现某个时刻的T2统计量超出控制限，则查看各变量的单值控制图，从而达到确定某个因素导致的高炉炉况不在控制范围内。

图2 炉顶压力单值控制图

图3 煤气利用率单值控制图

图4 冷风流量单值控制图

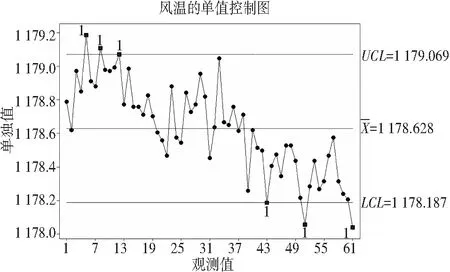
图5 风温单值控制图

图6 K值单值控制图

5 结束语

通过某钢铁厂历年生产数据，采用SPC中的T2控制图和单值控制图建立了高炉炉况异常监测模型，T2控制图主要监测高炉炉况的变化情况，单值控制图主要提供高炉工长分析什么因素导致的炉况波动，二者相互起到了互补作用，可以对高炉过程控制参数进行监控并建立起相关标准值，有效地改善了某钢铁厂高炉体检制度的全新体检标准。同时将该模型应用到了基于Spark的大数据平台中。根据实时运行参数与建立起来的标准值进行对比，更为直观地表现出高炉顺行状态。最后形成的参数监控模式更为有效地监控高炉炉况，保证了最后的产品质量的稳定性。本文证实了SPC技术在高炉冶炼过程在线实时监测的可能性，为钢铁企业把握铁水质量提供了一种新思路。