多目标博弈加权纳什平衡点集的通用稳定性
杨 林, 丘小玲
贵州大学 数学与统计学院,贵阳 550025
1 引 言
Von Neumann和Morgenstern在1944年完成的论文《博弈论与经济行为》,把博弈论研究推向系统化和公理化;1950年,Nash在论文《Equilibrium Points Inn-Person Games》中提出Nash平衡的概念,内涵是在其他局中人不改变当前策略时,局中人独自改变自己的策略并不能获得比当前更大的收益,Nash平衡的研究逐渐成为博弈论研究的核心;多人多目标非合作博弈模型的建立和Pareto-Nash平衡策略的提出扩展了博弈论研究领域,多目标博弈也更好地应用于现实生活中,引起很多学者的关注和研究,并取得很多显著成果。
文献[1]利用不动点方法研究n人多目标博弈的Pareto-Nash平衡点和加权纳什平衡点的存在性,并给出了Pareto-Nash 平衡点存在的几个充分条件,同时阐明了Pareto-Nash 平衡点与加权纳什平衡点的关系,为以后学者的研究提供了理论依据和方法的实现;文献[2]受文献[1]启发,从不动点理论(Fan-Glicksberg不动点和Fan-Browder不动点)和Ky Fan 不等式两种途径研究多目标博弈的Pareto-Nash平衡点和加权纳什平衡点的存在性,建立了在加权后支付函数连续性和凹性条件下多目标博弈的Pareto-Nash 平衡点和加权纳什平衡点的存在性结果。关于平衡点的稳定性,许多研究学者已经取得一些成果,文献[3]利用集值分析工具建立了非线性问题解集的通有稳定性框架,讨论了多目标博弈弱Pareto-Nash平衡点的通有稳定性;文献[4,5]研究了多目标博弈弱Pareto-Nash平衡点的本质连通区及向量拟平衡问题本质解和本质连通区;文献[6-13]得到了一些关于通有稳定性的研究成果。
本文的工作是构建伪连续向量值支付函数的博弈问题空间,给出加权Nash平衡点的定义,建立伪连续向量值支付函数下多目标博弈的问题空间,并讨论博弈加权纳什平衡点的存在性,通过定义博弈的集值映射,应用相关定理和引理证明集值映射是非空的、凸的、usco映射;应用Fan-Glicksberg不动点定理、Fort 定理以及本质平衡点定义,讨论权向量和支付函数及策略集三者同时扰动下加权纳什平衡点集的通有稳定性情况。
2 预备知识
本节先回忆一些定义和定理,给出文中需要的若干引理。
定义1[3]设X,Y是两个拓扑空间,集值映射F:X→P0(Y),其中P0(Y)表示Y的所有子集的集合,对x∈X,有
1) 如果对Y中的任意开集G,G⊃F(x)(或G∩F(x)≠∅),存在x的开邻域O(x),使得∀x′∈O(x),有G⊃F(x′)(或G∩F(x')≠∅),则称集值映射F在x处是上半连续的(或下半连续的);
2) 如果F在x处既是上半连续的又是下半连续的,则称集值映射F在x上是连续的;
3) 如果∀x∈X,集值映射F在x上是连续的(或上半连续的,或下半连续的),则F在X上是连续的(或上半连续的,或下半连续的);
4) 如果∀x∈X,集值映射F是上半连续的,并且F(x)是非空紧集,则称集值映射F是usco映射。
设Y是Hausdorff拓扑空间,Q⊂Y,如果Q包含一列在Y中稠密开集的交,称Q是Y中的一个剩余集(residual set)。
定义2[5]设X是一个拓扑空间,f:X→R是一个实值函数,有
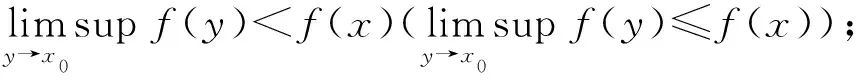
2) 称f在X上是上(弱)伪连续的,如果f对每一个x∈X都是上(弱)伪连续的;

4) 称f在X上是下(弱)伪连续的,如果f对每一个x∈X都是下(弱)伪连续的;
5) 称f在x∈X处是(弱)伪连续的,如果f在x∈X处既是上(弱)伪连续的又是下(弱)伪连续的;称f在X上是(弱)伪连续的,如果f在X中的每一点x∈X处都是(弱)伪连续的。
引理1 如果X是紧Hausdorff拓扑空间,函数f:X→R是上(下)伪连续的,那么函数f在X上可取到最大(小)值。
引理2 设X和Y是两个Hausdorff拓扑空间,而Y是紧空间,如果集值映射F:X→P0(Y)是闭的,则F在X上必是上半连续的。
定理1(Fan-Glicksberg不动点定理)[3]设X是一个Hausdorff局部凸空间E中的非空凸紧集,集值映射F:X→P0(X)在X上是上半连续的,∀x∈X,F(x)是X中的非空闭凸集,则存在x*∈X,使得x*∈F(x*)。
定理2(Fort定理)[3]设X是一个Hausdorff拓扑空间,Y是一个度量空间,集值映射F:X→P0(Y)是一个usco映射,则存在X中的一个剩余集Q,使得∀x∈Q,F在x处是下半连续的,从而是连续的。
定理3[3]设X是一个Baire空间,Y是一个度量空间,集值映射F:X→P0(Y)是一个usco映射,则存在X中的一个稠密剩余集Q,使得∀x∈Q,F在x处是下半连续的,从而是连续的。
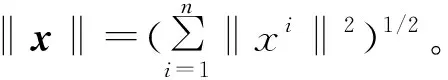
接下来考虑多目标博弈模型:
G={Xi,Fi}i∈N

在整篇文章中,给定m∈N+,记
其拓扑结构是由欧氏距离诱导得到的,内部记为

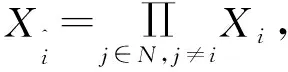


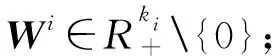
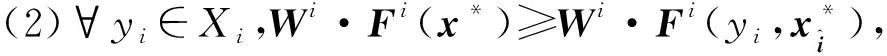
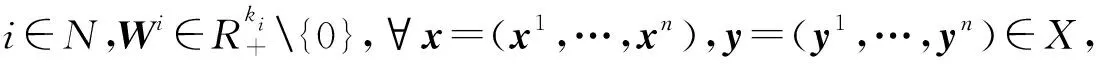
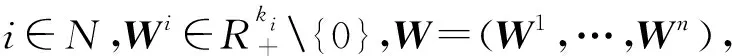
文献[1]的定理3考虑了SW(x,y)在X×X上连续和SW(x,y)关于y拟凹的条件下博弈G的关于权向量W的加权Nash平衡点,现在,考虑更一般的情况。
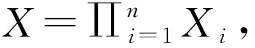
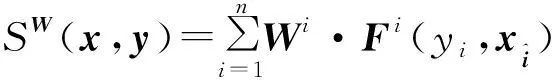
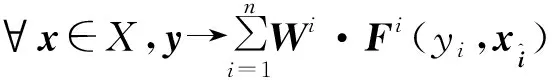
证明定义映射
由定理1和引理3,只需要证明集值映射MW(x)是上半连续的紧映射。
既然SW(x,y)在X×X上是伪连续的,根据引理1,可知MW(x)非空,首先证其是闭集,设{yn}⊂MW(x),yn→y0,需证明y0∈MW(x)。如若y0∉MW(x),则存在y1∈X,使得SW(x,y1)>SW(x,y0),由于SW(x,y)在X×X上是上伪连续的,有
矛盾。因此y0∈MW(x),即MW(x)为X中的闭子集,又由于X为紧集,所以MW(x)为紧集。
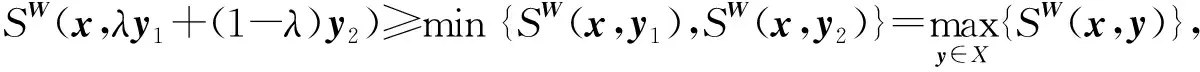
最后证MW(x):X→P0(X)是上半连续的,即证∀xn∈X,xn→x,有∀yn∈MW(xn),yn→y。需要证明y∈MW(x)。反证:假设y∉MW(x),则存在y1∈X,使得SW(x,y1)>SW(x,y),由于yk∈MW(xk),∀k∈N+,有SW(xk,yk)≥SW(xk,y1),由于SW(x,y)在X×X上是下伪连续的,令k→∞,有SW(x,y)≥SW(x,y1),矛盾。因此MW(x)是上半连续的。
根据Fan-Glicksberg不动点定理,存在点x*使得x*∈MW(x*),再由引理3,x*为博弈G的关于权向量W的加权Nash平衡点。
3 通有稳定性分析
如前所述,多目标博弈的平衡点存在但是未必是稳定的,并且多目标博弈的稳定性与研究条件有关,不同的条件下会有不同的结论。现在,分别构建多目标博弈在权向量扰动、权向量和支付函数同时扰动、权向量和支付函数以及策略集三者同时扰动情况下的博弈问题空间,定义相应的集值映射,并讨论加权Nash平衡点集在权向量和支付函数及策略集三者同时扰动情况下的稳定性情况。
首先在只考虑权向量扰动情况下构造问题空间:
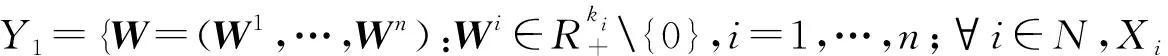
(1)
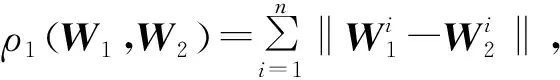
再考虑权向量和支付函数同时扰动情况下构造问题空间:
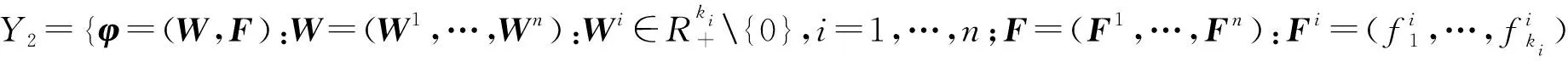
(2)
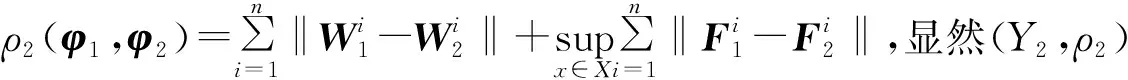
引理4 考虑权向量和支付函数同时扰动时,(Y2,ρ2)空间是完备度量空间。
证明设{φn}是Y2中的柯西点列,{φn}=(Wn,Fn),即∀ε>0,存在正整数N(ε),使得∀m,n≥N(ε),使得
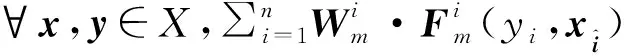
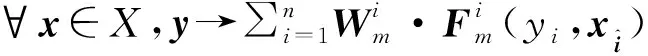


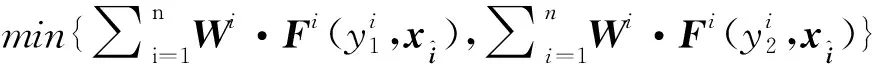

最后在考虑权向量和支付函数以及策略集三者同时扰动的情况下,构造问题空间:
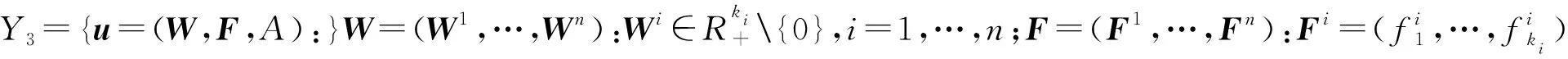
(3)
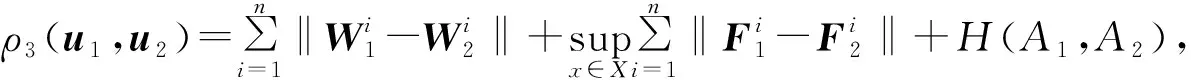
引理5 在权向量和支付函数以及策略集三者同时扰动情况下,(Y3,ρ3)空间是一个完备度量空间。
证明显然(Y3,ρ3)是一个度量空间,只需证明(Y3,ρ3)是完备的。记K(X)表示X中所有非空紧子集组成的集合,其拓扑是由E中范数诱导的Hausdorff距离,则(K(X),H)是一个完备度量空间。
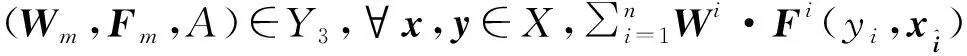
记Y3=Y0×K(X),且ρ3是由权向量和支付函数同时扰动情况下定义的距离和Hausdorff距离诱导得到的,既然权向量和支付函数同时扰动情况下的空间和(K(X),H)都是完备的,因此(Y3,ρ3)也是完备的。
引理6 设A和An(n=1,2,…)是Hausdorff拓扑空间X的所有非空紧子集,An→A,则
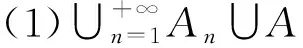
(2)如果xn∈An,xn→x,那么x∈A。
对于∀u=(W,F,A)∈Y,由u可以确定一个权向量为W、支付向量为F、策略集为A的多目标博弈,其中,∀i∈N,第i个局中人的向量值支付函数为Fi。这样,Y3可看作是由权向量和向量值支付函数以及策略集所确定的多目标博弈的集合,是一个博弈空间。∀u∈Y3,用N(u)表示权向量为W、支付函数向量为F、策略集为A的多目标博弈的所有加权Nash平衡点,根据定理4,N(u)≠∅,这样,定义了一个集值映射N:Y3→P0(X)。
定理5N在Y3上是一个usco 映射。
证明先证N(u)是紧集,由于N(u)表示权向量为W、支付向量为F、策略集为A的多目标博弈的所有加权Nash平衡点,对于∀u=(W,F,A)∈Y3,有
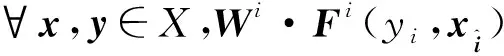
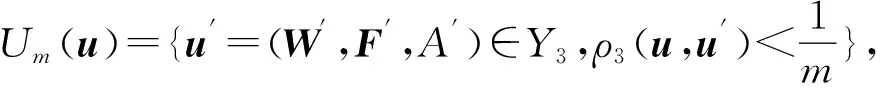
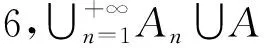
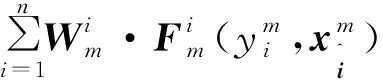
定义4[3]∀u∈Y3,x∈N(u),如果对x的任意开邻域U(x),存在u的开邻域O(u),使得∀u′∈O(u),∃x′∈N(u′),而x′∈U(x),则称x为多目标问题u的本质解。如果∀x∈N(u),x都是多目标问题u的本质解,则称多目标问题u是本质的;如果∃x∈N(u),而x是本质的,则称多目标问题u是弱本质的。
定理6 (1) 多目标问题u是本质的当且仅当集值映射N:Y3→P0(X)在u上是下半连续的;
(2) 多目标问题u是弱本质的当且仅当集值映射N:Y3→P0(X)在u上是弱下半连续的。
证明只证(1)。必要性:由于u∈Y3,对任何X中的开集G,G∩N(u)≠∅,在集合G中取x∈G∩N(u),则G是x的开邻域,因问题u是本质的,故x∈N(u)必是本质的,存在u的开邻域O(u),使得∀u′∈O(u),∃x′∈N(u′),而x′∈G。这样G∩N(u)≠∅,集值映射N:Y3→P0(X)在u下是下半连续的。
充分性:∀u∈Y3,∀x∈N(u),对x的任意开邻域U(x),有N(u)∩U(x)≠∅。因集值映射N:Y3→P0(X)在u下是下半连续的,存在u的开邻域O(u),∀u′∈O(u),N(u′)∩U(x)≠∅,取x′∈N(u′)∩U(x),则x′∈N(u),而x′∈U(x),且x是本质的,从而问题u是本质的。
定理7 ∀i∈N,存在Y3的一个稠密剩余集Q,使得∀u∈Q,多目标博弈的问题u都是本质的。
证明因Y3是一个完备度量空间,因而是一个Baire空间,而X是一个度量空间,根据定理5,集值映射N:Y3→P0(X)是一个usco映射,于是由Fort定理,存在Y3的一个稠密剩余集Q,使得∀u∈Q,集值映射N在u处是下半连续的。再由定理6,∀u∈Q,多目标博弈的问题u都是本质的。
定理8 ∀u∈Y3,如果N(u)={x},多目标博弈的问题u必是本质的。
证明对任何X中的开集G,G∩N(u)≠∅,因N(u)={x},则x∈G,从而G⊃N(u)。由定理5,集值映射N在u上是一个上半连续映射,存在u的开邻域O(u),使得∀u′∈O(u),有G⊃N(u′),于是G∩N(u′)≠∅,集值映射N在u上是一个下半连续映射。再由定理6,多目标博弈的问题u必是本质的。
注1 ∀u∈Y3,因Q在Y3中是稠密的,则u可以由多目标博弈的本质问题做任意的逼近。也即在Baire分类意义下,对大多数的多目标博弈问题u∈Y3,其问题u都是本质的,或者说多目标博弈问题u是本质的,是Y3上通有的性质。
推论1 ∀i∈N,存在Y3的一个稠密剩余集Q,使得∀u∈Q,其多目标博弈的弱Pareto-Nash平衡点都是本质的。
4 结 论
根据文献[3]提出的通有稳定性思想框架,在多目标博弈加权纳什平衡点在向量值支付函数连续条件下具有通有稳定性的基础上,提出向量值支付函数伪连续的情况,构建了问题空间,讨论了多目标博弈加权纳什平衡点的存在性结果,并应用定理与引理推导权向量和支付函数以及策略集三者同时扰动情况下加权纳什平衡点的通有稳定性情况,得出在Baire分类意义下,所构造的问题都是本质的,即多目标博弈加权纳什平衡点具有通有稳定性的结论。

