一种针对脑部图像分割强度不均匀性的改进方法
李 季, 胡锦萍, 乔 敏, 王 艳
1.重庆工商大学 数学与统计学院,重庆 400067 2.电子科技大学 信息与通信工程学院,成都 611731 3.重庆师范大学 数学科学学院,重庆 400067
1 引 言
众所周知,图像是用来反映外界事物的首要表现形式,外界的事物通过图像进入到人眼中,通过大脑的加工产生了对该事物的分析与了解。但是该种方式是最片面的,它还只停留于最浅显的部分。随着科学技术的发展,外界的所有物体都可以被转化为数字,通过数字图像将其记录储存到计算机中。这项技术的产生使得所有物体都有了具体的表示方式,也使得图像信息能够尽快地被捕获,促进了人类社会与科学技术的紧密联系。
要想将图像与技术结合起来需要借助一种工具——计算机视觉,即让计算机代替肉眼,对所得到的事物进行识别、探测、分析等任务。人类之所以能够轻易地读出图像的内容,是因为人体的各个器官都存在着相应的联系。按照人类视觉的功能,外界物体转化的数学图像处理算法可以分为许多种,这些分类在以后的数字图像发展过程中也起着至关重要的作用。
社会在不断地进步,科技也在不停地发展,图像分割已成为一个较为热门且急需深入研究的问题,它引领着医疗、军事、交通等多领域的发展。最简单的例子就是图像分割在医学领域的应用。
医学图像的组织分割非常重要,本文主要提出了一种针对脑部图像分割强度不均匀性的改进方法。磁共振成像(MRI)的分割结果通常受强度不均匀性的影响,这种不均匀性表现为组织的强度在整个图像域内呈现缓慢变化的状态。该性质的产生会使得不同组织的强度范围重叠,这就会产生严重的后果,如组织的误分割。因此,消除这种强度不均匀性,即偏移场的校正,就是MRI图像处理(如MRI定量分析)的第一步和关键步骤。要想校正偏移场,就需要先找出致使MR图像强度不均匀性的偏移场,然后再将图像分离,用其估计出来的偏移场得到偏移场的校正图像。在这里首先介绍一下活动轮廓模型。
活动轮廓模型可以分为两大类,分别是区域型和边缘型,本文主要对区域型模型进行阐述。传统的基于区域的模型非常依赖于图像强度均匀度,很明显不适合强度不均匀的图像。Chan等[1]提出了Chan-Vese(CV)模型或piecewise constant(PC)模型,用CV模型进行图像分割,原理就是利用了图像的全局信息,该模型虽然对边界辨识度低的图像放宽了限制,可以对该种图像进行分割,但并没有兼顾到强度不均匀的图像。同样地,PC模型也存在这一缺点。
为了获得分割结果和偏移场校正,人们提出了很多方法[2-7]。Li等[2-3]提出了一种基于变分水平集的局部加权K均值强度聚类(LIC)模型,用于图像分割和偏移场估计,在LIC模型中,图像强度被建模为真实图像和偏置场的倍数,真实图像近似于分段常数,偏移场缓慢变化,Zhou等[4]在LIC模型中引入了相关熵准则,以增加接近强度均值的像素权重;从全局角度出发,Li等[5]将图像分解为两个固有分量(MICO),即真图像和偏置场,并提出了用于偏置场估计和组织分割的MICO模型;Pham等[8]使用了模糊C均值(FCM)算法用于分割和偏移场估计;为了保证拥有一个平滑的偏移场,Vovk等[9]在能量函数中引入了平滑项,但平滑项系数的实用性会因此大大降低,使算法得不到广泛的应用。
本文基于模糊C均值(FCM)的能量最小化方法,将全局聚类和局部聚类相结合,用于磁共振(MR)脑图像的偏移场估计和分割。
单纯使用全局聚类或者局部聚类方法,会使得对其研究更加深入,但是在解决实际问题方面并不能得到很好的应用,要么造成图像分割的强度范围重叠化,要么不能将目标图像进行分割,本文的新方法不仅解决了这些问题,而且加快了图像分割的速度。
近年来,在图像分割领域涌现出大量的学者,尤其是在基于水平集的图像分割方法方面,他们将其用于医学图像中。但对于医学领域中病灶区域的图像分割,需要考虑强度不均匀性的影响。新方法可以解决这一困难,未来它将还会被应用到军事、航天等更加广泛的领域。
2 LIC和MICO模型介绍
2.1 LIC模型介绍
当把图像数字应用在现实生活中,就会出现灰度不均匀的现象,在面对这种的情况时,曲线演化过程就会出现误分割现象。为了能够更好地解决这一类图像的问题,在文献[3]中,Li等人提出了一种图像分割和变分水平集的方法,这两种方法利用了强度不均匀性与偏移场估计的原理,强度不均匀性可以被定义为
I(x)=B(x)J(x)+N(x)
(1)
根据式(1)的模型,将偏移场估计B和偏移图像J当作图像I的两个分量,其中N是加性噪声。假设偏移场是平滑的并且变化缓慢的,在即给定点的足够小的圆形领域内,B可以看作常数,同样对于图像中的每一个对象I,J也可以看作成常数,J(x)≈ci,看作是磁偏场。在这里,需对原图像以及磁偏场做出如下假设:
(1) 因为磁偏场B的变化比较缓慢,可以使用一个常数来表示某一像素点及其邻域的磁偏场;
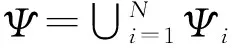
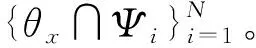
从假设(1)的条件可以推断出,所有圆形邻域中点y的偏置场B(y)与像素点x的偏置场非常接近,所以可以相互表示,其数学表达式:B(x)≈B(y),y∈θx;由假设(2)可以推断出,在第i个子区域θx∩Ψi中,可以用常数来表示偏置场B(y)和图像J(y)的乘积,数学表达式为B(x)ci≈B(y)J(y),y∈θx∩Ψi。此时,式(1)的模型可以表示为I(y)≈B(x)ci+N(x),y∈θx∩Ψi。
利用K均值聚类方法,此时LIC模型可以被定义为
当引入水平集函数φ时,上述模型可以改写成
B(y)ci|2Mi(φ(x))dx)dy
其中,M1(φ(x))=H(φ(x)),M2(φ(x))=1-H(φ(x)),是每个集群的成员函数。
此时最好的ci和b可以通过以下方法获得:
在上述的模型表示中,*代表的是卷积运算。
在用LIC模型对偏移场的评价中,使用的方法是加权K均值聚类,由于包括偏移校正标准,所以LIC模型的一个功能是可以先将那些强度不均匀性的图像结合起来,对于这些具有特殊性质的图像进行偏移场估计,但是该模型并不完善,对于图像的初始轮廓位置,鲁棒性并不强,尺度参数的选择完全依靠经验,针对严重的强度不均匀性的性质时,恒定的强度假设将不再保持不变。
2.2 MICO模型介绍
在磁共振成像(MRI)中,分割结果通常受强度不均匀性的影响,导致MRI该种性质存在有多种原因,B1(振荡磁场)和B0(主磁场)区域的不均匀性以及不同的患者都可能导致这种结果产生。该性质的产生会使得不同组织的强度范围重叠,这就会产生严重的后果,如组织的误分割。因此,在定量分析MRI数据之前的准备工作就是使用合适的方法消除强度不均匀性,如通过偏移场校正。
LIC模型,是从局部角度研究强度不均匀性,它对初始曲线敏感。这一缺点成为人们需要加紧改进的一个方面,许多学者在此也进行了大量研究。在文献[5]中,Li等提出了一种新的主动轮廓模型,即MICO模型来解决全局视角的MR图像的强度不均匀性,该方法是先将MR图像分解为两个乘法分量,一个分量表示该目标组织物理特性的真实图像,另外一个分量是强度不均匀性的偏场以及他们各自的空间特征。能量最小化过程可以同时实现偏移场估计和图像的组织分割,进行这一过程的目的是优化估计的两个乘法分量的MR图像。MICO模型在LIC模型的基础上有了很大的改进,它既可以实现偏磁场校正又能进行图像分割,大大地提高了模型的效率。有效的矩阵计算能够验证偏移场的数值稳定性,通过迭代可以优化偏场。并且给出公式中的能量在每个变量中都是凸的,这使得提出的能量最小化算法具有稳定性。同时,MICO模型也可以通过空间扩展到3D/4D图像组织分割。与其他的方法进行比较可知,MICO模型具有优越的鲁棒性和准确性。
然而就目前来看,MICO模型同时也存在了一些缺点,它还不能解决噪声等伪边界的问题。
MR图像I可以被表示为I(x)=B(x)J(x)+n(x),其中主要对B(x)进行说明,它是导致观测图像强度不均匀性的偏磁场。在上述介绍的MICO模型中,学者Li等人假设偏磁场B(x)通过能量最小化发现最佳偏移场估计B(x),和真实图像的像素点值J(X),定义如下:
在MICO模型中,为了确保偏移场的平滑度,通过给定一组光滑基函数g1,g2,…,gM, 有:
其中,ci是分段近似常函数,ui是二元隶属函数
G(x)=(g1,g2,…,gM)T,wT=(w1,w2,…,wM)T
最终,MICO模型中的能量函数可以写成:
3 模型的建立
如上所述,在本中主要考虑了LIC和MICO的优点,并提出了以下能量函数:
(2)
其中,α和β是两个正的常数。
3.1 能量最小化
在本文的MICO模型中,一共有4个变量,采用交替固定其中3个变量来进行最小化J(c,w,b,u) ,具体方式如下:
3.1.1关于变量c的优化
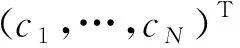
(3)
然后
(4)
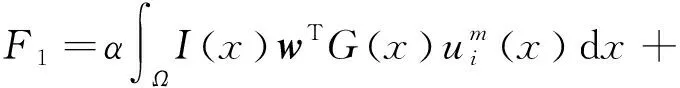
3.1.2关于变量w的优化和偏移场的计算
将变量c和u固定, 最小化关于w和b的能量项J(c,w,b,u), 可以得到:
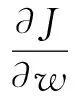
(5)
(6)
偏移场的估计可以由下列式子表示:
(7)
3.1.3关于变量u的优化
先考虑q>1的情况, 固定变量c,w和b,在u的约束条件下最小化能量项J(c,w,b,u) ,则
(8)
满足
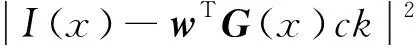
(9)
当q=1时,u可以表示为
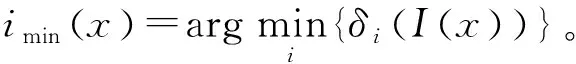
3.2 算 法
数值算法可以分成以下6个步骤进行 (当q>1时):
Step1 假设k=1 并且初始化u,c和b;
Step2 通过式(6)计算w;
Step3 通过式(4)计算c;
Step4 通过式(7)计算b;
Step5 通过式(8)计算u;
Step6 检查是否收敛,如果没有,令k=k+ 1并且返回重复Step2。
在上面描述的迭代过程中,4个变量中的每一个都与前一个迭代中计算的另外3个变量一起更新。因此,只需要初始化4个变量中的3个,如上面的迭代过程中的步骤1。
3.3 MICO模型引入正则化项的补充
在原来的MICO模型的公式中的隶属函数上添加一个正则化项。其公式实现为
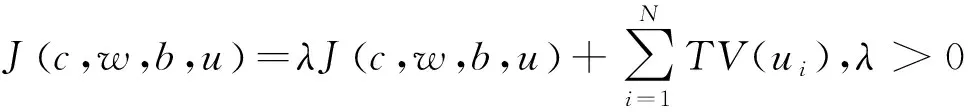
近年来,许多研究者提出了各种不同的数值格式[10]来解决图像分割中的变分问题,在0≤u(x)≤1的约束下,使用正则化项TV(u)来处理隶属函数。这些方法只能将图像分割成两个互补区域,分别用隶属度函数u和1-u表示。一般情况,要进行N>2区域的分割,需要使用3个或更多的隶属函数u1,u2,…,uN来表示。在文献[11]中,Li等使用Lions和Mercier[12]提出的算子分裂方法,开发了一种数值方案,解决了能量最小化问题,并对隶属函数进行TV正则化。能量J关于隶属函数u1,u2,…,uN的最小化可以使用文献[11]中描述的数值格式来实现。相对于变量c,w和b的能量最小化,都是独立于隶属函数的正则化项。
4 算法改进与实验对比分析
本文用来做测试的图像都真实的人工合成图像,使用的是 MATLAB 2020b (64 bit) ,电脑配置为Intel Core i7-8550U, 1.80 GHz and 1.99 GHz CPU, 16 GB RAM, Windows 10(64 bit)。在此次实验中,除非特别指出,设定参数为α=0.85,β=0.15,所有的数据来源为 BrainWeb: Simulated Brain Database (mcgill.ca), 其中包含 181个图像。 除非另做说明,所有图像都是使用的 40%的强度不均匀和 0% 的噪声。
为了验证本文提出方法的优势,拿MICO的分割结果与本文提出的新方法的分割结果作对比。
图1表示的是在No.40、No.50、No.60、No.80、No.100、No.120、No.130和No.140的分割图像与MICO模型作比对,可以明显地看到提出的新方法优于MICO的方法 (例如第一列的第二个和第三个图像,左下角分割明显优于MICO)。
为了更好地展示分割结果, 本文将脑灰质和脑白质分别分开来进行对比,如图2所示。
图2(a)为灰质的标准分割,图2(b)为MICO的灰质分割结果,图2(c)为提出的新方法的灰质分割结果,图2 (d)为白质的标准分割,图2(e)为MICO的白质分割结果,图2(f)为提出的新方法的白质分割结果。再利用DC度量(dice coefficient)来进一步说明分割结果,定义如下:
其中,S0表示目标分割结果,Sg表示目标标准分割。
DC值 (<=1) 常用来判断分割结果与标准分割结果的相似性,DC值越大,说明分割结果准确性越高。
通过比较图2中的灰质和白质的分割结果,根据MICO模型和提出的新方法分别得到其DC值,如表1所示,可以看到提出的新方法的DC值明显高于MICO方法得到的DC值。
表1中,第一行是对应图1的层数(从左至右),第二行和第三行分别是MICO和提出的新方法在灰质上的DC值,第四行和第五行是白质的DC值。

切片层数图像类别No.40No.50No.60No.80No.100No.120No.130No.140(a)原始图像 (b) MICO分割结果(c)新方法分割结果
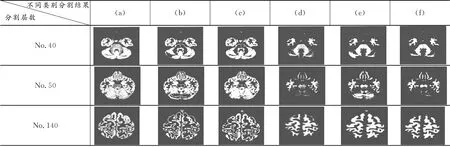
不同类别分割结果分割层数(a)(b)(c)(d)(e)(f)No.40 No.50No.140

表1 MICO和提出的新方法分别在灰质和白质下的DC值
图3中,分别选取20%和40%的强度不均匀和0%,3%,5%,7%和9%的噪声,验证在不同强度和不同噪声下两者的DC值比较结果。10种不同条件下,每一组包含不同的两个盒子,黑色是MICO的,灰色是提出的新方法,横坐标代表的是不同噪声和强度的组合,可以看出提出的新方法明显优于MICO的方法。
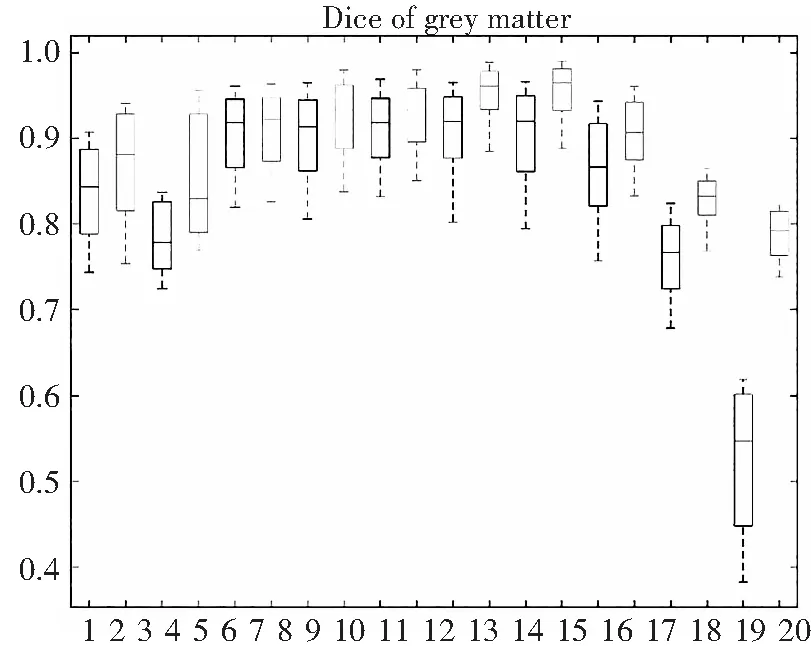
(a) 灰质DC值
5 结 论
MICO模型在能量最小化公式中用于MR图像的偏场估计和分割。通过矩阵和向量的演算,导出了计算偏场的有效能量最小化方案,并利用矩阵分析验证了偏场优化计算的数值稳定性。通过与其他方法在综合和真实MR数据上的评价和比较,证明了该方法的鲁棒性、准确性和有效性。并且该方法已成功地扩展到3D和4D的图像分割中,具有良好的结果。实验结果表明:该方法在分割精度和鲁棒性方面均优于目前常用的分割软件。
本文提出的新方法结合MICO模型的优点与不足,磁共振图像分割和偏场估计模型,基于模糊C均值(FCM)的能量最小化方法,将全局聚类和局部聚类相结合,用于磁共振(MR)脑图像的偏场估计和分割,得到了准确的分割结果,通过合成图像和真实图像的实验,验证得到的结果表明该模型是有效的。

