一种新的模糊决策树算法
——基于加权毕达哥拉斯模糊熵
刘 帅,吴 涛,2,方 越,胡皓玮
1.安徽大学 数学科学学院,合肥 230031 2.安徽大学 计算机智能与信号处理教育部重点实验室,合肥 230039
1 引 言
随着决策树在数据挖掘中的普遍运用,其在图像识别、机器学习、数据分类等方面均取得了显著效果。传统决策树算法如ID3算法和C4.5算法在处理不平衡数据时,分类效果不稳定,尤其在处理更复杂的模糊数据时不能实现更好的分类,所以将模糊理论和决策树相结合,模糊决策树(Fuzzy Decision Tree, FDT)被提出。
目前很多专家提出多种FDT算法, Wang等[1]提出基于模糊规则的模糊决策树算法,该模糊决策树的节点能够涉及多个特征模糊规则,证明其有更好的分类性能;翟俊海等[2]提出一种模糊粗糙决策树算法,结合了知识的粗糙度和数据的模糊性,该算法比模糊ID3算法有更高的分类精度;Zheng等[3]将隶属函数模型扩展到模糊随机森林中应用于风险识别和预测,结果表明该方法生成的决策树比经典决策树更准确;Wang[4]等提出决策树与模糊粗糙集中与属性约简融合的方法,该算法性能明显优于其他使用优势粗糙集的融合方法;Idris等[5]提出FID3算法,将模糊系统与ID3算法相结合,在乳腺癌数据集分类上有较高的准确率;Li等[6]将分类问题转化为模糊粒度空间来求解,将数据进行模糊粒度化,提出一种自适应全局随机聚类算法,认为选择扩展属性的标准是信息增益比,结果可知有较高的准确率和鲁棒性;Farna等[7]提出基于卡方值的多柔性模糊决策树,将传统卡方统计扩展到模糊卡方统计用于数据分类,实验结果表明该算法比传统卡方统计算法有更优的分类效果。
上述FDT算法把模糊粗糙领域概念与传统决策树结合构建模糊决策树,只是选择分裂属性的标准不同,每个样本属于节点的程度都是用隶属度来表示,但是无法获取样本数据对于节点非隶属度和犹豫度的信息,显然这些算法在实际中不能更好地全面获取数据信息,导致数据分类准确率不高。针对此,基于毕达哥拉斯模糊集(Pythagorean Fuzzy Set,PFS)理论,定义一种新的加权毕达哥拉斯模糊熵,并提出一种新的加权毕达哥拉斯模糊决策树算法(WPFDT),将PFS与FDT相结合,推导了WPFDT完整的构建过程,相较于传统FDT算法,WPFDT可以同时包含样本与节点之间的隶属度、非隶属度和犹豫度,可以更全面地描述节点中的模糊信息,从而提升数据分类准确性,该算法在处理具有模糊信息的实际问题中有更好的分类效果。
2 预备知识
在本节中,首先给出毕达哥拉斯模糊集的基本知识,然后介绍FDT的基本知识,最后介绍如何将连续数据转换成PFS的主要手段。
定义1[8]设X为论域,则称A={〈x,μA(x),νA(x)〉|,0≤μA2(x)+vA2(x)≤1,x∈X},μA(x),νA(x),πA(x)∈[0,1]为PFS,其中μA(x),νA(x),πA(x)分别是A的隶属度、非隶属度、犹豫度。Ai={〈x,μAi(x),νAi(x)〉|x∈X},A1⊂A2(i=1,2),当且仅当μA1(x)≤μA2(x),νA1(x)≥νA2(x)(∀x∈X)。
定义2[9-10]设Ωi⊆F(U)(1≤i≤m)是m维的模糊子集,如果T是FDT,则满足以下条件:
(1)T的节点属于F(U);
(2) 记F(U)由所有子节点构成,若有非叶子节点N,则存在i(1≤i≤m),满足Γ=Ωi∩N;
(3)T的每一个叶子节点对应一个或多个决策分类属性值。
其中,Ωi为分裂属性的分裂子集,Ωi中的元素是分裂属性中的取值。
定义3[10]假设Pi(i=1,2,…,n)是属性Ai的模糊分裂,且有fs∈Pi(s=1,2,…,l)表示属性Ai模糊分裂后的取值,则定义以下集合:
B≡Pi1∧Pi2…∧Pik(i=1,2,…,N;k=1,2,…,n)
(1)
通过上面的定义,可以计算模糊频率:
P(Ai1isf1|Ai2isf2∧…∧Aikisfk)=
(2)
定义4[11]设A是X上的模糊集,{μ1,…,μn},μi>μi+1为A的隶属度,A的质量分配函数mA的概率分布为
mA(Fi)=μi-μi+1
mA(F1)=1-μ2
(3)
其中,Fi={x∈Ω|μ(x)≥μi},i=1,…,n;集合F1,…,Fn是mA的焦点元素。

mA(Gi)=yi-yi+1,i=1,…,n-1
mA(Gn)=yn,mA(G1)=1-y2
其中,
Gi={x∈Ω|p(x)≥pi}
(4)

(5)
由于μ2+ν2+π2=1 ,所以有:
(6)
3 一种新的加权毕达哥拉斯模糊熵
在文献[14]中,作者定义的某些毕达哥拉斯模糊熵没有考虑犹豫度,所以当模糊性和犹豫性都最大时取到最大值。当μ=ν时,模糊度最大,这使得毕达哥拉斯熵值与模糊集定义的熵有矛盾,这是因为毕达哥拉斯模糊集的熵值受到模糊性和犹豫性的影响,当模糊性越大时,熵越大;犹豫性越大时,熵也越大。针对这种情况,对文献[14]定义做以下修改:即当μ=ν=0时,熵值取最大,此时模糊性和犹豫性都最大,所以能使熵值最大。接下来在考虑犹豫性和模糊性的基础上,对犹豫度和模糊度赋予权重,定义新的加权Pythagorean模糊熵。
定义7A是X上的PFS,A的模糊度为hA(x)=1-|μA2(x)-vA2(x)|,其中hA(x)∈[0,1]。
定义8 设A和B是X上的PFS,有以下条件:
(1)A为清晰集,等价于E(A)=0;
(2) ∀xi∈X,μA(xi)=νA(xi)=0,等价于E(A)=1;
(3)E(A)=E(Ac);
(4)E(A)是关于模糊度hA(x)的单调增函数,是关于犹豫度πA(x)的单调增函数。
若E满足以上条件,称E为PFS上的毕达哥拉斯模熵。
条件(4)的说明:当πA(x)=πB(x)且hA(x)≤hB(x)时,E(A)≤E(B);当hA(x)=hB(x)且πA(x)≤πB(x)时,E(A)≤E(B)。
定义9 设论域X={x1,x2,x3,…,xn},A是X上的PFS,定义新的加权Pythagorean模糊熵如下:
(7)
其中,ω1+ω2=1,0≤ω1≤1,0≤ω2≤1。
证明
1)E(A)=0⟺∀xi∈X,ω1fA(xi)+ω2πA(xi)=0⟺
∀xi∈X,ω1(1-|μA2(x)-vA2(x)|)+
0≤|μA2(x)-vA2(x)|≤1且0≤μA2(x)+vA2(x)≤1⟺∀xi∈X,|μA2(x)-vA2(x)|=1且μA2(x)+vA2(x)=1⟺∀xi∈X,uA(xi)=0,vA(xi)=1且uA(xi)=1,vA(xi)=0⟺A∈P(X)。
2)E(A)=1⟺∀xi∈X,ω1fA(xi)+ω2πA(xi)=1⟺
∀xi∈X,ω1(1-|μA2(x)-vA2(x)|)+
∀xi∈X,1-|μA2(x)-vA2(x)|=1

μA2(x)+vA2(x)=0⟺∀xi∈X,uA(xi)=vA(xi)=0

新的加权毕达哥拉斯模糊熵对模糊性和犹豫性赋予权重,符合毕达哥拉斯模糊熵的条件,同时考虑了模糊度和犹豫度对新的加权毕达哥拉斯模糊熵所起的作用,所以更符合客观实际。
4 WPFDT的生成过程
4.1 属性的模糊化
对于属性的模糊处理主要有两种,如果是清晰属性,则直接根据语言术语语义将隶属度标记为0或者1;如果是连续属性,则首先需要通过使用改进的K-means算法[14]求出各属性的聚类中心,得出各属性中心点就是三角隶属度函数的参数,从而将属性划分为对应数量的模糊集,然后用相应的模糊语言术语来描述连续值属性,最后使用上述所得的三角隶属度函数把数据转换成模糊数据。
4.2 分裂属性的选择标准
以属性A为例计算新的加权毕达哥拉斯模糊熵的过程如下:假设属性A有l个模糊子集As(s=1,…,l),两个决策属性C+和C-,则由式(1)得:
C+:w(C+∧As),C-:w(C-∧As),s=1,…,l
由式(2)计算每一个子节点As的相对频率:
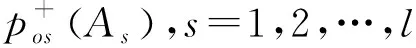
通过上述,计算所有条件属性的新的加权毕达哥拉斯模糊熵,选择熵最小的属性为决策树的根节点,递归地计算加权毕达哥拉斯模糊熵,从而选择分裂节点。
4.3 WPFDT的剪枝处理
WPFDT在生成过程中需要限制树的深度,如果生成的WPFDT深度太深,就会增加复杂的计算量,而且不一定有好的分类效果,因此要限制WPFDT的生长。在FDT中常用的限制树规模的方法有预剪枝、后剪枝等,都通过控制显著水平、真实度来控制树的规模,显著水平α和真实度β的定义见参考文献[15]。对于WPFDT的每一个待分裂节点都可以知道其隶属度、非隶属度,通过比较μA(x)、νA(x)与设定阈值的大小来决定是否对节点进行分割;设定的阈值为0.96(一般β0>0.75)[9],当μA(x)、νA(x)有一个值大于阈值时,则停止对该节点进行分割,当μA(x)、νA(x)都小于阈值时,则继续对该节点进行分割。
4.4 模糊规则抽取和分类预测
生成的WPFDT转换成模糊规则的过程如下:如果有n个叶子节点就会有n条模糊分类规则,n个模糊规则,WPFDT在抽取规则时不仅会得出叶子节点的分类结果,也会得出属于不同决策属性的μ、ν,同时也会得出模糊分类规则的犹豫度。WPFDT在预测过程中会有多个模糊规则可以适合匹配,选择所有隶属度中最大值的模糊规则结果作为预测结果,并得出规则的μ、ν、π。
5 WPFDT算法流程
步骤1 输入训练集,运用改进的K-means算法[14]和三角隶属度函数把数据转换成模糊数据。
步骤2 对于每一个Ai的每一个模糊子集值Aij(1≤i≤n;1≤j≤ki),根据式(1)和式(2)计算Aij相对于C+或C-的模糊频率pij。

步骤4 根据式(6)得每个子节点Aij由以下毕达哥拉斯模糊集描述:{Aij,μ(Aij),υ(Aij),π(Aij)}。
步骤5 根据式(7)计算每一个属性Ai的加权毕达哥拉斯模糊熵E(Ai),选取最小的E(Ai)作为根节点。
步骤6 设定阈值β0,当每个子节点μ(Aij)、ν(Aij)都小于β0时,继续对该节点Ai划分,否则标记成为叶子节点。
步骤7 在根节点下递归选取最小的加权毕达哥拉斯模糊熵对应的属性作为分裂节点,直至最终生成WPFDT模型。
6 WPFDT实例分析
假设有A和B两个条件属性,决策属性为C,其中A和B分别有两个条件属性A1,A2和B1,B2,C有C+和C-两个决策属性,假设有4个样本隶属度数据如下:μ(A1)=(1,1,0.59,0.01),μ(A2)=(0,0,0.41,0.99),μ(B1)=(1,0,1,0.88),μ(B2)=(0,1,0,0.12),μ(C1)=(0,1,0,1),μ(C2)=(1,0,1,0)。

接下来在属性B1的条件下计算模糊子集A1、A2的新的加权Pythagorean模糊熵。按照上面步骤,计算A1、A2分别相对于B1的相对频率,用式(4)和式(5)计算属性A在B1这个条件属性下支持C+的最大可能性。由式(7)可得μ(A1)=0,ν(A1)=0.98,π(A1)=0.199;μ(A2)=0.59,ν(A2)=0,π(A2)=0.807,由于只有两个属性,所以直接确定叶子节点,最终生成的WPFDT如图1所示。
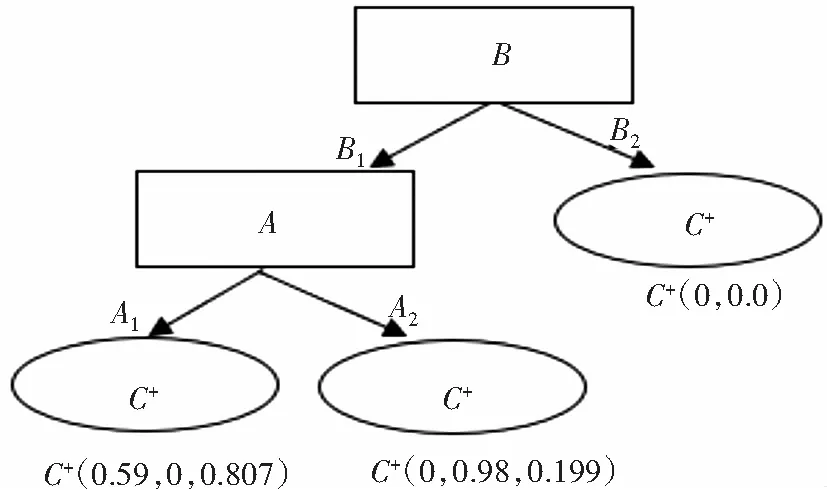
图1 加权毕达哥拉斯模糊决策树Fig.1 Weighted Pythagorean fuzzy decision tree
由图1可知,规则1:如果B是B1并且A是A1,则分类为C+,规则的μ、ν、π分别为0.59、0、0.807。规则2:如果B是B1并且A是A2,则分类为C-,规则的μ、ν、π分别为0、0.98、0.199。规则3:如果B是B2,则分类为C+,规则的μ、ν、π分别为1、1、0。
接下来用μ(A1)=0.37,μ(A2)=0.63,μ(B1)=1,μ(B2)=0进行预测。与规则1适合的隶属度min{1.00,0.63}=0.63,该样本属于C+类的可能性为0.59,属于C-类的可能性为0,犹豫度为0.807。与规则2适合的隶属度为min{1.00,0.37}=0.37,该样本属于C+类的可能性为0,属于C-类的可能性为0.98,犹豫度为0.199。与规则3适合的隶属度为min{0.00}=0,表示该样本属于C+类的可能性为1,属于C-类的可能性为0,犹豫度为0。最终选择与所有规则适合最高的条件隶属度结果作为分类结果,即选择规则1,分类为C+。
7 WPFDT实验分析
7.1 分类准确率对比
为进一步说明加权毕达哥拉斯模糊决策树的优越性,选取UCI上的Haberman、 Breast Cancer、Parkinson 3个医学数据集,将其与3种传统决策树算法(CART算法、C4.5算法、模糊ID3算法)进行实验比较,得到的分类准确率如表1,并得出WPFDT算法 的准确率、精确率、召回率、F1值如表2所示。

表1 分类准确率的对比

表2 WPFDT算法评价指标
由表1可知:本文的WPFDT算法在3个医学数据集上,分类准确率是最高的,表明对分裂节点过程中获取的模糊信息越全面,分类准确率越高。由表2知:WPFDT算法在较高的分类准确率情况下,有较高的召回率和精确率。
7.2 规则数量比较
叶子节点的数量越多,抽取规则的数量就越多,在分类预测时匹配规则就越多,得出的模糊决策树规模就越大,分类的准确性也越高,但当规则数量过多的时候,不仅带来过多的复杂计算,而且容易出现过拟合。下面比较4种算法在3个医学数据集(Haberman、Breast Cancer、Parkinson)上得出模糊规则的数量,得到的结果如表3所示。

表3 IF THEN规则的数量Table 3 Number of IF THEN rules
由表3可知:在Haberman、 Breast Cancer、Parkinson 3个医学数据集上,本文的WPFDT算法得出的规则数更加适中,说明生成的模糊决策树更容易理解,用较合适的规则就能进行更好地分类预测,分类性能更好。
8 结论与展望
提出一种新的加权毕达哥拉斯模糊决策树算法(WPFDT)。首先,使用改进的K-means聚类算法得到连续属性聚类中心,并结合三角模糊数对连续数据进行模糊处理;其次,定义并计算每一个属性的加权毕达哥拉斯模糊熵,选择加权毕达哥拉斯模糊熵最小的属性作为决策树根节点,在根节点下递归选择模糊熵最小的属性作为分裂节点,直至生成WPFDT模型,同时通过阈值控制树的规模,得到从根节点到叶子节点路径的模糊规则以及模糊规则的μ、ν、π,并完成预测分类;最后,将UCI上的数据集与3种传统决策树算法进行实验比较,结果表明:WPFDT在分类精度和树大小方面都优于其他决策树。在进一步工作中,将结合卷积神经网络[16],模糊逻辑优化加权毕达哥拉斯模糊熵,生成具有更优分类性能的模糊决策树。

