基于多维度跨尺度LSTM模型的时序预测

胡晓彤，程 晨

(天津科技大学 人工智能学院，天津 300457)

0 引 言

金融时间序列数据通常伴随着大量的噪声，呈现出非线性、非平稳性等复杂特征[1,2]，导致金融时间序列数据很难预测准确。根据时间序列数据的内在变化规律，主要归类为线性预测和非线性预测两种方法[3,4]。

在线性预测中常用的经典方法一般是指数平滑方法、自回归积分移动平均方法等，该类方法结构简单，计算量少，可以对短期数据进行预测，但是面对长期数据存在局限性。非线性预测方法包括BP神经网络[5]、支持向量机、循环神经网络[6]等，非线性预测方法能全面描绘出金融时间序列数据之间的非线性联系，并能取得相对准确的预测数据。

本研究采用的是非线性预测方法中的循环神经网络模型方法，即递归神经网络(recurrent neural network，RNN)。由于RNN模型训练时容易陷入梯度消失问题，于是出现了长短期记忆神经网络模块(long-term and short-term memory network，LSTM)，LSTM模型是一种改进的时间循环神经网络，它解决了RNN模型存在的梯度消失问题。但是LSTM模型在进行长期金融时间序列数据预测时是依然存在滞后性问题[7]，即时间序列预测中预测数据相较于真实数据滞后的问题，一般都是信息不足而导致预测的滞后。针对这种滞后性问题，本文将通过在LSTM模型加入最值选择模块和预测过程中实现短周期数据转化为长周期数据方法，来降低预测数据的滞后性。

为了提高预测数据精度的，有从数据角度的出发，如基于多源异构数据的结合与处理等[8-11]提升模型的预测精度，也有从模型结构的改变[12,13]提升预测精度。本研究在跨尺度LSTM预测模型基础上，通过结合经济学技术性指标多维度数据输入，来提高模型预测精度。实验过程中还发现，依据k线图思路，对金融序列数据进行差值法处理后输入训练，模型的预测精度更高，滞后性更弱。

1 LSTM结构及原理

LSTM网络结构(如图1所示)是由多个小型神经网络循环连接构成。这些小型神经网络结构是由一个或多个细胞(cell)自连接组成，为实现小型神经网络结构具有记忆功能，故在网络结构还添加了遗忘门(forget gate)、输入门(input gate)和输出门(output gate)3种门限单元系统，所以这些小型神经网络也称为记忆模块。

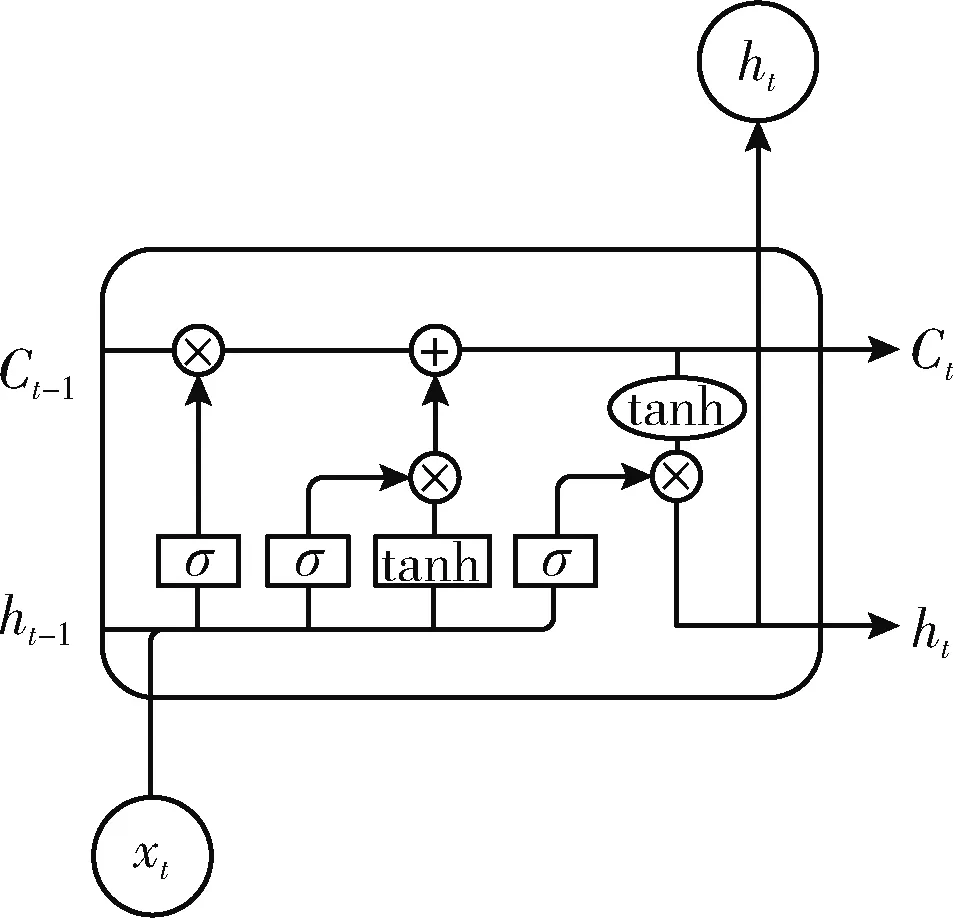
图1 LSTM网络单元

其中，LSTM网络结构中数据处理流程如下：

先是经过遗忘门ft从细胞中保留所需要的信息

ft=σ(bf+Wfxt+Ufht-1)

(1)

式中：σ为sigmoid激活函数。xt即t时刻的输入向量，ht-1即t-1时刻的隐藏层向量，bf为偏置循环权重，Wf为输入权重，Uf为遗忘门权重。

接着，重置细胞中的信息。gt由sigmoid激活函数控制0-1之间的输出门

gt=σ(bg+Wgxt+Ught-1)

(2)

则在Ct-1基础上更新细胞状态Ct为

Ct=f*Ct-1+gt*tanh(bc+Wcxt+Ucht-1)

(3)

最后，由输出门ot控制信息输出

ht=ot*tanh(Ct)

(4)

其中，输出门

ot=σ(bo+Woxt+Uoht-1)

(5)

通过上述操作，LSTM模型就能高效利用输入历史数据，从而具有记忆功能。

2 跨尺度预测方法

为解决LSTM模型预测滞后性问题，这里提出一种跨尺度预测方法，即用短周期数据训练模型，预测长周期数据。对于同一时间跨度的金融序列数据，短周期的数据量是大于长周期数据量的，比如周期2H的数据量是周期6H的数据量的3倍，即1个长周期时间点需要3个短周期时间点来表示。短周期的数据变化率相较于长周期的数据变化率将更小，且金融数据趋势波动反馈快，那么通过短周期数据集训练的模型进行预测，将其预测的短周期数据转化为长周期数据，从而达到降低预测长周期数据的滞后性。

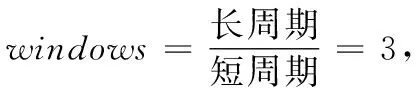
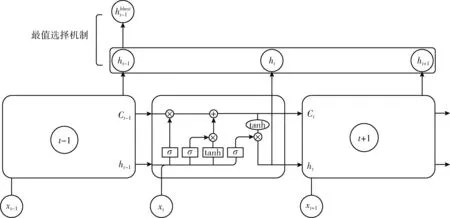
图2 跨尺度LSTM网络结构

3 跨尺度多维度预测方法

3.1 结合经济学技术性指标数据

金融经济学发展到现在，已经有很多完善的经济参数技术性分析指标。金融市场交易员依据技术性指标可以预测市场变动。一些常用的技术指标包括：相对强弱指数(relative strength index)、资金流向指数(money flow index)、离散指标(stochastics)、平滑异动移动平均线(MACD)和布林带(Bollinger Bands)。本研究选取布林带与MACD技术性分析指标作为研究，观察这些技术性指标数据的加入对模型预测精度的影响。

布林带技术指标类似轨道线指标，能反映金融数据波动趋势范围。

布林带有3条线形成。中间线为一般移动平均线(RollingMean)

(6)

高轨道线(BollingerHigh)

(7)

低轨道线(BollingerLow)

(8)

其中，SMA为t周期简单移动平均，D为特定标准偏差数。

这里关于布林带参数的设定选择，多次实验经验得出，本研究当t选取20，D为1.7时，模型预测效果最优。

MACD也称为移动平均聚散指标。MACD指标是通过利用快速(短期)和慢速(长期)移动平均线，还有两种平均线的聚合与分离征兆，进行双重平滑运算而得到。MACD指标是基于移动平均线原理发展而来的，具有两个优点，一是去除了移动平均线频繁发出虚假信号的缺陷，二是保存了移动平均线的效果，所以，MACD指标具有均线稳定性、趋势性、安定性等特征，一直以来被从事金融市场人员用来预测金融市场的涨跌。

首先计算平滑系数，其中n为周期数，本研究周短期n=12，长期n=26

(9)

计算指数平均值(EMA)

(10)

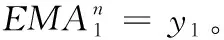
计算出离差值(DIF)

(11)

计算出平滑移动平均线DEA

DEAi=(8*DEAi-1+2*DIFi)/10, (i>1)

(12)

其中，DEA1=DIF1。

计算MACD

MACDi=2*(DIFi-DEAi)

(13)

经过数据处理，得到的多维度数据格式部分截图如图3所示。基于跨尺度预测方法的基础上，将多维度数据作为输入向量进行训练。

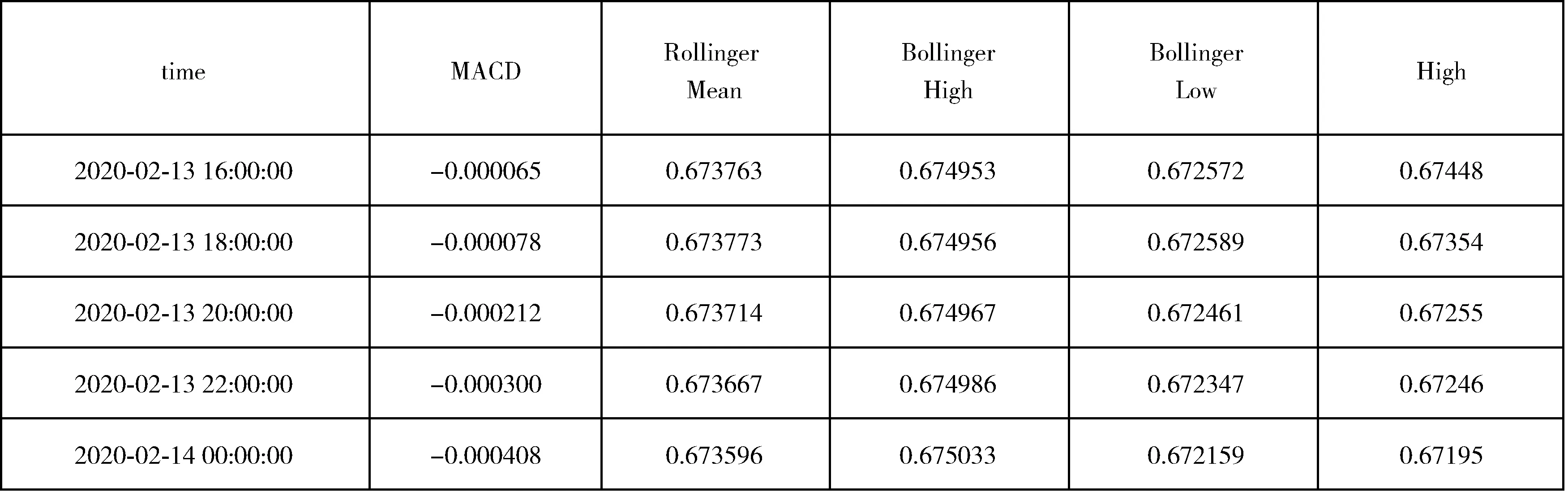
图3 多维度数据集格式

3.2 改进型多维度跨尺度预测方法

金融市场常用的K线图(俗称蜡烛图，如图4所示)来描绘金融市场曲线，K线图相较于金融时序数值数据的优势，在于K线图中蜡烛线能够分割为不同的时段进行使用，各种周期的时序数据适合。另一方面，K线图是由一定时间段的金融时间序列数据的open、close、high和low组成，所以K线图能够更好地表示金融市场的价格波动趋势及规律[14]。

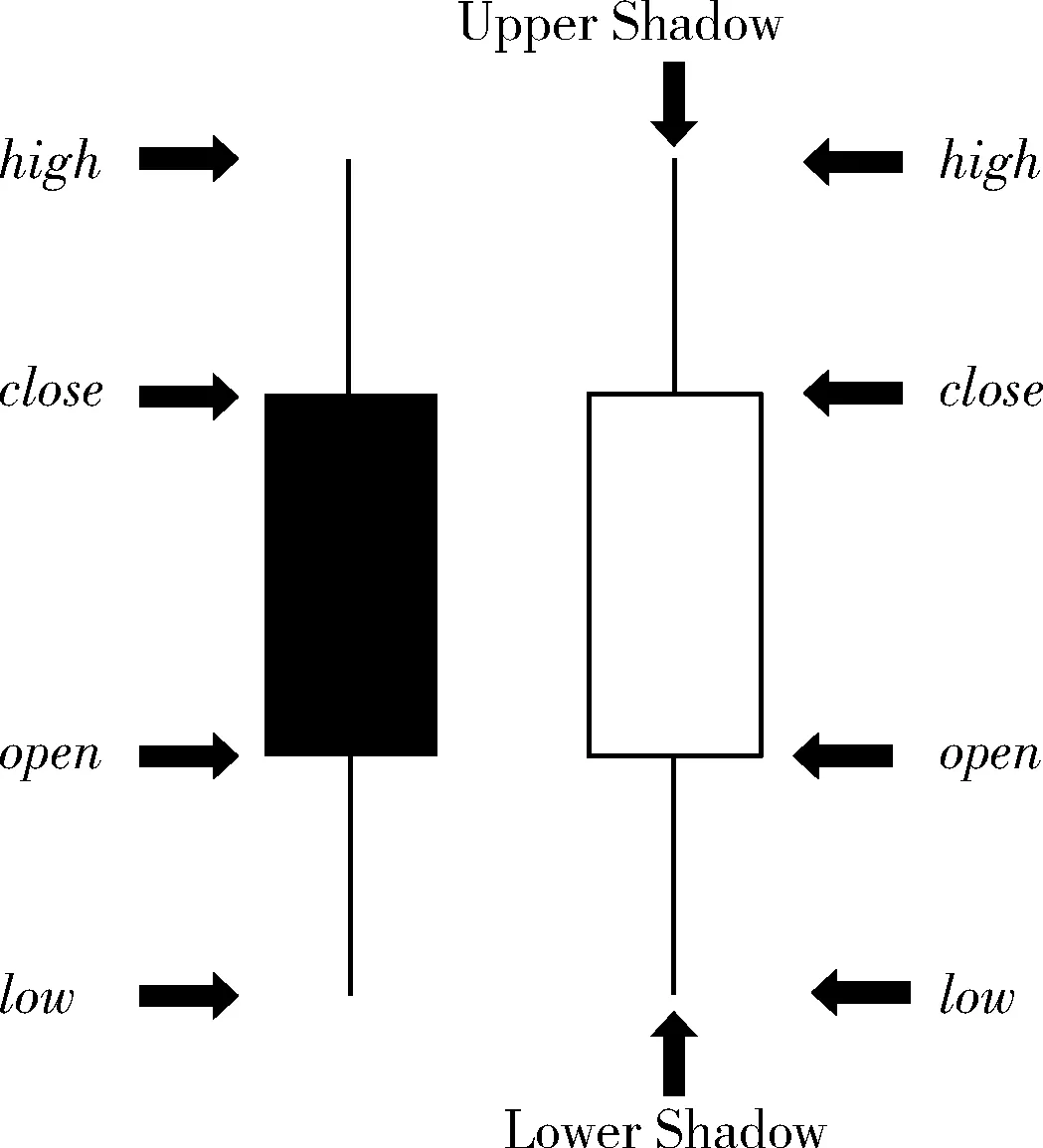
图4 K线图

通过时序数据数值变化来提取K线图所表示的数据变化信息及规则，这里采用差值法来提取K线图的特征信息。也就是将各个时间点的最高值与前一个时间点的闭盘价的差值，作为模型的输入输出向量对象进行训练。

具体方法步骤：

步骤1 首先进行数据处理，针对每个时间点，将第t+1 时间点的hight+1值与第t时间点的closet值进行相减，即xt+1=hight+1-closet，xt+1表示第t时间点闭盘价与第t+1时间点最高值的差值。

步骤2 同理，将第t时间点的hight值与lowt值进行相减，即yt=hight-lowt，yt表示第t时间点的最高值与最低值的差值。

步骤3 将第t时间点xt，yt， 布林带数据和MACD数据组成新的数据格式，对每个时间点数据进行相同地处理，得到的数据集其特征数为6个维度，部分数据集格式如图5所示。然后将新的数据集放入跨尺度多元LSTM模型中进行训练。训练过程中，模型的窗口序列长度设置为20个。

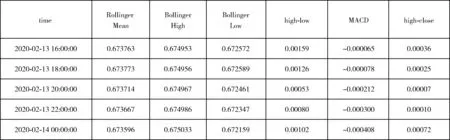
图5 数据集格式

步骤4 该跨尺度LSTM模型设置为二元预测输出，以预测第t+1时间点为例，该模型输出的预测值分别为第t+1时间点的xt+1和yt+1。 根据第t时间点的实际closet值，就可以预测出第t+1时间 点的最高值hight+1=closet+xt+1， 和最低值lowt+1=hight+1-yt+1。

4 实验流程及验证分析

4.1 数据采集及预处理

这里金融序列数据采用外汇数据集，数据来源于软件MetaTrader5。通过Python中MetaTrader5库获取数据进行数据分析处理。

该实验数据采用H2短周期数据进行训练模型，来预测H6周期金融数据价格。

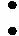
由于多维度向量数据实验中，需要结合布林带和MACD等指标数据输入，这与外汇数据集的取值范围差异化太大，防止数值差异对模型训练结果影响过大，必须进行归一化处理，这里将数据集的数值控制在0-1范围内。归一化公式如下

(14)

式中：x为原数据集数值，y为处理后的数据集数值，MaxValue为数据集中的最高值，MinValue为数据集中的最低值。

4.2 模型搭建

经过多次调参及优化，本研究发现，将模型的测试窗口序列长度设置为20，模型的网络结构包含2层LSTM层，其中的神经元个数均设置为128。还在网络结构中增加2层Dropout层，其中dropout系数设置为0.1，再加入1层Dense层，激活函数为relu，再加入1层Dense层，激活函数为linear，得到的最终模型结构如图6所示。模型的损失函数这里设置为均方误差(mean squared error，MSE)，优化算法设置为Adam。对模型进行训练300个Epoch，每个Batch设置为256。

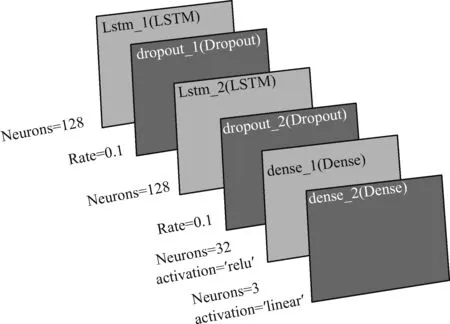
图6 LSTM模型层次结构

模型参数设置的详细见表1。

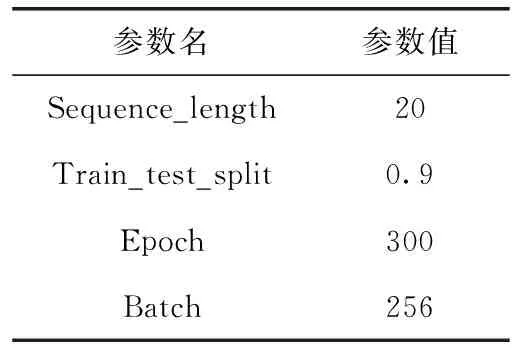
表1 模型参数设置

4.3 模型评价指标

为了评价模型的预测能力，这里采用均方误差MSE作为评价指标

(15)

其中，n为预测点的总个数，yi为真实值，y′i为对应点预测值。

针对模型的预测滞后性评价，本研究采用的是方红等[7]实验中使用的评价指标，即预测滞后性lag

(16)

其中，M、N分别表示测试集预测值和真实值数列内的极大值与极小值的数量和，ti和tk分别表示测试集预测值和真实值数列第i和k各极值对应的排序值。lag越小，说明滞后性越小。

4.4 实验结果与分析

实验一：跨尺度单元LSTM模型与单元LSTM模型预测效果对比。

为验证跨周期尺度预测金融数据方法的效果，这里选取外汇数据中的最高值(high)作为输入对象进行训练。这里LSTM模型设置为单元输入LSTM模型。这里跨尺度单元LSTM模型与单元LSTM模型结构参数相同。

验证集为300条周期2H数据。跨尺度单元模型输出预测最高值数据300条，将其转化为100条周期6H的数据，即3个连续时间点的周期2H的数据中选择最大值作为周期6H的时间点预测值。相对的，周期6H单元LSTM模型输出预测最高值数据100条。实验结果如图7所示。

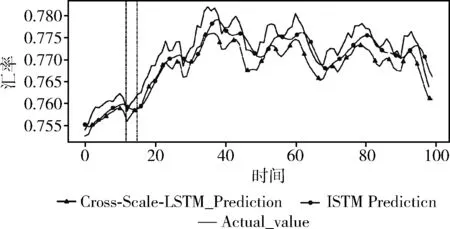
图7 跨尺度单元LSTM模型与单元LSTM模型预测效果对比

图7中，实心曲线为实际周期6H的金融数据曲线，圆点曲线为周期6H单元LSTM模型预测最高值数据曲线，三角点曲线为短周期2H预测长周期的跨尺度单元LSTM模型预测最高值数据曲线。

这里采用MSE和预测滞后性评价指标来进行分析评价，其中Train_MSE为训练集均方误差，Test_MSE为验证集均方误差。结果见表2。

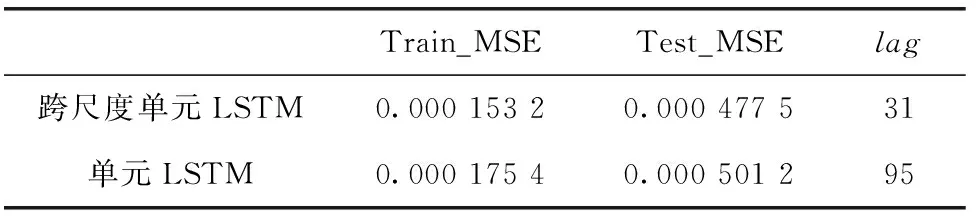
表2 跨尺度单元LSTM模型与单元LSTM模型预测结果

从结果上看，短周期预测长周期跨尺度LSTM模型相较于传统同周期预测LSTM模型，在预测金融数据更具有优势，跨尺度单元LSTM模型均方误差为0.000 153 2低于单元LSTM模型的0.000 175 4，可以看出跨尺度单元LSTM模型预测的准确度较高。

本实验中短周期预测长周期跨尺度单元LSTM模型预测结果，其滞后性指标lag=31远低于同周期预测单元LSTM模型lag=95，从图中也可看出本周期6H单元LSTM模型预测值曲线与真实值曲线明显存在“延后平移”，以图7中时间点10～20段为例，实际数据的极小值位置与跨尺度单元LSTM模型预测数据极小值位置一致(即第一个虚线标注位置)，而对应的单元LSTM模型预测数据极小值位置在下一个虚线位置。说明跨尺度单元LSTM模型预测值曲线更符合实际曲线的趋势波动，表明短周期预测长周期方法能减弱金融时间序列数据预测的滞后性。

实验二：结合技术性指标数据多维度跨尺度LSTM模型预测效果对比。

在跨尺度LSTM模型的基础上，这里通过加入技术性指标布林带数据、MACD数据，来观察该多维度跨尺度LSTM模型的预测效果。实验为3组，分别为结合布林带数据、结合MACD数据和同时结合布林带与MACD数据。

这里将跨尺度模型设置为多元输入，模型分别预测了最高值和最低值，为了更加清晰地显示出模型预测效果，这里结合K线图进行展示。图中实心曲线为预测的最高值，实心三角曲线为预测的最低值，图中K线图表示的是实际金融数据波动范围。

实验结果如图8～图10。

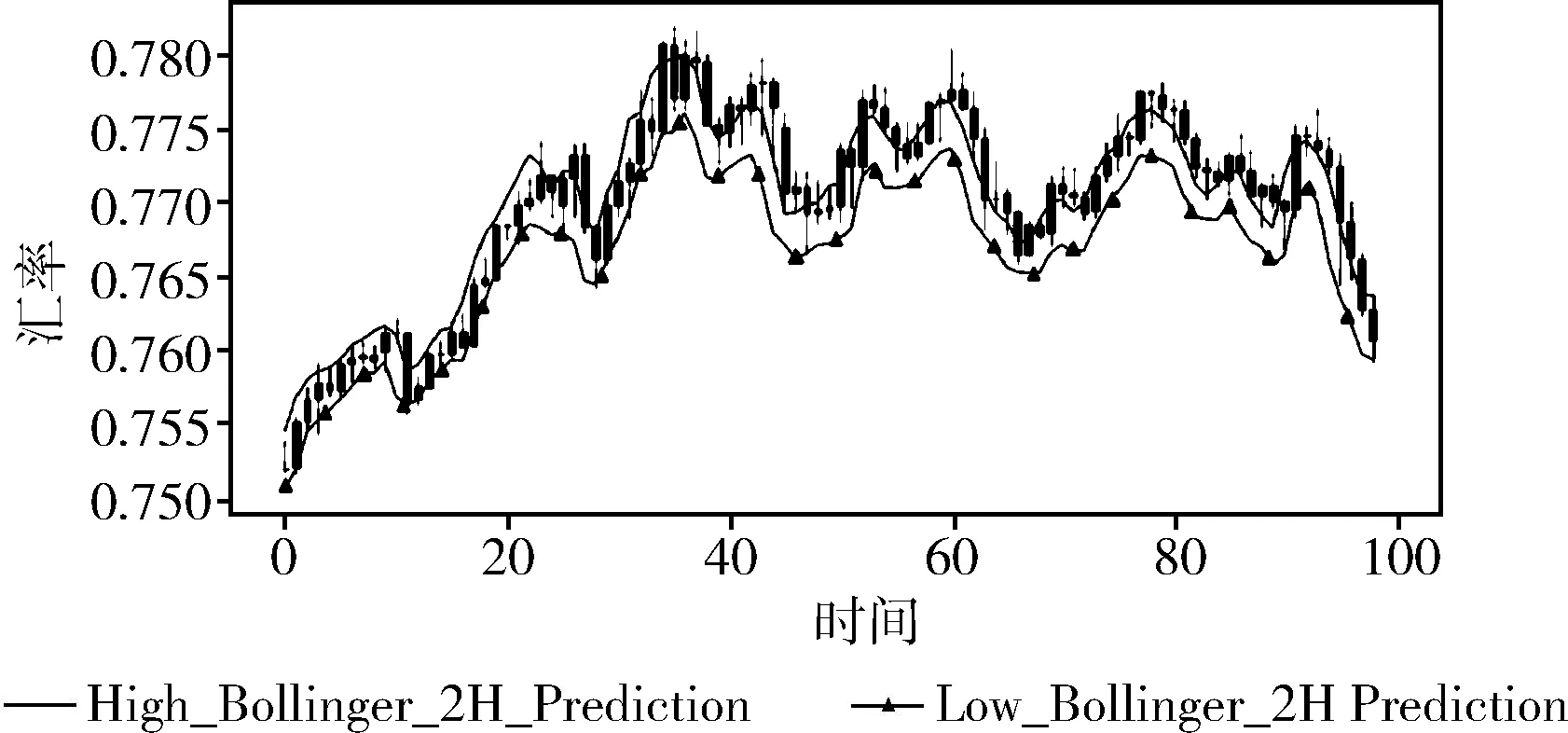
图8 结合布林带数据多维度跨尺度LSTM模型预测结果

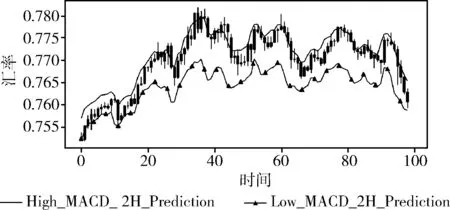
图9 结合MACD数据多维度跨尺度LSTM模型预测结果

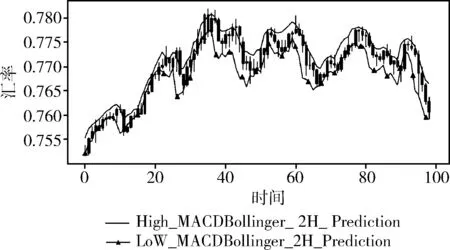
图10 结合布林带和MACD数据多维度跨尺度LSTM模型预测结果

采用MSE和预测滞后性评价指标来进行分析评价，其中Train_MSE为训练集均方误差，Test_MSE为验证集均方误差。结果见表3。

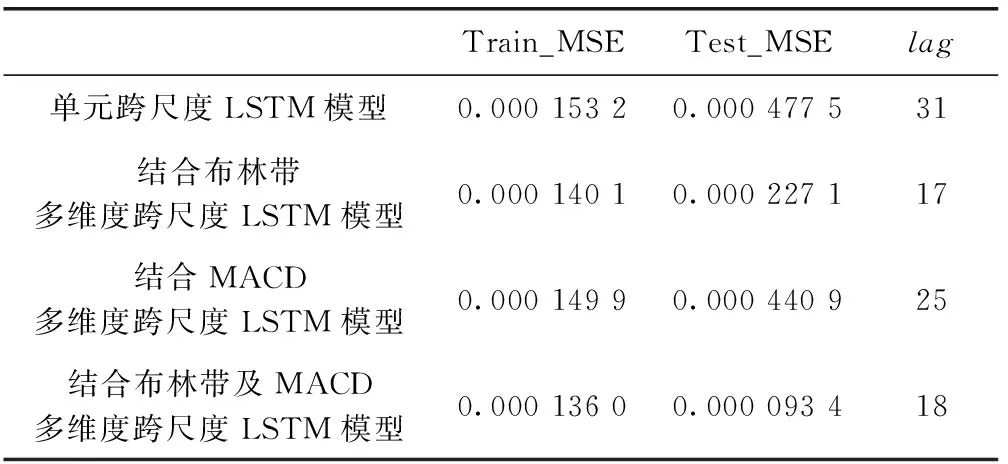
表3 结合不同数据集多维度跨尺度LSTM模型预测结果

从实验结果中，可以看出相较于单元跨尺度LSTM模型的预测结果，结合技术性指标数据的多维度跨尺度LSTM模型的预测精度更高，均方误差均小于单元跨尺度LSTM模型，但滞后性没有太大的变化。结合布林带数据的多维度跨尺度LSTM模型的均方误差相较于结合MACD数据的减少了0.000 009 8，可以看出布林带数据对金融数据预测的效果更优。

结合经济学技术性指标数据的多维度跨尺度预测方法提高了模型的预测精度。

实验三：改进型多维度跨尺度LSTM模型预测效果对比。

在实验二的基础上，即效果最优的结合布林带和MACD多维度跨尺度LSTM模型的基础上，观察依据K线图思路的改进型多维度跨尺度数据预测方法的效果。实验结果如图11所示。

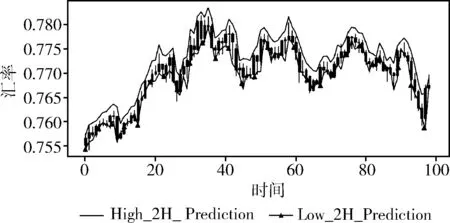
图11 改进型多维度跨尺度LSTM模型预测结果

采用MSE和预测滞后性评价指标来进行分析评价，其中Train_MSE为训练集均方误差，Test_MSE为验证集均方误差。结果见表4。

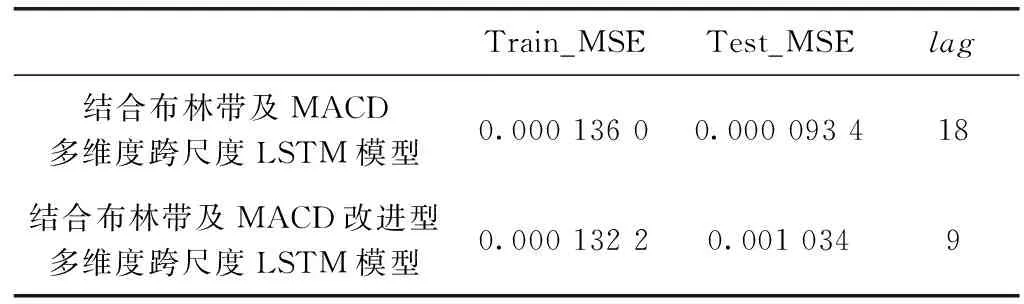
表4 改进型多维度跨尺度LSTM模型预测结果对比

从图11和图10的实验结果看，依据K线图思路的改进型多维度跨尺度LSTM模型预测方法的预测结果中，预测的最高值和最低值将实际金融数据K线图所显示的波动范围完全包裹，更好地拟合了金融数据的波动趋势。从实验评价指标看，改进型多维度跨尺度LSTM模型的训练和测试均方误差均低于多维度跨尺度LSTM模型，说明改进性多维度跨尺度LSTM模型预测精度更高，且预测滞后性为9也低于多维度跨尺度LSTM模型。

5 结束语

本研究为了解决LSTM模型对金融时间序列数据预测时存在的滞后性问题，提出一种跨尺度LSTM模型，通过短周期数据预测长周期数据方法，减弱了LSTM模型对金融时序数据预测的滞后性。并在此基础上，结合经济学技术性指标数据进行多维度跨尺度预测，提高了模型预测精度。

不同于传统金融数据预测方法，直接将金融时序数据(如最高值或最低值)放入模型中进行训练来预测未来金融数据变化。本研究根据金融市场K线图理论，对金融时序数据进行处理，通过时序数据数值变化来描述K线图所表达的数据变化信息及规律，基于改进型多维度跨尺度LSTM模型对该处理后的时序数据进行训练预测，实验结果表明，该预测方法相较于传统预测方法，预测精度更高，滞后性更低。因此，这种改进型多维度跨尺度LSTM模型预测方法在实际应用中可以发挥重要作用。