有关线图两个性质的讨论

孙林，蔡华，杨红梅

(1.山东大学 数学学院，山东 济南 250000；2.昌吉学院 数学系，新疆 昌吉 831100)

有关线图两个性质的讨论

孙林1,2，蔡华1,2，杨红梅2

(1.山东大学 数学学院，山东 济南 250000；2.昌吉学院 数学系，新疆 昌吉 831100)

通过介绍线图的内部结构，对线图的连通性以及线图是否为自补图的问题进行了详细的讨论，并得出一些结果.

线图；K1,3；边连通度；强连通；自补图①

1 引言

线图的概念是由Harary 和Normal 于1960年首先提出来的.它是从一个已知图构造另一个图的重要方法.线图中的许多图论性质，比如顶点度，连通性，同构等都可以很方便地从原始图导出来.线图是从图中与边有关的性质导出与顶点有关的性质的重要工具.文中主要用到以下基本概念和性质.

设G是一个图,分别用V(G)和E(G)表示图G的顶点集和边集，用dG(x)表示顶点x在G中的度数，N(x)表示顶点x的邻点集. 设G=(V,E)是无孤立点的无向图，G的线图记为L(G)，L(G)的顶点集为E(G)，L(G)中顶点e1,e2相邻当且仅当它们在G中相邻.如果在G中存在Φ≠B⊆E(G)，使得G-B中的连通分支数大于G中的连通分支数，则称B为G中的边割集，λG为G中所有边割集的最小边数.设G=(V,E)是无孤立点的有向图(可以有环和平行边)，G的线图记为L(G)，L(G)的顶点集为E(G)，L(G)中顶点a,b相邻当且仅当在G中a的终点是b的起点.有向图的线图通常简称为有向线图.图G的禁用子图G′指的是：若图G存在，则此图不可能含有子图G′.文中所涉及到的图G均为无向简单图或有向简单图.未说明的记号和术语参见文献[1,2，3].

定理1.1[4]设G是无向图，L(G)是G的线图,则

(1)L(G)是简单图，有ν(L(G))=ε(G)

(2)e=xy∈E(G),有dL(G)(e)=dG(x)+dG(y)-2，因此δ(L(G))=ξ(G)

定理1.3[6]设G是无向图，λL≥2λG-2

记λL为线图L(G)的边连通度，δL为线图L(G)的最小度，即图G的最小边度.

2 线图的内部结构及相关定理

线图的特有结构基本是通过线图的禁用子图来体现，在文献[2]中线图的禁用子图已经给出，但是关于其证明，很少有相关文献研究，现就其中一种重要禁用子图K1,3给出简洁的证明方法.

定理2.1[2]任何线图都不含4阶导出子图K1,3.

证明：反证法，假设某线图L(G)含4阶导出子图K1,3，则K1,3应是由G的4条边导出子图H的线图.由引言的定理1.1(1)(3)分别可得，

ν(K1,3)=4,ε(K1,3)=3,ε(H)=4.

所以

①

由上式知，∀x∈V(H),dH(x)≤3，又知H是连通图，所以∀x∈V(H),1≤dH(x)≤3.

设H中有n1个1度顶点，n2个2度顶点，n3个3度顶点，则ν(H)=n1+n2+n3.

由①式得

n1+4n2+9n3=14

②

由握手定理得

n1+2n2+3n3=8

③

②-③得

n2+3n3=3,0≤ni,i∈{1,2,3}

所以

n2=0,n3=1或n2=3,n3=0

由①式得

n1=5,n2=0,n3=1或n1=2,n2=3,n3=0

由此产生两个度序列，分别为(1,1,1,1,1,3)或(1,1,2,2,2)，第一个度序列不可图示化，第二个度序列对应唯一一个图P4，但其线图不是K1,3.

由此这样的H不存在，所以任何线图都不含4阶导出子图K1,3.

由以上的定理，可以得到以下两个关于线图的结论：

结论一：在文献[5]中，给出了关于判定某图是否为线图的一个必要条件：

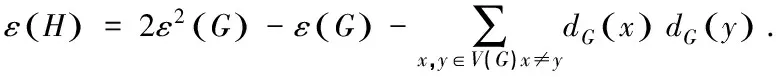
但是此结论反之则不成立.

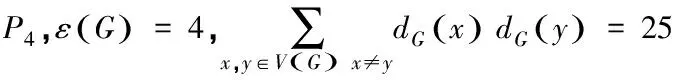
但由定理2.1.1知，K1,3不是P4的线图.

结论二：线图中任何顶点子集的导出子图是某个图的线图，但对于边导出子图，此论述不正确.线图L(G)中可以有边导出子图为K1,3，但由定理2.1.1知，此子图不是任何图的线图.

3 主要结论

3.1 线图的连通性

连通性是线图的重要性质，我们试图从原图当中推出其线图连通方面的结果.其中，易得λ(G)≥κ(L(G))不成立.由图1可看出，图G的最小边割集不一定是L(G)的最小点割集，如图1，图G的一个最小边割为{e1,e2,e3}，但{e1,e2,e3}不是L(G)的最小点割集.以下命题主要讨论原图的连通性质和其线图的连通性质的关系.

图1 原图的连通性质和其线图的连通性质的关系

命题3.1.1 设G=(V,E)是无孤立点的无向图，若λG≥3,则λL=2λG-1当且仅当G中存在两个相邻的顶点x和y使得dG(x)=λG且dG(y)=λG+1，且

e=xy∈E(G),ξ(G)=dL(e)=δL.

由定理1.2知，λL=δL，则存在e=xy∈E(G)且ξ(G)=dL(e)=δL，使得

2λG≤dG(x)+dG(y)=ξ(G)+2=δL+2=2λG+1.

另一方面，dG(x)≥λG,dG(y)≥λG

所以

dG(y)=λG,dG(x)=λG+1或dG(y)=λG+1,dG(x)=λG.

⟸ 已知x和y是G中两个相邻的顶点，且dG(x)=λG,dG(y)=λG+1，则

λL≤δL=ξ(G)=dG(x)+dG(y)-2=2λG-1

由定理1.3知，λL≥2λG-2，所以λL=2λG-2或λL=2λG-1.

假设λL=2λG-2，见必要性证明，同理可得λL=δL，所以

λL=δL=2λG-2≤2δG-2≤ξ(G)=δL

所以2δG-2=ξ(G)，这与e=xy∈E(G),ξ(G)=dL(e)=δL=2λG+1矛盾.所以λL=2λG-1.

命题3.1.2 设G=(V,E)是无孤立点的简单有向图，E′⊂E(G),|E′|≥2,L′是L(G)的子图使得E′=V(L′)，则如果L′是强连通，则G[E′]也是强连通的.

证明：由L′是强连通有向图，∀x,y∈V(G[E′])，则存在a,b∈E′，使得

a=(x,z),b=(y,u)∈E′.

因为L′是强连通 ，则a,b之间至少存在一条有向路，令W=(a,a1,a2,…,am,b)是L′中一条最短(a,b)路，这条路中的顶点，即G[E′]中的边构成一条(x,u)链，因此，G中有一条(x,y)路.由x,y∈V(G[E′])的任意性知，G[E′]也是强连通的.

3.2 线图的自补图的性质

线图的同构性质也可以在某些特殊情况下从原图中得到.如果T1,T2是两棵树，且L(T1)≅L(T2)，那么T1≅T2，但是对于任何图G不一定成立.例如，K3是K3和K1,3的线图，但K3与K1,3不同构.同时还有自补图的概念，即Gc是图G的补图，若G≅Gc，则称图G是自补图.以下讨论关于L(G)为自补图的一个充分条件.

命题3.2.1L(G)为k-正则图G(k≥1)的线图，且n=2k.若在G中有2k个完美匹配，且存在一个顶点x∈V(G)，满足

则L(G)为自补图.

证明：因为G中存在一个顶点x∈V(G)，有

则可将G中得边按如下排列：第一行为与x关联的k条边ee,e2,…,ek，设ee,e2,…,ek的不同于x的另一个端点为y1,y2,…,yk.

例L(K3,3)是自补的.

证明：设K3,3的两部分顶点集为V,V′，V={1,2,3},V′={1′,2′,3′} .

由K3,3的性质知，L(K3,3)是9个顶点的4-正则图，且L(K3,3)中的顶点由K3,3中其对应的边的两个顶点来表示，即V(L(K3,3))={11′,12′,13′,21′,22′,23′,31′,32′,33′}.

我们可以建立一双射φ，

φ(11′)=11′,φ(12′)=22′,φ(13′)=33′

φ(21′)=23′,φ(22′)=31′,φ(23′)=12′

φ(31′)=32′,φ(32′)=13′,φ(33′)=21′

从上述映射可以看出每一行的像集Gi与每一列的像集Hj分别是K3,3的匹配，i,,j∈{1,2,3}. 显然，此匹配映射φ保持L(K3,3)与其补图的邻接关系，所以L(K3,3)是自补的.

根据线图和原图的关系，当以L(G)为自补图时，可以根据这一特性，得出原图相应的性质，由此，以下讨论L(G)为自补图的必要条件.

所以

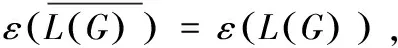
即

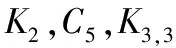
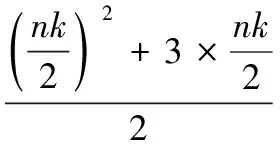
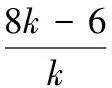
(2,1),(5,2),(6,3),(7,6)

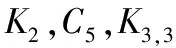
通过介绍线图的内部结构，对线图的连通性以及线图是否为自补图的问题进行了详细的讨论，并得出一些结果.但是，关于线图为自补图的充分必要条件还没有得出结果，希望在以后的研究中解决此类问题.

[1] Bondy J A,Murty USR. Graph Theory and Application[M]. NewYork: Academic press,1976：42-45.

[2] Douglas B.Introduction to Graph Theory[M].北京:机械工业出版社,2004:273- 282.

[3]殷剑宏,吴开亚.图论及其算法[M].合肥：中国科学技术大学出版社,2003:20-21.

[4]Lowell W.Beineke,Robin J.Wilson,Selected Topics in Graph Theory[M].NewYork, Academic press,1978：273-274.

[5]徐俊明.组合网络理论[M].北京：科学出版社,2007:40-41.

[6]Hellwig A, Rautenbach D, Volkmann L. Note on the connectivity of line graphs [J]. Inform Process Lett, 2004, 91(1): 7-10.

SomeTopicsonLineGraphs

SUN Lin1,2,CAI hua1,2,Yang Hong-mei2

(1.College of Mathematics,Shandong University,Jinan 250000,China;2.Department of Maths,Changji 831100,China)

In this paper, firstly, the structures of line graphs are discussed. Secondly, its connectivity and self-complementary property are stated, some results of which are given.

Line graphs; K1,3; edge connectivity; strong connectivity; self-complementary graph

O153.3

A

1004-7077(2013)05-0055-05

2013-09-02

孙林(1981-)，女，陕西汉中人，山东大学数学学院在读博士研究生，昌吉学院数学系讲师，主要从事图论及其应用的研究.

闫昕]