单层复合材料飞轮转子仿真计算分析

张兴蕾，李帅

(枣庄学院 机电工程学院，山东 枣庄 277160)

0 引言

利用高速旋转的飞轮进行能量存储是一种古老而又存在广泛前景的机械储能技术.飞轮能源储备装置具有储能大、效率高、寿命长、无污染、体积小等优点，越来越被各国所重视，在电网调峰、航空航天、不间断供电备用电源等领域都展开了广泛研究.复合材料飞轮处于高速旋转状态下，其离心应力不容忽视，本文通过ANSYS静力分析模块对高速旋转的复合材料飞轮转子进行应力仿真分析，并与理论计算结果进行比较，为以后复合材料飞轮转子的应力分析提供一定的参考依据.

1 复合材料有限元分析简介

匀速旋转实心圆盘的力学问题，弹性力学已经给出了精确的解析解，然而对于各向异性材料(复合材料飞轮转子)，却很难得到较为精确的解析解.在求解原理方面，复合材料有限元法其实是与各向同性材料相同的.本文是基于复合材料宏观有限元法上进行求解的，即将增强材料与基体复合后，再讨论其宏观的力学行为，所以在分析的求解过程中可以将复合材料的微观力学行为忽略掉.有限元法在复合材料的离散化上具有双重性特点，即沿表面的结构离散与沿厚度方向各铺层的离散.有限元分析的一般流程如图3－1所示［1］:

弹性力学与塑性力学在本质上的区别是:材料在塑性阶段，其应力应变曲线具有非线性的关系，在有限元的计算过程中，塑性区域内的应力是采用不同的本够关系进行求解的，然而，弹性区域内的材料其应力应变关系仍然是线性的，弹—塑性的交界区域由于在应力与位移连续性和变形协调条件上是不满足的.所以，针对较为复杂的力学问题，使用有限元法来分析是很有必要的.

运用有限元法求解弹塑性问题，本质上是将非线性的应力应变问题转化为线性关系的问题后再进行处理的，一般情况下采用的是增量类型理论，即将总的载荷分为若干个增量载荷，然后将其逐渐加载到结构上，最后通过变刚度法进行求解.

在有限元分析中，计算弹塑性问题的刚度矩阵表达式为:

弹性区域:

塑性区域:

在弹性区域与塑性区域的过渡区域:

2 复合材料强度准则与破坏准则

2.1 复合材料的强度准则

在复合材料飞轮转子缠绕角可以忽略的条件下将其看作为单项的复合材料，而单向复合材料的几种常用强度准则为:最大应变强度准则、最大应力准则、Tsai－Wu强度准则、Hoffman强度准则以及Tsai－Hill强度准则.

其中，Tsai－Wu强度准则，其表达式为:

其中，Fi和 Fij为材料强度的性能参数，可通过基本的强度 Xt，，，Xc，Yt，Yc，Zt，Zc，

S表达出来，由于飞轮转子为轴对称平面问题，表达式可写作:

2.2 破坏准则

机械零件结构设计和校核的重要依据是破坏准则，它的选取决于所选零件的材料.针对各向同性材料(如金属)，一般采用最大应力、最大应变准则.最大应力准则和最大应变准则的破坏条件是

式中的下标i，j代表正交坐标系下的3个方向.

该准则的最大优点是易于判断最大应变或者是最大强度否在材料许用的强度极限之内，在此基础上可以比较容易地判断出材料的破坏形式.而变形能量准则应用于其应力的分布不

属于平面应力状态的情况下，它的等效应力表达式为:

式中 σ1，σ2，σ3—— 正 轴应力.

然而，对于正交各向异性材料(复合材料)，主要有三种破坏准则:最大应力准则、最大应变准则以及形变应变能准则.其中，最大应力准则、最大应变准则与判断各向同性材料的破坏准则公式相同，只是当偏轴存在应力时，需要将偏轴应力转换为正应力.然而各向异性材料的形变应变能准则与各向同性材料的破坏准则公式不同.

Mises－Hill屈服准则是形变应变能准则建立的基础，这一理念是C.B.Norris在1950年首次提出的，针对二向平面的应力状态，其形变应变能方程为:

式中X为纵向强度，

Y为横向强度，

S为纵横剪切强度.

当公式(10)左端的各项之和大于或等于1时，其材料是失效的.

S.Tsai于20世纪60年代初提出了一个与公式(10)类似的强度准则，称之为Tsai－Hill准则，即:

只能在主方向材料的拉伸强度和压缩强度相同时才可以使用Tsai－Hill准则.考虑正交各向异性脆性材料存在拉压强度不相等的情况，因此Hoffman引入了应力分量奇此项，进而获得了形变应变能准则的另一种表达式:

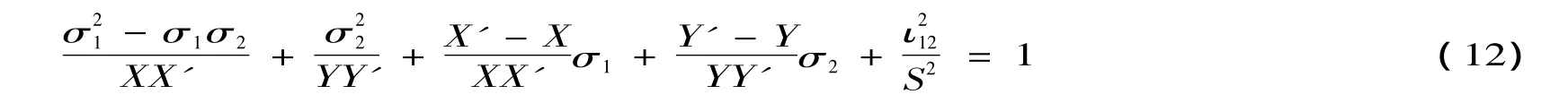
式中X为纵向拉伸强度，X'为纵向压缩强度，Y为横向拉伸强度，Y'为横向压缩强度，S——纵横剪切强度.当X=X'，Y=Y'时，式(12)就变为Tsai－Hill准则.

除以上所述的破坏准则外，Tsai－Wu准则同样得到了广泛使用，同公式(12)相比较，其不同在于 σ1σ2交叉项前面的系数，定在了 － 0.5到0之间［3］.

最大应力最大应变准则与以上四条形变应变能破坏准则的主要区别在于考虑了应力间的关联性.由于最大应力准则、最大应变准则使用非常简便，因此成为复合结构设计者使用最为广泛的破坏准则.有文献称，实验结果表明对低模量复合材料适合采用最大应力准则，而最大应变准则是剪切模量低的复合材料的代表.而针对无压应力的复合材料飞轮转子，则采用Tsai－Hill准则更加精确.正因为Tsai－Hill准则和实验所得的结果拥有合理的一致性，因此，它更适合用于复合材料飞轮转子的破坏分析，不过，Tsai－Hill准则存在不能给出构件失效形式的不足.

3 飞轮转子的静力分析

飞轮转子在高速旋转状态下会产生强大的离心惯性力，该离心力导致复合材料飞轮转子的内部出现应力，若该应力超过了复合材料的强度极限，则飞轮转子就会被破坏，因此，需要运用有限元软件ANSYS对高速旋转的复合材料飞轮转子进行应力分析.由于飞轮转子几何结构、约束情况均对称于转子的轴线，而且飞轮转子沿轴向z方向上不存在力的作用，故此方向上没有发生位移，而在飞轮转子的内侧，因为存在中轴惯性力的作用，会产生一个径向的分布力.因此，高速旋转飞轮转子的有限元分析可以作为平面问题来处理，故飞轮厚度值在有限元分析时可以忽略.

根据飞轮实际工作空间及上章所得飞轮转子结构尺寸，选取外径、内径分别为R=0.455m，r=0.373m，轴向高度h=1.16m的复合材料飞轮转子.

图1 单层复合材料储能飞轮模型Fig.1 Energy storage flywheel single－layer composite material model

本文讨论如图1所示的单层复合材料储能飞轮转子，选取碳纤维环氧树脂(T700/E－765Epoxy)复合材料.将单层的复合材料储能飞轮转子模型导入ANSYS并进行网格划分后，结果如图2所示:

图2 飞轮转子网格划分图Fig.2 The flywheel rotor meshing diagram

笔者采用扫掠网格划分法，共得到了18960个节点，3360个单元，网格是六面体单元，可使分析结果更加精确，并且网格成排分布，整体排列规则，这有利于载荷的施加和收敛的控制.

在通过ANSYS进行求解之前，需要将坐标系转化为圆柱坐标系，在正确设置约束及惯性载荷的作用下，得到飞轮转子转速为16000rpm时的应力分析结果，如图3和图4所示:

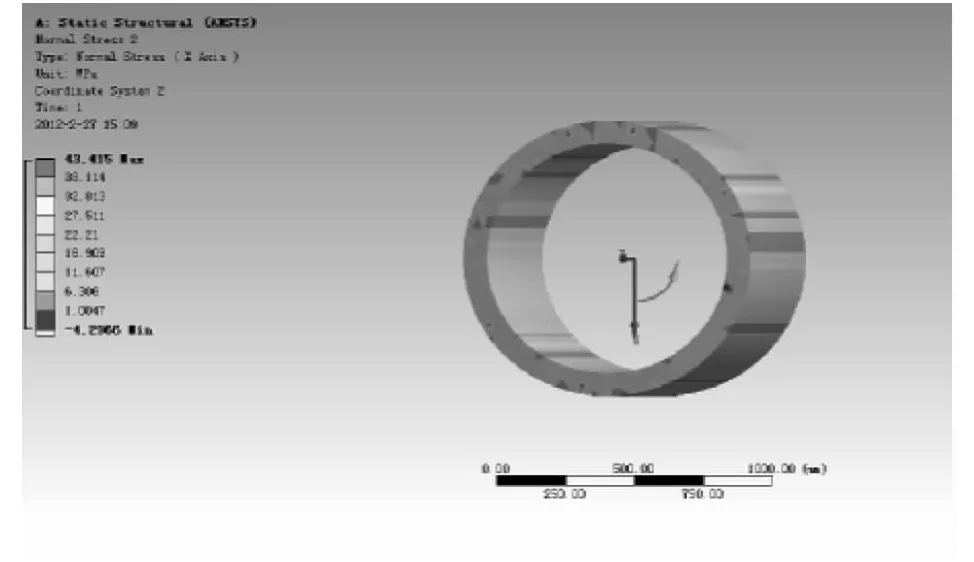
图3 飞轮转子径向应力图Fig.3 The flywheel rotor radial stress diagram

图4 飞轮转子环向应力图Fig.4 The flywheel rotor ring to the stress diagram

4 飞轮转子应力理论计算

空心圆盘的最大环向应力产生于内半径处，而径向最大应力发生在r =处，高速旋转的复合材料飞轮转子所受的最大径向应力和最大环向应力分别为［4］:

其中[ σθ]，[ σr]—— 飞轮材料的周向和径向强度极限.

高速旋转状态下飞轮转子所受的径向应力在数值上要比其所受的环向应力小的多，然而，对于高强度复合材料环向缠绕的圆环飞轮转子，其径向的许用应力 [ σh]远远小于其环向的许用应力 [ σθ]，因此当这种环向缠绕的圆环飞轮转子处于高速旋转的工作状态时，极有可能因为其径向强度的不足而导致飞轮转子的失效或破坏，因此，只需考虑径向应力是否满足材料强度要求，即需要理论计算验证飞轮转子所受径向应力是否超出复合材料径向强度极限.

将λ=0.8、a=0.455m、b=0.363m、v=1273m/s及所选材料性能参数代入上式得:

5 结论

复合材料飞轮处于高速旋转状态下，其离心应力不容忽视，本文通过ANSYS静力分析模块对高速旋转的复合材料飞轮转子进行应力分析，将分析结果与理论计算进行比较，最后得出运用ANSYS静力分析模块进行分析而获得的结果与理论计算结果非常接近，为以后复合材料飞轮转子的应力分析提供一定的参考依据.

［1］王震鸣.复合材料力学和复合材料结构力学［M］.北京:机械工业出版社，1991.

［2］姜晋庆，张择.结构弹塑性有限元分析法［M］.北京:中国宇航出版社，1990.

［3］杨庆生.复合材料细观结构力学与设计［M］.北京:中国铁道出版社，2000.

［4］张兴蕾.复合材料储能飞轮转子的设计［J］.机械，2012.39(5):33－35.

［责任编辑:闫 昕］