基于多通道图卷积自编码器的图表示学习

袁立宁，胡皓，刘钊

（1.中国人民公安大学 信息网络安全学院，北京 100038；2.中国人民公安大学 研究生院，北京 100038）

0 概述

在现实世界中，图被广泛用于表示实体和实体间的关系，例如分子结构、通信网络、社交网络和犯罪网络等。从图数据中提取信息，用于节点分类［1］、节点聚类［2］、可视化［3］等下游任务具有重要的研究意义。但是，图作为非欧氏数据，蕴含的信息往往具有高维隐式特性，这导致卷积神经网络和循环神经网络等针对欧氏数据设计的深度学习模型很难直接应用。因此，将图数据从非欧氏空间转换到欧氏空间是处理和分析图数据的基础和关键。图表示学习，也称图嵌入，是将图中节点转换为保留原始图关键信息的低维节点向量，从而实现非欧氏数据到欧氏数据的转换。按照提取图信息的不同，图表示学习模型可分为基于图结构的方法和基于图特征的方法。

基于图结构的方法仅使用拓扑结构生成节点表示。例如，Deepwalk［4］使用随机游走采样图的拓扑结构生成节点序列，通过Skip-Gram［5］最大化序列中窗口范围内节点之间的共现概率，生成低维嵌入。Node2Vec［6］在Deepwalk 的基础上，引入有偏的随机游走，增加邻域搜索的灵活性，生成质量更高、信息更丰富的嵌入表示。结构深度网络嵌入（Structural Deep Network Embedding，SDNE）［7］使用最简单的线性全连接层构建多层欠完备自编码器对图数据进行降维，同时引入拉普拉斯特征映射（Laplacian Eigenmaps，LE）［8］保留一阶相似度信息，增大非零项重构损失保留二阶相似度信息，使生成嵌入同时保留局部结构信息和全局结构信息。由于上述方法只是针对图拓扑结构的单一表示学习，缺乏对节点属性信息的提取，因此限制了模型在属性图上的表示能力。

基于图特征的方法同时使用图的拓扑结构和节点属性生成节点表示。深度属性网络嵌入（Deep Attributed Network Embedding，DANE）［9］在SDNE 的基础上，增加了属性信息自编码器，生成节点属性向量。为了在低维嵌入中保留拓扑结构和属性信息，DANE 将属性向量和拓扑向量进行拼接。由于SDNE 和DANE 使用最简单的线性编码器，难以有效捕获图的高阶非线性信息，限制了模型的表示能力。图神经网络（Graph Neural Network，GNN）［10］通过特征传播聚合邻域信息，解决了属性和拓扑融合问题。例如，图卷积网络（Graph Convolutional Network，GCN）［11］使用卷积运算迭代地聚合节点邻域向量，同时使用当前和先前迭代中的表示生成下一时刻的表示。在多次迭代后，GCN 学习到的节点表示能够同时表征属性和拓扑信息。图注意力网络（Graph Attention Network，GAT）［12］在原始GCN 上使用注意力机制，对邻近节点特征向量加权求和，分配不同的权值，构建图注意力卷积核。变分图自编码器（Variational Graph Autoencoder，VGAE）［13］以变分自编码器（Variational Autoencoder，VAE）［14］为基础架构，使用GCN 编码器和内积解码器生成低维表示。GALA［15］采用完全对称的图卷积编码器和解码器生成低维表示。相较于仅使用GCN 编码器的VGAE，GALA 的对称结构能够同时在编码和解码过程中使用结构信息。基于GCN 强大的表示能力，众多图分析任务性能显著提升。但近期研究表明，GCN 融合节点属性和拓扑结构的能力是有限的。LI等［16］证明了GCN 仅是对节点属性执行拉普拉斯平滑使节点逐渐收敛，使得GCN 无法学习结构和属性之间的深度关联信息。WANG等［17］分别在拓扑图和属性图上传播节点特征，同时采用半监督的方式进行训练，改善了节点属性和拓扑结构信息的融合。

本文在上述工作的基础上，提出基于多通道图卷积自编码器的无监督图嵌入模型MC-GCAE。通过构建特定信息卷积编码器和一致信息卷积编码器，在属性空间和拓扑空间传播节点特征的同时，保留属性和拓扑之间的关联信息，生成属性嵌入、拓扑嵌入和一致性嵌入，并采用与编码器对称的解码器还原编码过程，实现无监督学习。在嵌入生成过程中，使用重构损失、局部约束和一致性约束进行优化，其中，局部损失用于保留局部拓扑结构信息，一致性约束用于增强属性和拓扑之间的关联信息。另外，MC-GCAE 分别采用平均和拼接的方式融合不同编码器生成的嵌入，充分保留原始图信息。

1 拓扑和属性信息保留能力实验

本节通过3 个直观的实验以验证基于GCN 的自编码器模型保留节点属性和拓扑结构信息的能力。首先，分别建立节点标签与节点属性和拓扑结构的依赖关系，并构建随机拓扑相关属性图、相关拓扑随机属性图和相关拓扑相关属性图。然后，使用相同参数及重构损失训练GCN 编码器和线性编码器，生成低维嵌入表示。最后，通过比较生成嵌入在节点分类任务中的实验表现，以验证模型保留节点属性和拓扑结构信息的能力。

1.1 实验1：随机拓扑结构与相关节点属性

随机拓扑相关属性图由900 个节点构成，节点之间边生成的概率为0.03，每个节点有50 维的节点属性。其中，节点属性通过3 个高斯分布生成（协方差相同但中心距离很远），并依据所在中心将其分为3类。对于随机拓扑相关属性图，每个节点的标签与节点属性高度相关且与拓扑结构无关。在节点分类实验中，使用30%的节点标签和随机拓扑相关属性图的嵌入表示训练分类器，使用50%的节点标签进行测试，最终GCN 编码器的预测准确率为35.1%，线性编码器的预测准确率为41.1%。

1.2 实验2：相关拓扑结构与随机节点属性

相关拓扑随机属性图由900 个节点构成，使用随机区块模型（Stochastic Block Model，SBM）［18］将节点分为3 个不同社区（节点数分别为0～299、300～599、600～899），社区内部节点成边概率为0.03，社区外部节点成边概率为0.001 5，根据所在社区不同将节点分为3类，每个节点随机生成50 维的节点属性。对于相关拓扑随机属性图，每个节点的标签与拓扑结构高度相关且与节点属性无关。在节点分类实验中，使用30%的节点标签和相关拓扑随机属性图的嵌入表示训练分类器，使用50%的节点标签进行测试，最终GCN 编码器的预测准确率为74.9%，线性编码器的预测准确率为85.6%。

1.3 实验3：相关拓扑结构与相关节点属性

相关拓扑相关属性图由900个节点构成，使用SBM将节点分为3 个不同社区（节点数分别为0～299、300～599、600～899），社区内部节点成边概率为0.03，社区外部节点成边概率为0.001 5，每个社区内的节点由高斯分布生成50 维节点属性，不同社区使用的高斯分布协方差相同但中心距离很远，根据社区和属性信息将节点分为3类。对于相关拓扑相关属性图，每个节点的标签与拓扑结构和节点属性高度相关。在节点分类实验中，使用30%的节点标签和相关拓扑相关属性图的嵌入表示训练分类器，使用50%的节点标签进行测试，最终GCN 编码器的预测准确率为78.9%，线性编码器的预测准确率为97.3%。

上述实验结果表明，基于GCN 的自编码器模型保留节点属性和拓扑结构信息的能力有限，甚至无法匹配简单的线性模型。在节点标签与原始图信息关联非常紧密的情况下，GCN 编码器未能充分提取相关信息改善下游任务实验表现。在现实世界中，图数据的属性和拓扑信息通常更为复杂，因此需要对现有GCN 编码器模型进行改进，使生成的嵌入能够保留更丰富的原始图信息，增强模型的表征能力。

2 MC-GCAE 模型

本节首先给出MC-GCAE 模型的整体结构，然后介绍模型的编码器和解码器结构以及融合机制，最后分析模型的损失函数。

2.1 模型结构

MC-GCAE 是用于属性图G=（A，X）表示学习的无监督模型，其中：A∈Rn×n为图的邻接矩阵，n为节点个数；X∈Rn×d为节点属性矩阵，由节点属性向量xi∈R1×d堆叠构成，d为每个节点特征的维数。

MC-GCAE 由基于GCN 的编码器和解码器组成，模型整体结构如图1 所示（彩色效果见《计算机工程》官网HTML 版）。为了有效捕获节点属性、拓扑信息以及拓扑与属性之间的关联信息，MC-GCAE 分别从属性空间和拓扑空间对节点邻域的特征信息进行聚合。首先，使用GCN 构建两个特定信息卷积编码器，利用属性邻接矩阵AF、拓扑邻接矩阵AT和属性矩阵X生成属性嵌入YF和拓扑嵌入YT。然后，使用GCN 构建一致信息编码器，采用参数共享的方式生成YCF和YCT，进而生成保留属性和拓扑之间的关联信息的一致性嵌入YC。通过对称解码器，将上述编码器生成的嵌入矩阵还原为属性矩阵X，实现无监督学习。在生成嵌入矩阵时，使用重构损失Lrecovery、局部约束Llocal和一致性约束LC进行优化，其中，Llocal用于保留AF和AT局部结构信息，LC用于增强YCF和YCT的关联信息。为使最终嵌入Y能够保留原始图的关键信息，分别使用平均和拼接的方式对YF、YC和YT进行融合。

图1 MC-GCAE 模型结构Fig.1 Structure of the MC-GCAE model

2.2 多通道编码器

2.2.1 属性相似度邻接图

为了捕获属性空间中节点的结构关系，需要计算任意两个节点属性向量xi和xj的相似度，构建相似度矩阵。使用余弦相似度构建相似度矩阵S：

然后，从S中选择k对最相似的节点对构建图的边集，生成基于属性相似度的k 近邻图GF=(AF，X)，其中AF为k 近邻相似度图的邻接矩阵。

2.2.2 特定信息卷积编码器

GCN 能够利用卷积运算从图G中提取特征，生成包含拓扑结构和节点属性信息的低维嵌入。在通常情况下，GCN 使用节点属性矩阵X与邻接矩阵A作为原始输入，各层之间的传播公式表示如下：

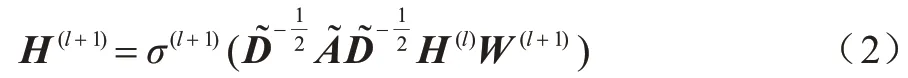
其中：W(l+1)为第l+1 层图卷积的参数矩阵；σ为激活函数；H（l）为激活矩阵，且H（0）=X。

使用双层GCN 以及LeakyReLU 激活函数构建特定信息卷积编码器，对于属性相似度图使用节点属性矩阵X与邻接矩阵AF作为原始输入，生成如下嵌入表示：

对于拓扑图GT=(AT，X)，特定信息卷积编码器使用节点属性矩阵X与邻接矩阵AT作为原始输入，采用与属性图相同的计算方式，生成如下嵌入表示：

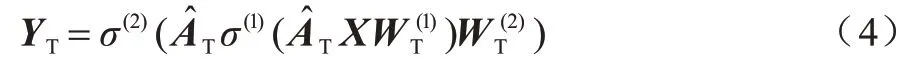
其中：YT为捕获拓扑空间特定信息的拓扑嵌入。

2.2.3 一致信息卷积编码器

节点属性和拓扑结构通常不是完全无关的，但是两者之间的重要性、关联性通常难以确定。因此，在生成的嵌入表示中，不仅要分别提取属性空间和拓扑空间的特定信息，还需要提取这两个空间共享的一致信息。受WANG等［17］工作的启发，设计一个具有参数共享策略的Consensus-GCN 编码器，捕获两个空间的关联信息。首先，利用Consensus-GCN从属性近邻图中提取节点嵌入YCF：

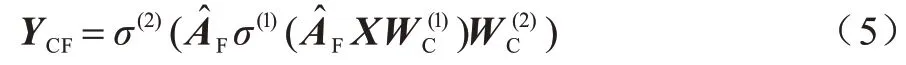
然后，在使用Consensus-GCN 编码器从属性图中学习节点嵌入的同时，为了提取属性图和拓扑图的一致信息，对每一层Consensus-GCN 共享相同的权重矩阵：

最后，使用共享参数矩阵可以从两个空间获取属性和拓扑的一致信息。将编码器部分生成的YCT和YCF进行融合，生成属性和拓扑空间的一致性嵌入YC：

2.3 对称解码器

MC-GCAE 的编码器部分为多通道GCN。解码器部分采用与编码器具有相同层数的对称解码器，每个解码器层都反转对应卷积编码器层的编码过程，使模型能够在没有任何监督信息的情况下学习节点表示。解码器部分的层间传播公式表示如下：

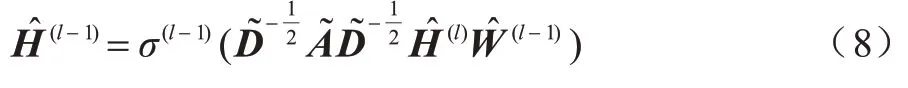
对于特定信息卷积编码器生成的YF和YT，双层对称解码器的恢复过程表示如下：

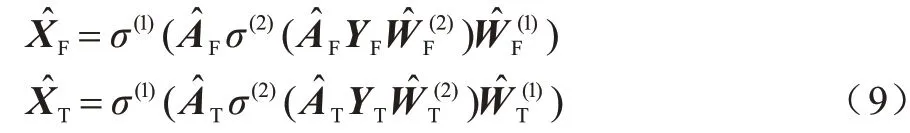
其中：和分别表示特定信息解码器利用拓扑图和属性图重构的属性矩阵。

对于一致信息卷积编码器生成的YCF和YCT，在解码器部分同样使用参数共享策略，恢复过程表示如下：

其中：和分别表示一致信息解码器利用拓扑图和属性图重构的属性矩阵。

2.4 嵌入融合机制

MC-GCAE 利用编码器生成了两个包含特定信息的嵌入YF和YT，以及一个包含一致信息的嵌入YC。为使生成的最终嵌入Y能够保留更多原始图信息，分别采用平均和拼接两种方式融合嵌入矩阵YF、YC和YT。

MC-GCAE-avg 采用平均的方式生成最终嵌入Yavg，其表达式如下：

MC-GCAE-concat 采用拼接的方式生成最终嵌入Yconcat，其表达式如下：

其中：||表示拼接操作。

2.5 损失函数

2.5.1 重构损失

在一般情况下，AE 的优化目标是最小化输入和输出的重构误差，其损失函数表示如下：

最小化重构误差不能显式地保持样本之间的相似性，但能够平滑地捕获数据流形，进而隐式地保持相似性。由于图的属性信息使用0-1 矩阵表示，使得X中非零元素个数远小于零元素个数，如果直接使用X和，则会导致解码器更倾向于重构零元素。为解决上述问题，修改原有LAE函数，对非零元素的重构误差施加比零元素更大的惩罚：

MC-GCAE 使用四组编码器-解码器结构，每组重构损失均使用式（14）进行优化，完整的重构损失Lrecovery表示如下：

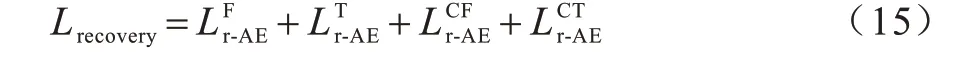
2.5.2 局部约束

除了利用重构损失作为全局约束以外，捕获图的局部结构信息也十分重要。LE 能够从局部近似的角度构建节点之间的关系，使相连节点在嵌入空间中尽可能靠近，进而使生成嵌入中保留局部结构信息。LE 的损失函数表示如下：

其中：Aij表示邻接矩阵的元素。

对于YF、YT、YCF和YCT，在生成过程中均使用LE损失进行约束，因此局部约束Llocal表示如下：

2.5.3 一致性约束

Consensus-GCN 使用共享权值矩阵的方式保持YCT和YCF中的一致信息。为了进一步增强这种一致性，在MC-GCAE 中引入一致性约束函数。首先，使用L2 范数将嵌入矩阵归一化为YCTnorm和YCFnorm。然后，利用上述归一化矩阵捕获图中节点间的相似性信息，生成相似性矩阵SCT和SCF：

由于一致性表示矩阵SCT和SCF是相似的，因此一致性约束函数表示如下：

结合重构损失、局部约束和一致性约束，MCGCAE 完整的损失函数表示如下：

其中：ε为控制Llocal的超参数；Lreg为防止参数过拟合的正则化项。Lreg计算如下：

3 实验与结果分析

3.1 实验设置

3.1.1 数据集

为了验证低维节点嵌入的表示能力，在6 个真实世界的数据集上对MC-GCAE 和基线模型进行评估。表1 为数据集的统计信息，具体说明如下：

表1 数据集统计信息 Table 1 Statistics of the datasets

1）网页网络：Cornell［19］和Texas［19］是卡耐基梅隆大学采集的网页数据集的两个子集，其中，节点表示网页，边表示网页之间的超链接，节点属性是网页的词袋表示。这些网页被人工分为学生、项目、课程、工作人员和教师5类。Cornell 用于节点分类和节点聚类任务，Texas 用于节点分类任务。

2）引文网络：Cora［20］和Citeseer［20］是标准的引文网络数据集，其中，节点表示论文，边表示一篇论文对另一篇论文的引用，节点属性是论文词袋表示，节点标签是论文学术主题。Cora 用于节点分类任务，Citeseer 用于节点分类和节点聚类任务。

3）社交网络：BlogCatalog［21］是博客网站的数据集，其中，节点表示博主，边表示博主间的社交关系，节点属性由博主信息的关键字构造，标签代表作者提供的主题类别。Flickr［22］是图片分享网站数据集，用户通过图片分享进行互动，其中，节点表示用户，边表示用户间的友谊关系，节点标签根据用户兴趣组划分。BlogCatalog 和Flickr 均用于节点分类任务。

3.1.2 基线模型

将以下模型作为基线模型：

1）Deepwalk：以邻接矩阵作为输入，首先利用随机游走获取节点序列，然后使用Skip-Gram 算法最大化节点共现概率，生成节点表示。

2）SDNE：以邻接矩阵作为输入，利用深度线性自编码器以及图的一阶、二阶相似度，生成并捕获高度非线性的节点表示。

3）SSDNE［23］：以邻接矩阵作为输入，在SDNE 的基础上增加传统链路预测相似度矩阵（Katz 矩阵）作为约束条件，生成节点表示。

4）DANE：以属性矩阵和邻接矩阵作为输入，在SDNE 的基础上增加独立的属性编码器，将深度线性自编码器生成的属性嵌入和拓扑嵌入进行拼接，生成节点表示。

5）AENEA［24］：以邻接矩阵作为输入，通过随机冲浪生成共现概率矩阵后，计算PPMI 矩阵作为深度线性自编码器输入，使用图的一阶、二阶相似度作为约束，生成节点表示。

6）GALA：以属性矩阵和邻接矩阵作为输入，采用完全对称的GCN 自编码器生成节点表示，在编码和解码过程中同时使用结构和属性信息。

7）GATE［25］：以属性矩阵和邻接矩阵作为输入，编码器各层首先通过self-attention 为邻居节点分配不同权重，然后聚合邻域信息生成节点表示，解码器对编码过程进行反转。

8）GASN［26］：以属性矩阵和邻接矩阵作为输入，使用改进GCN［26］编码生成节点表示，在解码器部分利用内积解码器重构邻接矩阵，采用对称GCN 解码器重构属性矩阵。

9）VGAE：以属性矩阵和邻接矩阵作为输入，编码器首先利用GCN 获得节点表示的概率分布，然后在分布中采样生成节点表示，最后使用内积解码器重构图的邻接矩阵。

10）OSA-VGAE［27］：以属性矩阵和邻接矩阵作为输入，在VGAE 的基础上引入One-Shot 聚合［28］增强深层模型性能，生成节点表示。

3.1.3 参数设置

所有基线模型按照原始论文中建议的参数进行初始化，并对部分模型进一步调整，以获取基线的最佳性能。对于MC-GCAE，隐藏层的维度hhidden∈｛512，768｝，生成嵌入的维度d∈｛25，26，27｝；属性邻接图近邻数k∈｛2，3，…，20｝；损失函数中惩罚系数b∈｛1，3，5，7，10｝，超参数ε∈｛10-3，10-2，10-1｝。表2 为MC-GCAE 的参数设置。

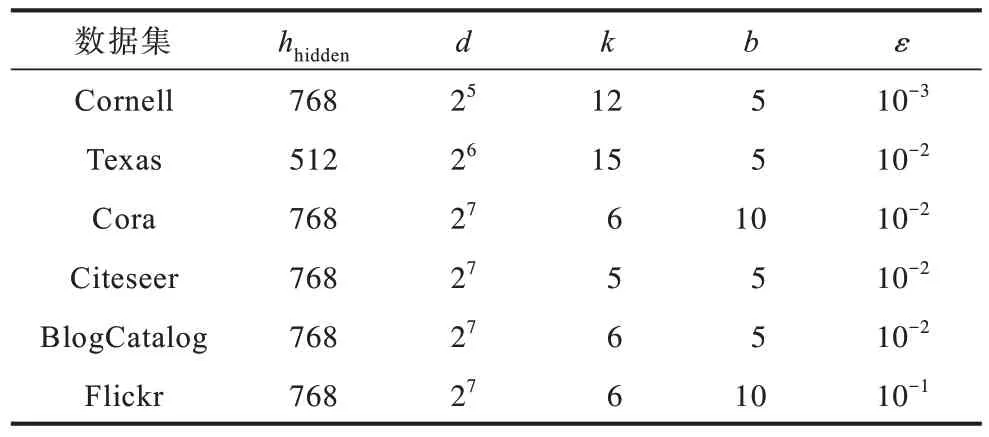
表2 MC-GCAE 参数设置 Table 2 Parameter setting of MC-GCAE

3.1.4 评价指标

为了评估模型在节点分类、节点聚类上的性能，使用Macro-F1、Micro-F1、聚类精度（Clustering Accuracy，Cluster-Acc）和归一化互信息（Normalized Mutual Information，NMI）作为评价指标。

在多标签节点分类任务中，Micro-F1 计算公式如下：

其中：P表示精确率；R表示召回率。

Macro-F1 计算公式如下：

其中：L表示标签集；F（l）是标签l的F1值。

在节点聚类任务中，给定真实标签li和聚类标签zi，Cluster-Acc 计算公式如下：

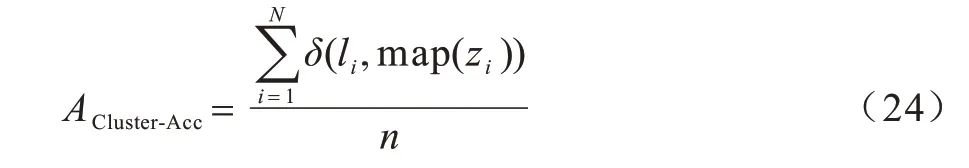
其中：n为节点数；map（·）为映射函数，使用Hungarian 算法［29］映射聚类标签和真实标签；δ（·）函数用于判别映射标签和真实标签是否一致，相同结果为1，不同结果为0。

节点聚类任务还采用NMI 评估模型性能，计算公式如下：

其中：NMI 用于度量M1和M2聚类结果之间的相似性；H（·）表示信息熵。

3.2 节点分类对比

本节通过多标签分类任务评估不同模型性能。生成的低维嵌入作为逻辑回归分类器的输入，对于每个数据集，以10%为间隔，随机抽取10%～50%的节点表示作为训练数据，剩余节点中抽取50%作为测试集，各模型采用相同的数据集划分，记录Micro-F1和Macro-F1。节点分类实验结果如图2～图4 所示（彩色效果见《计算机工程》官网HTML 版），由图2～图4 可以得出：

图2 网页网络的Micro-F1 和Macro-F1Fig.2 Micro-F1 and Macro-F1 on the Web networks

1）在大多数情况下，MC-GCAE 能够超过基线模型的分类性能，特别是在Cornell、BlogCatalog 和Flickr数据集上，MC-GCAE 的Micro-F1 和Macro-F1 值始终高于基线模型。上述结果表明，MC-GCAE 能够从不同特征空间中捕获原始图信息，并将其保留在生成的低维嵌入中，提升节点分类任务的实验表现。

2）在大部分数据集上，仅使用GCN 编码解码的GALA 的实验表现不佳，特别是在Cora、Citeseer 和BlogCatalog 数据集上，GALA 的Micro-F1 和Macro-F1 值显著低于其他模型。上述结果表明，仅使用重构损失的GCN 编码器提取节点属性和拓扑结构信息的能力有限，在生成嵌入中未能充分保留原始图相关信息。

3）在BlogCatalog 和Flickr 数据集上，基于线性编码器的基线模型的实验表现显著优于基于GNN编码器的基线模型。上述结果进一步表明，基于GCN 及其变体的编码器模型在无监督条件下不能有效提取结构、属性及其关联信息，导致模型分类性能低于使用随机游走的Deepwalk 以及采用简单线性编码器的SDNE、SSDNE、DANE 和AENEA。

4）在不同数据集上，同一基线模型的分类表现差异明显。例如：DANE 在网页网络Texas 数据集上表现出色，但在同类型且统计信息相似的Cornell 数据集上表现不佳；GATE 在引文网络Citeseer 数据集上表现出色，但在社交网络BlogCatalog 和Flickr 数据集上表现不佳。上述结果表明，基线模型在处理不同数据集时，泛化能力有限。与基线模型相反，MC-GCAE 在所有数据集上均取得了良好的实验性能，证明了MC-GCAE强大的泛化能力。此外，与基线模型相比，MC-GCAE使用10%～30%的训练数据即可显著提升分类任务的性能表现。

图3 引文网络的Micro-F1 和Macro-F1Fig.3 Micro-F1 and Macro-F1 on the citation networks

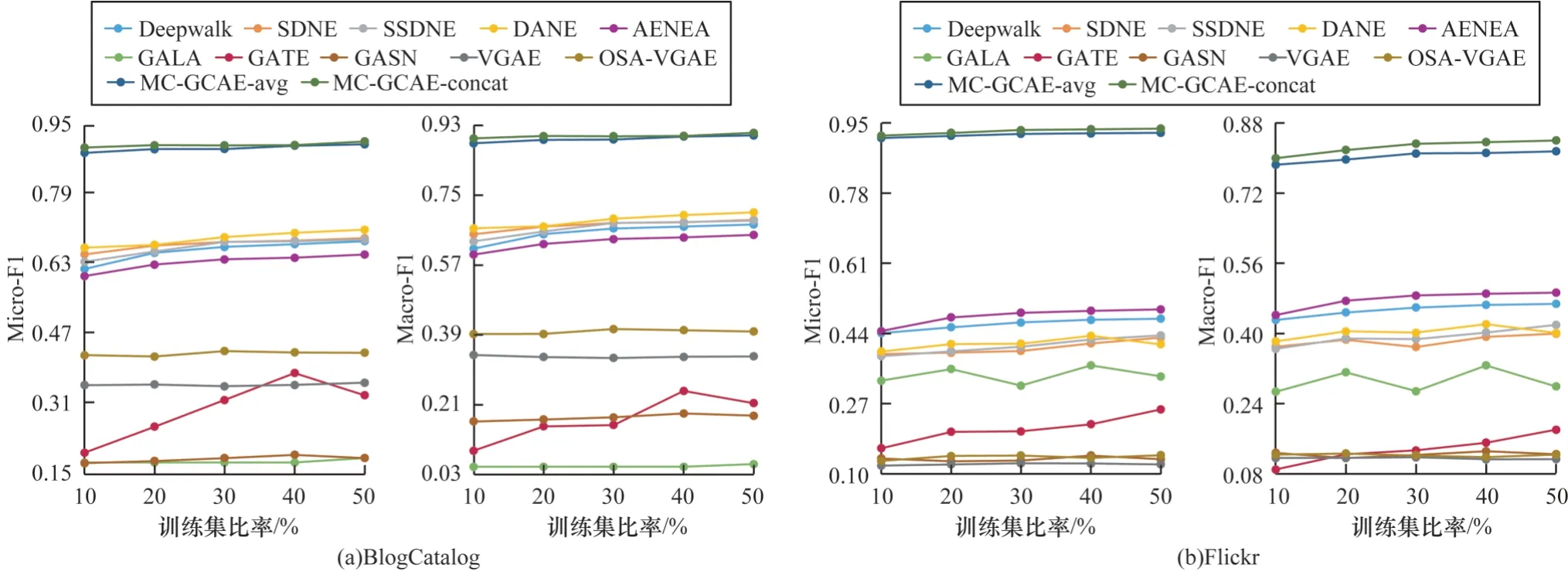
图4 社交网络的Micro-F1 和Macro-F1Fig.4 Micro-F1 and Macro-F1 on the social networks

5）对比基于图结构和基于图特征基线的实验结果，虽然基于图特征的方法输入的原始图信息更丰富，但模型融合和保留图特征的能力有限，属性空间和拓扑空间的关键信息相互抵消，导致性能差于基于图结构的方法。为改善上述问题，MC-GCAE 通过增加一致性空间特征提取，平衡生成嵌入中的属性和拓扑信息，提升模型的表示能力。

6）对 比MC-GCAE-avg 和MC-GCAE-concat 的实验结果，在大部分情况下，拼接方式优于平均方式。特别是在Texas 数据集上，由于属性信息明显多于节点数和边数，采用平均方式的MC-GCAE-avg 弱化了属性信息的比重，使其性能差于采用拼接方式的MC-GCAE-concat。在同样属性信息较多的Cornell 数据集上，虽然MC-GCAE-avg 的Micro-F1值在部分训练集比率下高于MC-GCAE-concat，但是随着训练集比率提高，MC-GCAE-concat 的Macro-F1 值逐渐优于MC-GCAE-avg，同样证明了拼接方式能够保留更多的图信息，提升分类性能。

3.3 节点聚类对比

由于各模型生成的嵌入维度不同，为了保证公平性，首先使用降维算法［3，30］将所有模型生成的嵌入降至2维，然后执行K-means++［31］实现无监督节点聚类。在K-means++算法中，K值设置为Cornell 和Citeseer 数据集的类别数，运行算法10次，记录Cluster-Acc 和NMI的平均值。节点聚类的实验结果如表3 所示，其中，排名第一的实验结果用加粗表示，排名第二的实验结果用下划线表示。

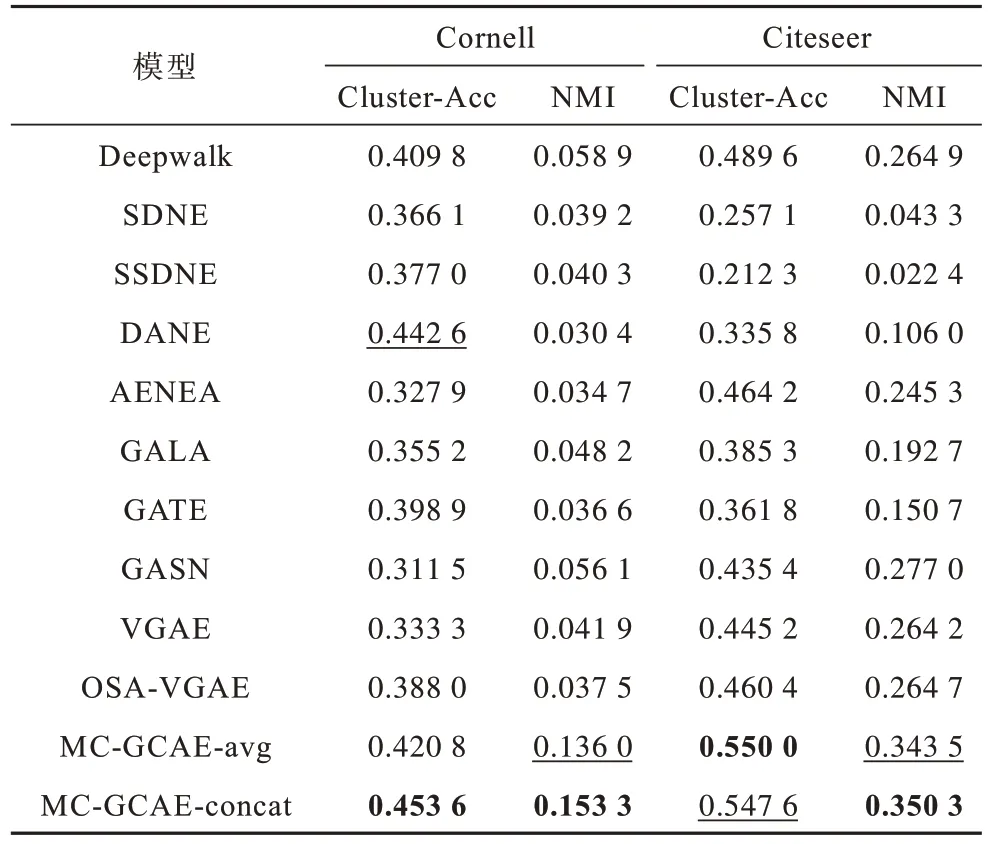
表3 节点聚类实验结果 Table 3 Experiment results of the node clustering

由表3 可以得出：

1）相较基线模型，MC-GCAE 取得了最佳聚类性能，在Cornell数据集上Cluster-Acc 和NMI 相比于表现最优的基线模型提升了2.49%和160.27%，在Citeseer数据集上Cluster-Acc 和NMI 相比于表现最优的基线模型提升了11.84%和34.03%。上述实验结果进一步表明，同时使用属性、拓扑和一致信息的MC-GCAE 在生成的低维嵌入中充分保留了原始图信息，显著提升了模型在无监督聚类任务中的实验表现。

2）在两个数据集上，同一基线模型的聚类表现差异明显。例如：DANE 在Cornell 上的Cluster-Acc 显著优于其他基线模型，但在Citeseer 上表现不佳；基于变分自编码器架构的GASN 和VGAE 在Citeseer 上的实验表现优于Cornell。上述结果进一步表明，基线模型处理不同数据集的泛化能力有限。MC-GCAE 在两个数据集上均取得了良好的实验性能，再次证明了其具有较强的泛化能力。

3）基于GCN 及其变体的自编码器模型GALA、GATE、GASN、VGAE 和OSA-VGAE 保留节点属性和拓扑结构信息的能力有限，在两个数据集上实验表现均差于基于图结构的Deepwalk。此外，在训练过程中仅使用最大化共现概率和负采样进行优化的Deepwalk 缺乏明确优化函数，并且仅使用邻接矩阵作为输入，上述特性使得Deepwalk 的实验性能远低于保留属性、拓扑和一致信息的MC-GCAE。

3.4 可视化和变体分析

在节点表示中蕴含了图的属性和拓扑信息，对其进行可视化后，能够直观地反映原始图的某些特征。对于可视化任务，首先使用t-分布随机邻域嵌入（t-distributed Stochastic Neighbor Embedding，t-SNE）［3］将节点表示的维度降低到2，然后将其在2 维平面上进行可视化，最后根据Citeseer 数据集的类别标签，将节点标记为6 种不同的颜色。各模型生成嵌入的可视化结果如图5 所示（彩色效果见《计算机工程》官网HTML 版）。

从图5 可以看出：多数基线模型生成嵌入的可视化效果很差，不同类型的节点大多混合在一起，基本是无序的；MC-GCAE 的可视化效果明显好于上述模型，学习到的节点表示有较高的类内相似性和类间界限。可视化结果直观反映了模型保留同一社群节点相似特征的能力，证明了MC-GCAE 分别从属性空间、拓扑空间和一致性空间提取图信息的方式能够充分保留原始图信息，使同类节点在低维嵌入空间彼此接近。

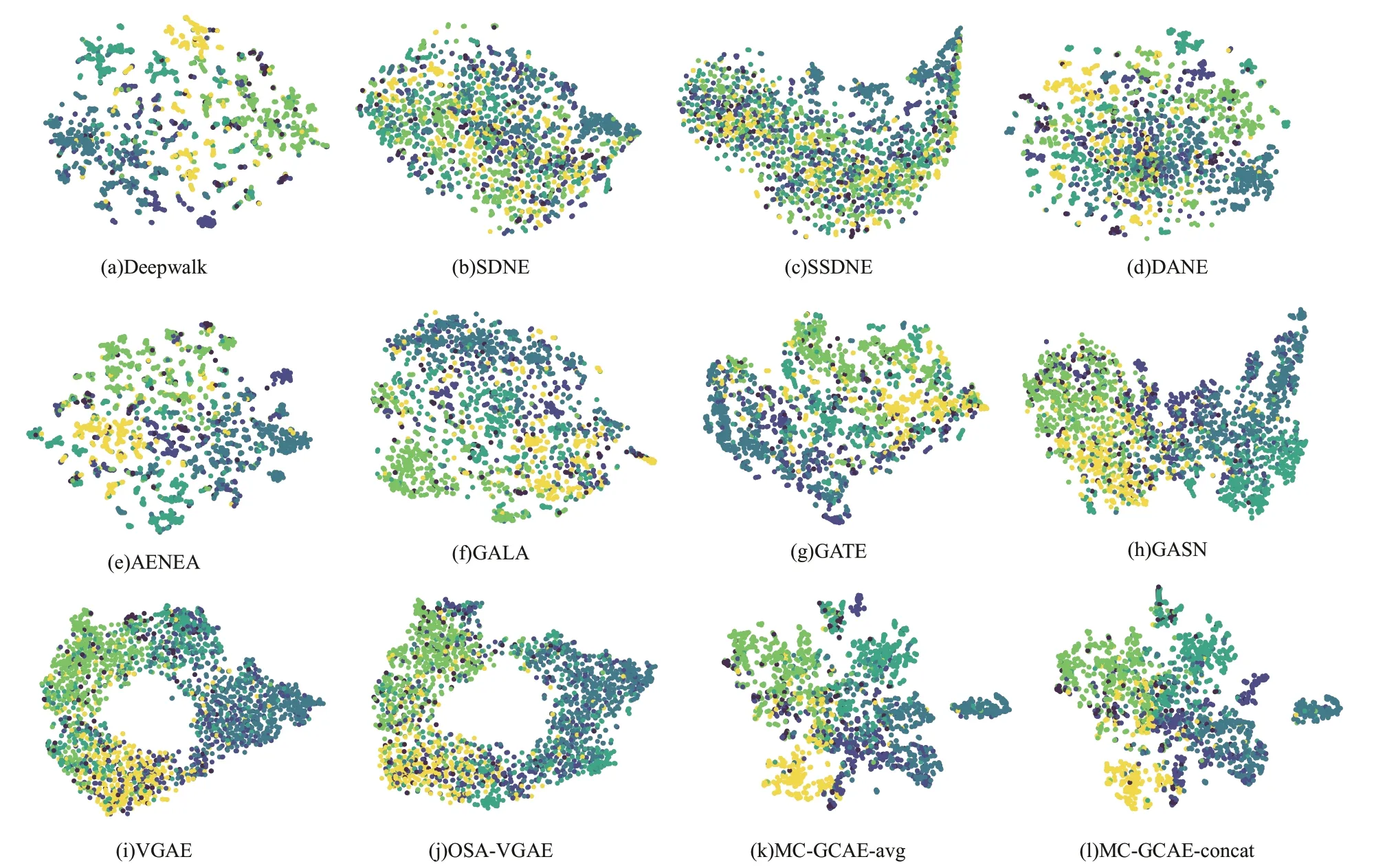
图5 Citeseer 数据集上节点表示可视化Fig.5 Visualization of node representations on the Citeseer dataset

为了进一步验证MC-GCAE的有效性，在Cornell、Citeseer 和BlogCatalog 数据集上进行节点分类实验（40%数据作为训练集，50%数据作为测试集），对比MC-GCAE（拼接融合）及其变体的实验性能。各变体相关信息如下：

1）GCAE-T：MC-GCAE 的拓扑信息编码组件，用于生成拓扑嵌入YT。

2）GCAE-A：MC-GCAE 的属性信息编码组件，用于生成属性嵌入YF。

3）GCAE-C：MC-GCAE 的属性和拓扑一致信息编码组件，用于生成一致性嵌入YC。

4）GCAE-A&T：MC-GCAE 的特定信息编码部分，拼接拓扑嵌入YT和属性嵌入YF。

从图6 的实验结果可以得出：

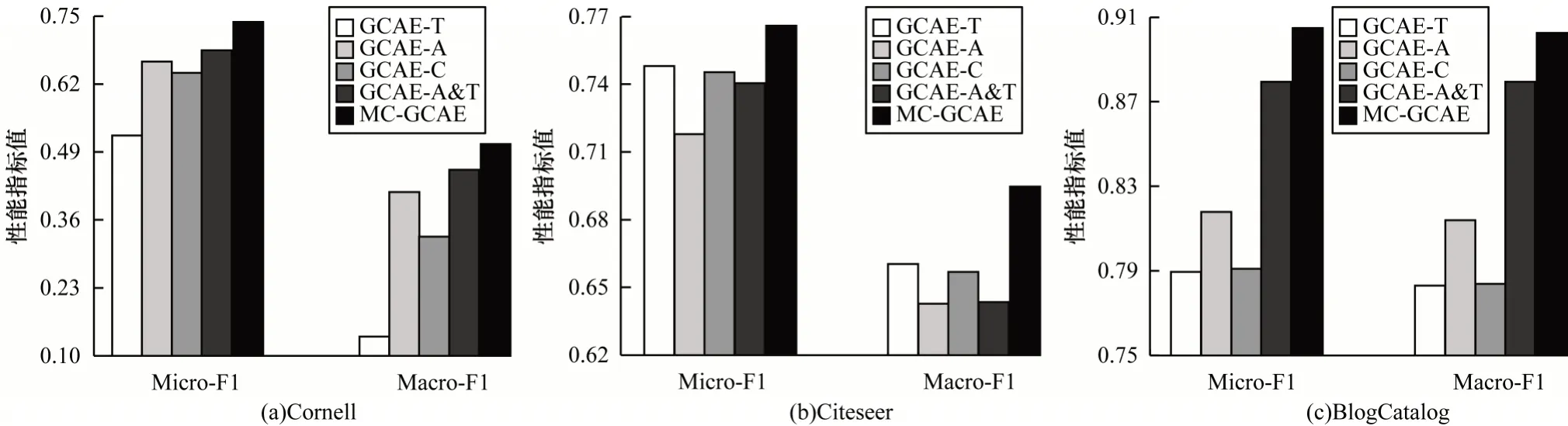
图6 MC-GCAE 及其变体的实验结果 Fig.6 Experimental results of MC-GCAE and its variants

1）在3 个数据集上，MC-GCAE 的实验结果始终优于4 个变体，证明了采用多通道方式学习属性信息、拓扑信息和一致信息的方式能够提升基于GCN自编码器模型保留原始图信息的能力。

2）在Cornell 数据集上，原始图的属性信息远超节点和边的数量，因此仅使用属性空间信息的GCAE-A 性能更为突出，优于仅使用拓扑信息的GCAE-T 和一致信息的GCAE-C，并且与同时使用拓扑信息和属性信息的GCAE-A&T 性能接近。

3）GCAE-T 和GCAE-A 的性能受实验数据影响明显，即属性信息丰富的图上GCAE-A 性能更好，拓扑信息丰富的图上GCAE-T 性能更好，而保留属性和拓扑一致信息的GCAE-C 性能始终在两者之间。

4）在3 个数据集上，GCAE-A&T 的实验性能始终差于MC-GCAE，这是因为同时使用拓扑嵌入、属性嵌入和一致性嵌入能够在最终嵌入中保留更丰富的原始图信息，增强模型的表示能力。此外，综合对比3 个数据集上的实验表现，MC-GCAE 比仅使用拓扑嵌入和属性嵌入的GCAE-A&T 更稳定。

3.5 参数分析

为了分析MC-GCAE 性能与参数的关联性，使用Texas 和Citeseer 数据集上的节点分类任务（10%数据作为训练集，50%数据作为测试集）进行参数实验。

为了验证k 近邻节点中不同k值对属性相似度图的影响，记录不同k值在Texas 和Citeseer 数据集上的分类性能，实验结果如图7 所示。由图7 可以看出，在Texas 和Citeseer 数据集上，Micro-F1 和Macro-F1 都呈现先上升后下降的趋势，过高和过低的k值表现均较为一般，这是因为k值过低属性图无法保留充足的属性空间信息，而k值过高属性图会生成大量噪声边降低模型性能。

图7 参数k 分析 Fig.7 Analysis of the parameter k

为了验证b值对模型性能的影响，记录不同b值在Texas 和Citeseer 数据集上的分类性能，实验结果如图8 所示。b值越大，模型越容易重构非零元素。当b=1时，模型将平等地重建非零元素和零元素，这使得其在属性信息稀疏的Citeseer 数据集上分类性能较差。当b值过大时，分类性能也会下降，原因在于模型执行重构更倾向保持非零项，忽略了零元素包含的属性之间的差异性信息。实验结果表明，在模型训练过程中既要关注非零元素包含的属性信息，又要关注零元素包含的属性差异信息。

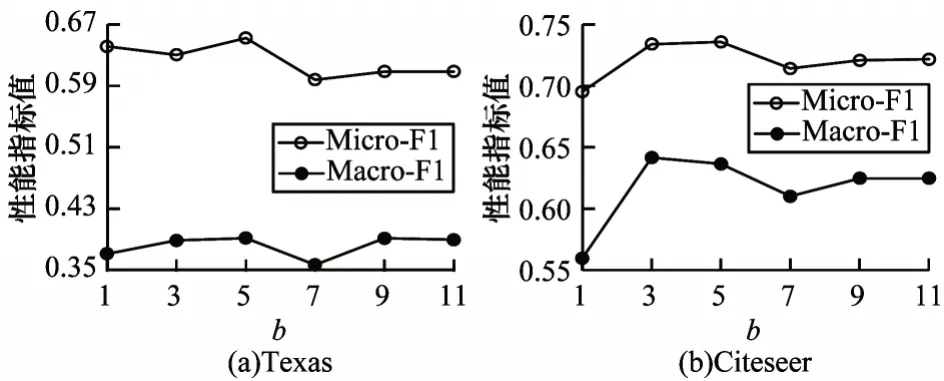
图8 参数b 分析 Fig.8 Analysis of the parameter b

参数ε用于控制损失函数中局部约束的比重，图9给出了不同ε值的实验结果。ε值越大，模型越关注一阶相似度信息，但是较大的ε值不会带来较好的分类性能。由图9 可以看出，在Texas 和Citeseer 数据集上，当ε=10-2时，模型获得最佳性能。上述结果表明，虽然局部约束能够保留原始图的重要信息，但是过高的比重会降低模型的表示能力，因此需要通过参数ε平衡损失函数中的局部损失比重。

图9 参数ε 分析 Fig.9 Analysis of the parameter ε

参数d用于控制生成嵌入的维度，图10 给出了不同d值的实验结果。Micro-F1 和Macro-F1 在开始时随维度的增加而提高，这是因为更多的维度使嵌入中编码了更多有益信息，提升了实验表现。但是，随着维度不断增加，Micro-F1 和Macro-F1 开始下降，这是因为过大的维度使嵌入中编码了噪声信息，降低了实验表现。因此，在生成节点嵌入时需要选择合适的维度，以获取模型的最佳性能。

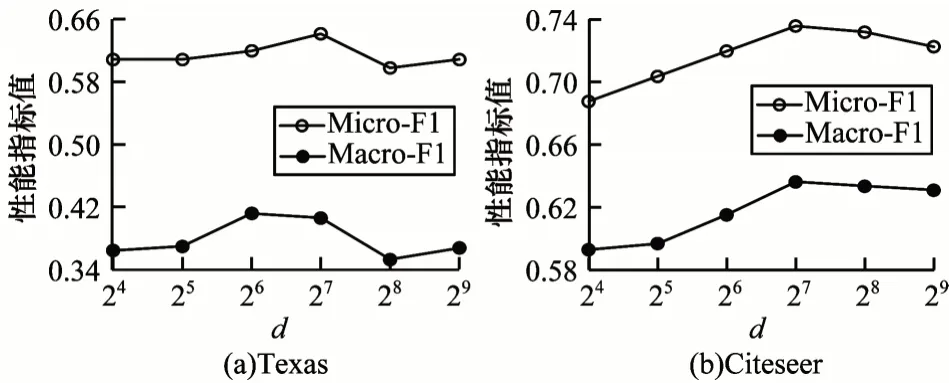
图10 参数d 分析 Fig.10 Analysis of the parameter d

3.6 训练时间对比

为了比较不同模型的训练时间，记录Cora 数据集上迭代100 次后单次迭代的平均训练时间（包括前向传播、损失函数计算和反向传播），实验结果如图11 所示。由图11 可以看出：GALA 由于仅使用GCN 编码器和重构损失，计算速度最快；DANE 使用简单的线性编码器进行编码，利用重构损失、一阶损失和高阶损失进行优化，因此训练时间比GALA 更长；GATE 在每次迭代中都需要计算节点间的注意力系数，同时使用重构损失和局部约束进行优化，使得训练时间较长；MC-GCAE 使用4 组GCN 编码器，同时利用重构损失、局部约束和一致性约束进行优化，导致训练时间长于结构和优化方式更简单的GALA。

图11 训练时间对比Fig.11 Comparison of the training times

4 结束语

为提升传统GCN 编码器模型对于属性和拓扑信息的融合能力，本文提出基于多通道图卷积自编码器的图表示学习模型MC-GCAE，充分保留了原始图的属性、拓扑以及两者关联信息。实验结果表明，多通道图卷积编码器生成的融合嵌入表示能够提升节点分类、节点聚类、可视化等图机器学习任务的性能表现。此外，通过组件性能分析可以看出，多通道融合模型相较使用单一特征空间的组件能够更好地泛化到不同类型的图数据集上。在当前工作中，使用局部约束保留了图的一阶相似度信息，但未保留二阶相似度、社群特征等高阶相似度信息。因此，在后续工作中，将对图的低阶信息、高阶信息及两者关联信息进行分析和挖掘，使生成嵌入中能够保留更丰富的原始图信息。