基于改进PPO 算法的机器人局部路径规划

刘国名，李彩虹，李永迪，张国胜，张耀玉，高腾腾

（山东理工大学 计算机科学与技术学院，山东 淄博 255000）

0 概述

路径规划是机器人领域的重要组成部分，主要分为全局路径规划和局部路径规划［1］。全局路径规划是从整体环境出发，依据已知地图信息规划出一条从起点到目标位置的安全无碰撞路径；而局部路径规划是在未知环境下，通过雷达传感器探测周围环境信息来进行路径规划［2-3］。常用的局部路径规划方法有人工势场［4］、模糊控制［5］、神经网络［6］、强化学习［7］等。其中，强化学习不需要任何先验知识，其通过机器人与环境交互、累积奖励来优化策略；而神经网络能够解决传统强化学习算法无法处理的高维连续状态和连续动作信息，可以很好地对机器人避障问题进行建模［8-9］。随着深度学习、神经网络以及计算能力的提升，深度学习和强化学习结合的深度强化学习已经成为目前机器人路径规划研究的热点［10］。

强化学习方法主要分为基于值函数的方法和基于策略梯度的方法［11］。传统强化学习通常使用基于值函数的方法，如CHRISTOPHER等［12］提出的通过Q 值表来对不同状态进行打分，但该方法需要大量资源来维护Q 值表，当状态和动作空间高维连续时，Q 值表无法完成存储。Google Deepmind 团队提出深度强化Q 学习（Deep Q-Learning，DQN）算法［13］，利用神经网络把Q 值表的更新问题变成一个函数拟合问题；随后又证明了确定性策略梯度（Deterministic Policy Gradient，DPG），提出深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）算法实现了连续动作的学习，该算法更接近于基于值函数的方法［14］。与基于值函数的方法不同，基于策略梯度的方法是模型直接输出具体动作，并通过环境反馈利用梯度上升来直接修改策略参数［11］。WILLIAMS等［15］提出的Reinforce 算法，通过蒙特卡洛采样来更新策略所需梯度，但算法中指导更新方向的状态价值通过回溯方法获得，采样效率较低。SCHULMAN等［16］提出置信域策略优化（Trust Region Policy Optimization，TRPO）方法限制输出域更新范围，但影响了算法的实现效率和更新速度。OPENAI 团队提出近端策略优化（Proximal Policy Optimization，PPO）算法，实现了更简洁的一阶更新限制幅度方法［17］。PPO 算法对于连续控制问题有很好的表现，其以马尔可夫决策过程（Markov Decision Process，MDP）为基础，延续了置信域策略优化算法的步长选择机制，借鉴了基于策略的估计思想以及Actor-Critic 框架中策略与价值双网络的经验［18］。申怡等［19］提出基于自指导动作的SDAS-PPO 算法，利用增加的同步更新经验池提高了样本的利用率，但该方法在训练过程中容易产生梯度爆炸的问题。对于机器人路径规划任务，通过深度强化学习算法收集到的数据具有时序性且环境状态存在相关性，而神经网络可以通过强大的表征能力来解决连续状态动作空间问题。长短期记忆（Long Short-Term Memory，LSTM）神经网络是一种特殊的循环神经网络，能够解决长序列训练过程中的梯度消失和梯度爆炸问题，因此，LSTM 神经网络能够很好地满足任务需要［20］。

PPO 算法能够解决连续动作和高维连续状态的问题，但存在收敛速度慢、易陷入死锁区域等不足［21］。本文对PPO 算法进行改进，引入LSTM 神经网络，将机器人6 个雷达传感器探测的信息以及机器人与目标点之间的距离和夹角作为网络输入，将机器人的角速度和线速度作为网络输出，记忆奖励值高的样本，遗忘奖励值低的样本；在训练过程中，通过判断机器人所处状态决定是否启用虚拟目标点，帮助机器人走出陷阱区域，从而减少模型学习时间，提高算法收敛速度。

1 状态、动作空间和奖惩函数的设计

本文设计合理的状态、动作空间以及奖惩函数，利用传感器探测并收集环境信息，然后将数据信息作为状态特征向量输入到网络中，根据策略选择最优动作、获取奖励，通过累积奖励来优化策略。

本文采用两轮差分驱动机器人作为仿真测试平台［22］，利用全方位激光雷达传感器检测环境信息。雷达传感器探测范围设置如图1 所示。

图1 雷达传感器探测范围Fig.1 Radar sensor detection range

在图1中，扇形区域代表传感器180°探测范围，每5°返回一组该区域内距离机器人最近障碍物的距离信息，共测得36 组数据。把测得的36 组数据相邻分为6组，每组6 个数据，将每组数据信息经特征融合之后作为该30°区域传感器测得的信息。

机器人的状态空间由8 个特征向量组成，分别为6 个方向传感器返回的最近障碍物的距离信息di（i=1～6）、机器人与目标点之间的距离信息Dr和机器人运行方向与目标点方向之间的夹角θr。状态空间s定义为：

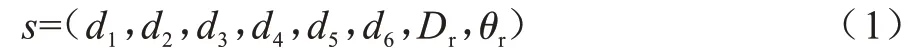
动作空间包括角速度ωr和线速度vr。参考机器人运动学并考虑实际需求，对角速度ωr和线速度vr的范围进行归一化，机器人角速度ωr∈［-1，1］，线速度vr∈［0，1］［23］。动作空间a定义为：

奖励函数是决定强化学习算法能否成功收敛的关键［24］。本文设计的奖励函数R主要由三部分组成，分别为距离奖惩R1、方向奖惩R2和累加转角和奖惩R3。R1和R2表示机器人执行动作之后，如果距离目标点更近或者与目标点之间的夹角更小，则给予适当奖励，反之则给予惩罚；考虑到机器人前期可能会频繁转弯导致训练过程中不必要的训练，添加执行n次动作后的累加转角和奖惩R3，超过阈值则给予惩罚。奖励函数设计如下：

其中：r1表示机器人到达目标点获得的奖励；r2表示机器人碰到障碍物获得的惩罚；Db表示机器人未执行动作前与目标点之间的距离；Dr表示机器人当前状态与目标点之间的距离；θb表示机器人未执行动作前与目标点连线之间的夹角；θr表示机器人当前状态运行方向与目标点连线之间的夹角；θs表示机器人连续执行动作后的累加转角和。

2 改进PPO 算法

为加快算法收敛速度并解决训练过程中易陷入死锁区域的问题，本文对PPO 算法进行改进：将与环境交互收集到的相关性样本信息作为特征向量输入到LSTM 神经网络中，利用LSTM 神经网络中的记忆单元选择样本中需要记忆和遗忘的信息，基于PPO 算法选择最优动作并获取奖励优化策略；同时在陷入死锁区域时启用虚拟目标点，在不同场景中设置不同位置的虚拟目标点，引导机器人走出各种死锁区域。

2.1 PPO 优化策略

PPO 算法的原理是将策略参数化，即πθ（a|s），利用参数化的线性函数或者神经网络来表示策略。PPO 算法框架如图2 所示。

图2 PPO 算法框架Fig.2 PPO algorithm framework

PPO 策略梯度算法通过计算估计量结合随机梯度上升算法来实现，更新公式为：

其中：θb为更新前的策略参数；θr为更新后的策略参数；α为学习率；∇θ为重要性权重；J为优化目标，即在状态s下未来奖励的期望值［25］。

策略梯度算法存在难以确定更新步长的问题，当更新步长不合适时，更新后的参数对应的策略回报函数值会降低，越学越差导致算法最终无法收敛。通过式（5）将新旧策略网络的动作输出概率的变化范围r（θ）限制在一定区域内，可以解决此问题，这也是PPO 算法的核心。

其中：CLIP 是python 中的函数，是指取区间；ε为超参数，一般设置为0.2；为优势函数；Q（sr，ar）为在状态sr下采取动作ar的累积奖励值；V（sr，ar）为状态估计值。当>0时，说明此动作比平均动作要好，增大选择该动作的概率；当<0时，说明此动作比平均动作要差，减少选择此动作的概率。但是网络得到的动作的概率分布不能差太远，因此，分别在1+ε和1-ε处截断，限制策略更新的幅度。图3（a）和图3（b）分别说明了这两种情况。

图3 目标函数的限制范围Fig.3 Restricted range of objective function

2.2 LSTM 神经网络结构

LSTM 神经网络之所以能够在应对长序列问题时有很好的表现，主要是其在神经网络结构中引入了门控概念，通过计算遗忘门、输入门和输出门的状态信息来控制记忆单元［26］。LSTM 神经网络结构如图4 所示。其中：t表示当前时刻；xt表示当前输入；ht-1表示上一时刻输出；ht表示当前输出；ct-1表示上一时刻单元状态信息；ct表示当前单元状态信息；σ表示sigmoid 函数，输出为0～1 之间的数字，表示一个神经元有多少信息可以通过；tanh 表示双曲正切层。

图4 LSTM 神经网络结构Fig.4 LSTM neural network structure

当有新的状态输入到达之后，ht-1和xt通过遗忘门层中的sigmoid 函数决定在神经元细胞中遗忘什么信息，输出为0～1 之间的数字，“1”代表“完全保留”，“0”代表“完全遗忘”，计算公式如下：

下一步决定在神经元细胞中保存的信息，包括两部分：一部分是通过输入门层中的sigmoid 函数决定的更新数值it；另一部分是通过tanh 层生成的新候选数值。

将这两部分信息添加到神经元状态中，可得到当前时刻状态信息ct，如式（9）所示：

通过输出门层中的sigmoid 函数决定输出的神经元状态，记为ot。将当前时刻状态信息ct通过tanh函数归一化到-1～1 之间，两者相乘得到当前时刻输出值ht，计算公式如下：

2.3 LSTM-PPO 网络结构

根据机器人局部路径规划任务的需求以及雷达传感器的数据信息，本文将LSTM-PPO 网络设计为8 输入、2 输出结构。以机器人运动轨迹的状态信息作为输入，当前时刻机器人采取的动作作为输出，每一次执行动作后获得奖励值，通过策略梯度更新网络参数以及自适应优化算法训练得到最终模型。LSTM-PPO 网络结构如图5 所示。

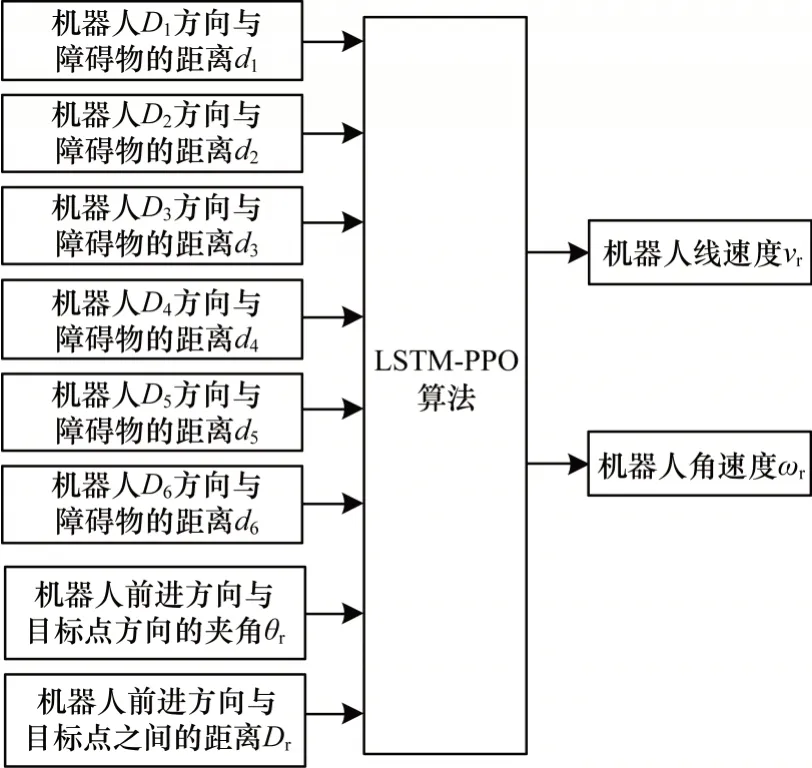
图5 LSTM-PPO 网络结构Fig.5 LSTM-PPO network structure

LSTM-PPO 网络主要包含4 层神经网络，如图6所示。第1、2 层为全连接层，分别包含128 和64 个隐藏神经元节点，将机器人的状态信息序列作为输入的特征向量，使用ReLU 非线性函数作为激活函数，进行更好的特征提取；第3 层为LSTM 神经网络层，包含3 个隐含的LSTM 记忆单元，用于获取一系列时间序列上的记忆信息，控制之前状态信息和当前状态信息的遗忘和记忆程度；第4 层为全连接层，输出策略均值μ和策略方差σ，分别利用sigmoid 函数和tanh 函数作为激活函数，通过高斯分布N=（μ，σ）采样，获得机器人运动的线速度vr和角速度ωr。

图6 LSTM-PPO 神经网络结构Fig.6 LSTM-PPO neural network structure

2.4 虚拟目标点设计

与离散障碍物场景不同，在特殊障碍物场景中，存在着死锁状态，机器人在学习趋向目标点的过程中，会频繁碰到“一”型和“U”型场景中的障碍物，导致难以走出死锁区域。本文通过设计虚拟目标点来帮助机器人学习绕过特殊障碍物环境趋向目标点的经验，解决远离目标点奖励值减小的问题。在判断机器人进入特殊障碍物场景中的死锁状态后，弃用目标点，启动虚拟目标点，利用虚拟目标点引导机器人；在判断走出死锁区域之后，弃用虚拟目标点，重新启用目标点，给予机器人正确的引导。

将传感器Di（i=1～6）方向存在障碍物设为状态“1”，无障碍物设为“0”，虚拟目标点设置的距离Dv设为传感器探测距离100 cm。通过读取机器人6 个传感器返回的障碍物数据信息，判断机器人是否进入死锁状态，如果已进入，读取当前机器人与目标点之间的夹角θr，利用表1 设计的虚拟目标点规则计算出当前虚拟目标点设置的方向θv，尽可能远离障碍物。虚拟目标点的位置坐标（x1，y1）为：

表1 虚拟目标点规则 Table 1 Virtual target point rules

其中：（x，y）为机器人当前位置坐标。

图7 为虚拟目标点位置示意图（彩色效果见《计算机工程》官网HTML版，下同）。在图7（a）中，机器人处于“U”型场景中的陷阱区域内，此时雷达传感器探测到运行前方出现障碍物，根据表1 中虚拟目标点规则，将虚拟目标点设置在机器人运行方向的左前方向，引导机器人左转，减少碰到障碍物的概率；在图7（b）中，机器人左转后，雷达传感器在D3、D4、D5、D6方向探测到障碍物，继续在运行方向左前方设置虚拟目标点，解决远离目标点获得奖励减少的问题；在图7（c）中，机器人在走出死锁区域之后，需要在其右前方设置虚拟目标点，引导机器人绕过障碍物，否则会因为目标点的引导重新进入死锁区域。

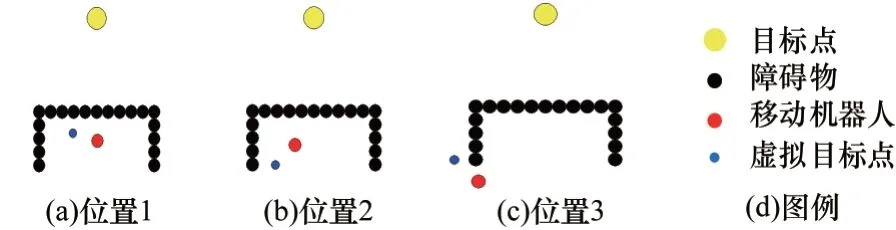
图7 虚拟目标点位置示意图Fig.7 Schematic diagram of virtual target point position

3 仿真与结果分析

3.1 算法验证与分析

本文在离散障碍物场景和特殊障碍物场景下进行模型训练，将传统PPO 算法、SDAS-PPO 算法作为对比算法。仿真环境为二维，大小设置为700 cm×700 cm。以黑色实线表示利用训练好的模型规划出的路径，其他符号意义同图7（d）中的图例所示。

3.1.1 离散障碍物场景

在离散障碍物场景下，通过初始化LSTM-PPO算法的参数，随机设置起始点、目标点和障碍物位置来构建随机环境，使机器人能够学习到趋向目标点和避障的经验。模型训练参数如表2 所示。

表2 离散障碍物场景的训练参数 Table 2 Training parameters under discrete obstacle scene

分别记录训练过程中机器人每一轮获得的平均奖励和每一次到达目标点的路径长度，如图8 和图9所示。由图8 可以看出：随着迭代轮数的增加，在LSTM-PPO 算法迭代到50 轮左右时，平均奖励已经从负值提升至0，说明算法已经学习到部分避障经验；当算法迭代到第80 轮时，每轮的平均奖励基本在0.02～0.04 之间波动且波动很小。由图9 可以看出：在机器人初次到达目标点后，路径长度下降迅速；在到达目标点100 次后，路径长度基本趋于稳定并维持在80 步上下波动，说明LSTM-PPO 算法基本趋于收敛状态。

图8 平均奖励（离散障碍物场景）Fig.8 Average reward（discrete obstacle scene）

图9 路径长度（离散障碍物场景）Fig.9 Path length（discrete obstacle scene）

图10 为利用LSTM-PPO 算法在2 种离散场景下训练模型规划的路径，可以看出，模型已学习到趋向目标点和避障的经验，路径平滑度较高且模型泛化能力强。

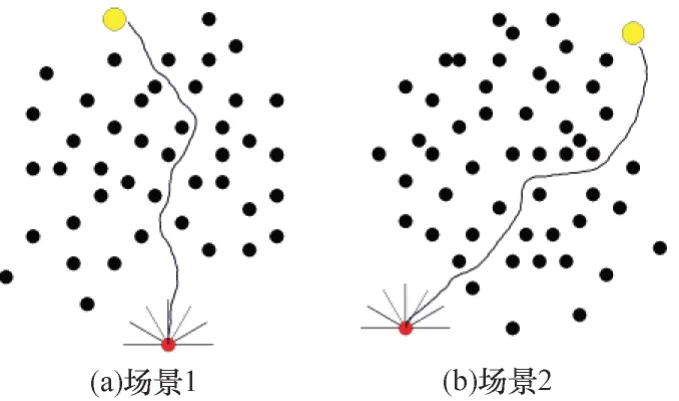
图10 规划路径（离散障碍物场景）Fig.10 Planning path（discrete obstacle scene）

3.1.2 特殊障碍物场景

特殊障碍物场景包括“一”型和“U”型场景，存在的问题主要是陷入死锁状态导致目标点不可达，因此，通过设计虚拟目标点来引导机器人走出死锁区域，减少在死锁环境中训练的时间，加快模型收敛速度。

图11 和图12 分别为在特殊障碍物场景训练过程中机器人每一轮获得的平均奖励和每一次到达目标点的路径长度。由图11 可以看出：机器人在特殊障碍物场景中获得的平均奖励在前50 轮处于负值，说明还未学习到足够走出死锁区域的经验；随着训练轮数的增加，每轮获得的平均奖励呈上升趋势，且在150 轮时达到峰值。由图12 可以看出：通过虚拟目标点的引导，在机器人第一次到达目标点之后，通过训练模型，规划路径的长度一直处于减小的状态且在训练后期趋于稳定，在训练期间，虚拟目标点的引导使机器人学习到了走出陷阱区域的经验，且具有足够的稳定性，说明算法已收敛。

图11 平均奖励（特殊障碍物场景）Fig.11 Average reward（special obstacle scene）

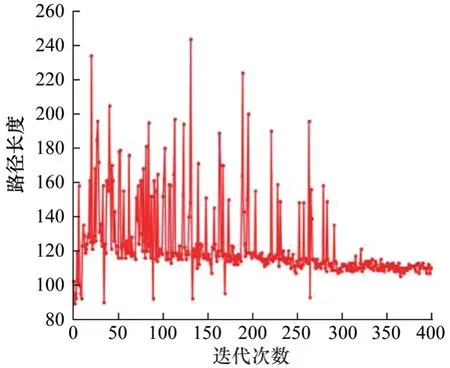
图12 路径长度（特殊障碍物场景）Fig.12 Path length（special obstacle scene）

图13 为机器人分别在“一”型和“U”型场景中规划出的路径。可以看出，通过虚拟目标点的引导训练出的模型，可以在雷达传感器探测到特殊障碍物状态时绕过死锁区域，在不碰到障碍物的同时规划出一条较短的路线。

图13 规划路径（特殊障碍物场景）Fig.13 Planning path（special obstacle scene）

3.2 对比实验

针对特殊障碍物场景和混合障碍物场景，分别基于传统PPO 算法、SDAS-PPO 算法和所提出的LSTM-PPO 算法实现机器人的局部路径规划任务，对比在相同场景下获得的平均奖励和路径规划长度。

图14 和图15 分别为“U”型障碍物环境下传统PPO算法、SDAS-PPO 算法和LSTM-PPO 算法所获得的平均奖励和规划路径长度对比。可以看出：LSTM-PPO 算法相对于传统PPO 算法和SDAS-PPO算法在前期训练过程中波动较小，且借助LSTM 神经网络的记忆功能，在虚拟目标点的引导下累积奖励更快，机器人能够更快找到目标点；在训练后期，规划的路径长度基本无波动，模型稳定性强，说明LSTM-PPO 算法能够使模型更快地到达收敛状态且具备更高的泛化能力。

图14 3 种算法的平均奖励对比（特殊障碍物场景）Fig.14 Average reward comparison of three algorithms（special obstacle scene）

图15 3 种算法的路径长度对比（特殊障碍物场景）Fig.15 Path length comparison of three algorithms（special obstacle scene）

图16 给出了3 种特殊障碍物场景下3 种算法的规划路径对比，其中，传统PPO 算法规划路径为红色实线，SDAS-PPO 算法规划路径为橙色实线，LSTMPPO 算法规划路径为黑色实线。显然，传统PPO 算法规划出的路径掺杂了太多冗余路段，而本文提出的虚拟目标点法可以很好地帮助机器人走出死锁区域，减少规划路径过程中出现的冗余路段，大幅缩短了路径长度。3 种算法路径长度对比如表3 所示。

图16 3 种算法的规划路径对比（特殊障碍物场景）Fig.16 Planning path comparison of three algorithms（special obstacle scene）

表3 3 种算法的路径长度对比（特殊障碍物场景）Table 3 Path length comparison of three algorithms（special obstacle scene）

图17 和图18 分别为混合障碍物场景下3 种算法所获得的平均奖励和规划路径长度对比。可以看出，3 种算法在收敛后所获得平均奖励都能达到峰值且规划路径长度基本相同，但LSTM-PPO 收敛速度相对较快，且每轮奖励以及路径规划长度更加稳定，波动较小，说明LSTM-PPO 算法训练出的模型鲁棒性更好，泛化能力更强。

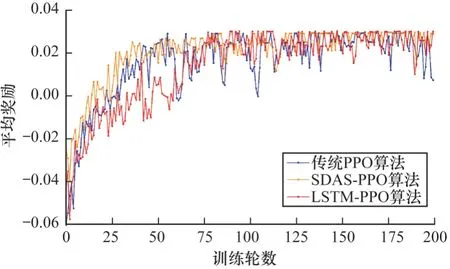
图17 3 种算法的平均奖励对比（混合障碍物场景）Fig.17 Average reward comparison of three algorithms（mixed obstacle scene）

图18 3 种算法的路径长度对比（混合障碍物场景）Fig.18 Path length comparison of three algorithms（mixed obstacle scene）

图19 给出了混合障碍物场景中3 种算法的规划路线对比图。可以看出，LSTM-PPO 模型规划出的路径平滑度更高，转弯角度更小且长度更短。3 种算法的路径长度对比如表4 所示。

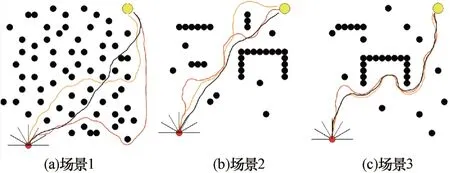
图19 3 种算法的规划路径对比（混合障碍物场景）Fig.19 Planning path comparison of three algorithms（mixed obstacle scene）

表4 3 种算法的路径长度对比（混合障碍物场景）Table 4 Path length comparison of three algorithms（mixed obstacle scene）

4 结束语

本文对PPO 算法进行改进，提出基于PPO 算法和LSTM 神经网络的LSTM-PPO 算法，并在特殊障碍物场景下引入虚拟目标点，与传统PPO 算法和SDAS-PPO算法在各场景中进行仿真对比。LSTM-PPO算法引入了具有记忆功能的LSTM 神经网络，能够加快模型的收敛速度，使训练好的模型具有更强的泛化能力，同时其利用直接搜索策略更新参数，能够处理连续动作和高维连续状态，有更好的收敛性以及更强的鲁棒性。设计的虚拟目标点法能够在陷入死锁区域时启用虚拟目标点来引导机器人走出陷阱，解决特殊障碍物场景下容易陷入死锁状态造成目标不可达的问题。本文假设的障碍物位置固定且通过传感器获取的障碍物信息是没有偏差的，下一步将对所提算法进行改进，使其适用于障碍物数目更多以及存在动态障碍物的实际应用场景。