Anomalous diffusion in branched elliptical structure

Kheder Suleiman, Xuelan Zhang(张雪岚), Erhui Wang(王二辉),Shengna Liu(刘圣娜), and Liancun Zheng(郑连存),†

1School of Energy and Environmental Engineering,University of Science and Technology Beijing,Beijing 100083,China

2School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China

Keywords: anomalous diffusion,Fokker–Planck equation,branched elliptical structure

1. Introduction

Diffusion is an essential means of transportation in biological, physical, and chemical systems that is used by individuals to achieve their functions, for example, but not limited to, cellular processes, metabolism, and conduction.[1–5]Realizing the features of diffusion, which depend on its microscopic dynamics and environmental space,will provide an important tool to control these processes, besides its possible applications in nanotechnology and nanomedicine. According to the theory of Brownian motion,the probability distribution is Gaussian and mean square displacement(MSD)of the particle position grows linearly with time〈r2(t)〉=2DtwhereDis the diffusion coefficient. However, deviations from these usual behaviors have been observed theoretically and experimentally, anomalous (non-Brownian) diffusion,[6–10]Brownian yet non-Gaussian diffusion,[11–13]and anomalous yet non-Gaussian diffusion.[14,15]The nonlinear dependence of time characterizes the MSD in the anomalous dynamics, namely,〈r2(t)〉]～tαwithα/=1. The diffusion dynamics with transport exponent 0＜α ＜1 correspond to sub-diffusion dynamics which are observed in artificially crowded liquids,[16]lipid bilayer membranes,[15,17]the cytoplasm of biological cells,[18]extracellular space,[19]and in hydrology,[20]to mention a few.Whereas,it defines super-diffusion whenα ＞1,which is encountered in active systems such as molecular motor transport in cells.[21,22]Different hypotheses have been suggested to understand the mechanism underlying sub-diffusion dynamics, which depends on the situation at hand, among them,trapping models of energetic (binding sites) or geometric nature,labyrinthine environment(geometrical disorder),temporal correlation due to slow mode(viscoelastic environments),space-dependent diffusivity due to the local porosity of the medium or temperature field in the sense of weak gradients,which can be modelled by continuous time random walk(CTRW), random walk on fractals, fractional Brownian motion (FBM) or fractional Langevin equation (FLE), and heterogeneous diffusion process(HDP),respectively.[8,23–27]

Disordered materials in nature are abundant, including to mention a few the heterogeneous porous media, extracellular space in brain tissue, intra-tissue in muscles, cell cytoplasm, and glasses.[28–35]Diffusion in disordered media is quite affected by its geometrical structure, for instance, dead ends, bottlenecks, and backends. Since deterministic fractals and percolation clusters are elegant models for the geometrical structure of disorder systems, Pierre-Gilles de Gennes has suggested modelling diffusion in these systems through performing random walks on percolation clusters and fractals,and coined the term“ant in the labyrinth”.[26]Random walks in these structures lead to anomalous diffusion. At the percolation threshold, a percolation structure can be idealized as a single infinite cluster, consisting of a conducting path, which corresponds to a backbone,and side branches,or fingers with dangling bonds. At some level of idealization, this structure corresponds to a comb.[36]Later,the comb-like structure consisting of the one-dimensional axis (backbone) with perpendicular sides branches (fingers) has been used to understand the underlying mechanism of anomalous diffusion in percolation clusters: while the particle moving randomly along the backbone may trap inside the dead-ends(fingers),performing a Brownian motion,until it returns by chance to the backbone where it can escape from the finger. Along they-direction(the so-called fingers),the particles perform normal diffusion,while the mean square displacement (MSD) along the backbone grows non-linearly with a time〈x2(t)〉≃and subdiffusion behavior dominates the process.[26,37,38]

To study the transport properties of diffusion process on comb-like structure, different approaches have been applied, e.g., a mesoscopic approach used by Weiss and Havlin,[37]a macroscopic approach used by Arkhincheev and Baskin,[39]and a microscopic approach used by M´endezet al.[40]Arkhincheev and Baskin have expressed the diffusion process in the comb by using the following Fokker–Planck equation:[39]

Here,Dx=δ(y) ˜DandDy=Dare the diffusion coefficients in thexandydirections, respectively, and theδ-function in the Fokker–Planck operatorLFP=δ(y)+means that the diffusion along thexdirection(the so called backbone)is allowed only aty=0.

Recently, comb-like model has been used to describe anomalous diffusion in spiny dendrites,[41]the mechanism of super-diffusion of ultracold atoms in a one-dimensional as a phenomenology of experimental study,[42]as well as anomalous diffusion in porous materials.[43]Moreover, several complex extensions of comb-like structure, through introducing a modification on the geometry of the backbone or finger shape of the structure, is introduced to describe geometrically induced complex diffusion in nature, for example, comb with a finite finger length,[40,44,45]cylindrical comb,[46,47]random comb models,[48,49]comb with ramified teeth,[40,41]fractal mesh and grid structures,[50–52]and more complex structure.[53–57]Diffusion along the backbone in both two and three-dimensional comb-like structures with a finite finger is a transient sub-diffusion followed by normal diffusion at long times, and the same result is obtained in using a trap model of energetic nature.[58]Whereas, diffusion along the backbone in a three-dimensional comb-like structure with an infinite two-dimensional branch is ultra-slow diffusion/enhanced sub-diffusion if normal/sub-diffusion occurs inside branches.[46,47]In addition,recent theoretical studies have been demonstrating that performing different microscopic dynamics in a comb-like model leads to different types of anomalous diffusion.[59–63]In most previous studies, the geometric properties of the backbone have not been considered. However, the interior of disordered systems are narrow, tortuous,curved channels.[26,64,65]

In the last decade, the problem of diffusion in curved confined tubes has attracted remarkable attention of some researchers, as it was found that the behavior of the diffusion process is affected by its geometrical properties, like curvature and torsion,of these tubes.[66–69]This problem is related to diverse kinds of phenomena, for example not limited to,diffusion of biomolecules in biological cell,[70]transport of solute in aquifers and porous medium,and fluxon dynamics in Josephson junction.[71]The aim of this paper is to study the diffusive dynamics in branched channels with gradient curvature. Branched elliptical-like channels are common in biology,including to mention a few,the extracellular spaces in the biological tissues(brain,tumors,muscles),intracellular environments, and other porous media,[19,31,72–78]in which diffusion process in these structures are important for other biological processes like extracellular ionic buffering, and delivery of drugs and metabolites,etc.[79,80]Moreover,they are simple models of curved confined sub-diffusive systems with gradient curvature.Motivated by the foregoing,we analyze the dynamics of the diffusion process in an elliptical comb-like structure(see Fig. 1) with reflected boundary conditions. The elliptical motion takes place only for a fixed radiusr=Rand is interspersed with a radial motion inward and outward of the ellipse. The Brownian radial motion corresponds to diffusion of particles in dead-end spaces, while elliptical backbone describes the dynamics along elliptical channels. We investigate by numerical simulation how probability distribution function(PDF) and mean square displacement (MSD) are affected by geometrical constraints in the elliptical comb-like structure.

The rest of the paper is organized as follows. We firstly formulate the mathematical description of the problem in Section 2. The numerical method and example on the verification of the numerical algorithm are collected in Section 3. Then results and discussion are illustrated in Section 4. The conclusions are given in Section 5.

2. Mathematical formulation

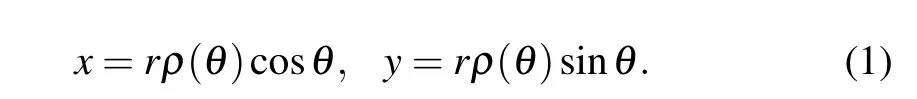
The structure we study here consists of elliptical channel with radii dead ends distributed along it and directed in/outside(see Fig. 1), in which an unbiased diffusion process occurs inside it. Mathematically, suppose an ellipse whose boundary has the polar equationρ(θ) =b/, where 0＜e ＜1 is the eccentricity of ellipse,bis the shortest diameter with constant value,andθ ∈[0,2π]. Then,its domain can be obtained through stretched radiusrsuch thatϒ=rρ(θ)withθ ∈[0,2π], andr ∈[0,1], where we can move from Cartesian coordinates to stretched polar coordinates through the transformation[81]The distinctive feature of diffusion process in such structure is that the particle motion alongθdirection is possible only whenr=RandRis a constant. We mean that the tangent diffusion coefficientDθis different from zero only atr=R,i.e.,Dθ= ˜Dδ(r-R)with ˜Dis a constant.Whereas,the diffusion is free in the radial direction situation and its diffusion coefficient can be written asDr=D. By adjusting the parameterethe elliptical channel(backbone)has different shapes,in which the curvature of the ellipse ,withdecreases as the value ofeincreases(see Fig. 1). In order to assess how particles diffuse in the structure probability distribution function(PDF)P(r,θ,t),marginal PDFP(r,t), and mean square displacement (MSD)alongθare a useful quantities. In the classical comb model,PDFP(r,θ,t)can be described by Fokker–Planck equation[39]∂tP=δ(y)P+P. Theδfunction in the Fokker–Planck operatorLFP=δ(y)+means that the diffusion along thexdirection is allowed only aty=0. In what follows, we derive the diffusion equation in a stretched polar coordinate system, then find the differential equation that expresses the diffusion process in our structure.

Fig.1. Schematic picture of an elliptical comb-like structure,where the radii are continuously distributed over the ellipse of radius R=ρ(θ)with θ ∈[0,2π].

2.1. Derivation of diffusion equation in stretched polar coordinates

The gradient operator can be written as follows:

Then,the balance equation and the first Fick’s law can be written respectively as follows:

Then the second Fick’s equation reads

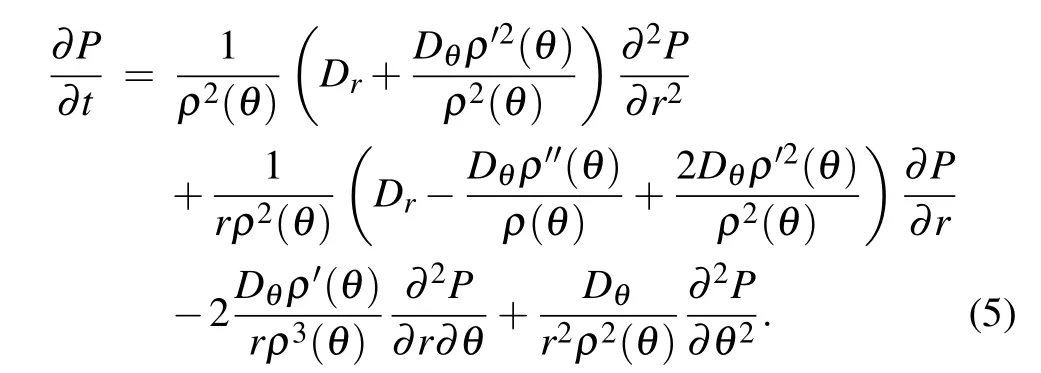
2.2. Diffusion equation in elliptical comb-like structure

with initial condition

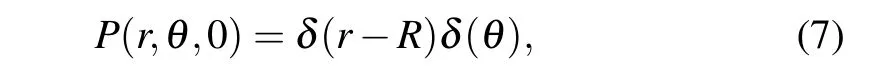
and boundary conditions

3. Numerical procedure

3.1. Numerical algorithm

The initial–boundary value problem(6)–(8)can be solved numerically by using the following procedure: Firstly, in order to divide the spatial and temporal domain into grid, we defnieri=ihr,θj=jhθ, andtl=lτwherei=j=, andl=besideshr=R′/Nr, andhθ=π/Nθare space steps,τ=T/NTis time step. Letbe the numerical solution of Eq.(6)at point(ri,θj,tl),then the first and second order derivatives in the governing equation can be discretized as follows:

Now, applying the previous approximate scheme to Eq. (6)yields the following iterative equations:

where

3.2. Verification of the validity of the numerical solution

In order to test the correctness of numerical solution,we introduce a source functionf(r,θ,t)in Eq.(6),and this yields the following equation:

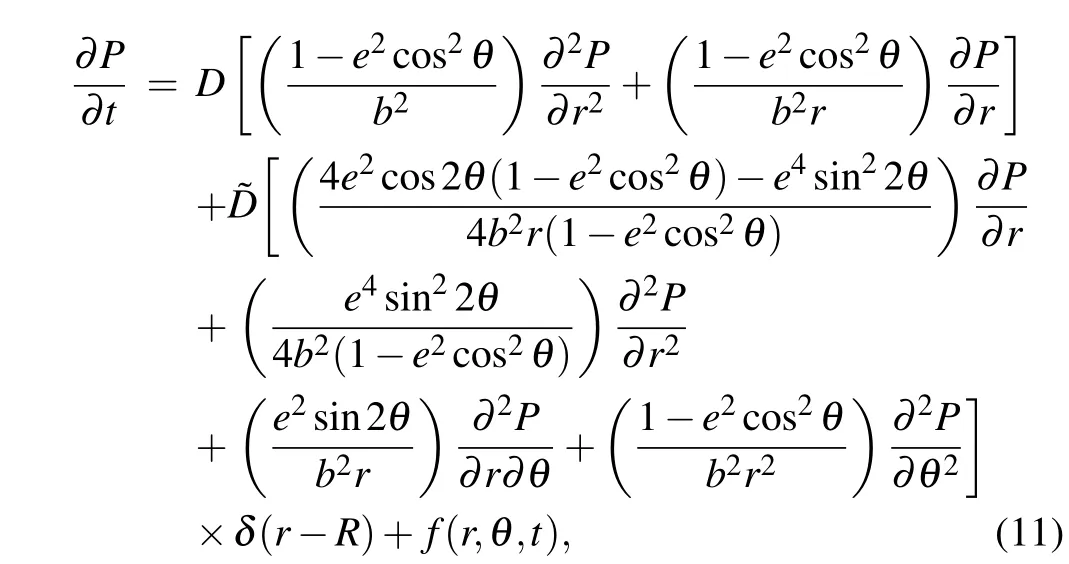
with initial condition

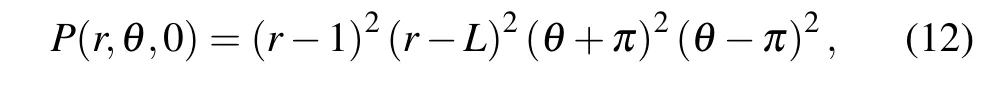
and boundary conditions

where

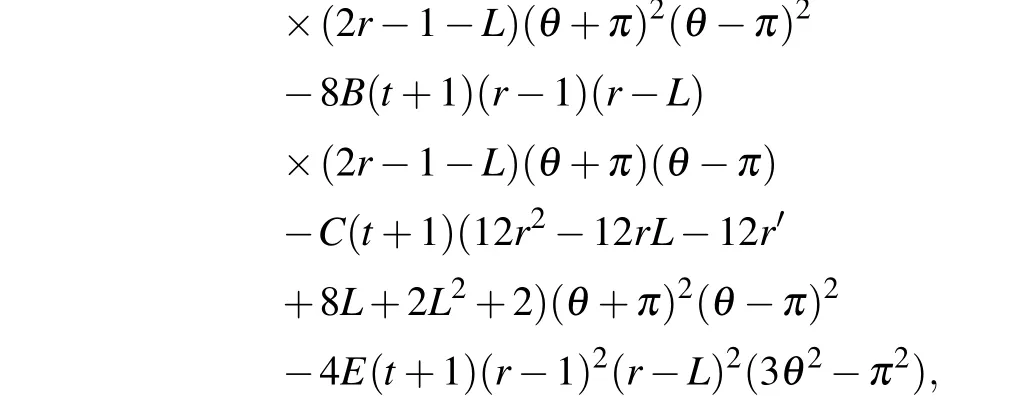
with

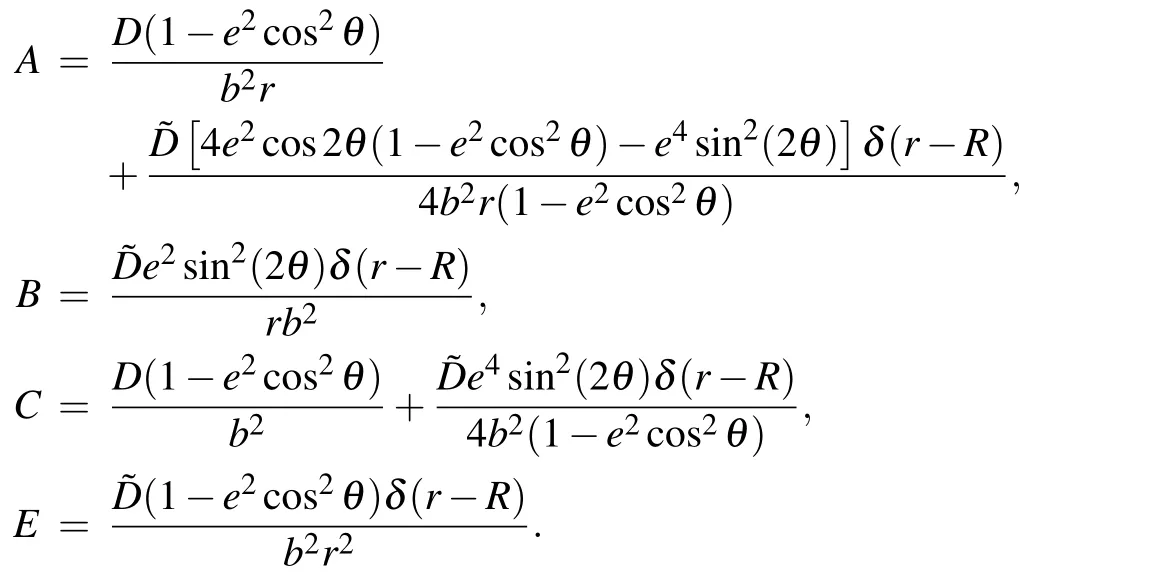
The exact solution of the equation is given by

The comparison between the exact and numerical solution of Eq. (13) subject to the initial condition and boundary conditions Eqs. (12)–(15) is shown in Fig. 2. We can see that the curves in a good agreement which indicates the correctness of numerical results.

Fig.2. The comparison of the exact solution via Eq.(16)with numerical solution for b=1, e=0.5, D= ˜D=1, τ =10-4, hr =10-2, and hθ =π/20 at T =1.

4. Results and discussion

4.1. Probability distribution function

The probability distribution function(PDF)P(x,y,t)is a useful quantity to assess how particles are distributed in the structure. In case of classical comb with a reflected boundary conditions, the evolution of PDFP(x,y,t) can be described by the comb equation∂tP(x,y,t)=δ(y-y0)P(x,y,t)+DP(x,y,t) with the following initial and boundary conditions:

The temporal evolution of marginal PDFP1(x,t) =P(x,y,t)dy, which characterizes the distribution of particle along the backbone,is detailed in Figs.3 and 4. Figure 3 shows that, for fixedL,P1(x,t) converges to the same non-Gaussian function(x,t)as time increases,and the speed of convergence is inversely proportional toR(the length of the lateral finger 2R). Moreover, the function(x,t) is affected byL, in which the concentration reduces as the length of the backbone increases, seen in Fig. 4. This means that the particles diffuse slowly, then they saturate after a period due to limited of the backbone. Moreover,the stay time in the branch until they return to the backbone determines the nature of its diffusion and reaches a saturated state. This will be demonstrated in the next subsection. Now, we show the effects of the parametersbandeon the distribution of particlesP(r,θ,t)in the whole elliptical comb-like structure, and the marginal PDF(θ,t)alongθdirection of the structure. The temporal evolution of the distribution in the structure is drawn from the iterative Eq.(9)by using Matlab. The parametersbandereflect the geometric properties of the ellipse.The relationship among the shortest diameterb, the longest diametera, and the eccentricity of ellipseereads asa2=b2/（1-e2）with 0≤e ＜1. Moreover, the curvature of an ellipse is given asFor fxiedb,the curvature of the ellipse decreases as the value ofeincreases. Figure 5 depicts the distribution of particles in the structure with different parameter effects atT=1. It shows that the concentration at the initial position increases as the shortest diameterband the eccentricityeof ellipse increases. Namely, the diffusion of particles slows down as the length of lateral branches and the curvature of the elliptical channel increase,in which these increments affect the waiting time and obstruction in the diffusion process.

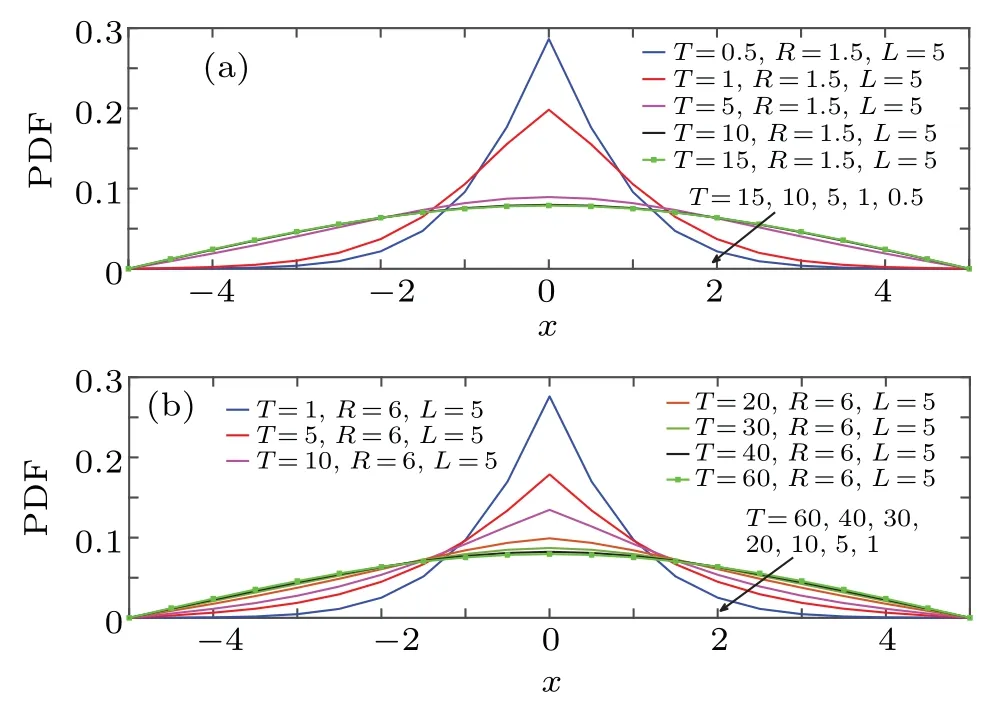
Fig.3. Time evolution of PDF in the backbone of classical comb,along x direction,for D= ˜D=1,L=5,and(a)R=1.5,(b)R=6.

Fig.4. Time evolution of PDF in the backbone of classical comb,along x direction,for D= ˜D=1,R=3,and(a)L=5,(b)L=10.

Fig.5. Time evolution of probability distribution in the structure for different value of the parameter b at T =1: (a)D= ˜D=1,e=0.5,and b=2,(b)D= ˜D=1,e=0.5,and b=3,(c)D= ˜D=1,e=0.5,and b=4,(d)D= ˜D=1,e=0.5,and b=5.

Figures 6 and 7 depict the temporal evolution of marginal PDF alongθdirection whenR=1/2,which show a symmetrical and non-Gaussian behavior according to different parameters. Figure 6 shows that the diffusion process slows down as the length of lateral branches increases, which can be attributed to the elapsed time in radial dead ends until the particle returns to the backbone. Besides, as in classical comb, it converges to a non-Gaussian function after a period that varies according to the length of the fingerb. However,unlike classical comb, this function also alters according tob. The effects of the eccentricity of elliptical channele, for fixedb,on marginal PDF alongθdirection are detailed in Fig. 7. It shows that the concentration at the initial position increases as the eccentricity increases. According to PDF quantity, the results can be summarized as following: The diffusion in a finite elliptical comb-like structure is abnormal and reaches a state of saturation after a period,which varies according to the stay time in lateral dead ends. Moreover, the concentration increases with the increase of the curvature of the elliptical channel,in which the increase of the curvature obstructs particle diffusion.

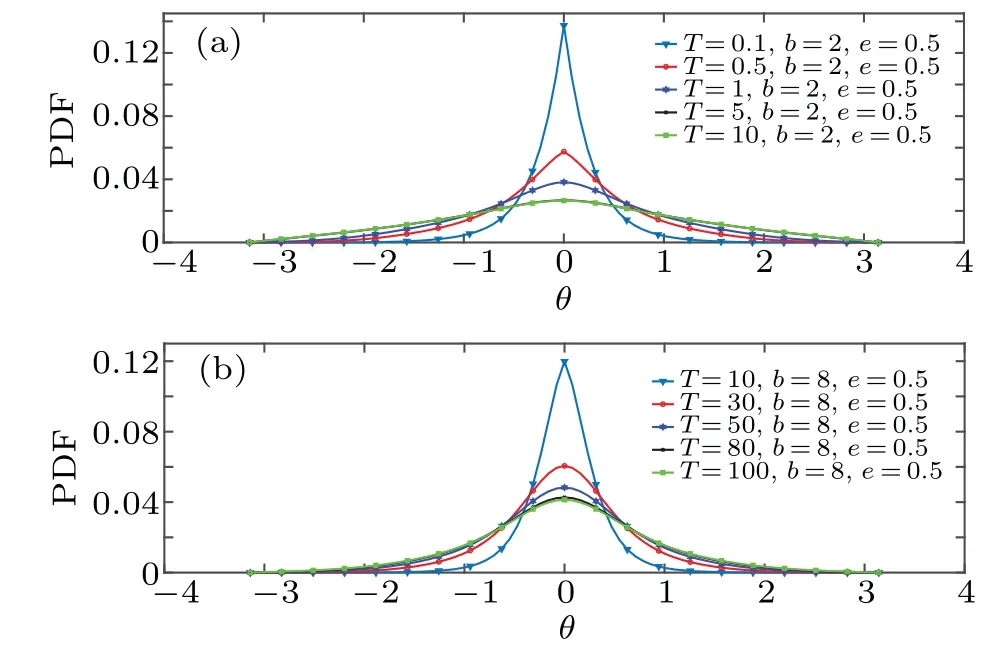
Fig.6. Time evolution of PDF in the backbone of elliptical comb,along direction θ,for D= ˜D=1,e=0.5,and(a)b=2,(b)b=8.

Fig.7. Time evolution of PDF in the backbone of elliptical comb,along direction θ,for D= ˜D=1,b=4,and(a)e=0.3,(b)e=0.8.

4.2. Mean square displacement

For more statistical information about this process and type of diffusion, the temporal evolution of the second moment (the mean square displacement (MSD) of the particle’s positions),which describes the speed of particle motion,in the backbone is calculated as

Firstly, we revisit MSD alongxdirection in finite classical comb with respect to parametersRandL. We use numerical simulation to obtain〈(x(t)-x0)2〉, in which we assumex0=0. As shown in Fig. 8, for fixedL,〈x2(t)〉grows nonlinearly for a short time, then it converges to a fixed value.However, the speed of convergence decreases asRincreases,which agrees with the results about PDF in the previous section. Besides,〈x2(t)〉～tαwithα ＜1 varies with respect toRand the transient sub-diffusion regimes dominate the process.Namely, one sub-diffusion regime will dominate the process asRtends to infinity. It should be noted that it has been established th〈atfor infniite comb model. The effects ofLonx2(t)is represented in Fig.9. It shows that the saturation threshold increases asLincreases. Namely, the state of saturation will go away whenLtends infinity. It should be mentioned that the saturation of the MSD is also found by considering diffusion in comb structures with stochastic resetting.[63,82]

Fig.8. Temporal evolution of MSD in the backbone of classical comb,along x direction for D= ˜D=1,R={1.5,3,6},and(a)L=5,(b)L=10.

Fig.9. Temporal evolution of MSD in the backbone of classical comb,along x direction for D= ˜D=1,L={5,7.5,10},and(a)R=1.5,(b)R=6.

Now, we consider the behavior of MSD alongθdirection in elliptical comb. As in the case of diffusion in classical comb, Fig. 10 shows a non-linear behavior of MSD alongθdirection,then it converges to constant value and the speed of convergence decreases asbincreases. However, for fixede,it does not converge to the same value, except in case of circle comb,i.e.,whene=0. Moreover,the saturating threshold is reduced aseincreases. This can be attributed to increase the perimeter of the elliptical channel,p ≈2πand the time of stay in the fingers. For short time, Fig. 10 shows that MSD～tαwith 0＜α ＜1, and a sub-diffusion process occurs in this direction. Besides, the value of exponentαdecreases aseincreases. Such transient sub-diffusion behavior was indeed demonstrated, for example, diffusion of fluorophore-labelled dextran (MW 3000) in granular layers(GL) of rat and turtle cerebella,[19]also diffusion in crowded media of non-inert obstacles.[83]

Fig.10. Temporal evolution of MSD in the backbone of classical comb,along θ direction for D= ˜D=1,b={2,4,5,6,8,10},and(a)e=0,(b)e=0.2,(c)e=0.5,(d)e=0.8.

Fig.11. MSD along θ direction for short time for D= ˜D=1, e={0,0.3,0.5,0.8},and(a)b=4,(b)b=7.

4.3. Diffusion in the elliptical channel without dead ends

The phenomenon of slow diffusion can be attributed here to the time the particles spend in the dead ends until they return to the backbone and the obstruction due to curvature of the ellipse. For more about the role of eccentricity or curvature of the ellipse, we consider the diffusion in the structure with the absence of dead ends. MSD along the elliptical channel is plotted in Fig. 12. In contrast to diffusion in elliptical comb,MSD grows linearly with time,and the diffusion is normal, see Fig. 12(a). However, MSD grows non-linearly with time as the curvature of the channel increases,see Fig.12(b),and sub-diffusion process is dominated.

Fig.12. MSD along elliptical channel without constrained geometries for short time for D= ˜D=1, and (a) e=0, 0.5, 0.8, and b=10, (b)e=0.5 and b=3,6,8.

5. Conclusion and perspectives

In this paper,we have considered the features of diffusion process in an elliptical channel with dead ends and discussed the impact of geometry of the structure on this process. To manipulate this problem, a modification of comb-like model has been suggested,in which the backbone and fingers of the comb correspond to the elliptical channel and radial dead ends distributed along it,respectively. The Fokker–Planck equation that expresses the diffusion process in the structure process has been derived and solved numerically. The results show a transient sub-diffusion behavior dominates the process followed by a saturating state. The sub-diffusion regime and saturation threshold are affected by the length of the elliptical channel lateral branch and its curvature. Besides,the concentration of particles at the initial position increases with the increase in the curvature of the elliptical channel. These established results can be added to the results of previous works that refer to the effects of curvature on diffusion processes in curved channels.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant Nos.11772046 and 81870345).