Enhancement of charging performance of quantum battery via quantum coherence of bath

Wen-Li Yu(于文莉), Yun Zhang(张允), Hai Li(李海),†, Guang-Fen Wei(魏广芬),Li-Ping Han(韩丽萍), Feng Tian(田峰), and Jian Zou(邹建),‡

1School of Computer Science and Technology,Shandong Technology and Business University,Yantai 264005,China

2School of Information and Electronic Engineering,Shandong Technology and Business University,Yantai 264005,China

3School of Science,Tianjin University of Technology,Tianjin 300384,China

4School of Physics,Beijing Institute of Technology,Beijing 100081,China

Keywords: quantum battery,quantum coherence,maximal extractable work,charging power

1. Introduction

The rapid development of quantum science and technology has greatly promoted the investigations of core physical quantities in thermodynamics, such as work, heat and fluctuation, shifting from the macroscale to the nanoscale.And many efforts have devoted to the explorations theoretically and experimentally.[1–10]Unlike the classical physics,the quantum effects like quantum coherence/squeeze and entanglement in quantum systems can lead the thermodynamic performance of quantum systems to go beyond their classical counterparts.[11,12]For example,using the quantum coherence and squeeze, the Carnot limit can be broken,[13,14]and the reversal heat flow against the direction of negative gradient of temperature can occur.[15–18]In this context,two attractive questions have emerged. How does a quantum system implement the energy storage effectively for the later use by the other system (or load)? What roles can the quantum effects play in transferring energy and improving the system’s capacity? Quantum battery (QB) as a good platform to address the above issues[19–30]has received much attention until recently.[31]

In 2013,Alicki and Fannes,in their pioneering work,[32]formally proposed the concept of QB, and clearly demonstrated the advantage of entangling operation on work extraction of QB. And, they concluded that it is feasible to implement the maximal work extraction when the battery is driven through intermediate entangled states in the discharging process. After that, various models of QB based on different quantum systems, such as a single harmonic oscillator,[26–28]spin chains,[21,33–38]and single/multi-qubit systems,[39–45]have been studied. One of core goals in exploring QB is to understand how the QB realizes the charging and the discharging and whether it can outperform the classical counterpart. Quantum entanglement and coherence as the special features of quantum system have drawn much attention of their roles in QB.And,many researches have identified their constructive effects on enhancement of the QB’s performance,e.g., improving the QB’s capacity[25,41,46–49]and increasing the charging power and efficiency.[45,50–53]However,most of previous efforts have devoted to the explorations of isolated QB implementing the charging process and discharging processes via unitary operation,which requires fine tuning between the initial state and the unitary process. As is well known, it is usually difficult to isolate one system from its surrounding environment completely in engineering. Therefore, it becomes a significant problem to explore the QB’s performance in an open environment (i.e., open QB). Most recently, Barra in Ref. [54] presented a dissipative charging scheme where the QB performed an open charging process by introducing a thermal auxiliary bath (TAB) composed of a number of thermal two-level atoms (TLAs). The author demonstrated that it is possible to charge the QB, under an external agent driving, from an initial thermal passive state to an active state in an open thermal bath (or environment),verifying that one could extract work from a thermal quantum system with a thermal passive state by the cyclical unitary operation. In addition, there have been many researches focused on different aspects,[41,55–60]e.g.,using the Floquet engineering to overcome the aging of a QB,[41]stabilizing open quantum batteries by structure engineering[57]and sequential measurements scheme,[58]identifying quantum speed-up via a collision charging scheme,[59]highly efficient charging and discharging through shortcuts to adiabaticity,[60]and so on.Though these researches have provided many interesting results in open QB, the rich underlying features and physical mechanism of open QB performing have not been demonstrated enough. Especially, the effects of quantum coherence and entanglement in nonequilibrium bath (or auxiliary bath)on the performance of open QB are worth studying in depth.

Recently, a powerful tool for studying the dynamics of open quantum system,[61–64]namely, collision model (CM)method[65]has been developed. It has been widely used in the quantum information process and quantum thermodynamics, especially in the investigation of the roles of quantum effects of nonequilibrium bath in thermodynamics,[66–70]as well as the strong coupling thermodynamics.[71]So far,the general thermodynamic framework of CMs has been established.[72–74]Based on the framework of CMs, the QB models with collision charging protocol have been constructed.[54,59]Being different from the single-qubit collision charging battery with TAB in Ref.[54],a multi-level collision charging battery with a coherent auxiliary bath (CAB)has been considered.[59]And,in Ref.[59]the authors demonstrated that under the energy preserving interaction between QB and ancilla, the quantum coherence of auxiliary bath can effectively speed up the energy transfer into QB when the CAB has a negative effective temperature(i.e.,the ancilla remaining the inverse populations is required). Naturally one will ask whether the quantum advantage of quantum coherence of CAB can still emerge when the CAB is kept at a positive effective temperature(i.e., ancilla without inverse populations). How does the quantum coherence influence the QB’s capacity? These issues are interesting and have not been addressed enough.

Motivated by the above considerations, we, in this paper, investigate a collision charging scheme of a single qubit battery charging with a CAB having positive effective temperature. Specifically,the CAB in our model is composed of a stream of independent coherent ancillae.We allow the ancillae to interact with the QB one by one,mimicking the dissipative charging process.According to the collision charging protocol we demonstrate that the QB with CAB can perform prominent superiorities in the full charging capacity,charging power and efficiency over their classical counterparts (i.e., the situation of QB charging with TAB)due to the ancillae’s coherence of CAB. The numerical simulations clearly demonstrate that to implement a long-time charging protocol is suitable for the QB with CAB in the weak QB-ancilla coupling regime where the QB can obtain a large capacity and have a highly charging efficiency.In addition,we have also found that the presence of coherence of ancilla can lead the MEW of QB to oscillate with charging time. And,for the strong coupling of QB-ancilla,the first peak value can even go beyond that of QB in saturation which also results in a highly charging power of QB with CAB in a short-charging process. These features suggest that with the help of quantum coherence of CAB,the QB can effectively perform the two different charging protocols: the long-time slow charging with large capacity and high efficiency,and the short-time rapid charging with highly charging power only by adjusting the coupling strength of QB-ancilla to the weak and strong coupling regimes.

The remainder of this paper is arranged as follows. In Section 2,we first introduce the charging scheme of open QB.Then, we derive the quantum master equation of QB and analytically obtain the steady-state solution. In Section 3, we review the key indicators characterizing the charging performance of QB,such as the MEW,charging saturation,average charging power and charging efficiency. And, some analytical results are obtained. In Section 4,we numerically discuss the influences of coherence of auxiliary bath and the coupling strength of QB-ancilla on QB’s performance at length. In Section 5,we briefly summarize our work.

2. Model and charging dynamics

Any charging process involves auxiliary systems that provide the charge (or energy),[54,59]such as a thermal engine,[4,75]an external field,[76–79]or a nonequilibrium system.[28]Here,we characterize the charging process by using a CM protocol(see Fig.1), that is, allowing the identical independent ancillae of auxiliary bath interacting with the battery in subsequence by an external driving (or agent) to be used to mimic the charging process. Here, we assume that each ancilla only interacts with the battery once,and the timeindependent interactionVbetween the ancillae and the battery is the same for each ancilla. When the auxiliary bath is a thermal bath consisting of thermal ancillae,a thermal QB without coherence can be formed, and a coherent QB is for the auxiliary bath composed of coherent ancillae,i.e., the CAB.The QB, after a long-time charging, will reach a saturation level and the whole charging process ends. The resulting Hamiltonian of battery plus ancilla in each charging step reads

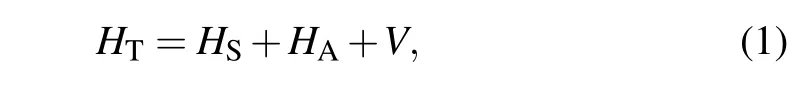
whereHi=wi(+I)/2,i=S, A, (set ħ=1) are independent,i.e., the free Hamiltonian of system (or battery) and Hamiltonian of ancilla (A), withwSandwAbeing the corresponding transition frequencies between the excited state|1〉and the ground state|0〉, I being an 2×2 identity matrix,and the interaction of QB-ancilla implemented by an external agent(or power resource)is given as[54]

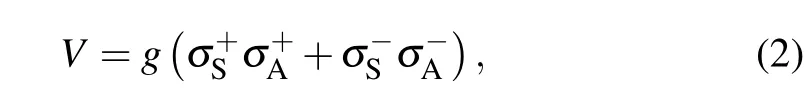
wheregis a coupling constant,=(±)/2 are the raising operator (σ+) and lowering operator (σ-) with Pauli matricesσj,j=x,y,z. To consider the system and auxiliary bath to be initially independent,the total density matrix can be written asρtot(0)=ρS(0)⊗ρA(0)⊗NwhereNrepresents the number of auxiliae in bath,and

whereZA=Tr[exp(-βHA)] is the partition function,θandρthare independently the relative phase and the thermal state corresponding to the diagonal part of pure coherent stateρcoh,α(0≤α ≤1) is a weight parameter determining the ratio between two components:ρthandρcohin the initial state of ancillaρA(0). Meanwhile, it is noted that the parameterαonly appears in the non-diagonal elements ofρA(0). According to the coherence measure ofl1-norm,for an arbitrary stateρthe coherence is given as[80]

whereρmn(m/=n)are the non-diagonal elements ofρ. Thus,the coherence ofρA(0)becomes

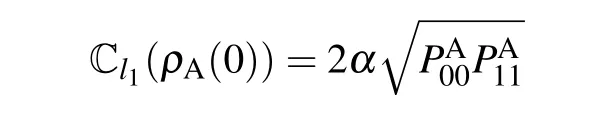
wheren=1,2,...,N,andHAn=HAdenotes the Hamilton of then-th ancilla with initial stateρAn(ρAn=ρA(0)).Owing to all the ancillae being identical and each ancilla only interacting with system once,the state of thenth ancilla,after interacting with system,will be mapped fromρAntoas follows:

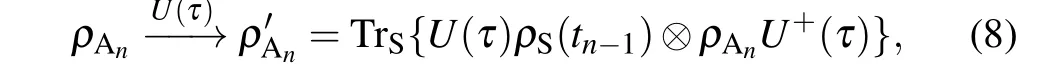
where we,for brevity,have omitted the subscriptnof unitary operatorUn(τ).

Fig.1.Sketch of charging protocol of open quantum battery(QB).The charging process of battery(a single-qubit system)is mimicked by a series of twolevel atoms(TLAs)as auxiliary units(or ancillae labeled by Ai with state ρA)coupling to the battery one by one. We assumes that each ancilla only interacts with the battery once, and the time-independent interaction V between the ancilla and the battery lasts for time τ for each ancilla. denotes the state of the ancilla after interacting with the battery. The thermal(coherent)QB without(with)coherence can be formed when the thermal(coherent)ancillae with ancilla’s state ρA=ρth(thermal state)(ρA=ρcoh(coherent state))are considered.

2.1. Quantum master equation

Now,we focus on the quantum master equation of the system in the charging process. To consider the short-time limitτ →0 the unitary evolution operatorU(τ) in Eq. (7) can be expanded to the second orderO(τ2)as given below.

whereUjkare the matrix elements ofU(τ) in energy basis{|0〉,|1〉}ofHAand written as

withξ=gτand=wτ. Suppose that the system withρS(t)at timetis coupled to a new ancilla,then the state of system,after a time intervalτ,i.e.,at timet+τ,will become

where TrAdenotes the trace over the degree of ancilla with HamiltonianHA. The rate of change of system’s state in each step with a very short interaction timeτis described as

Submitting Eq. (10) into Eq. (11) and using the elements ofU(τ)given in Eq.(9),after some simple algebras,we can obtain the quantum master equation of system with CAB to be

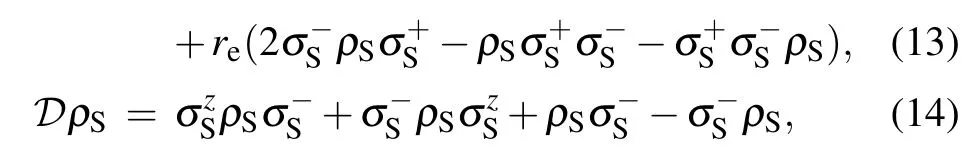
whererd=ξ2/2 andre=ξ2/2. Here, it is noted that the non-diagonal elements of ancilla() appear in both the unitary evolution (the first term on the right-hand side in Eq. (12) and the dissipative part (the third term in Eq. (12))which implies that the coherence of bath will contribute not only to the unitary dynamics of system but also to the dissipation. In addition,it is noted that the master equation(12)is valid in the weak coupling regime,i.e.for the small coupling parameterξ=gτin each charging step. The reason is that the derivation of Eq. (12) has used the approximated unitary operatorU(τ)as given in Eq.(9)holding only for smallξ. In terms of the master equation(12),one can obtain the solution of system steady state in weak coupling regime as discussed in the following subsection,but for finite(not weak)coupling regime,the above master equation will be invalid and the dynamics of system should be carried out via Eq.(10).

2.2. Steady state of QB

which corresponds to a non-coherent battery without coherence (== 0). Meanwhile, the steady state of QB only depends on the population distribution of ancilla, and has a population inversion distribution ofρth,i.e.,=and=,which is consistent with the result reported in Ref.[54].

In addition,based on Eqs.(15)and(16),the steady state of the system in the weak coupling limitδ →0 can be expressed as

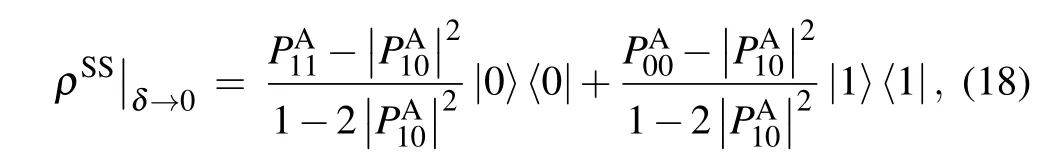
which presents a diagonal distribution similar to that of system evolving in the TAB.But,from Eq.(16)it can be noticed that the excitation population of system in the limit ofδ →0 is related to the coherence of initial state of ancilla. And,it can be verified readily that

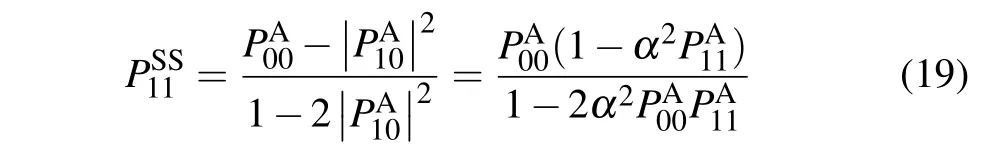
is an increasing function ofα(0≤α ≤1) and≤≤/(1-)with the lower bound and upper bound corresponding toα=0 for thermal ancilla andα=1 for pure coherent state of ancilla, respectively. It also implies that the larger the coherence magnitudeα,the more the storage energy of QB in saturation becomes,that is,the capacity of QB is positively associated with the coherence of ancilla contained.

3. Charging properties of open QB

3.1. External driving energy

In our collision charging scheme of QB,the repeated coupling/interaction of QB-ancilla mimics an open charging process. It is noted that the charging process in our model involves an external agent acting as a power source to supply the“charge”(or energy)to the QB due to[U(τ),H0]/=0 withH0=HS+HAthe free Hamiltonian of compound system of QB plus ancilla. The non-commutator implies that the energy of QB plus auxiliary bath is non-conserving, and an external resource,i.e.,the external agent(or power source)[23,24]exists.In an arbitraryn-th charging(or collision)step the externally driving energy is divided into two parts: one is the increment of energy of QB and ancilla,and the other is the switch-on/off cost at the beginning/end of each charging step.[84,85]Here,the energy captured by QB and then-th ancilla can be independently expressed as

whereρS(tn)andare given in Eqs.(6)and(8). In terms of the usual definition of work for a system to do in a finite-time dynamical processt ∈[0,T]the average work done on system is written as[86]

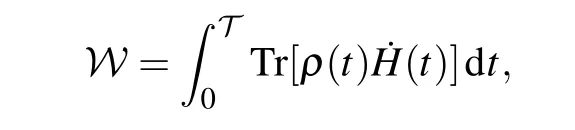
with the time-dependent HamiltonH(t) and the corresponding stateρ(t). The average workWrepresents the energy contribution caused by the energy level shift of system during the evolution timeT. In fact, the above definition of average work done on system is also suitable for characterizing the work done on system in a quench dynamical process, such as the switch-on/off operation withT →0 where the state of system almost remains unchanged due to the infinitely short time evolution,i.e.,ρ(t)≈ρ(0)≈ρ(T), and the differential ˙H(t)=[H(T)-H(0)]/T. In such a situation the common expression of average work will reduce toW=Tr[ρ(T)H(T)-ρ(0)H(0)].Thus,the switch-on/off cost at the beginning/end in then-th charging step can be expressed as

Here,it is noted that when focusing on the thermodynamics of the elementary process of durationτ(i.e.,no switching-on/off dynamical process is considered)as discussed in Ref.[54]the net work done by the agent in Eq. (23) reduces to=ΔQn+ΔUn, which is the same as the one, named “switching work” (no switch-on/off cost is included) in Ref. [54]. However,the switch-on/off costis usually nonzero and it is a physical quantity of interest in this work. Therefore, when the charging time reachestN=Nτthe respective total energy captured by the QB and the auxiliary bath, and the switching on/off cost,respectively,read

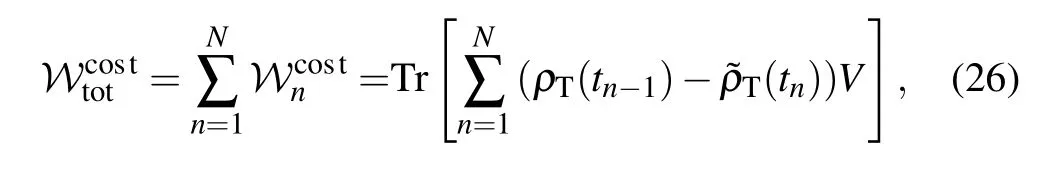
whereρT(0)=ρS(0)⊗ρA(0)is the initial state of composite system of QB plus the first ancilla before charging QB.Thus,the total work performed by external agent,denoted by,equals the sum of energy achieved by QB,auxiliary bath,and the switching on/off cost,and is expressed as

Interestingly, combining with Eqs. (3), (4), (6), (8), and (9),after simple algebra is conducted, one can verify that the total energy independently captured by the QB and the auxiliary bath from the external agent are equal and can be given as

3.2. Indicators of QB’s performance

In a work protocol,MEW can be used to characterize an important quantity,i.e. QB’s capacity. For a system with an arbitrary stateρSthe MEW can be usually described by the difference of free energy of system between the stateρSand the corresponding passive stateσβ,that is,[47,52]

where the free energyF=U-TS, withU=Tr(ρSHS) andS=-Tr(ρSlogρS)being the internal energy and the von Neumann entropy of the system. Thus,one can rewrite Eq.(30)as follows:

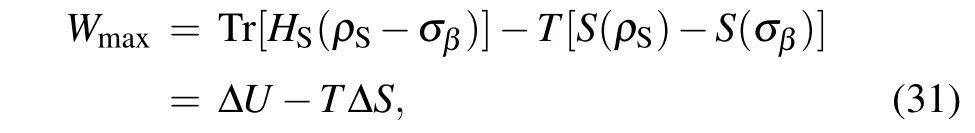
where ΔU=Trand ΔS=S(ρS)-S(σβ)correspond to the decrement of internal energy and the decrement of internal entropy of system from stateρStoσβ,respectively.The charging saturation is another significant quantity to describe how the capacity(or MEW)of QB in the charging process is close to saturation level(i.e.full charging). It is usually defined as the ratio of the MEW of QB at any timetf,Wmax(tf),to the full charging MEW denoted asof QB,[16]i.e.,

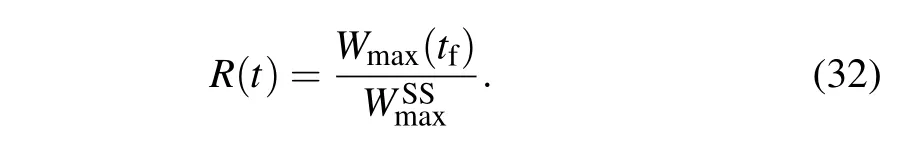
In addition,the average charging power and the efficiency are two key indicators to depict the charging performance of QB.Assume that a QB, after a time lapsetf, is charged from an initial passive (or empty) state denoted asσS(0) to an active stateρS(tf) and the total cost of external agent is, the average charging power of QB can be defined as[22,25,87]

withWmax(tf)=F(ρS(tf))-F(σS(0)). And,the charging efficiency is defined as the ratio of the MEW of QB at timetfto the total driving energy,i.e.,[54]

where the driving energyis given in Eq.(29).

4. Numerical simulation and discussion

In this section, we mainly focus on the performance of QB in the finite coupling of QB-ancillae and different coherence magnitudes. Specifically, we will investigate the effects of the coupling strength of ancilla-QB and coherence magnitude of ancilla on the MEW, charging saturation, average charging power and charging efficiency at length.

4.1. MEW of QB

According to Eqs. (15), (16), and (31), we, in Fig. 2(a),plot the variation of MEW,,of QB with coherence magnitudeα(0≤α ≤1) and the coupling strengthδ(0＜δ ≤5) when QB is charged into the saturation level,i.e.,the steady state of QB (or full charging) is reached. We choose=0.2,=0.8 andw=1.5, which impliesβ=w-1ln()≈0.924, which is the effective inverse temperature of auxiliary bath.

From Fig. 2(a), it can be seen that for CAB with fixed nonzero coherent magnitudeα(0≤α ≤1)the MEW of QB at the saturation level,, always decreases with coupling strengthδincreasing.It implies that increasing the QB-ancilla coupling always suppresses the capacity of QB, but for the TAB withα= 0 the MEW remains unchanged due to the steady state of QB being independent ofδ(see Eq. (17)).Here,it is noted that the feature of QB’s MEWvarying with coupling strengthδis dependent on the QB model. For the isolated battery model,the MEW of QB always behaves as a periodic oscillation with the coupling strength(e.g.the isolated single-qubit and harmonic QB model in Ref.[27]).However,for the open charging QB it is usually not that case. The feature of the QB’s MEW becomes complex. Except for the coupling strength of QB-bath(or environment)it may be influenced by some other physical parameters of open QB model.For example,in the extended Dicke QB model[45]it is demonstrated that the MEW of QB also strongly depends on the external driving field strength,and the effect of internal coupling strength of QB on the QB’s MEW is shown in anN-qubit spin chain QB.[38]Moreover, combining with Figs. 2(a)–2(c) we can see that the feature of QB’s MEW varying with coherent magnitudeαof ancillae strongly depends on the coupling strength of QB-ancilla. Specifically,for the relative small and large coupling strengthδindependently corresponding to the regimes I(0＜δ≾1.28)and III(1.4 ≾δ ≤5)the MEW,,of QB behaves as the monotonically increasing and decreasing functions of coherent magnitudeα,which are also clearly shown in Fig.2(b). While, the MEW first increases and then decreases in the narrow middle regime II (1.28＜δ ＜1.4),which can be seen clearly in Fig. 2(c). Meanwhile, from Fig. 2(c) one also notices that when the coupling reaches the critical valueδ=1.4 the CAB cannot exhibit superiority over TAB on the MEW of QB in saturation. Thus,it demonstrates that the MEW of QB is determined by the coupling strength and the coherence magnitude of ancilla together. And, for the relatively weak/strong coupling of QB-auxiliary bath the MEW of QB in saturation is positively/negatively correlated with ancilla’s coherence,i.e., compared with the situation of TAB(α=0)the coherence of CAB can enhance/suppress the MEW of QB charging with the relative weak/strong coupling of QB-ancilla.

In addition,in order to demonstrate the characteristics of MEW of QB assisted with the CAB/TAB in the charging process, the plot of MEW of QB varying with charging timetn(tn=nτ) at different values of coupling strengthδare given when the CAB with pure coherent ancillae (α=1) and the TAB are considered, respectively. From Figs. 3(a) and 3(b)it can be seen that for the CAB the MEW of QB,Wmax(tn,α=1), always oscillates and finally reaches a steady value(i.e. the saturation state of QB). It also means that the MEW(or“charge”)backflow occurs for the QB charging with CAB.Meanwhile, the larger the coupling strength, the more obvious the oscillation amplitude is and the smaller the MEW of QB in saturation becomes. For simplicity,to denoteas the MEW at the first peak with charging timetPeak, one can notice that for the strong coupling the first peak value can go beyond the full charging value,i.e.,＞as shown in Fig.3(b),which implies that in the strong coupling regime the first peak timetPeakcan be regarded as an optimal charging time. This is very different from the situation of QB charging with TAB (α=0) where the QB MEW’sWmax(tn,α=0)monotonically increases as charging time reaches the same value,(α=0)=0.9, which is independent of the coupling strength as shown in Fig.3(c).

By comparing Figs. 3(a)–3(c) we can find that for the CAB the QB’s MEW always behaves as oscillation in the charging process with the charging timetn=nτ. However,for the TAB the MEW of QB varies monotonically withtn. Thus, we can conjecture that the oscillation of the MEW of QB is mainly caused by the coherence of CAB. The similar phenomenon has also been demonstrated in the model of anN-spin chain QB charged by a coherent cavity driving field in Ref.[38]where the coherent cavity driving field plays a role similar to the CAB in this work. In addition, as expected, for the CAB or the TAB, the stronger the coupling strength of QB-ancilla, the shorter the full charging time of QB is. In addition, we also notice that though the full charging MEW of QB with CAB, in the relative weak coupling regime(i.e.,smallδ)is larger than that of QB with TAB,i.e.,(α/=0)＞(α=0) shown in Fig. 2 (or Figs. 3(a)and 3(c)), the full charging time is slightly longer for CAB than that for TAB. It can be understood that the appearance of “charge” backflow (i.e. the feature of oscillation of QB’s MEW)caused by ancillae’s coherence prolongs the full charging time of QB.

Fig.2. (a)MEWas a function of coherence magnitude α and coupling strength δ,with parametric space of coupling strength divided into three regimes by the pink solid line with δ =1.28 and the blue solid line δ =1.4,that is,I:0 ＜δ ≾1.28,II:1.28 ＜δ ＜1.4 and III:1.4δ ≤5,and with MEW varying with α for δ ={0.1,0.3,0.5,1}(regime I)and δ ={3,5}(regime III)in(b), and δ ={1.28,1.32,1.36,1.40}(regime II)in panel(c). The other parameters are τ =0.005,and w=1.5.

Fig.3. Variations of MEW Wmax with charging step n corresponding to charging time tn = nτ for (a) some fixed weak coupling δ = {0.1,0.2,0.3,0.4,0.5} and (b) some strong coupling δ = {1,2,3,4,5} for CAB (α = 1), and for panel (c) TAB (α = 0) and δ ={0.1,0.3,0.5,1,3,5}. The other parameters are the same as those in Fig.2.

Here, it is noted that the charging properties of the open QB system generally focus on the steady state in the weak coupling regime. And, it usually takes a long time to implement the full charging and results in a smaller charging power.From Fig. 3(b) we can see that for the CAB, the maximal capacity(i.e. the QB’s MEW) of the QB charging in the strong coupling regime,appears at the first peak rather than at the steady state of QB. As is well known, like the pursuit of large capacity and high efficiency of batteries,fast charging(or highpower charging)of QB is also a core indicator to evaluate the high-performance battery. In this sense, it may be interesting to analyze the performance of QB charging to the first peak to identify whether the QB with CAB,in the strong coupling regime,can carry out the fast charging task.

4.2. Charging saturation

Since the MEW of QB in the charging process becomes oscillatory and the value at the first peak, in the strong coupling regime, can be greater than that of QB in saturation,we will compare the charging saturation of QB with that of the CAB and with that of the TAB, respectively. Here, we only consider the charging saturation of QB when the QB’s MEW reaches the first peak value at charging timetPeak. In Fig.4(a)the plot of MEW of QB with TAB(α=0)and CAB(α=1),(α=0)and(α=1)(the upper labels “Peak” and “SS” denote the first peak value and the full charging value,respectively)varying with coupling strengthδis given. And,figure 4(b)shows the corresponding saturation of QB at the charging timetPeakfor the CAB(α=1)and the TAB(α=0),respectively.

From Fig. 4(a) it can be seen that for the two auxiliary baths,i.e., CAB and TAB, the QB’s saturation at timetPeak,RPeak(α)=(α)/(α), behaves as a monotonically increasing function ofδ. For the coupling strengthδ ≈2.1 the QB’s MEW at the first peak,(α=1),approximately equals that of QB in saturation,(α=1). And,the charging saturation of QB with CAB(α=1)is always much larger than that of QB with TAB (α=0) no matter whether it is in the weak strong coupling regime or in the strong coupling regime,i.e.RPeak(α= 1)＞RPeak(α= 0) with 0＜δ ≤5.Meanwhile, for the CAB the saturationRPeak(α=1) can go beyond 100% when the coupling strengthδis large enough,such asRPeak(α=1)≿1 forδ≿2.1 as shown in Fig. 4(b).It indicates that the coherence of ancillae can significantly increase the capability and charging speed of QB to make QB reach or exceed the full charging MEW of QB in a short-time charging process(i.e.,charging to the first peak value of QB’s MEW at timetPeak).

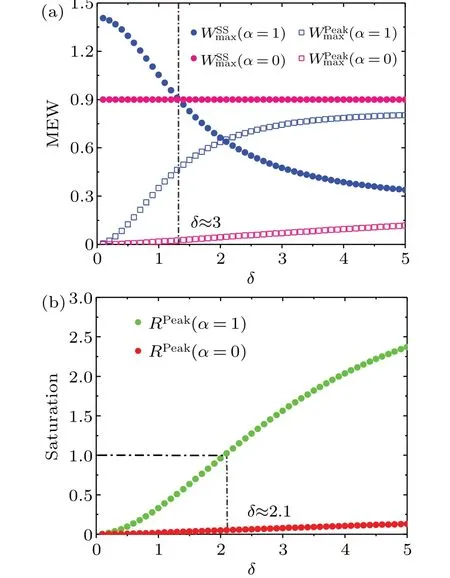
Fig.4.(a)Comparisons of MEWs of QB in full charging and at the first peak time tPeak,(α) and(α), when TAB (α =0) and CAB (α =1)are considered,respectively. (b)Variations of charging saturation of QB at charging time tPeak, RPeak(α) (RPeak(α)=(α)/(α)) with coupling strength δ for TAB and CAB. The other parameters are the same as those in Fig.2.

4.3. Average charging power and efficiency

Average charging power reflecting the charging speed of a battery is a key indicator to characterize the performance of QB. As shown above, the QB’s MEW depends on not only the coherence magnitude of ancilla but also the coupling strength. We, in Fig. 5, plot the variations of average charging power, ¯P(tf,α) defined in Eq. (31), of QB with coupling strengthδfor the CAB(α=1)and the TAB(α=0). And,for simplicity, we consider a case where the QB is charged for a long time (tf=Tcoh,th) to a 99% saturation level (i.e.,R(Tcoh,th) = 99%, here,R(Tcoh) =Wmax(Tcoh)/(α=1)andR(Tth)=Wmax(Tth)/WSSmax(α=0)withTcohandTthbeing the charging times of QB with CAB(α=1)and TAB(α=0),respectively)in Fig.5(a),and also a case for short-time chargingtf=tPeakin Fig.5(b).

Fig.5. Curve of average charging power ¯P(tf,α) versus δ of QB with the CAB(α =1)and the TAB(α =0)for QB charging to approximate saturation with charging time tf=Tcoh for(a)CAB and tf=Tth for TAB satisfying R(Tcoh,th)=99%,and(b)the first peak time tf=tPeak. The other parameters are the same as those in Fig.2.

From Fig. 5(a) it can be seen that the average charging power of QB=P¯(Tcoh,α=1) for CAB and=¯P(Tth,α=0) for TAB, in a long-time charging process, both behave as a monotonically increasing function of coupling strengthδ,which implies that increasing coupling strengthδcan enhance the charging speed of QB. This coincides with our expectation. Meanwhile, we also notice that in the weak QB-ancilla coupling regime, the average charging power of QB for the CAB and the TAB are approximately equal to each other,i.e.,≈in the range of 0＜δ≾0.5. It means that, under the weak QB-ancilla coupling, a longer charging time is required in a full charging process for CAB than that for TAB, while the QB with CAB can still keep a significant average charging power being approximately the same as that for TAB due to the higher capacity of QB in saturation. As the QB-ancilla coupling strength increases to the regime of 0.5＜δ ≤1.0 where(α=1)＞(α=0)still holds,the advantage of average charging power of QB with CAB begins to disappear,i.e.,＞as shown in Fig.5(a),due to the faster decline of the full charging MEW of QB with CAB,(α=1), over the charging timeTcoh. Therefore, in the situation of the weak QB-ancilla coupling and the long-time charging,the advantage of QB with CAB against the QB with TAB lies in the higher capacity of QB rather than the charging power. But,for the short-time charging,tf=tPeak,the average charging power of QB with CAB,=,α=1),is always larger than that of QB with TAB,=,α=0),i.e.＞shown in Fig. 5(b). And, the stronger the QB-ancilla coupling, the more prominent the superiority of charging power for CAB,, over that for TAB,, becomes. This indicates that for the CAB it is more suitable for QB to implement the short-time rapid charging protocol(i.e.,the high power charging scheme).

According to Eq. (32)we, in Fig. 6, make a comparison between efficiencies of QB charging with CAB and TAB in the full charging and the short-time charging (tf=tPeak) processes. Here,we denoteandas the effciiency of QB charging to saturation for the CAB (α=1) and for the TAB(α=0). respectively,andandas the counterparts corresponding to the short-time charging efficiencies. From Fig.6,it can be seen that for the TAB,the efficiency of the QB in the full charging and the short-time charging,i.e.and, are both approximately equal to 25%. That is, for the TAB the coupling strength of QB-ancilla almost has no influence on the charging efficiency. In addition, for the CAB the short-time charging efficiencyof QB,is also insensitive to the coupling strengthδand becomes slightly smaller thanof QB charging with TAB.However,when the QB with CAB performs a full charging(i.e.,a long-time charging),the efficiency,is closely related to the coupling strengthδ.And, it behaves as a decreasing function ofδ, implying that the increasing of the coupling strength can suppress the utilization rate of work supplied by the external agent(or energy source) due to the full charging MEW of QB with CAB also decreasing with coupling strength increasing. But,one should also notice that although the full charging efficiency of QB with CAB,,decreases asδincreases,it is still larger than that of QB with TAB,, in a relatively wide regime,i.e.＞with 0＜δ≾1.9. Therefore,for the CAB the advantage of QB charging, in the weak coupling regime, is the long-time charging with a higher charging efficiency than that for the TAB.Here,it is noted that the intersection withδ ≈1.9 is not universal, which is dependent on the parameters ofαandβ. That is, when we take the parametersαandβdifferent from those (α=1 andβ ≈0.924) selected in Fig. 6 the value of coupling strengthδat the intersection might not be 1.9 anymore.

Therefore, from the above features shown in Figs. 2, 5,and 6, one can conclude that with the help of strong coherence of ancilla of CAB,the QB in the strong coupling regime is suitable for fulfilling the short-time rapid charging protocol with the highly charging power. And, it, in the relative weak coupling regime,becomes feasible for implementing the long-time charging to achieve a larger capacity(or MEW)and higher charging efficiency than the counterparts of TAB.

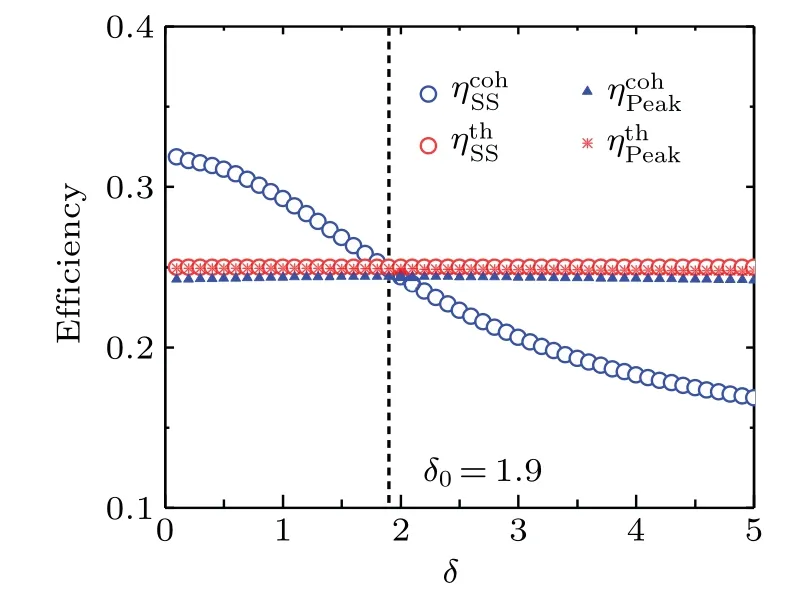
Fig.6. Curves for effciiencies and ( and ) versus coupling strength δ of QB assisted with CAB(α =1)and the TAB(α =0)in full charging(short-time charging tf=tPeak)process. The other parameters are the same as those in Fig.2.

5. Conclusions and perspectives

In this work, we, in the framework of CM, have investigated charging performance of QB assisted with CAB at length,including the MEW,average charging power,charging saturation and efficiency. We mainly focus on the effects of ancillae’s coherence and the coupling strength of QB-ancillae on the QB’s performance,and found some interesting features.We find that the QB’s capacity(or the full charging MEW)in the weak QB-ancillae coupling regime is positively correlated to the coherence magnitude of ancilla of CAB. In addition,it also demonstrates that under the weak QB-ancilla coupling,both the MEW and the efficiency of QB in full charging can go beyond those of QB with TAB. The coherence of ancilla can cause QB’s MEW to oscillate to a steady value in the charging process. Especially, in the strong coupling and strong coherence magnitude regime, the QB’s MEW at the first peak can even exceed that of QB in the full charging, which also results in the higher average charging power of QB with CAB in a short-time charging process than that of QB with TAB.These features suggest that the quantum coherence stemming from the auxiliary bath can not only serve as a useful resource(or“fuel”of QB)to improve the performance of QB but also provide an alternative way to integrate the different charging protocols into a single QB.That is, with the help of quantum coherence of CAB, the QB in the weak coupling regime is suitable to implementing the large capacity and high efficiency long-time charging protocol,and the short-time rapid charging protocol with high charging power can be fulfilled by adjusting the coupling parameter to the strong coupling regime.This work is expected to be beneficial to the in-depth understanding of thermodynamic properties of quantum coherence and the design of high-performance QB.

Acknowledgements

We thank Baoming Xu for helpful discussion.

Project supported by the National Natural Science Foundation of China (Grant Nos. 11775019 and 62173213), the Natural Science Foundation of Shandong Province, China(Grant No. ZR2011FL009), and the Shandong Provincial Science and Technology Support Program of Youth Innovation Team in Colleges (Grant Nos. 2019KJN041 and 2020KJN005).