Improving the teleportation of quantum Fisher information under non-Markovian environment
Yan-Ling Li(李艳玲), Yi-Bo Zeng(曾艺博), Lin Yao(姚林), and Xing Xiao(肖兴)
1School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China
2College of Physics and Electronic Information,Gannan Normal University,Ganzhou 341000,China
Keywords: weak measurement,environment-assisted measurement,teleportation of quantum Fisher information
1. Introduction
Quantum teleportation commendably reveals the difference between classical information and quantum information.[1,2]By sharing the physical resource of quantum entanglement between the sender and the receiver, quantum teleportation can accurately transport an unknown quantum state without transferring the physical carrier of the state.However, in some cases, people pay more attention to a specific parameter encoded in the quantum state than the quantum state itself. The information carried by a physical parameter is usually synthesized by quantum Fisher information(QFI),which is the smallest statistical uncertainty that can be achieved in parameter estimation.[3]As a quantitative measure of information,QFI provides some new insights into quantum information theory, such as inferring Markovian and non-Markovian dynamics[4]and reexamining quantum cloning machines from the perspective of QFI.[5–7]Most recently, it was also recognized that teleporting the QFI of a particular parameter contained in a quantum state would be more economic than teleporting the whole quantum state.[8]
Realistic quantum systems are always inevitably interacting with the environment, which consequently affects the efficiency of QFI transmission.[9–14]This reminds that a key ingredient for an actual and reliable QFI teleportation scheme is that one should be able to deal with the noisy environment. The environmental noises are simply classified into Markovian and non-Markovian types according to the length of environmental correlation time.[15]In the past few years,the studies on non-Markovian dynamics have attracted increasing attentions and achieved remarkable progress in understanding various dynamical features (please see more details in the reviews[15,16]and the references therein). Apart from the fundamental interest of open quantum system dynamics,the applications of non-Markovian memory-effect are widely exploited.[17–19]For example, the authors found that non-Markovian noise has two-fold influences on the fidelity of quantum teleportation: (i)the fidelity exhibits oscillations,and (ii) the fidelity finally decays to zero in the long time limit.[18,19]
Different from the traditional quantum error correction[20]and dynamical decoupling[21]protocols, weak measurement (WM) and environment-assisted measurement(EAM)as new techniques of battling against decoherence,are attracting more and more attention. A WM operation[22,23]is reversible because the measured system does not totally collapse to the eigenstates of the measurement operator.Thus,the initial quantum state could be recovered by a proper measurement reversal operation with a certain probability. Recently,it has been demonstrated that WM can protect the fidelity of a single qubit,[24,25]the quantum entanglement and quantum discord of two qubits and two qutrits from decoherence.[26–31]Moreover, WM has found increasingly wide applications in quantum information tasks.[32–35]Note that some WM-based schemes have been realized in different systems,such as photonic qubits[36,37]and superconducting phase qubits.[38,39]Another promising method for overcoming decoherence is the combination of EAM and quantum measurement reversal(QMR)operations. The underlying mechanism of this method is similar to that of feedback control.The key idea of the EAM scheme is to monitor the noisy environment and then perform the QMR on the system to restore the initial state conditioned on the outcomes.[40,41]In Ref.[41], Wanget al. proposed an EAM-based scheme to recover quantum states decohered by a noisy channel. Compared with the WM-based scheme, the advantages of this new scheme are its higher successful probability and higher fidelity or entanglement of the recovered states.
In this article, we focus on the teleportation of QFI under non-Markovian noisy environments.Unlike previous studies only demonstrating the QFI under decoherence,[42,43]we are concerning about how to use WM and EAM to enhance the teleportation of QFI. We shall show that both of the WM and EAM can counteract the detrimental effects of the non-Markovian noise and improve the teleported QFI, but the strategies are slightly different.In the WM case,the WM operation is performed before the system suffering the noise,while the EAM operation is carried out after the noise. The results show that the EAM scheme is comprehensively superior to the WM one in the improvements of QFI as well as successful probability.
This paper is organized as follows. In Section 2, the teleportation of QFI under non-Markovian noise is discussed.Then, we propose a scheme to improve the teleportation of QFI by WM and QMR in Section 3. In Section 4, the operations of EAM and QMR are performed to improve the teleported QFI.And a comprehensive comparison between these two schemes is shown in this section.Finally,a brief summary is given in Section 5.
2. Teleportation of QFI under non-Markovian environment
We focus on the teleportation of QFI of a phase parameterφcontained in
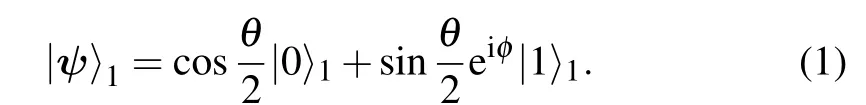
The entanglement channel which is used to teleport the qubit is established as follows. The third party(named Charlie)prepared a maximally entangled state in the form of

Qubits 2 and 3 of the entangled state are distributed to Alice and Bob through the non-Markovian noisy passages, respectively. Here, we consider the qubits resonantly coupled to its own local non-Markovian environment and the environment has Lorentzian spectral distribution
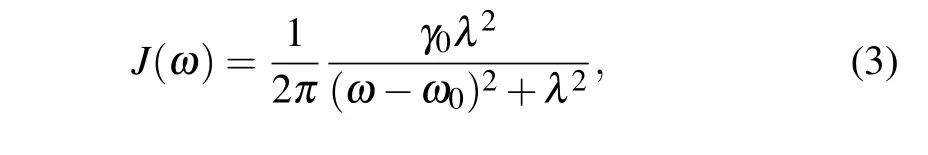
whereω0is the transition frequency of the qubit,ωis the central frequency of the environment,γ0is the decay rate of the excited state under the Markovian limit,andλis the coupling spectral line width related to environment correlation time.Assume the environment is in the vacuum state,then the Kraus operators of a qubit can be written as[44]
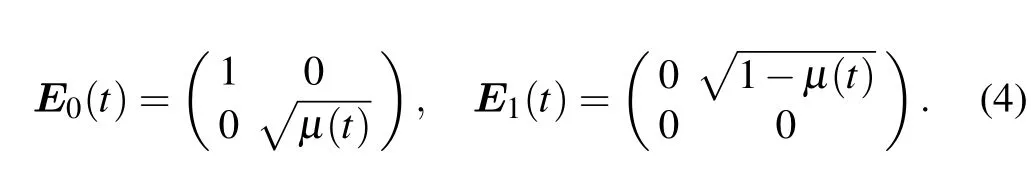
The parameterμ(t)referred in Eq.(4)describes the decay of the qubit caused by the interaction with its non-Markovian environment. It can be given by
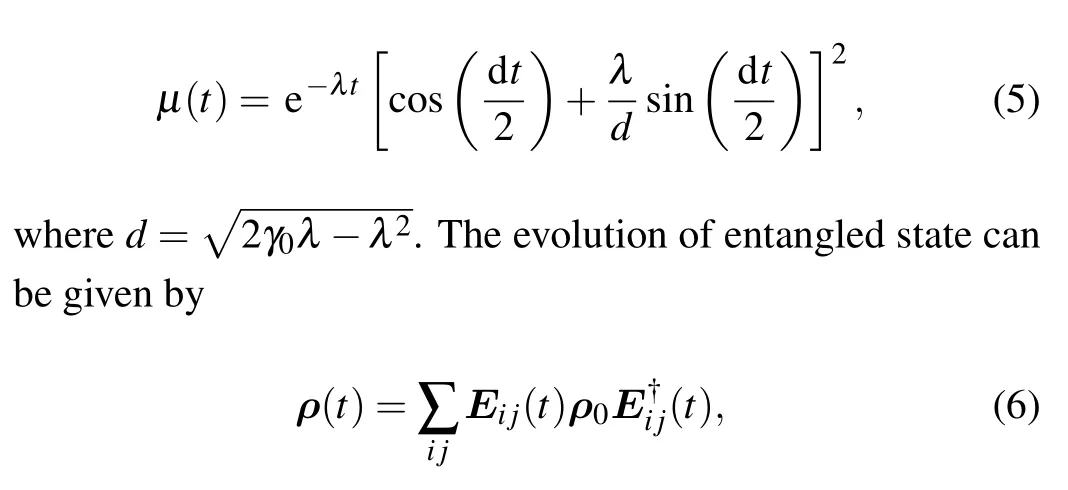
whereρ0=|ψ+〉23〈ψ+|, andEij(t)=Ei(t)⊗Ej(t) (i,j=0,1). Supposing two qubits and their respective environments are identical,after experiencing the non-Markovian noise,the entangled state shared by Alice and Bob becomes

Through the procedure of quantum teleportation shown in Fig.1,Bob finally obtains the output stateρoutgiven by
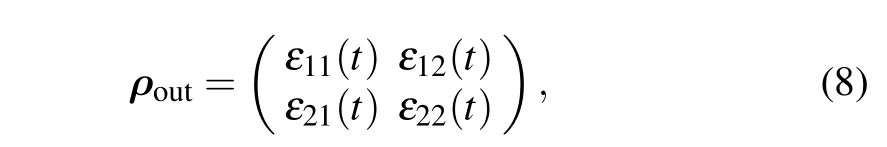
where
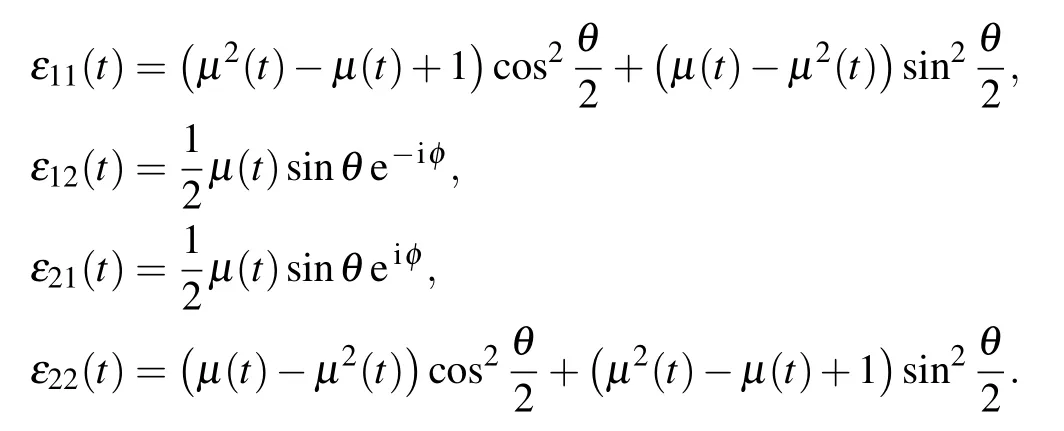
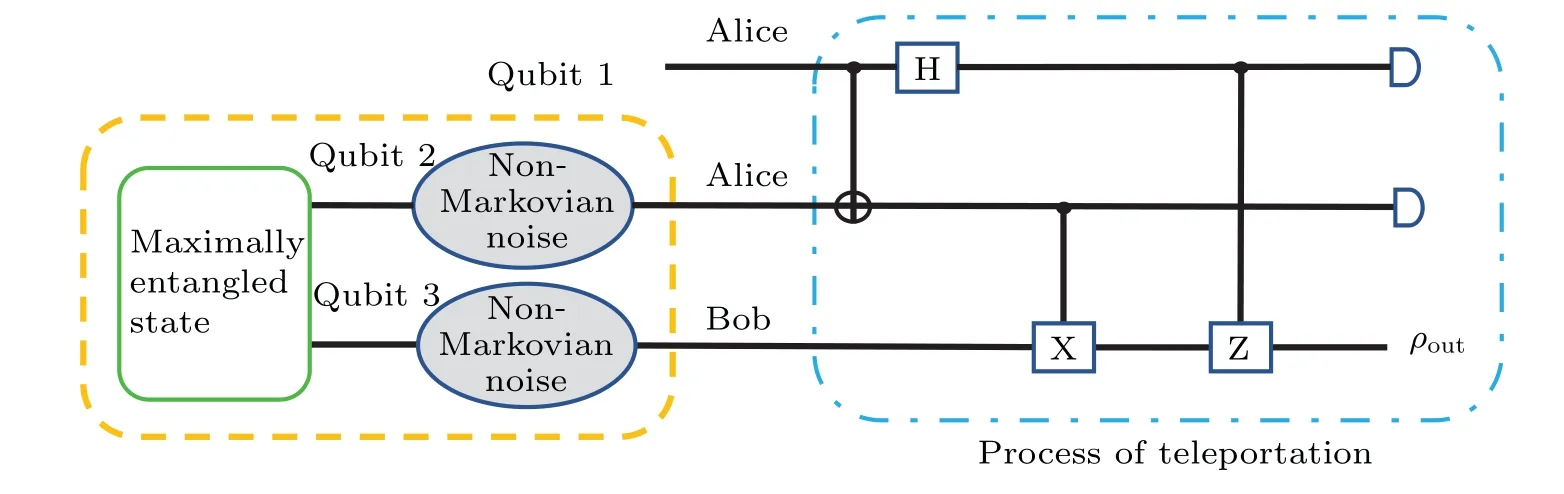
Fig.1. The circuit of quantum teleportation under the non-Markovian noise.
It is well known that any single-qubit state can be written as
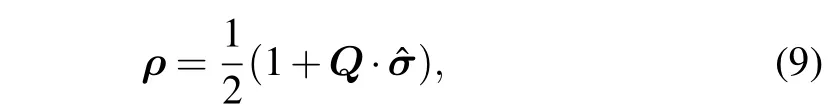
whereQ=(Qx,Qy,Qz)Trepresents the Bloch vector and ˆσ=(ˆσx, ˆσy, ˆσz)represents the Pauli matrices.For single-qubit system, the QFI of parameterφencoded in the state shown in Eq.(9)can be calculated by[45]
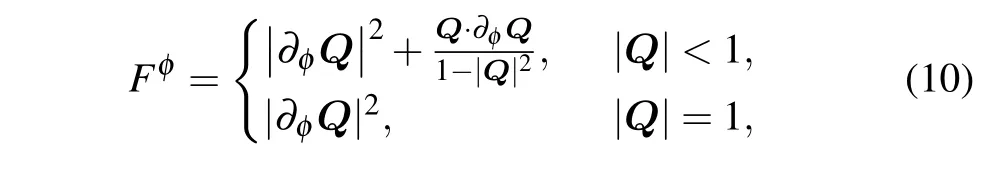
where∂φ(Q) represents the partial differential of the vectorQwith respect to parameterφ. Combining Eqs.(8)–(10),the QFI of the output state can be expressed as

The teleported QFI as a function ofλtis plotted in Fig.2.It can be seen that the teleported QFI decays to 0 after a few damped oscillations. The decay ofFφmeans that the estimation of parameterφbecomes more inaccurate. The damped oscillations characterize the memory effect of the non-Markovian environment, which ensure the information flow back and forth,but it is not enough to keep the teleported QFI in the long time limit. In the following,based on the techniques of WM and EAM,we propose two schemes to enhance the teleportation of QFI.
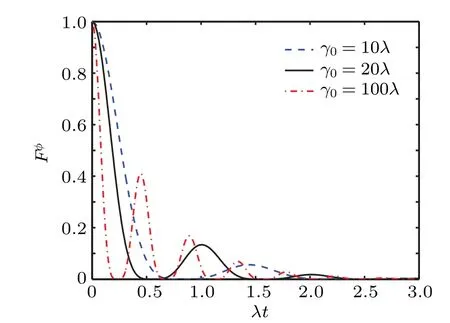
Fig.2. The teleported QFI Fφ as a function of λt under the non-Markovian environment with γ0=10λ,γ0=20λ and γ0=100λ. The other parameter is θ =π/2.
3. Improving the teleportation of QFI by WM and QMR
In this section,we investigate the scheme to improve the teleportation of QFI by WM and QMR. Since the teleportation of QFI is sensitive to the initially shared entanglement,it is crucial to protect the entanglement from the non-Markovian noise. We design three steps to establish the entanglement channel between Alice and Bob,which ensures the nearly perfect teleportation of QFI.
Step 1:Performing WMs on qubits 2 and 3According to Ref. [27], a WM with strengthpjon thejth qubit can be written as the following map:

where 0 ≤pj≤1 (j=2,3). Two pre-WMs are performed immediately on qubits 2 and 3 by Charlie after the maximally entangled state is prepared. Then the state of Eq.(2)becomes

Step 2: Distributing the entanglementCharlie distributes the entangled state to Alice and Bob through the non-Markovian passages. The entangled state shown in Eq. (13)will be evolved into
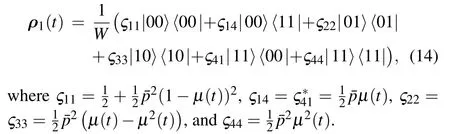
Step 3: Performing QMRs on qubits 2 and 3A QMR operation with strengthqjon the qubitjcan be written as

where 0 ≤qj≤1. After receiving the qubits,two post-QMRs are preformed on qubits 2 and 3 respectively. Then the finally shared entangled state between Alice and Bob is
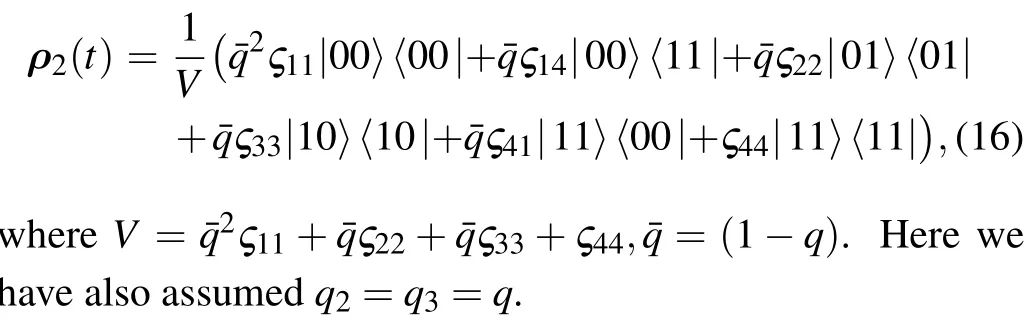
After the process of teleportation shown in Fig.1,the output state can be obtained

where

From Eqs.(9),(10)and(17),the teleported QFI of parameterφcan be calculated as
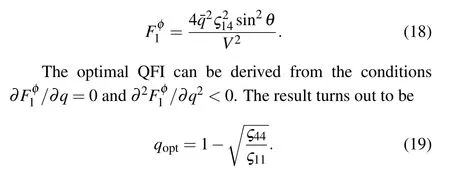
Correspondingly,the optimal QFI can be calculated as
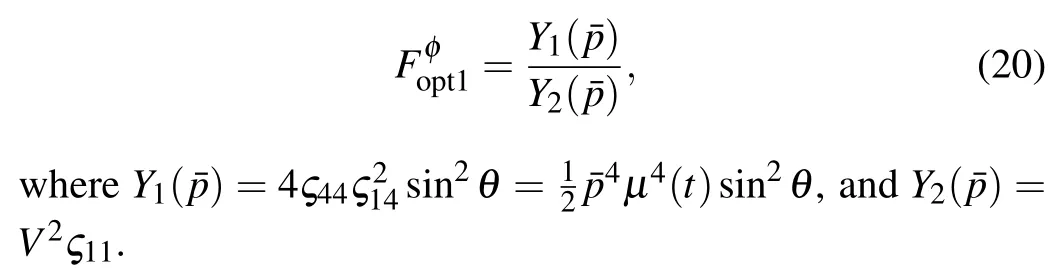
Figure 3 shows the result of the optimal QFIas a function ofλtandp. It is obvious that the teleportation of QFI is significantly improved by the combination of WM and QMR. Even in the severely decoherence cases, i.e.,λt=3,the teleported QFI with the assistance of WM and QMR is always much larger than that without any operation. The physical mechanism could be understood as follows: On one hand,WM can reduce the proportion of|1〉and increase the proportion of|0〉of the qubit,while|0〉is free of the non-Markovian environment. On the other hand, WM is not completely destructive and can be reversed by QMR with a certain probability. Therefore,the pre-WM is taken to reduce the decoherence caused by environment and then the post-QMR is designed to recover the initial state. The combination of them naturally enhances the teleportation of QFI. In addition, the larger the WM strengthp, the more obvious it is to suppress the decay of QFI under the non-Markovian environment,which is shown in Fig.3. It means that the larger the WM strength,the better the improvement of QFI.Whenp →1,the initial QFI can be restored by WM and QMR.

Fig.4. The probability of success P1 versus λt and the WM strength p.The other parameters are γ0=20λ and θ =π/2.
Due to the fact that both WM and QMR are non-unitary operations,the successful probability of this scheme is
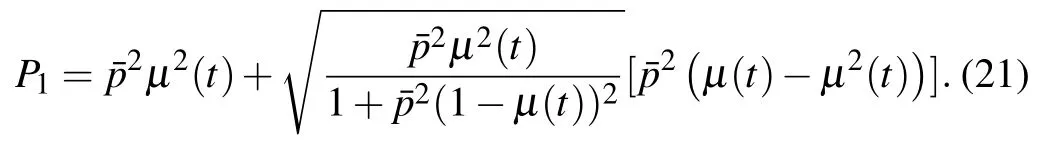
It can be seen that the successful probability decreases with the increasing strength of WM shown in Fig.4. Whenp →1,P1→0. This means that the improvement of teleported QFI is at the price of reducing the probability of success.
4. Improving the teleportation of QFI by EAM and QMR
In this section, we present another scheme to improve the teleported QFI under the non-Markovian environment by EAM and QMR. The underlying idea is that one can choose the reversible process of decoherence though EAM and restore the initial QFI by appropriate QMR.We also consider the entangled state shown in Eq. (2) is prepared by Charlie. Then the entanglement channel used to teleportation is established by three steps.
Step 1: Distributing the entanglementThe distinction from the WM scheme is that the entangled state is distributed without any pre-operation. That is to say, qubits 2 and 3 are sent to Alice and Bob through the non-Markovian passages when the maximally entangled state has been prepared.
Step 2: Performing EAMs on the environmentsThe EAMs are performed during the process of the distribution. It can be implemented as follows. Two ideal detectors are added to monitor the changes of the non-Markovian environments of qubits 2 and 3.If there is excitation change of the environment,the detector will click. We discard the result of clicks(including one and two clicks)and adopt the result of no click. This implies that we only select the decohered processE00which is reversible while ignore the other three decohered processesE01,E10andE11. After that,the state of qubits 2 and 3 evolves into
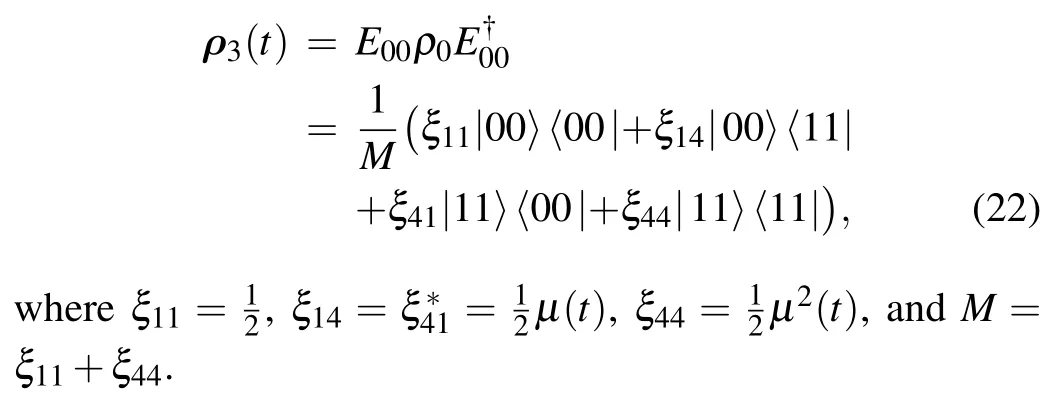
Step 3:Performing QMRs on qubits 2 and 3Alice and Bob perform QMRs on qubits 2 and 3 to restore the initial QFI respectively. Finally, the entangled state shared by Alice and Bob becomes

Through the procedure of teleportation shown in Fig. 1,the output state can be obtained
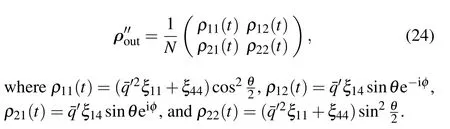
By combining Eqs.(9)and(10),the QFI of parameterφencoded in the quantum state shown in Eq.(24)can be calculated as
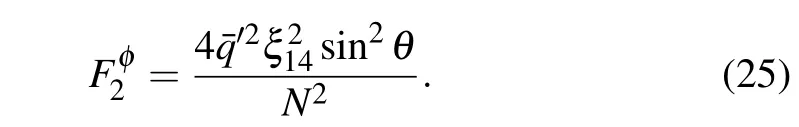
The strengthqcorresponding to the optimal teleported QFI can be also derived from the conditions/∂q′= 0 and/∂q′2<0. The result turns out to be

Substituting Eq.(26)into Eq.(25),we can get

In Fig.5 we plot the evolution of teleported QFI as a function of the timeλt. It can be noted that the teleported QFI can be improved even if the QMR is not performed (i.e.,q′=0).It can be further improved by the combination of EAM and QMR. Particularly, when we take an appropriate strength of QMR,i.e.,q′=,the teleported QFI will be immune from the non-Markovian environment and maintain its initial value.The underlying reason is that the introducing of EAM postselects the quantum system only affected by one decoherence process(E00)which can be reversed by choosing the optimal strength of the QMR.Therefore,the effect of non-Markovian noise is completely removed. Considering that the EAM and QMR are non-unitary operations,the successful probability is given by

It is shown that whether the WM scheme or the EAM scheme,the teleported QFI encoded in the quantum state can be significantly improved. And the initial QFI can be restored by selecting the appropriate measurement strength. From Fig. 5, we observe that the initial QFI can be restored whenq′=. While the initial QFI can be restored by WM and QMR whenq=qoptandp →1 which is shown in Fig. 3.However,the effectiveness of the scheme should also consider the factor of its probability of success. Whenp →1,P1→0.From this point of view, we think the improvement of EAM scheme is better than the WM scheme.
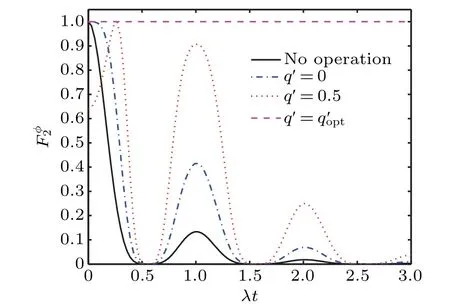
Fig.5. The teleported QFI as a function of the time λt ((solid black line) no operation, (blue dotted lines) q′ =0, (rose red dotted line)q′=). The other parameters are γ0=20λ and θ =π/2.
On the other hand, to ensure an equitable comparison with WM scheme, we introduce the quantity of average improvement of teleported QFI

The behavior ofas a function ofpandλtis shown in Fig.6. An interesting finding is thatis always larger than 0. This means that the efficiency of the EAM scheme is higher than the WM one.This can be understood as follows:the WM,performed before the noise,only collects the information from the system,while the EAM is acted,after the noise,to gather the information from both the system and the environment.Thus,the information collected by the EAM is more than that of the WM.Consequently,the EAM scheme is more efficient to enhance the teleportation of QFI in the non-Markovian environment.
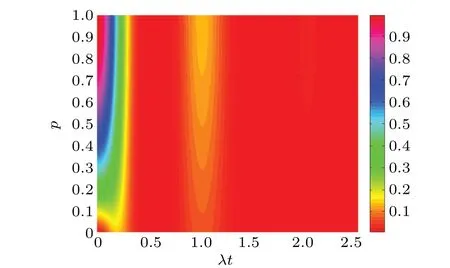
Fig.6. The contour plot of as a function of the p and λt. The other parameters are γ0=20λ and θ =π/2.
5. Conclusion
In summary,we have analyzed the teleportation of quantum Fisher information in the non-Markovian environment. It is found that the teleported QFI decay rapidly with oscillation.Two schemes for improving the teleported QFI encoded by the quantum state are proposed. One is based on WM and QMR.It can be seen that the teleported QFI can be improved. However, the effect is highly dependent on the strength of WM.Only whenp →1, the initial QFI can be restored. Another scheme is based on EAM and QMR.It is found that the initial QFI can be restored and no longer decays over time by selecting the appropriate strength of QMR.Through the detailed comparison,we believe that EAM scheme is more efficient for improving the teleportation of QFI in non-Markovian environment. Although both schemes are probabilistic, they provide a novel way to improve the efficiency of quantum information transmission in open quantum systems.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 61765007 and 12265004),Jiangxi Provincial Natural Science Foundation, China (Grant No.20212ACB211004),and Innovation Foundation of Jiangxi University of Science and Technology (Grant No. XY2021-S088).
- Chinese Physics B的其它文章
- LAMOST medium-resolution spectroscopic survey of binarity and exotic star(LAMOST-MRS-B):Observation strategy and target selection
- Vertex centrality of complex networks based on joint nonnegative matrix factorization and graph embedding
- A novel lattice model integrating the cooperative deviation of density and optimal flux under V2X environment
- Effect of a static pedestrian as an exit obstacle on evacuation
- Chiral lateral optical force near plasmonic ring induced by Laguerre–Gaussian beam
- Adsorption dynamics of double-stranded DNA on a graphene oxide surface with both large unoxidized and oxidized regions

