Transformation relation between coherence and entanglement for two-qubit states
Qing-Yun Zhou(周晴云), Xiao-Gang Fan(范小刚), Fa Zhao(赵发), Dong Wang(王栋), and Liu Ye(叶柳)
School of Physics&Optoelectronics Engineering,Anhui University,Hefei 230601,China
Keywords: entanglement,coherence,first-order coherence,entanglement of formation
1. Introduction
Entanglement and coherence are two important physical resources in quantum information theory.Schr¨odinger put forward the concept of entanglement as early as 1935.[1]Quantum entangled states are the most crucial physical resource in quantum information processing and can be widely used in reality,such as super-dense coding,[2]quantum teleportation,[3]and remote state preparation.[4]However, one of the problems in entanglement theory is how to quantify entanglement. In order to solve this problem, a number of entanglement measures were proposed, such as entanglement of formation,[5]concurrence,[6]negativity[7]and relative entropy of entanglement.[8]There is a monotone increasing relationship between entanglement of formation and concurrence of an arbitrary state of two qubits.[5]Because the expression of entanglement of formation is too complicated, it can be expressed by concurrence and entropy. Entanglement of formation quantifies the minimum physical resources required to produce a quantum state.[9]Another question arises: How can entanglement be represented experimentally? Thus, concurrence for two-qubit pure systems was proposed.[10,11]In 2009,different from the above-mentioned experimental methods,only one copy of the state was required for each measurement to determine the concurrence of locally observable values of arbitrary multipartite pure states.[12]Until 2012,an experimental measurement method of entanglement of formation in arbitrary dimensional pure states had not been proposed.[13]Therefore,we acquire a feasible way in reality.
Coherence is one of the most important concepts to describe the characteristics of photon stream,[14]and its concept can be traced back to classical optics as a property of waves.Its surprising role in a range of physical, chemical, and biological applications has made it used more commonly.[15–18]In 2014, Baumgratzet al. proposed a framework to quantify coherence and determined that the relative entropy of coherence and thel1norm of coherence were the most intuitive and easy measures to calculate coherence.[19]They also put forward the resource-theoretic viewpoint of quantum coherence.This was followed by a number of works that established a rigorous mathematical framework for the resource theory of coherence.[20–24]Svoziliket al. proved that the relevant parameter quantifying the maximum hidden coherence was the degree of violation of the CHSH inequality in 2015.[25]In the same year, many studies found the relationship between quantum coherence and other quantum resources,such as entanglement,[26]mixedness,[27]and deficit.[28]Streltsovet al. proved that any degree of coherence can be transformed into entanglement through incoherent operation,and provided a clear quantitative and operational connection between coherence and entanglement.[29]In 2016, two basic concepts “coherence distillation” (given by the relative entropy of coherence) and “coherence cost” (by the coherence of formation)were proposed.[30]Quantum coherence also plays an important role in quantum computing.[31,32]Cernochet al. experimentally verified the migration of coherence between the complex quantum systems and their subsystems, and verified the conservation of the maximally accessible first-order coherence while it migrated between classical coherence and quantum correlations.[33]
In recent years, many researchers have studied the intrinsic relationship between coherence and entanglement.[34]These relationships differ markedly due to the variety of resources and measurement methods. The aim of this paper is to establish the relation between entanglement of formation and the first-order coherence, i.e., we propose a concrete expression between them.
The rest of this paper is organized as follows. In Section 2, we briefly review entanglement of formation (EOF)and the first-order coherence, and we write the first-order coherence termed in binary entropy. In Section 3, we find the complementary relationship between the two resources, and verify an inequality relation between them for any two-qubit states by using randomly generated states. Then, a specific example is presented to help us understand this relationship.In Section 4,we propose the concept of maximum accessible coherence. In Section 5, we conclude the article with a brief summary.
2. Preliminaries
There are a lot of measures of quantum entanglement,including entanglement of formation(EOF), concurrence, relative entropy of entanglement, negativity, etc. In this section,we will briefly introduce the definitions of concurrence and EOF and the relationship between them. We introduce the measure of coherence: the first-order coherence.
2.1. Entanglement of formation
Consider a two-qubit composite system,its pure state decomposition(not strictly orthogonal decomposition)is


where TrA(|φi〉〈φi|)and TrB(|φi〉〈φi|)are the reduced density matrix of B and A in pure state|φi〉,respectively. The EOF of mixed state is defined as the average value of the entanglement of formation of each pure state in the pure states ensemble,and this average value takes the minimum of all possible mean values. Therefore,the entanglement of formation of mixed state is defined as[35]

Next, we introduce another measure of entanglement:concurrence. For a two-qubit pure state|ψ〉, its spin inversion state is defined as|˜ψ〉=(σy ⊗σy)|ψ*〉, where|ψ*〉is the complex conjugate of|ψ〉andσyis the Pauli matrix. The concurrence of pure state can be defined as
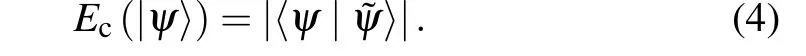
For an arbitrary two-qubit mixed stateρ, the concurrence of mixed state can be expressed as follows:

The minimum value can be obtained by taking over all possible pure state decompositions ofρ, and the concurrence can be written as

whereλn(n ∈{1,2,3,4})is the eigenvalue of non-Hermitian matrixR=ρ˜ρ,andλ1>λ2>λ3>λ4. The spin-flipped density matrix ˜ρcan be expressed as
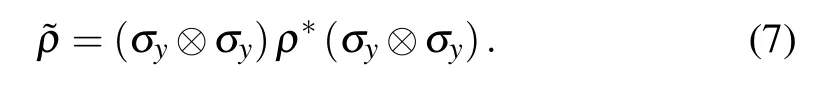
The relationship between EOF and concurrence can be represent by the function[5]

The binary entropyh(x)=-xlog2x-(1-x)log2(1-x).
2.2. The first-order coherence
Let us consider a two-qubit state,ρ=pn|ψn〉〈ψn|,composed of subsystems A and B,wherepnis the descending eigenvalue ofρandpn=1. This quantum state can be obtained by performing operatorVon the separable stateρΛ.Here,ρΛis a diagonal matrix with corresponding eigenvaluespn,and the matrixVcontains the corresponding eigenvectors|ψn〉.Each subsystem ofρhas the corresponding reduced density matrixρA=TrB(ρ)andρB=TrA(ρ). The degree of the first-order coherence of each subsystem is[36]
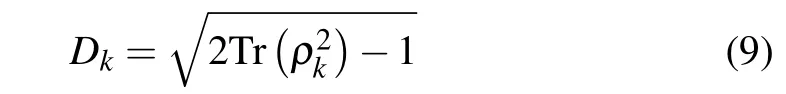
withk ∈{A,B}. When the subsystems are considered independently, the first-order coherence for two subsystems has the following form:[25]

When both subsystems are coherent, one hasD=1, and iff both subsystems show no coherence,D=0.
For convenience, we write the first-order coherence in terms of binary entropy, and use the symbolCto represent it. Its expression of each subsystem can be written as

Moreover,Ckis the monotonically increasing function ofDk.The value range ofCkis the same asDk,Ck ∈[0,1].
Based on Eq.(11),we can rewrite Eq.(10)as

3. The complementary relation between firstorder coherence and entanglement of formation
In this section, we put forward two theorems, which are the complementary relationship between EOF andCfor twoqubit pure state and mixed state. Sequentially, we will prove our theorems.
3.1. Pure states
Theorem 1For arbitrary two-qubit pure state|ψ〉,the entanglement of formationE(|ψ〉)and the first-order coherenceC(|ψ〉)in binary entropy satisfy the following complementary relation
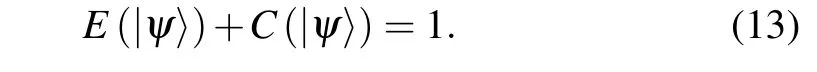
ProofThe relationship between the first-order coherence(D)and concurrence for two-qubit pure states|ψ〉can be written as[37]
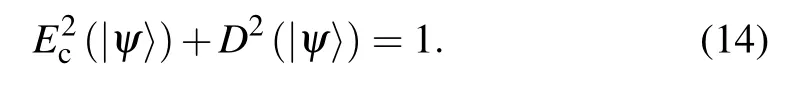
Combining with Eq. (8), we can obtain the relation between EOF and the first-order coherence for two-qubit pure state, it can be expressed as

Due toC=CA=CBfor two-qubit pure state, combining the definition ofC,we obtain
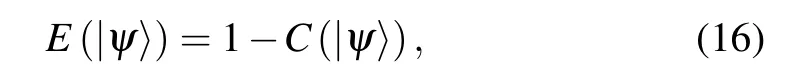
which recovers Eq.(13)as shown in Theorem 1.
3.2. Mixed states
We have proved the relationship between EOF andCin two-qubit pure states before. Naturally, there is a question:What is the relationship between them in two-qubit mixed states? Now we are going to write out the derivation process and to verify the results with random states.
Theorem 2For arbitrary two-qubit mixed stateρ, the EOF and the first-order coherence (C) termed in binary entropy satisfy the following complementary relation as

ProofA quantum system is made up of many different subsystems which can be described by the vector (|ψi〉,i=1,2,...,N). If it is a pure state,its projection operator will beρi=|ψi〉〈ψi|.If the system is mixed ensembles,we can obtain its density operator

Meanwhile,its subsystems can be written as

withk ∈{A,B}. In Bloch space,Eq.(19)is equivalent to the following equation:

whereairepresent the Bloch vector ofρi. Since the modulus of a vector satisfies convexity,we have the following inequality for the modulus ofa:

The first-order coherence of the subsystem is equal to its modulusD(ρk)=|a|.[37]Therefore, the first-order coherence of the subsystem is also convex,

The first-order coherence (C) termed in binary entropy is the monotonically increasing function of the first-order coherence(D),soCalso satisfies convexity
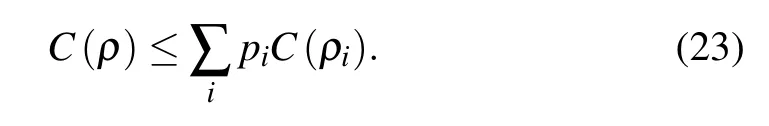
For an arbitrary two-qubit state we can clearly know

According to the definition of entanglement of formation(see Eq.(3)),it is natural to find that EOF satisfies convexity.Thus,we obtain
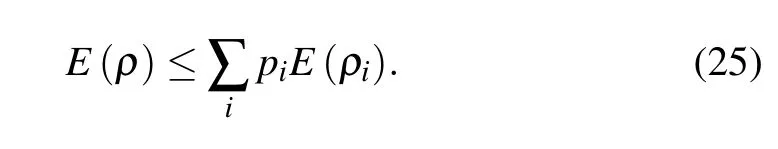
We add the two convexity inequalities for coherence(Eq.(23))and entanglement(Eq.(25)),then we can reach
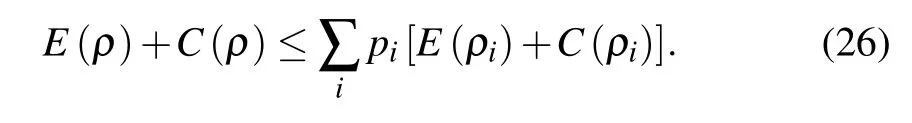
Becauseρiis pure state,the right-hand side of Eq.(26)is going to be 1,which proves Eq.(17)as shown in Theorem 2.
Equation (17) reveals that EOF andCsatisfy the complementary relation. Then we take 20000 randomly generated states to verify our relation, and we plot the EOF andCof these states in Fig.1. We find that all coordinate points are in the region bounded by Eq.(17),C-axis,andE-axis,so Eq.(17)is correct. The upper bound is indeed Eq.(13). According to the above results,we conclude that EOF is anti-correlated withC. The greater theC,the smaller the EOF,and vice versa.

Fig.1. The regional map of entanglement of formation(E)versus the first-order coherence(C)in binary entropy for arbitrary two-qubit states.The upper bounds (purple line) are denoted by E+C=1. The figure plots the entanglement of formation (E) along the y-axis, and the C along the x-axis,for 50000 randomly generated two-qubit states.
3.3. Example
In this section, we will use an example to confirm the above theorems.
The Werner state (ρW) is a combination of the Bell state|ψB〉(maximum entangled pure state) and the maximum mixed state ().Iis the identity matrix with second order. For convenience, we choose the Bell state|ψB〉=(|00〉+|11〉). We take the unitary transformationUfor the Werner state, and we obtain the Werner-typeρthat can be written as
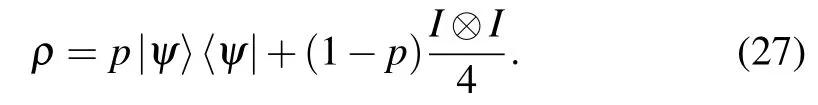
It is obvious that|ψ〉=U|ψB〉. Here,p(0≤p ≤1) is the probability of Werner state becoming Bell state. Ifp >1/3,the Werner state is an entangled state.
In this paper, we find aUoperator that makes Werner state convert to Werner-type state
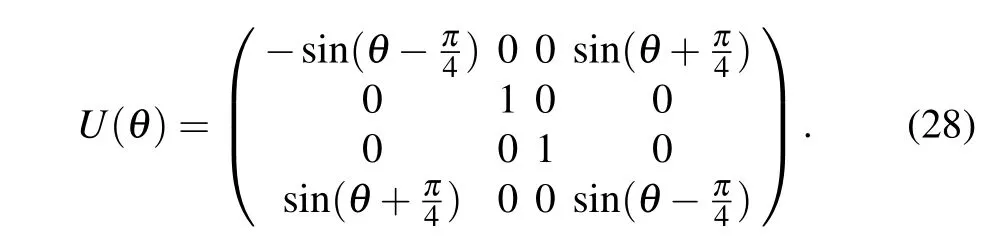

Fig.2. The entanglement of formation E and the first-order coherence C and their sum C+E of Werner-type states with respect to the state’s parameter θ.The blue lines represent p=0.6 and the red lines represent p=0.8.
Since the numerical results are too complicated, we will use the form of pictures to show our results more intuitively.We provide the EOF andCas a function of the parameterθwith differentpin Fig. 2. It can be seen from Fig. 2 that whenθ=π/4,the entanglement of formation reaches its maximum and the first-order coherence(C)is minimum. TheCof Werner-type stateρwill decrease with the increase of its entanglement of formation.
4. Maximum accessible coherence
The maximum accessible coherence is defined as[25]

For two-qubit pure state, we have obtained the equation between EOF and the first-order coherence (C) termed in binary entropy:C+E=1. It is not difficult to find that, when the EOF is minimum (E=0), the first-order coherence (C)reaches the maximum,and the maximum accessible coherence is 1.
We focus on an arbitrary 2×2 dimensional mixed state,which can be expressed as a probabilistic mixture of its eigenvector,as follows:
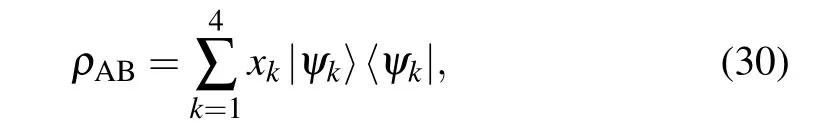
where〈ψm|ψn〉=δmn. Its subsystemρA= TrB(|ψk〉〈ψk|)andρB=TrA(|ψk〉〈ψk|) can be expressed in terms of Bloch vectors as follows:
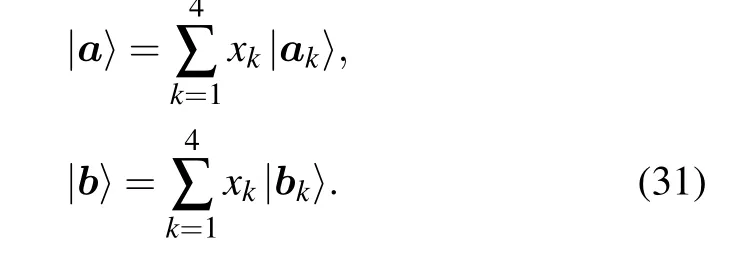
Thus the first-order coherence termed in binary entropy of the stateρABcan be written as
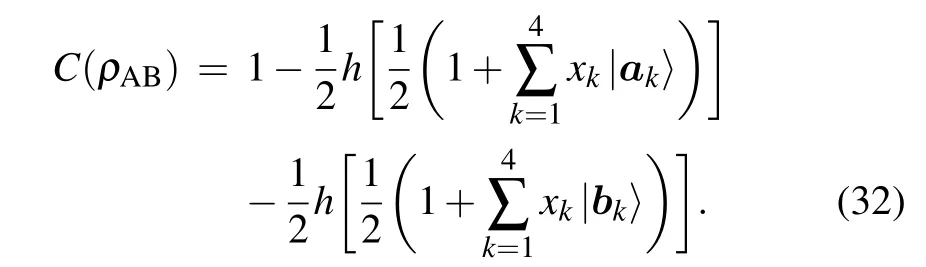
Then, we apply a global unitary operationUto the stateρABand we obtain a post-operation state


The global unitary operatorV†can make two-qubit stateρABobtain the maximum accessible coherence (Cmax). Thus, the maximal accessible coherence can be obtained

5. Conclusion
In summary, we have investigated the intrinsic relationship between EOF and the first-order coherence termed in binary entropy. First,we write the first-order coherence termed in binary entropy. Next, we derive an inequality relation between EOF andCfor any two-qubit states.The relation in pure states is the upper bound of the inequality. We reveal a complementary relationship between EOF andC. The first-order coherence(C)termed in binary entropy is largest when EOF is minimal. Then we give an example to more intuitively reflect the inverse correlation between EOF andC. Finally,based on the above investigation, we propose the maximal accessible coherenceCmax. We indirectly provide the relationship between EOF and the first-order coherence. We hope that our results can provide some help in the mutual transformation of entanglement and coherence.
Acknowledgements
This work was supported by the National Science Foundation of China(Grant Nos.12175001 and 12075001)and the Natural Science Foundation of Education Department of Anhui Province,China(Grant No.KJ2016SD49).
- Chinese Physics B的其它文章
- LAMOST medium-resolution spectroscopic survey of binarity and exotic star(LAMOST-MRS-B):Observation strategy and target selection
- Vertex centrality of complex networks based on joint nonnegative matrix factorization and graph embedding
- A novel lattice model integrating the cooperative deviation of density and optimal flux under V2X environment
- Effect of a static pedestrian as an exit obstacle on evacuation
- Chiral lateral optical force near plasmonic ring induced by Laguerre–Gaussian beam
- Adsorption dynamics of double-stranded DNA on a graphene oxide surface with both large unoxidized and oxidized regions

