紧扣核心条件 强化逻辑推理——一道立体几何题的分析

许志盛

(江苏省江阴市第一中学 214400)

立体几何的考查与应用是历年高考数学试卷中比较常见的基本知识点之一，解决问题的关键是紧扣题目条件中立体几何的核心信息，通过对应的立体几何基础知识，利用立体几何中的空间点、直线、平面等之间相关的位置关系，以及边、角等相关信息，合理强化逻辑推理，正确数学运算，实现立体几何问题的合理推理与应用．

1 问题呈现

问题(多选题)三棱锥V-ABC中，△ABC是等边三角形，顶点V在底面ABC的投影是底面的中心，侧面VAB⊥侧面VAC，则( ).

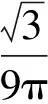
2 试题分析

本题是一道立体几何的多选题，根据题意条件以及创新情境，考生可以直接猜想该立体几何题为一特殊模型——“墙角”，即VA,VB,VC两两垂直，后面4个选项的相应运算和推理判断便不太困难了．另一方面，如果我们需要准确判断这是一个“墙角”问题，或者把这个问题改编为一道解答题， 我们该如何证明?

由题目的条件，三棱锥V-ABC中，△ABC是等边三角形，顶点V在底面ABC的投影是底面的中心，可以比较容易证得这是一个正三棱锥，最后侧面VAB⊥侧面VAC便成为了关键的一个条件，即使我们事先还没意识到这是一个“墙角”问题，但如何运用面面垂直的条件，去进一步挖掘几何体的关系，正是命题人希望考查考生的关键环节!另外还要用到正三棱锥的重要性质：底面正三角形的各边分别与相对的侧棱垂直．

3 问题破解

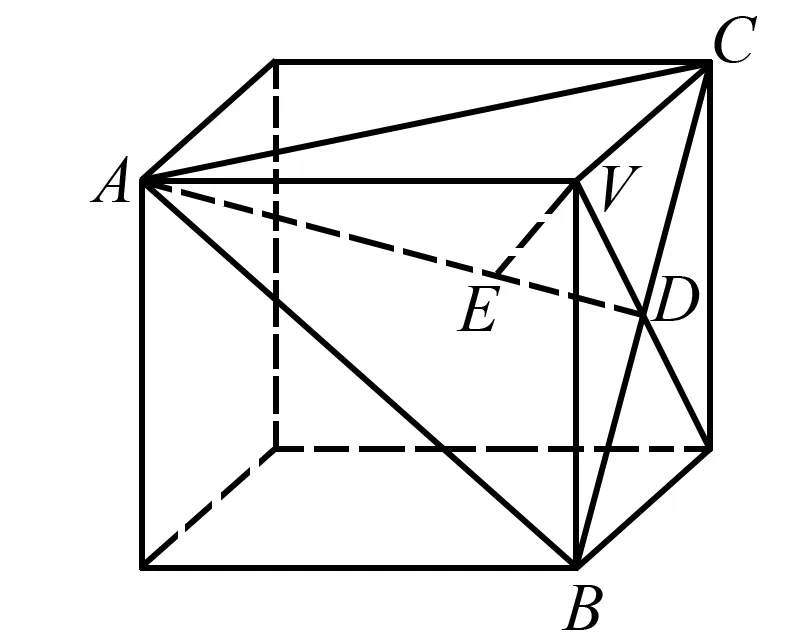
图1

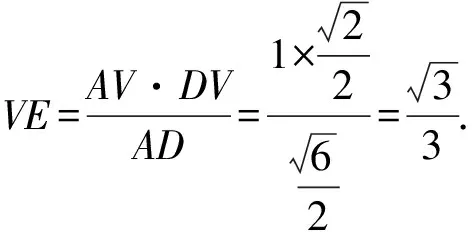
4 追根溯源

以上问题作为多项选择题，如果考生能借助立体几何中的特殊模型——立体几何中的“墙角”意识，可直接利用“墙角”的基本性质与直观图形加以计算并判断选项．如果考生没有上述意识，我们从破解核心条件的角度来看，回归教材，追根溯源，同时也是对上述“墙角”的证明．

题1 (人教版普通高中教科书《数学》(必修第二册)第164页第17题)求证：三个两两垂直的平面的交线也两两垂直．(“墙角”模型)

题2(人教版普通高中教科书《数学》(必修第二册)第160页例10)已知PA⊥平面ABC，平面PAB⊥平面PBC，求证：BC⊥平面PAB．

5 链接高考

在历年的高考数学试卷的真题中，也经常有立体几何中的“墙角”模型及其综合应用，或出现在选择题、填空题这类小题中，或出现在解答题这类大题中，以问题背景的形式或合理转化来体现．

高考真题(2019年高考数学全国Ⅰ卷理科·12)已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为( ).

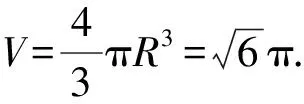
6 变式拓展

结合创新情境的立体几何背景与数学文化的综合应用，从不同思维视角、不同问题背景来巧妙创设，拓展思维，并结合多选题的特征，从多个层面加以发散思维，得到相应的变式拓展问题．

变式1(2021届湖南模拟)(多选题)截角四面体是一种半正八面体，可由四面体经过适当的截角，即截去四面体的四个顶点所产生的多面体．如图2所示，将棱长为3a的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为a的截角四面体，则下列说法正确的是( ).

图2 图3

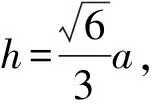
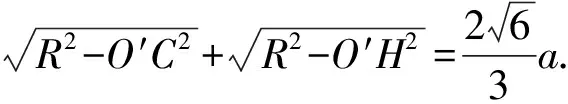
二面角A-BC-D的余弦值应该为负值，故选项D错误．

故选ABC．

变式2(多选题)将边长为2的正方形ABCD沿对角线BD折成直二面角A-BD-C，点P为线段AD上的一动点，下列结论正确的是( ).

A．异面直线AC与BD所成的角为60°

B．△ACD是等边三角形

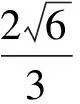
D．四面体ABCD的外接球的表面积为8π

解析对于选项A，因为BD⊥OA，BD⊥OC，OA∩OC=O，所以BD⊥平面AOC，AC⊂平面AOC.

所以BD⊥AC，异面直线AC与BD所成的角为90°，不是60°，所以选项A错；

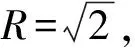
在平时的训练中，我们要及时发现学生在答题中存在问题的“症结”原因，对症下药，合理选题，展开针对性的训练．熟悉掌握一些基本的立体几何特殊模型，如“墙角”模型，组合体模型，在解决选择题或填空题时可以根据题目条件与立体几何模型的关系加以直接应用，在应对解答题时也可以利用条件合理引导，指导推理论证的目标．