例谈二元齐次方程条件下最值求解策略

张志刚

(山东省宁阳县复圣中学 271400)

二元齐次方程条件下的二元函数最值问题作为热门题型，频频出现在高考、竞赛、高校强基计划测试等考试中.该类问题综合性强、方法灵活、变化多端，要求考生具备较高的逻辑推理、数学运算、数学抽象等核心素养.本文按照二元齐次方程条件的结构特征，将此类试题梳理细化为各种具体题型，再研究各种题型相应的最优或通用的解法，以帮助学生快速甄别题型，按图索骥，选择合适的解题策略.

1 已知直线型条件ax+by=c，求f(x,y)的最值

例2(2020年新高考全国Ⅰ卷第11题)已知a>0，b>0，且a+b=1，则( ).

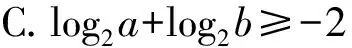
分析通过观察可以发现，尽管四个选项中表达式的结构类型(如二次多项式、指数式、对数式、根式)不尽相同，但本质上都是在共同的二元一次方程约束条件a+b=1下，探求二元函数的最值问题，于是可以考虑上述构造等差数列的方法.

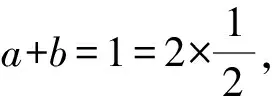
2 已知(ax+by)(cx+dy)=e，求f(x,y)的最值

例3 (浙江省2020年3月“超级全能生”联考(B)第10题)已知实数x,y,满足x2-4xy-5y2=5，则x2+2y2的最小值为____.

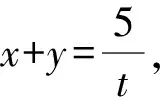
解析由x2-4xy-5y2=5，得

(x-5y)(x+y)=5.

联立上述两式，解得

代入x2+2y2，得

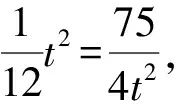
例4 (2017年清华大学中学生标准学术能力测试第12题)已知实数x，y满足5x2-y2-4xy=5，则2x2+y2的最小值是____.

解析由5x2-y2-4xy=5，得

(x-y)(5x+y)=5.

联立上述两式，

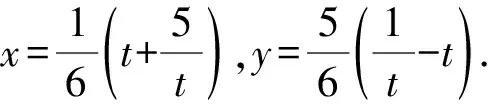
代入2x2+y2，得

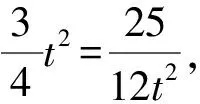
3 已知圆型条件(x-a)2+(y-b)2=r2，求f(x,y)的最值

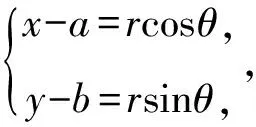
例5 (2020届高考浙江省宁波市高三上学期期末)已知45x2-12xy+52y2=20，求3x2+4y2的范围.

解析因为45x2-12xy+52y2=20，

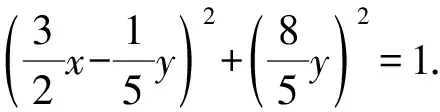
代入3x2+4y2，得

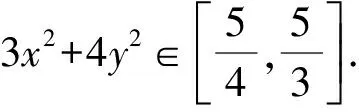
事实上，上述三角代换法也适用于“圆面型”条件下的二元最值问题.

例6 (2020年清华大学强基计划测试第1题)已知x2+y2≤1，则x2+xy-y2的取值范围为____.

4 已知椭圆型条件求f(x,y)的最值

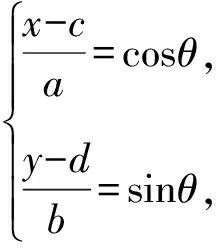
代入目标函数式f(x,y)，将二元最值问题转化为关于θ的一元函数最值问题.

例7(2009年华南理工大学自主招生测试第3题)已知a,b∈R，a2+2b2=6，则a+b的最小值为____.

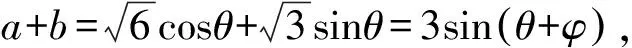
所以a+b的最小值为-3.

可设x=4+2cosθ，y=3sinθ(0≤θ<π)，

5 已知双曲线型条件求f(x,y)的最值.

例10 (2008年南京大学自主招生测试第5题)已知实数a,b满足2b2-a2=4，则|a-2b|的最小值是____.

下同例9.

通过以上各例可以看出，二元齐次方程条件下的二元函数最值问题意蕴丰富，包含函数、方程、不等式、三角代换、解析几何等高中数学主干知识，综合应用函数与方程、转化与化归、数形结合、分类讨论、配方法、换元法、构造法、放缩法、判别式法等数学思想方法，通过多种手段实现消元、降幂、化繁为简之目的.减元思想是贯穿其中的一条主线.教学过程中，要认真剖析题设条件和结论的结构特征和属性，及时提取数学模型，从代数消元、三角代换、不等式放缩、几何意义等视角寻求解题突破口，提升学生的逻辑推理、数学抽象、数学运算、直观想象等核心素养.