例析高考导数压轴题中变更主元的几种视角

魏东升

(福建省厦门双十中学漳州校区 363107)

函数与导数是培养学生逻辑推理、直观想象和数学运算等核心素养的主要载体之一，其一直是高考数学考查的重点内容.在处理函数与导数的压轴题时，对零点的处理往往是一个关键环节，有些超越函数(指不满足任何以多项式作系数的多项式形式的函数，如三角函数、对数函数、反三角函数和指数函数等)的零点确实存在，但无法精确求解，此谓之“隐零点”；有些导数的零点虽然可求，但因含参而需要讨论.对于这类问题，常见的处理方式主要有虚设零点、化隐为显和变更主元三大类.

本文主要探讨这类压轴题中变更主元的几种处理视角.所谓变更主元，是指有些数学问题中常含变量，在某些情况下若按常规思路确定主元可能会导致问题复杂化，若能针对题目的结构特征人为地突出某个变量的主体地位，将之当作主元构造新的函数，则可达到化繁为简、化难为易的目的.这种问题解决的思想方法也称为主元法.

下面结合近几年的部分高考导数压轴题来感受这种策略，以供大家参考.

1 变更主元，构超越函数

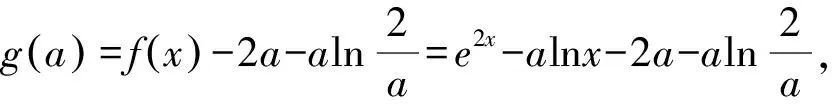
则g′(a)=lna-ln(2ex).

当a<2ex时，g′(a)<0；

当a>2ex时，g′(a)>0，

所以a=2ex时，g(a)取最小值为

g(2ex)=e2x-2ex.

令h(t)=e2t-2et，则h′(t)=2e2t-2e.

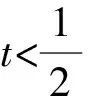
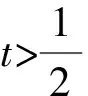
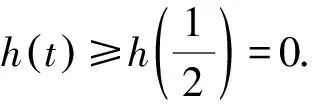
即g(a)≥0.

评注本题常规的一种做法是通过对f(x)进行求导，结合第一问的相关结论发现导函数有隐零点，再虚设零点后进行消“超”代换(指的是把超越函数转化为普通函数)，得到关于隐零点为自变量的一个双勾函数，最终利用均值不等式或求导证得.这种方法对学生的能力要求较高，这里采用了重新构造关于变量a的对数超越函数，此法很好地避免了隐零点的出现.

2 变更主元，构幂函数

例2 (2016年全国Ⅲ卷文)设函数f(x)=lnx-x+1．设c>1，证明:当x∈(0,1)时，1+(c-1)x>cx.

证明当x∈(0,1)时，设h(c)=cx-cx+x-1，c>1,

则h′(c)=xcx-1-x=x(cx-1-1)>0.

所以h(c)在[1,+∞)上单调递增.

所以h(c)>h(1)=0.

所以当c>1，x∈(0,1)时，1+(c-1)x>cx.

评注本题常规的一种做法是通过构造函数g(x)=cx-cx+x-1再进行求导，得到导函数的零点后，再结合前两问的相关结论对零点的范围进行放缩，最终利用g(x)的单调性证得.这种方法其实是命题者在“高考要体现选拔功能”的思想引领之下给出的一种证法，这里采用重新构造关于变量c的幂函数，会发现根本不需用到前两问的结论就使得问题得到完美解决！

3 变更主元,构双勾函数

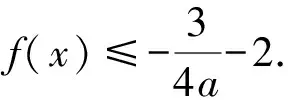
证明原不等式等价于证明

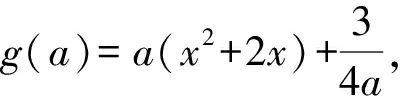
因为a<0，

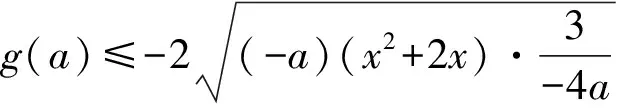
所以原不等式等价于证明

设h(t)=lnt-t+1，

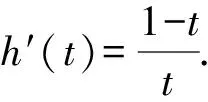
当t<1时，h′(t)>0；

当t>1时，h′(t)<0，

所以h(t)≤h(1)=0．

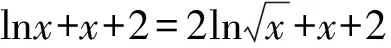
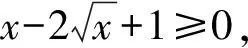
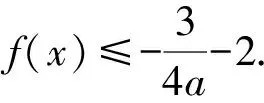
评注这里的证明思路主要是重新构造关于变量a的双勾函数，再利用均值不等式实现消参的目的．较之本题的常规做法(即通过直接求导得到f(x)的最值)并没有优势，这是因为f′(x)的零点并非是隐零点，它可以直接求出来.这也提醒我们在解题时不要盲目地进行主元的变更，有时变更可以事半功倍，有时却可能导致事倍功半，所以应该具体问题具体分析．

4 变更主元,构二次函数

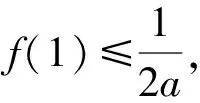
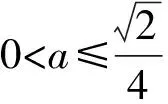
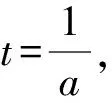
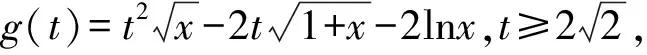
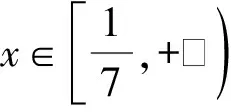
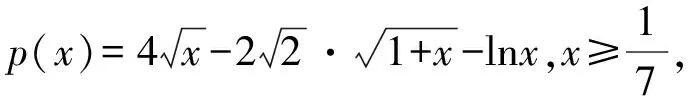
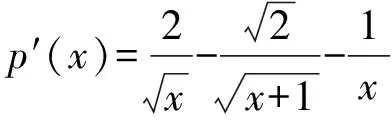
所以p(x)≥p(1)=0．

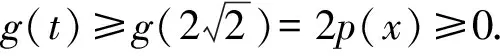
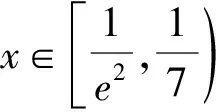
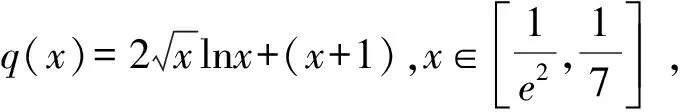
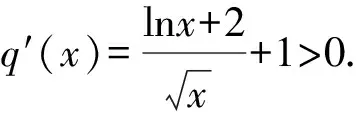
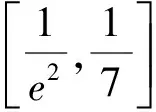
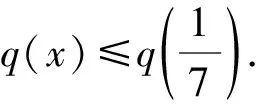
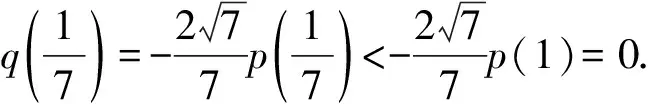
所以q(x)<0．

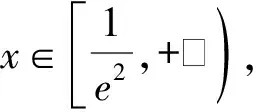
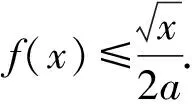
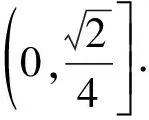
通过上述几道真题我们知道，通过变更主元后构造关于新元的超越函数、幂函数、双勾函数和二次函数等函数进行求解，是处理导数隐零点等问题的常见策略之一．在导数压轴题的教学过程中，像这样以专题的形式介绍隐零点问题的处理策略，尽量一次性彻底地解决与其有关的问题，对学生解题水平的提升、逻辑思维的训练和核心素养的培养，想必都是极好的．