巧用不同方法破解双曲线渐近线相关问题

俞 纲

(云南省昆明市第三中学 650000)

渐进线是双曲线的重要性质，在历年高考的选择题、填空题中多次出现，而且基础题和难题都有涉及，如何针对性地选择适当方法来巧妙解决相关问题，尽量避免复杂的代数计算值得我们研究.

1 用二次方程解决双曲线渐近线的代数计算

1.1 双曲线方程与渐近线方程的相互转化

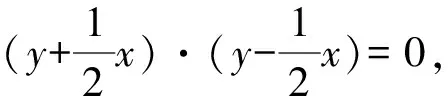
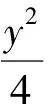
小结上述三题都属于基础中等题，通过方程的代数特征直接设双曲线渐近线的方程进行研究，避免了对两种位置的双曲线分别研究的麻烦.当然，不是所有条件都适合代数方法直接设方程，归纳言之，以下三个代数结论可直接运用：双曲线Ax2-By2=1(A·B>0)的渐近线方程可直接由Ax2-By2=0因式分解得到；以y=kx为一条渐近线的双曲线方程必定可以写为(y+kx)·(y-kx)=λ(λ≠0)，即y2-k2x2=λ(λ≠0)的形式；与双曲线Ax2-By2=1(A·B>0)有相同渐近线的双曲线方程必定可以写为Ax2-By2=λ的形式.

1.2 直线与双曲线的两渐近线相交的问题

一条直线与双曲线两渐近线交于两点的问题，一般需要把该直线分别与两条渐进线方程联立，通过解两个二元一次方程组，得到两个交点坐标后再进行相应的表示与计算，如果把两条渐进线看作一个整体，借助二次方程来表示它，则可以借助直线与二次曲线位置关系的研究方法，运用“设而不求”的思想进行整体计算，避免直接表示交点坐标，达到事半功倍的效果.

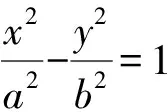
分析此题可以把直线方程写出，再与两渐近线分别联立得到A,B两点的坐标，运用中点坐标公式得到等量关系，但计算相对繁琐，运用二次方程理论则能简化运算.

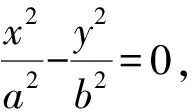
即x1+x2-2m=(y1+y2)(-kAB).

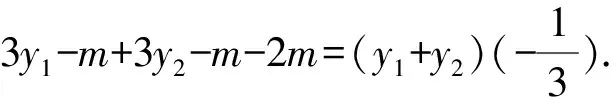
即10(y1+y2)=12m.

(9b2-a2)y2-6b2my+b2m2=0.

代入10(y1+y2)=12m，得a2=4b2.

小结由于双曲线及渐近线都含有未知字母,直线与两条渐近线联立两次分别表示出两交点坐标再计算相对繁琐，若能借助韦达定理巧用“设而不求”的思想进行整体转化,则能简化运算.

2 用几何性质解决双曲线渐近线的几何问题

图1

借助这两个直角三角形，可以更直观地理解渐近线斜率的几何意义，并且可以得到一些常用结论，如：焦点到渐近线的距离为b；以O为圆心，实轴长2a为直径的圆与渐近线相交，交点与焦点的连线恰好与渐近线垂直；以O为圆心，焦距长2c为直径的圆与渐近线相交，交点与顶点的连线恰好与实轴垂直；两渐近线的夹角被坐标轴平分等性质，运用这些几何性质，可以灵活解决一些相关的问题.

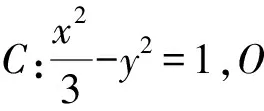
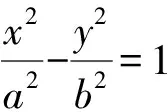
图2

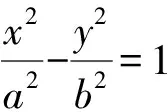
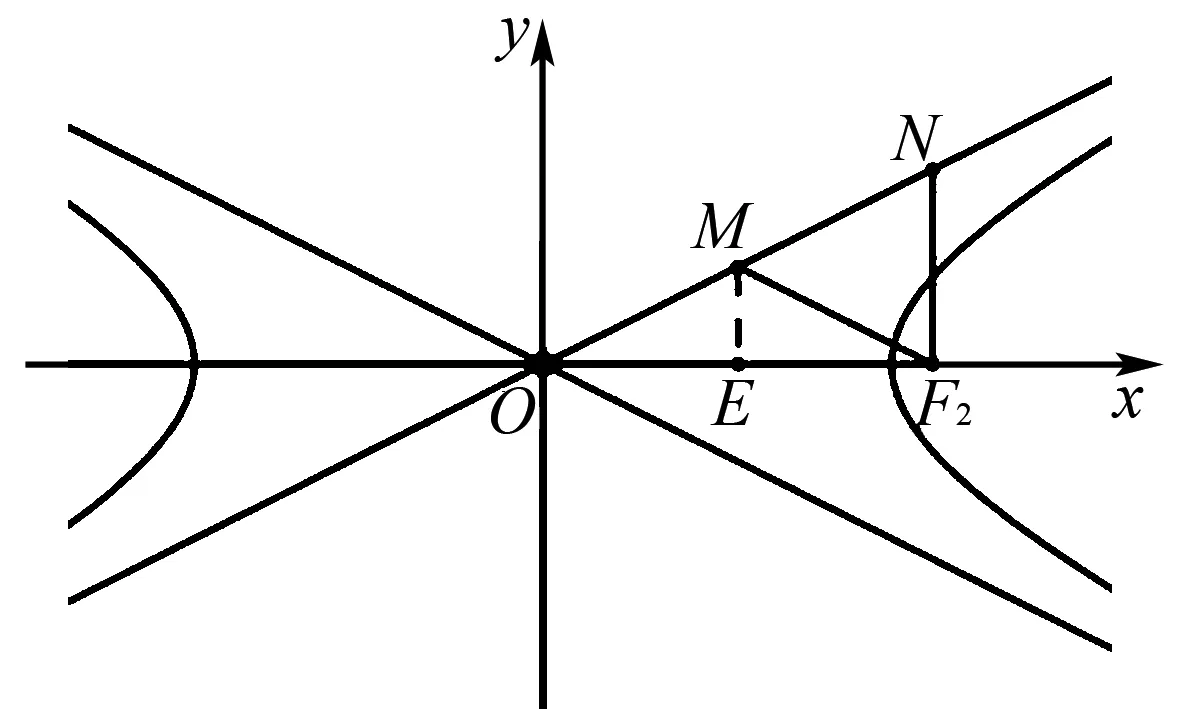
图3

3 根据题目特点选择合适的方法进行求解

分析此题为例10变式，我们分别用三种方法求解，对比运算复杂程度的差异.

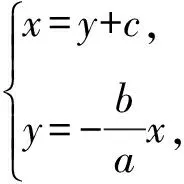
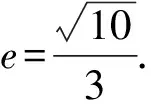
(b2-a2)y2-2bc2y+b2c2=0.

从而得到a2=9b2.

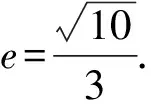
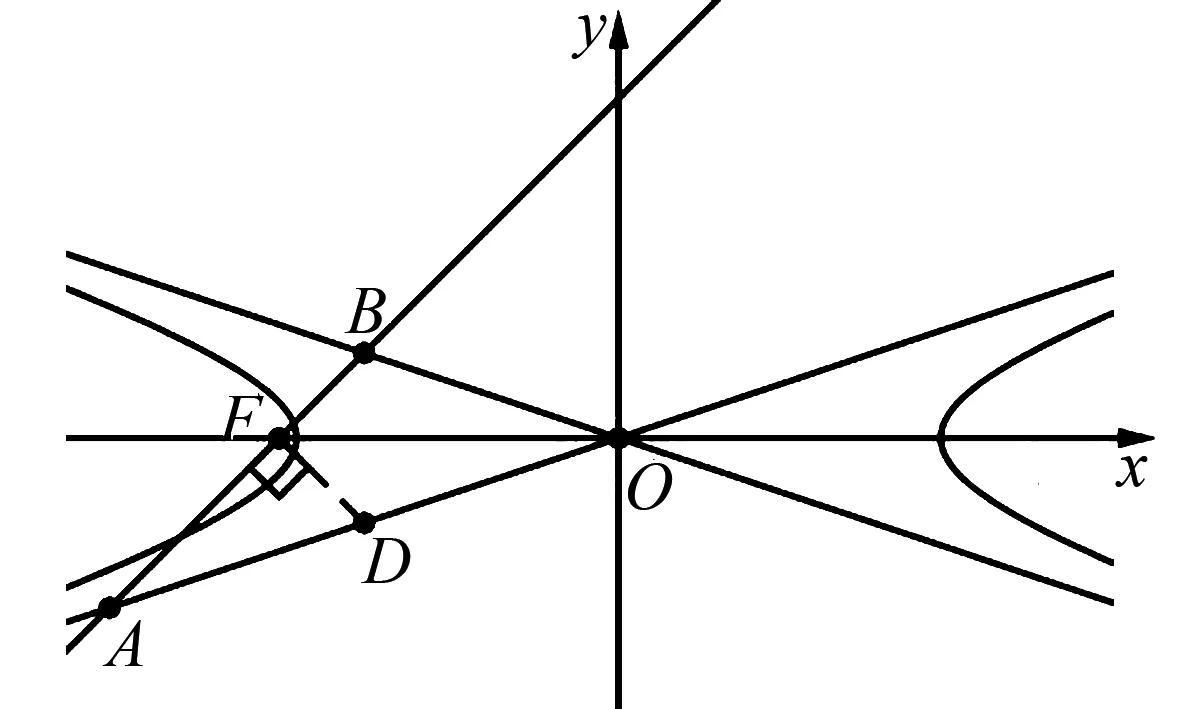
图4

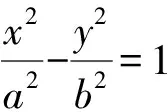
渐近线作为双曲线的重要性质，其相关问题蕴含了丰富的数形结合、等价转化的思想，对数学运算也有较高的要求，这就需要我们一方面要锻炼运算能力，总结运算技巧；另一方面要多对比一个问题的代数思路与几何思路的差异，关注不同方法运算复杂程度的区别，选择合适的方法来针对性解决相关问题.