对一道解析几何题的多角度探究

钟国城

(广东省梅县东山中学 514017)

1 试题呈现

(1)求C的方程;

(2)如图1,已知点F(1,0),直线l:x=4与x轴交于点D,直线AM与l交于点N,是否存在常数λ,使得∠MFD=λ∠NFD?若存在,求λ的值;若不存在,说明理由.

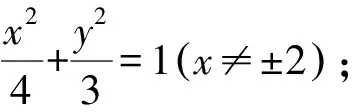
2 解法探究

分析1将角转化为向量夹角,通过数量积表示出来,实现角度的数量化,进而实现坐标化,从而达到解决问题的目的.

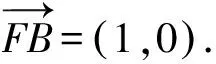
设N(4,n)(n≠0),

图1

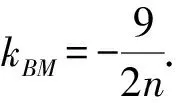
故直线AM与BM的方程分别为

即∠MFN=∠NFB=∠NFD.

故∠MFD=∠MFN+∠NFD=2∠NFD.

因此存在常数λ=2,使得∠MFD=2∠NFD.

点评通过充分挖掘题设条件,联立两直线方程求解点M的坐标是一个亮点,既避免了繁杂的运算,又让求解过程显得更为自然.

分析2考虑与角关联的直线及其倾斜角,将角度关系转化为关联直线倾斜角之间的关系,进而通过使用斜率来求解问题.但需讨论倾斜角为90°的情况.

由于对称性,只需考虑点M在x轴上方的情况.

故∠NFD=45°.

所以∠MFD=2∠NFD.

因此λ=2.

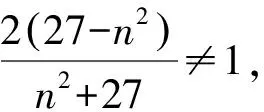
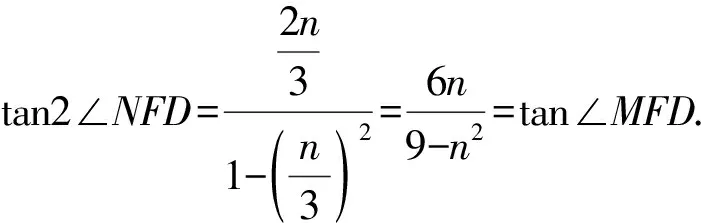
所以∠MFD=2∠NFD.因此λ=2.

综上,存在常数λ=2,使得∠MFD=2∠NFD.

分析3将∠MFN表示为∠MFD-∠NFD,从角关联的直线及其倾斜角入手,利用斜率与两角差的正切公式,找到∠MFN与∠NFD的关系,进而得到∠MFD与∠NFD的关系,从而求解问题.

由于对称性,只需考虑点M在x轴上方的情况.

故∠NFD=45°.

所以∠MFD=2∠NFD,因此λ=2.

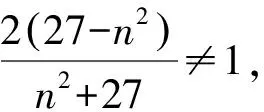
故∠MFN=∠NFD.

则∠MFD=∠MFN+∠NFD=2∠NFD.

因此λ=2.

综上,存在常数λ=2,使得∠MFD=2∠NFD.

分析4 通过特殊情况对题目进行分析,可以猜测λ=2,即∠MFN=∠NFD,从而只需说明直线NF为∠MFD的角平分线,因此考虑使用角平分线逆定理来求解问题.

直线BM与NF的方程分别为

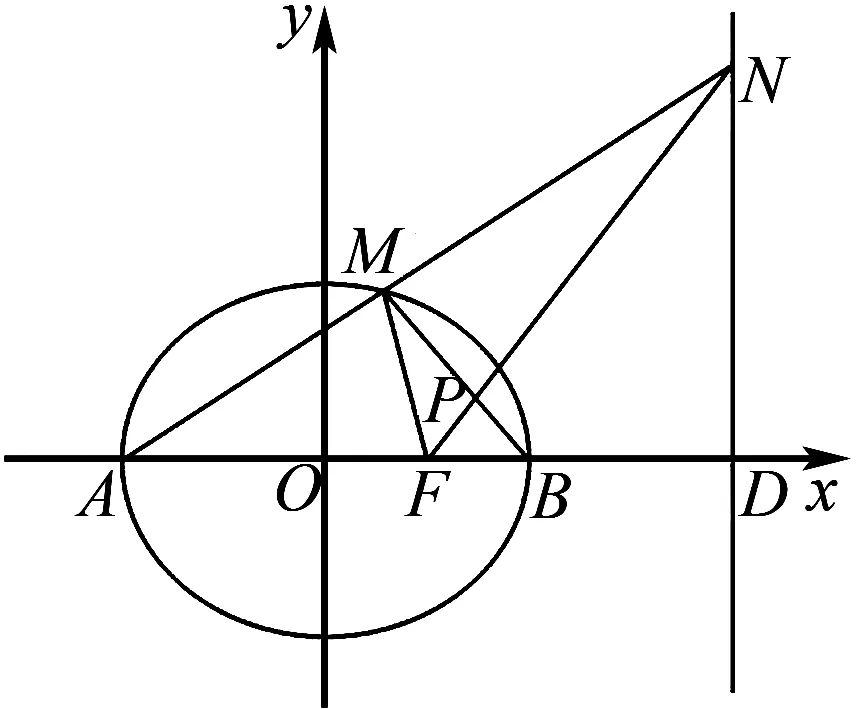
图2

设直线BM与NF的交点为P，如图2.

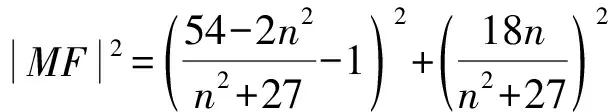
由角平分线逆定理,得∠MFN=∠NFD.

则∠MFD=∠MFN+∠NFD=2∠NFD.

因此,存在常数λ=2,使得∠MFD=2∠NFD.

分析5根据分析4,也可采用角平分线性质逆定理来解决问题.

故直线MF的方程为6nx+(n2-9)y-6n=0.

如图3，点N到直线FM的距离为

图3

因为点N到直线FD(即x轴)的距离为d2=|n|,所以d1=d2.

由角平分线性质逆定理,得∠MFN=∠NFD.

则∠MFD=∠MFN+∠NFD=2∠NFD.

因此,存在常数λ=2,使得∠MFD=2∠NFD.

分析6如图4，过点M,D分别作NF的垂线,构造两个直角三角形.通过证明这两个直角三角形相似,得到∠MFN=∠NFD,从而求解问题.

直线NF的方程为nx-3y-n=0.

所以点M与D到直线FE的距离分别为

图4

如图4，过点M与D分别作MQ⊥NF于点Q,DS⊥NF于点S,则|MQ|=d,|DS|=d′.

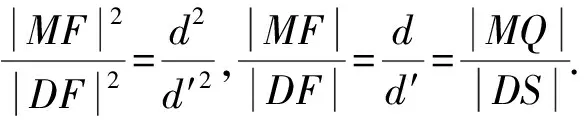
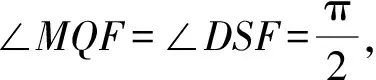
所以Rt△MQF∽Rt△DSF.

故∠MFQ=∠DFS.

即∠MFN=∠NFD.

则∠MFD=∠MFN+∠NFD=2∠NFD.

因此,存在常数λ=2,使得∠MFD=2∠NFD.

分析7从对称的角度入手,如图5，若点D关于直线NF对称的点在直线MF上,则∠MFN=∠NFD,最终解决问题.

直线NF的方程为nx-3y-n=0.

设点D关于直线NF对称的点为D′(x0,y0),

图5

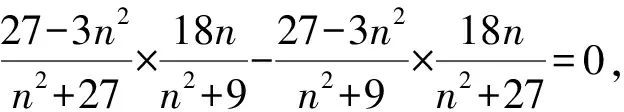
即F,D′,M三点共线.

故∠MFN=∠NFD.

则∠MFD=∠MFN+∠NFD=2∠NFD.

因此,存在常数λ=2,使得∠MFD=2∠NFD.

分析8由于题设条件涉及到右焦点与右准线,利用椭圆的第二定义,结合平行、相似等平面几何知识,找到相关的几何性质与关系,从而求解问题.

图6

解法8如图6,过点M作MG⊥l于点G,交NF于点E.

由于直线l:x=4为椭圆的右准线,根据椭圆的第二定义,得

由MG∥AD,得

所以|ME|=|MF|.

故∠MFE=∠MEF=∠EFD.

故∠MFN=∠NFD.

则∠MFD=∠MFN+∠NFD=2∠NFD.

因此,存在常数λ=2,

使得∠MFD=2∠NFD.

3 试题推广

通过对第(2)问的求解,笔者发现可将其作进一步延伸,经过整理得到如下几个结论.

由椭圆类比双曲线、抛物线,也有一致结论.

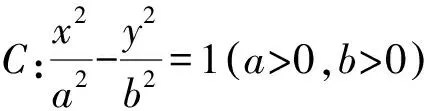
参照试题第(2)问的求解,读者不难验证命题1-5的正确性,此处从略.

4 解题反思

4.1重视一题多解,提升学生思维

在平时解题教学中,不仅要帮助学生解决问题,更要教会学生从多个视角进行分析,注重知识点之间的相互联系,做到融会贯通,这对于培养学生的数学思维能力能起到潜移默化的作用.如本试题的解决,联系了向量夹角、直线倾斜角与斜率、两角差的正切公式、角平分线、对称与三点共线,以及椭圆的第二定义等相关知识,既让学生掌握了基础知识,又有效锻炼了学生思维的深刻性、广阔性、灵活性和创新性,提升思维能力.

4.2 挖掘问题本质,以求触类旁通

我们不仅要注重一题多解,更要对典型问题进行深度探究,挖掘问题的本质,并进一步做出一般化的推广.如通过对本试题的研究,找到了一般化的结论,既发挥了题目的最大价值,更能让学生“做一题,会一类”,让学生跳出题海战术,减轻学习负担,提高学习效率,从而达到举一反三、触类旁通的解题水平和能力,进一步掌握数学思想,提升数学核心素养.