高中数学解题技巧分析

杨曼 付苗苗

【摘要】为提升学生的数学核心素养和数学解题能力，文章对高中数学解题技巧的对策进行深入分析，结合具体例题，从在解题方法全面透析、科学转化数学问题、通过图像探析问题本质、注重学生分析思维能力培养、强化学生知识反思与总结五个方面对学生的数学解题技巧的提升路径进行详细阐述.

【关键词】高中数学；解题技巧；培养策略

引 言

高中数学解题难度较大，且解题路径较多，需要学生掌握多样解题方法与技巧，在提升解题效率与精准性的基础上，实现数学核心素养的发展.但在实际教学过程中，通常存在学生掌握解题技巧不熟练、不全面等问题，这不利于学生解题能力的提升.据此，文章以提升数学解题效率与精准性为目标，提出高中数学解题技巧的对策，旨在为提升学生数学解题技巧，丰富学生数学解题方法体系，实现学生解题能力提升提供参考与借鉴.

一、解题方法全面透析

对数学问题进行全面透析是提升学生解题综合成效的关键所在，是推动学生解题能力高质量发展的重要落脚点.从整体视角来看，部分教师在开展教学实践活动过程中将题目分析与讲解视为教学核心内容，没有有效推进学生思考，忽视了题目与解题方法之间的关联性，这不利于激发学生的解题兴趣，难以有效提升学生的解题效率.对此，高中数学教师应转变教学重点，注重解题方法的全面透析与讲解，促使学生在分析题目过程中快速找到解题方法，并在提升解题技巧、解题能力的基础上实现数学核心素养的高质量发展.需要注意的是，解题方法的全面透析不仅仅是解题思路的透析，需要教师将数学基础知识进行链接，帮助学生构建完整的解题知识体系，锻炼学生的逻辑思维，助力学生的解题思维和能力的发展.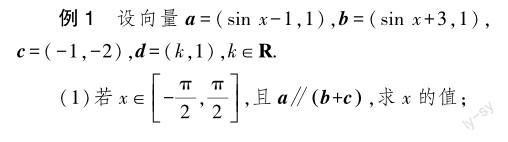

教师在带领学生读完题目后，引导学生对（1）内容进行分析，并明确（1）的解答需要应用向量的共线的坐标表示及三角函数的图像和性质.基于此，分析（2）发现，该问题的解答需要运用向量的垂直的条件，以及参数分离和正弦函数的值域.在分析过程中，教师应帮助学生厘清解题思路，并写出完整的解题过程.

通过解题方法的透析，学生可以有效把握解题的思路与解题路径，掌握解题技巧，构建思维体系.

二、科学转化数学问题

为有效帮助学生灵活掌握解题技巧，提升学生的解题能力，高中数学教师应注重引导学生转化數学问题.一方面，高中数学问题有一定难度，学生在解题过程中容易进入解题误区，从而无法有效解答题目；另一方面，高中数学问题具有巧妙性、系统性，一个数学问题可以通过多样化解题方式进行解答.为帮助学生有效转化数学问题，数学教师应对学生情况进行综合分析，了解学生掌握、应用数学解题方法的实际情况.基于此，高中数学教师应积极引导学生以简便的方式，将复杂的数学问题进行转化，以提升学生数学问题解答实效，促进学生数学思维能力的发展.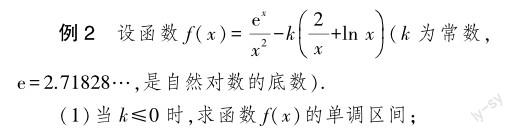

（2）若函数f（x）在（0，2）内存在两个极值点，求k的取值范围.

在引导学生对上述题目进行解答的过程中，教师可以引导学生对题目内容和问题内容进行思考，以提问的方式为学生设置思考切入点.如提出问题：“本题目的问题（1）和问题（2）是否可以用其他的数学形式进行解答？”通过思考问题，学生快速转变思维方式，明确了本题目可以应用不等式相关知识进行解答.在学生思考后，数学教师引导学生共同完成解题过程.

数学问题的转化，不仅简化了数学问题，提升了数学问题解答实效，更为学生提供了更多的问题解答切入点，促使学生能够充分利用已学知识解答多类型的数学问题，为学生的数学解题能力提升、数学思维及核心素养发展助力.

三、通过图像探析问题本质

通过图像探析问题本质是解答数学问题的有效方式与路径.在利用图像分析数学问题的过程中，学生可以将复杂的数学问题转化为具体的图形，这有利于学生对数学问题进行深入分析和解答，对提升学生数学问题解答效率与质量具有积极作用.同时，在根据题目信息建立图像的过程中，学生可以对数学问题进行深入分析，快速提取解答问题所需的基础知识内容，从而提升问题解答精准性.为帮助学生掌握图像解析数学问题的方法，高中数学教师应在讲解数学题目过程中引导学生根据数学题目信息绘制图像，并找出解题切入点，助力学生思考与解答数学问题.在实际数学问题解答过程中，学生一般会遇到两种情况：第一种情况，题目未给出图像，需要学生自行绘制；第二种情况，题目给出了相应图像，需要学生进行进一步绘制和分析.对此，下文分别列出两种情况的问题解答过程.

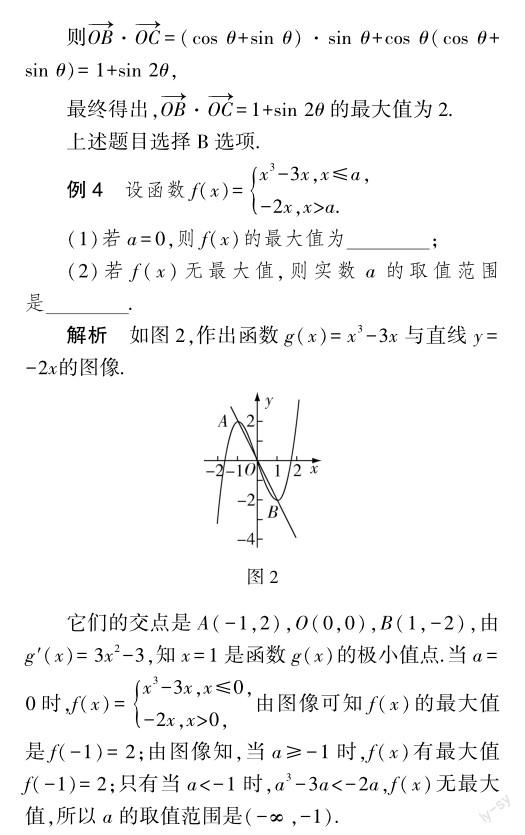
基于此，教师应指导学生明确：求分段函数的函数值时，应先确定所给自变量的取值属于哪一个范围，然后选取相应的对应关系.若自变量的值为较大的正整数，一般可考虑先求函数的周期；若给出函数值求自变量的值，应根据每一段函数的解析式分别求解；在研究函数的单调性时，需要先将函数转化为函数单调性问题，以提升解题效率.

通过图像解析，学生快速找到问题的本质，有效提升了解题效率与质量，这对拓展学生的解题思维，发展学生的数学素养能力具有积极作用.

四、注重学生分析思维能力培养

良好的分析思维能力是高中生有效解答数学问题的基础与前提.为有效培养学生的分析思维能力，高中教师应注重引导学生发散思维，通过帮助学生整合解题思路等方式，使学生建立完整的解题思维体系，提升问题分析能力和解题能力.

五、强化学生知识反思与总结

强化学生知识反思与总结是有效提升学生解题能力的路径与方式.在具体教学实践中，教师应注重指导学生在其解答完问题后，对解答方法的有效性、全面性，解题过程的简便性、规律性等进行思考.同时，教师应引导学生对解题过程中遇到的数学知识进行分析和总结，为后续问题解答奠定良好的基础，最终实现学生解题思维能力和数学核心素养的提升.

結 语

综上所述，高中数学的解题过程烦琐，且题目较复杂，含有多项误导信息，为有效培养学生的数学解题技巧及能力，教师应注重引导学生形成数学解题思路.在具体教学实践中，教师应引导学生对数学问题解答方法进行全面分析，并着重掌握图形转换方法、图形解析方法，以提升解题效率与精准性.在此基础上，教师应引导学生对解题知识进行反思和总结，促使学生逐渐构建完整的数学问题解题体系，助力学生发展解题能力，提升数学核心素养.

【参考文献】

[1]谢玉龙，杨爱玉.高中数学函数解题思路多元化的方法[J].亚太教育，2022（19）：135-137.

[2]林巧攀.高中数学解题过程中学生反思能力的培养策略[J].亚太教育，2022（12）：133-135.

[3]舒华瑛.转化与化归思想在高中数学解题教学中的应用研究[J].延边教育学院学报，2021，35（6）：190-195.

[4]吴玉辉.构造法在高中数学圆锥曲线解题中的应用[J].华夏教师，2021（35）：31-32.

[5]舒华瑛.高中数学解题教学中学生高阶思维能力的培养：以恒成立求参数问题为例[J].延边教育学院学报，2021，35（5）：205-209，214.