结合关系路径与有向子图推理的链接预测方法

马 力，姚伟凡

西安邮电大学 计算机学院，西安710061

知识图谱（knowledge graph，KG）是用来存储由实体及其关系组成的事实三元组的知识库，如FreeBase、DBpedia、Wikidata 等都属于大规模的知识图谱。知识图谱在智能问答[1]、推荐系统[2]、搜索引擎[3]等各行各业都有广泛的应用。如小米知识图谱[4]，已支持其每天亿级的访问，用于其智能问答、用户画像、虚拟助手、智能客服等互联网产品。大型的KG含有数十亿个三元组，但由于人类知识、网络语料库不断更新和提取算法的限制，即使是最大的知识库也仍然不完整。如在FreeBase 中300 万个人实体中有75%没有国籍。为了解决这一问题，Bordes 等人提出了经典的Trans E 模型[5]，一种基于KG 嵌入的表征学习，而后研究者们相继提出Trans D[6]和Trans R[7]等模型。该方法旨在将KG 的实体和关系嵌入到连续的向量空间中，同时保留KG 的固有结构和潜在语义信息。如图1 所示，哈利·波特的嵌入包含他是格兰芬多学院的学生以及格兰芬多学院的一部分信息，基于词嵌入的方法可以检索这些信息来预测罗恩和哈利·波特是同学，任何一个和格兰芬多学院关系密切的人都会大概率属于霍格沃兹学校，这些都可以在嵌入空间中进行编码。这种方法的优势在于，它们考虑了KG 中给定实体的结构上下文，但它们无法捕捉头实体和尾实体之间的多种关系（路径），而这对于KG 的完成非常重要，并且该方法不能有效地捕捉知识图的关系语义，即知识图底层关系中的逻辑规则。

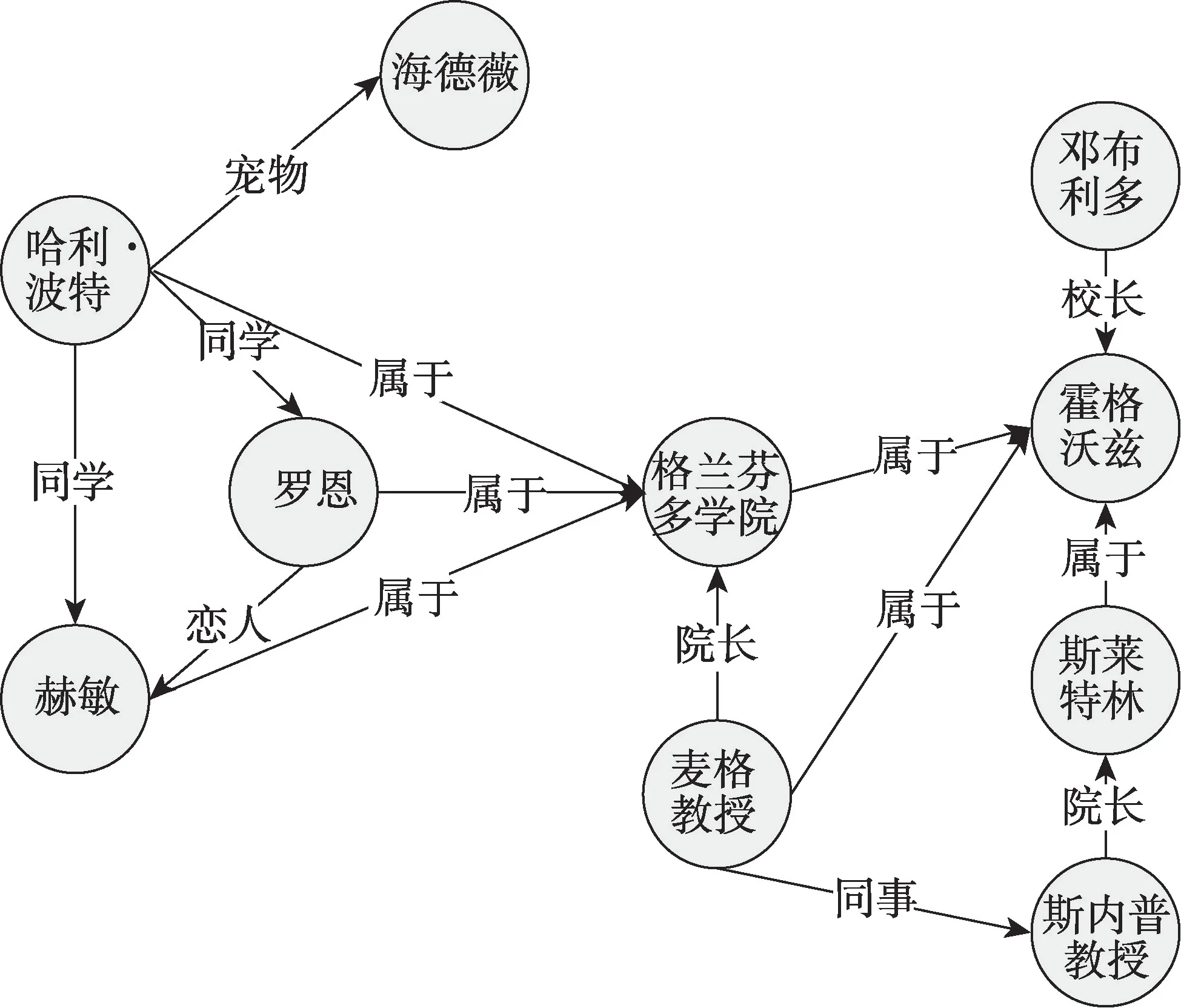
图1 基于嵌入式的关系预测推理方法Fig.1 Relationship prediction reasoning method based on embedded system

第二类方法是基于规则的[8]方法，考虑到逻辑规则的准确性和可解释性，在KG 嵌入中应用额外语义信息的一个有效方法是使用逻辑规则。其目的是通过对头部和尾部实体之间的路径进行建模，从KG 中学习一般的逻辑规则。还有一种方法利用知识图谱中频繁共现模式确定逻辑规则[9]，基于逻辑规则学习的链接预测方法的一个主要优点是它们可以应用于直推和归纳问题。然而，这些方法也存在一定的缺陷，有意义的规则通常非常少，影响了该方法预测已知规则未涵盖的缺失关系的能力。而关系预测任务也可以被视为一个逻辑归纳问题，在这个问题中，研究者们试图推导出一个给定KG 的概率逻辑规则（horn 子句）。如从图1 所示的知识图谱中，可以推导出简单的规则，如式（1）所示。

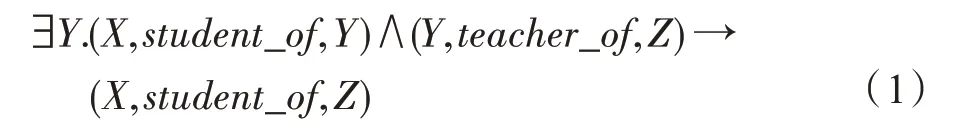
其规则可以预测这种关系，如图2 所示的例子。虽然基于嵌入的方法将实体特定的邻域信息编码到嵌入中，但这些逻辑规则捕捉独立于实体的关系语义，学习独立于实体的关系语义具有归纳出看不见的实体的能力。式（1）中的规则可以推广到图2 中看不见的KG，并预测这种关系。本文学习根据候选关系周围的有向子图结构来预测关系,而不是学习特定于实体的嵌入。并且在这种方法基础上捕获两个实体之间所有路径的关系路径以提高模型预测已知规则未涵盖的缺失关系的能力。

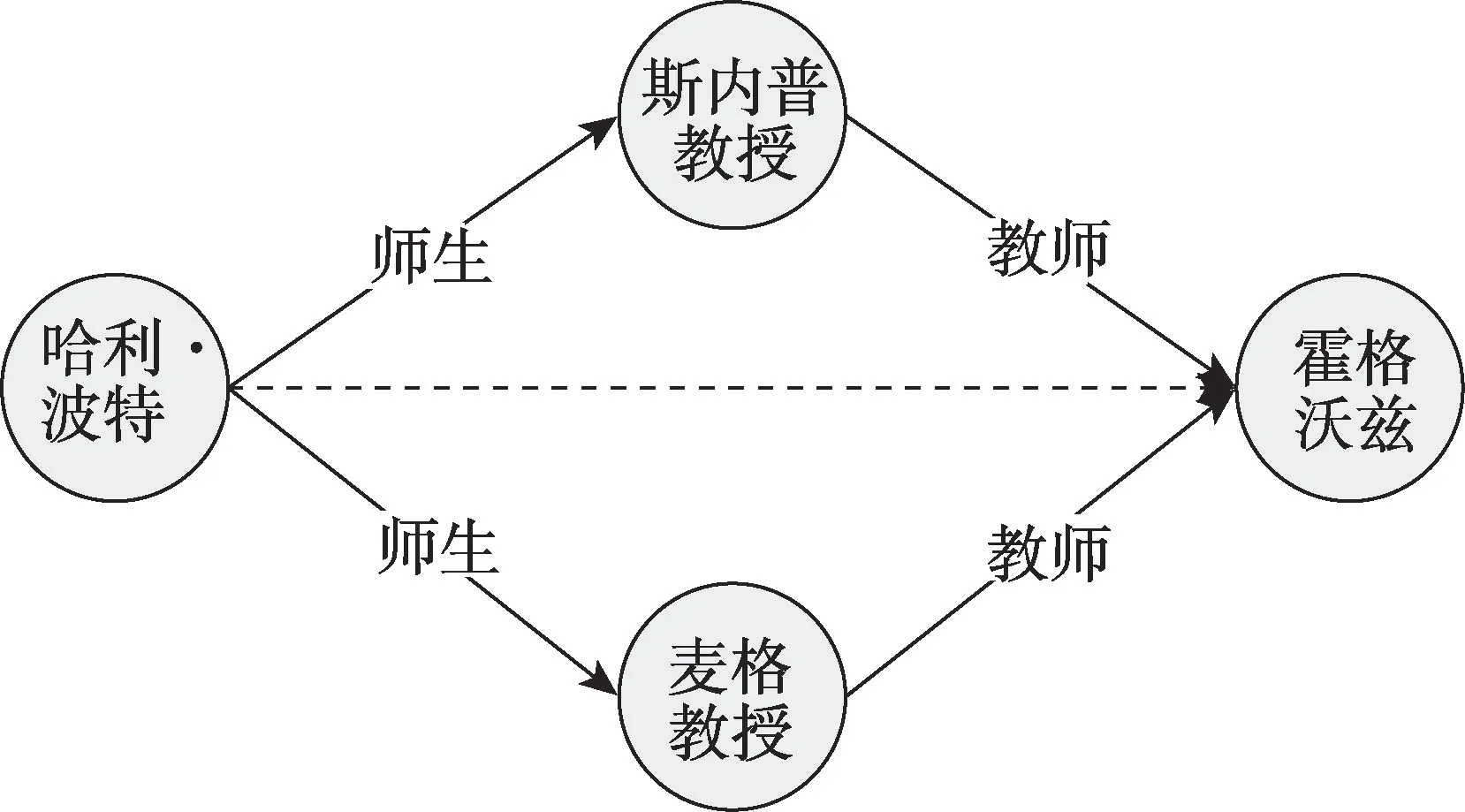
图2 基于规则归纳式推理方法Fig.2 Inductive inference method based on rules

1 相关工作

1.1 基于图神经网络的方法

大多数现有的知识图谱补全方法都是基于嵌入的方法，RotatE[10]、ComplEx[11]、ConvE[12]和TransE[5]等都是经典的基于嵌入的方法，但这些方法独立地处理每个三元组，而不考虑嵌入在丰富邻域中的语义和结构信息。近年来，图神经网络（graph neural networks，GNN）模型在知识图谱推理任务中都获得了经验性的成功。文献[13]通过引入算法对齐策略，将图神经网络与其他推理任务的解决算法进行对齐分析，证明了图神经网络模型的推理能力。现在图神经网络已被用于捕获固有地存储在KG 中的全局结构信息，并在各种数据集上得到了最佳结果[14-16]。文献[17]用图卷积网络（graph convolutional networks，GCN）引入一个局部敏感的嵌入，然后传入其解码器中预测图谱中丢失的连接。目前提出的这种方法本质上是直推式的，但如果给定一些节点特征，利用特征信息训练可以对未出现的顶点生成嵌入[18]，这种基于GCN 的知识图谱补全方法需要学习节点特定的嵌入。本文方法将关系预测视为一个子图推理问题，经过训练后可以推广到看不见的实体。

1.2 规则归纳方法

由于存在实体不可见的问题，基于规则归纳的知识图谱补全方法一直被限制，目前针对这个问题，文献[19-20]提出的方法可利用许多知识图谱中不存在的节点特征进行链接预测，文献[21]通过使用GNN聚合邻居节点嵌入，学习为看不见的节点生成嵌入，然而这两种方法都需要新节点被已知节点包围，并且不能处理全新的图。这些方法本质上是归纳性的，因为规则独立于节点身份，但是这些方法由于其基于规则的性质而受到灵活性问题的困扰，并且缺乏表达能力。与基于嵌入的方法不同，统计规则挖掘方法通过列举知识图谱中存在的规律和模式来归纳概率逻辑规则。在这些统计规则归纳方法的基础上，NeuralLP[22]、RuleN[23]和DRUM[24]提出以端到端的方式学习KG 中的逻辑规则和置信度得分，但它们没有考虑到预测关系周围的邻居结构，因此当头实体和尾实体之间的路径稀疏时不够表达。文献[25]提出一种基于图神经网络的关系预测框架GraIL（graph inductive learning），它对局部子图结构进行推理，并对学习独立于实体的关系语义有很强的归纳性。与基于嵌入的模型不同，GraIL 是自然归纳的，经过训练后可以推广到看不见的实体和图形，解决在知识图谱上进行归纳式关系预测的问题。

1.3 基于关系路径的方法

近年来研究者们通过探索知识图谱中实体间的连接，将实体间的连接发现为路径，关系路径揭示了实体和关系的语义。KPRN（knowledge-aware path recurrent network）[26]模型通过组合实体和关系的语义来生成路径表示，并在路径上进行有效推理。文献[27]通过可学习的注意力机制自适应地整合关系上下文和关系路径，与传统的基于节点的表示不同，该模型仅使用关系类型来表示上下文和路径，这使得它适用于归纳设置。本文方法利用一个归纳关系推理的消息传递神经网络，结合实体间的语义关系对局部有向子图结构进行推理，完成知识图谱补全任务。

2 算法设计

2.1 问题描述

一个新的实体加入到知识图谱中，规则在不再训练的情况下依然保持准确性。但基于规则归纳的链接预测方法由于其基于规则的性质导致其方法可扩展性差，缺乏表达能力，不能预测看不见的节点。GraIL 基于图形神经网络利用提取封闭子图的方法对在训练集中没有见过的实体进行关系预测，主要分为三个步骤，分别是：（1）子图采样；（2）节点初始化；（3）利用图神经网络进行消息传递和关系预测。但其也存在一定的缺点，如在提取目标三元组的封闭子图时，忽略了知识图谱的方向性，使得它不能有效地处理知识图谱中的二元关系，尤其是对于非对称的关系。对于这一问题，本文提出提取有向子图的方法使模型能够关注到知识图谱中关系的方向性，如图3 所示。其采用的消息传递机制削弱了关系嵌入的作用，没有注意到头部和尾部实体间的关系路径，而实体之间不同的连接路径揭示了它们关系的本质。这违反了归纳关系推理的本质，因为归纳设置是独立于实体的，并且依赖于关系信息进行推理。

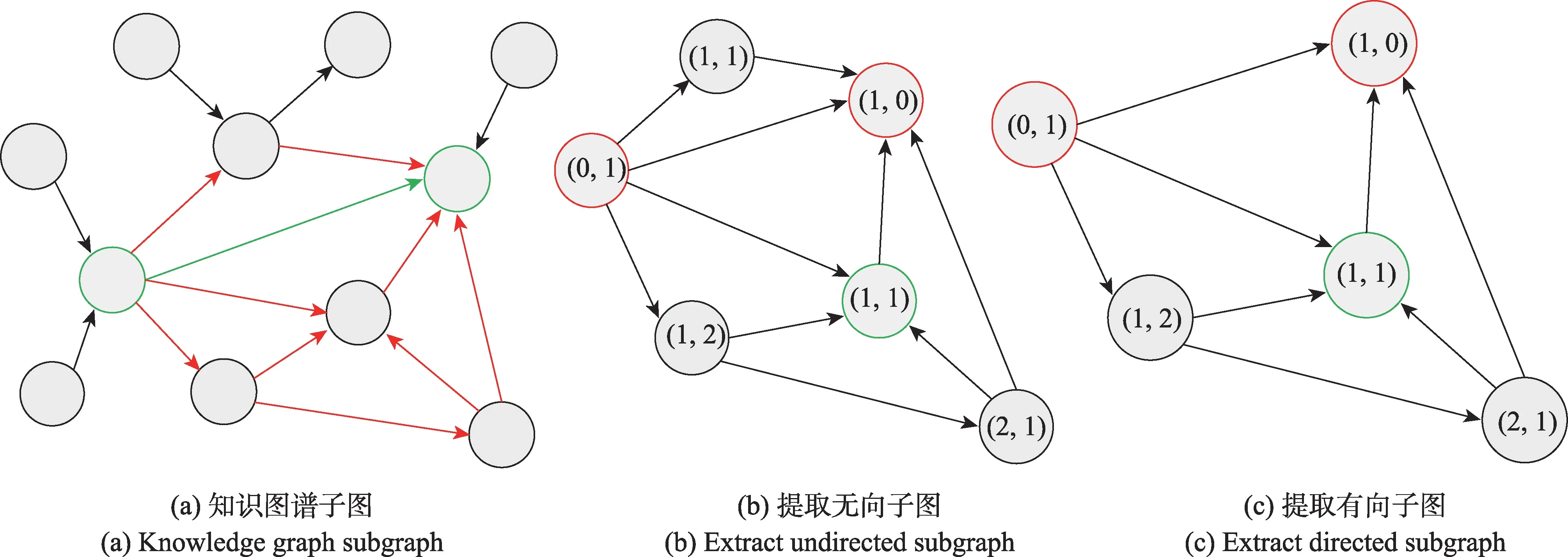
图3 提取无向子图和提取有向子图区别Fig.3 Difference between extracting undirected subgraph and extracting directed subgraph

2.2 处理思想

基于以上观察，本文提出了一种新的用于归纳关系推理的方法。在本文方法中，首先为每个三元组提取有向封闭子图，使其能有效地处理KG 中的非对称关系。利用边缘感知的注意力机制聚集局部邻域特征，并收集全局实体信息以丰富实体/关系表示，扩展其信息传递机制，以加强实体和关系之间的信息传递。同时更新边缘和实体嵌入，识别从头部实体到尾部实体的所有路径，每个路径都由其关系类型表示。如图4 所示。

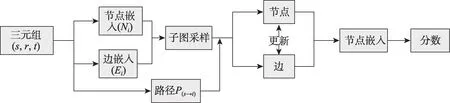
图4 节点-边双向信息传递模型框架图Fig.4 Framework diagram of node-edge bidirectional information transmission model

知识图谱中的目标三元组表示为(s,r,t)，其中s、r、t分别指头实体、关系和尾实体。归纳关系推理旨在对目标三元组(hT,rT,tT)的合理性进行评分，其中hT和tT的表示在预测期间不可用。在这项工作中，本文使用一个封闭的有向子图来表示目标三元组(hT,rT,tT)。目标头部和尾部之间的封闭子图表示为G=(V,E)，其中V和E∈V×V分别表示子图G中的节点集和观察边集。Ne表示子图中的边数，表示节点的嵌入，其中Nn是子图中的节点数。表示关系嵌入，其中Nr是通过梯度下降更新的一个可学习矩阵，在训练集和测试集中共享。将头节点到边、关系到边和尾节点到边的邻接矩阵定义为，目的是将头节点、关系和尾节点分别映射到相应的边，邻接矩阵中的值是0 或1，其中0 表示没有连接。

2.3 关键步骤

2.3.1 子图提取

在知识图谱中，假设预测目标节点之间的关系信息所需的逻辑规则存在于特定三元组的局部图邻域中，并假设两个目标节点之间的路径还包含其相关的关系信息。首先提取目标节点周围的封闭子图，同时考虑到三元组中存在的逻辑规则，提取带有方向性的图神经网络子图。在一个知识图谱中，存在三元组(hT,rT,tT)和(tT,rT,hT)，如果提取无向子图，对这两个三元组提取出的子图可能是相同的，但如果关系rt是非对称的，则这两个三元组中只有一个是真的。因此使用有向封闭子图处理这类关系。

假设存在一个三元组(s,r,t)，为使模型可以识别三元组中的方向性，将s定义为t的上一跳邻居，t定义为s的下一跳邻居，k定义为目标节点的前/后k跳邻居节点。假设用+表示方向向后，-表示方向向前。则第一步：提取满足s+k的节点和t-k的节点，提取满足t-1 的节点。如果s+k和t-1 之间存在共同的实体，则目标节点s和目标节点t之间存在有向子图。如果s或t不在公共实体中，则需要将它们添加到公共实体中。子图构造方式如图所示，通过这种方式，从目标头部到尾部的最大距离将变成k+1。

2.3.2 关系路径消息传递机制

在GraIL 模型中，消息传递模型是一个简单的带边注意力的R-GCN（relation-graph convolution networks），忽略了边与节点之间的双向信息传递。该模型使用节点到节点的消息传递机制，其中关系信息仅用于计算相邻节点的权重。但在归纳关系推理中关系起主导作用，而实体在推理期间不能提供确定性信息，节点到节点的消息传递机制削弱了关系的作用，违背了归纳知识图的本质。

在文献[28]的消息传递框架中，通过迭代和增强边与节点嵌入来建模归纳封闭子图。其关键思想是加强节点之间相互作用的信息，使图结构得到了更好的表示方式。其采用通信消息传递算法，该算法交互式地更新有向图结构中的节点和边消息，每个边的表示通过头节点嵌入和它的逆边来更新，其采用的CMPNN（communicative message passing neural network）信息传递机制如图5 所示。但这种节点更新方式不适用于子图提取的方法，并且它忽略了尾节点嵌入和关系嵌入的信息。本文采用一种新的节点-边缘通信机制，同时考虑了头部、关系和尾部来更新边缘嵌入。在本文的信息传递机制中，假设节点嵌入总共更新了l 次迭代。在每次迭代中更新节点嵌入信息时都会关注到边嵌入信息，如图6 所示。

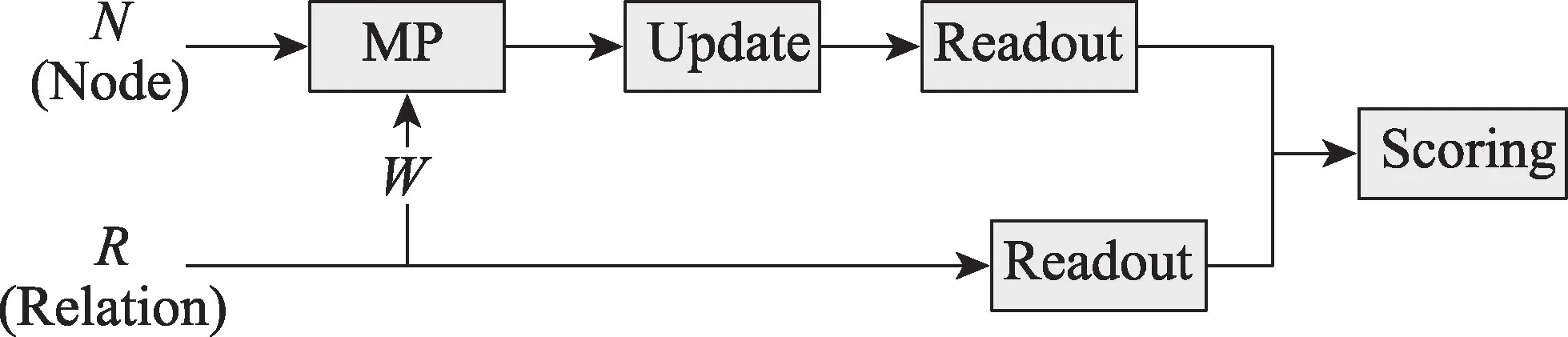
图5 CMPNN 信息传递机制图Fig.5 Mechanism diagram of CMPNN information transmission

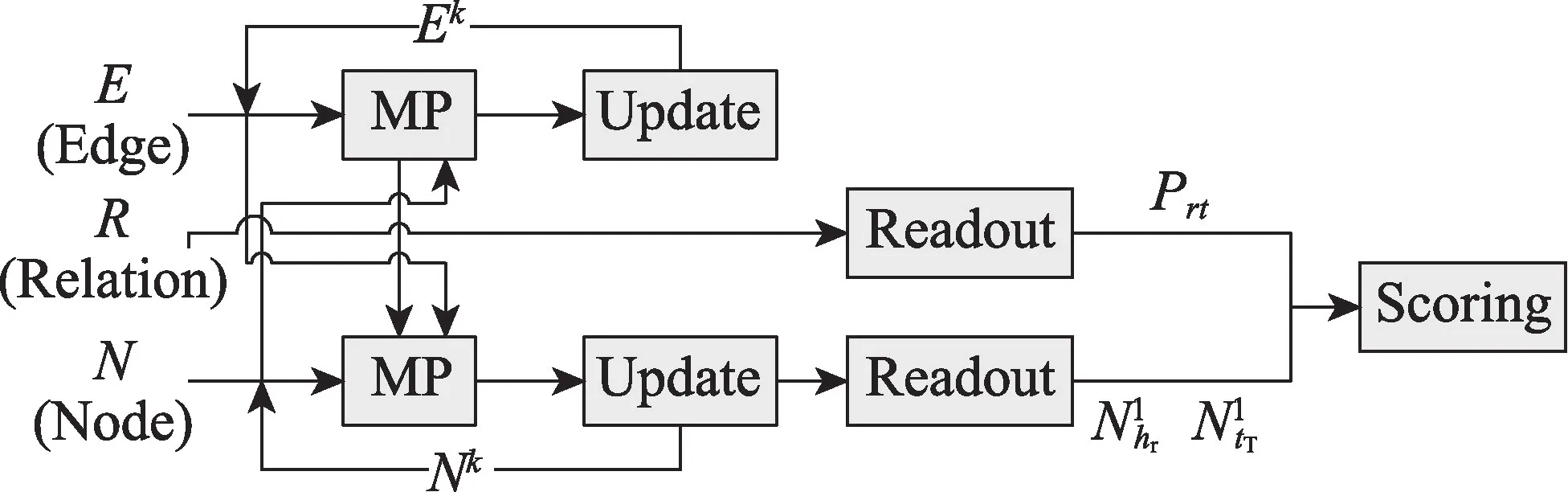
图6 节点边双向信息传递机制图Fig.6 Node side bidirectional information transmission mechanism diagram

在现在的消息传递机制中，没有考虑到节点标识，这导致了一个潜在的问题，即模型无法识别头s和尾t在KG 中的相对位置。如图7 所示，哈利·波特和海格之间的关系路径是（和，买，住在一起）。在图8 中，哈利·波特和赫敏·格兰杰之间的关系路径是（房子，房子）和（职业，职业）。其路径基于它们所包含的关系类型的顺序/结构来捕获（而不是基于实体的身份），训练期间不存在的新实体可以进入KG，对它们进行建模。基于s和t之间的连接模式，假设在KG 中从s到t的原始路径是实体和边的序列，其中两个实体vi和vi+1通过边ei连接，路径中的每个实体都是唯一的。对应的关系路径P是给定原始路径中所有边的关系类型的序列，即，其中，ri是边ei的关系类型。

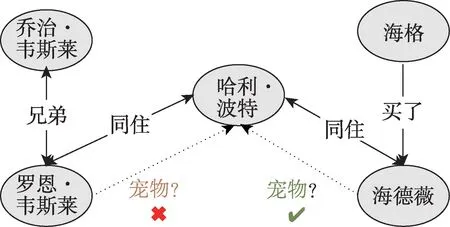
图7 相同关系路径实体关系背景不同Fig.7 Same relationship path and different entity relationship background

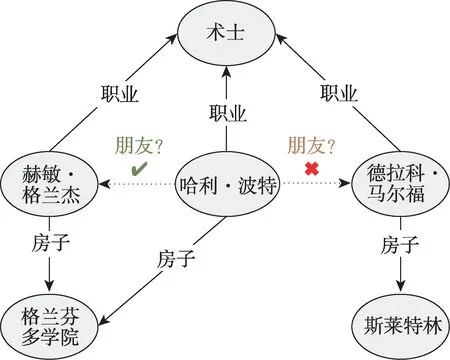
图8 相同关系语境的头部实体尾部实体路径不同Fig.8 Different head entity and tail entity paths with same relational context

首先将节点和边信息表示映射到相同的维度d，如式（2）所示。

2.3.3 节点嵌入更新

假设模型迭代k次，在每次迭代中，更新节点嵌入需要边缘嵌入。为了突出与目标三元组相关性高的边信息，本文使用一个边缘注意力机制。在GraIL的边缘注意力机制中，仅利用目标关系来预测边的重要性。本文利用所有的目标头、目标关系和目标尾来突出与目标三元组有密切联系的边缘。更全面地用整个三元组来引导注意力机制，因为节点可以在节点-边缘交互期间聚集关系信息，从而更新的节点嵌入也是有信息的。将Ps→t表示为KG 中从s到t的所有关系路径的集合。为每个关系路径P∈Ps→t分配一个独立的嵌入向量sP。不同路径的数量随着路径长度呈指数增长（存在|r|k-hop 路径），而在现实世界的KG 中，大多数路径实际上并不存在，例如长度为2 的所有可能路径中只有3.2%出现在FB15K 数据集中，因此在实验中对于相对较小的k值(k≤4)，不同路径的数量实际上是没有影响的。对于边i(1≤i≤Ne)，增强的边缘注意如式（3）～（5）：

在节点嵌入更新的最后一次迭代中，受文献[13]启发，使用多层感知网络，然后使用LSTM[29]代替式（7）以增加网络的表现力，如式（8）、式（9）所示：

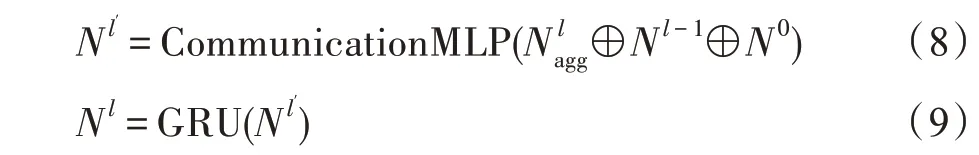
其中，CommunicationMLP 是传达节点聚合信息、节点嵌入和原始变换节点嵌入的多层感知网络，添加以执行残差学习[30]。边缘嵌入被更新为总共l-1 次迭代。为了更新边嵌入，在节点-边交互机制中需要节点嵌入，从节点到边的逆映射以及与边的关系如式（10）所示：

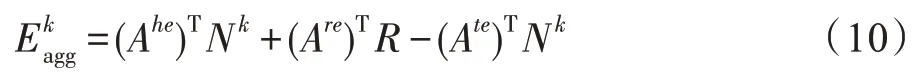
其中，T 表示矩阵转置，(Ahe)TNk将头部信息聚合到边缘，(Are)T将关系信息聚合到边缘，(Ate)TNk将尾部信息聚合到边缘，聚集边缘信息，并且在整个模型中保持一致。然后使用聚集信息来更新边缘如式（11）、式（12）所示：

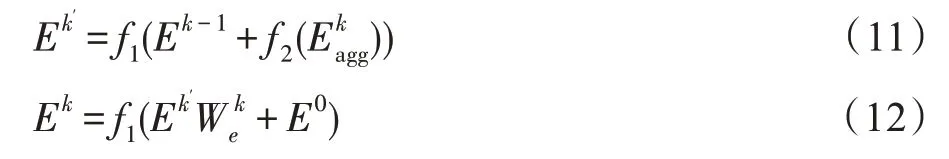
其中，f1和f2表示非线性激活函数。加入E0以更新等式中的边的嵌入。

2.4 评分函数定义

受GraIL 模型启发，本文使用非对称评分函数，该评价函数通过连接四个相关向量得到：

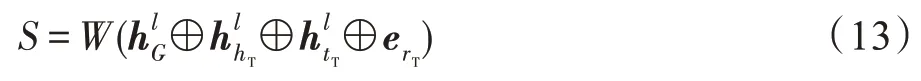
其中，表示子图表示，和表示头部和尾部实体的隐藏向量，erT是目标关系的学习嵌入。这个评分函数是对称的，因为关系嵌入和子图嵌入都是无方向的。为了缓解这个问题，采用了Trans E 的思想设计评分函数以保持模型的定向性，并与边信息的定义一致。评分函数定义如式（14）所示：

2.5 算法流程

假设对于两个需要被预测关系的目标节点（目标实体），它们之间的路径包含了被预测关系的信息。由于实体是不可见的，为子图中的每个实体（节点）定义一个独立于实体的嵌入。节点s和t周围的子图中的每个节点i用(d(i,s),d(i,t)) 标记，其中d(i,s)表示节点i和s之间的最短距离（同样对于d(i,t)），节点s到t的路径表示为Ps→t。整个方法流程如下：

3 实验

3.1 数据集

本文使用在链接预测任务中常用的三个大型数据集WN18RR、FB15K-237 和NELL-995 进行实验，为了便于归纳测试，通过从KG 中采样不相交的子图创建新的归纳基准数据集。每个数据集都由训练图和测试图组成，这两个图具有不相交的实体集合，训练图包含图中存在的所有关系。为生成训练图，用统一采样的几个实体作为目标节点，然后将目标节点周围的k跳邻域合并。并在每一跳上设置新邻居的数量，以防止指数增长。从整个图中删除样本训练图，并使用相同的过程对测试图进行采样。调整上述过程的参数得到一系列尺寸增加的图形，如表1所示。归纳设置中的模型在训练图上训练，在测试图上测试，随机选择测试图中10%的边/元组作为测试边。

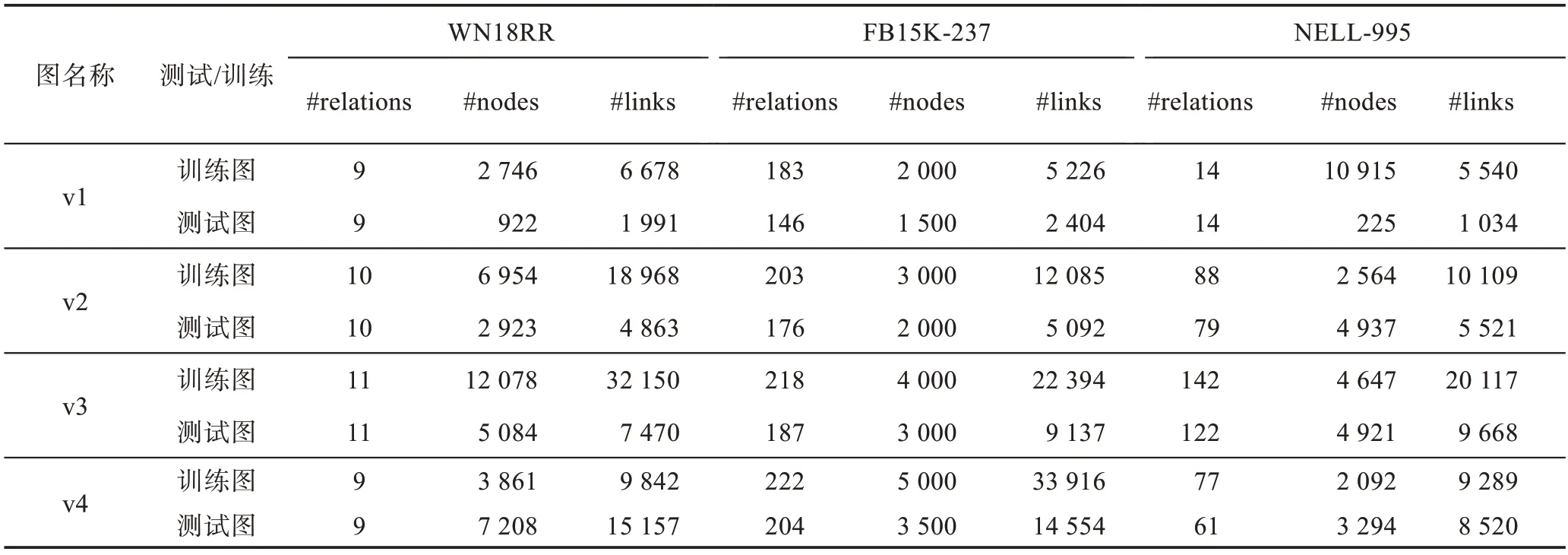
表1 数据集统计表Table 1 Statistical table of datasets

3.2 实验设计

本文使用AUC-PR 和Hits@10 评价指标，对测试集中的每个三元组都用无效实体替换三元组中的头实体或尾实体，产生一个无效三元组，并给每个三元组分配一个分数，用TransE 模型的实体和关系嵌入来初始化模型的嵌入。按照升序对这些分数进行排序，并得到正确的三元组的等级。在排序期间，移除已经存在于训练、验证或测试集中的无效三元组，通过替换尾部实体来重复整个过程，并评估哪个三元组得分更高以计算AUC-PR。将正三元组与采样的负三元组的得分进行比较，查看真实的三元组是否可以排在前10 位以计算Hits@10。对于原始归纳数据集，负三元组是随机抽样的，并且不考虑其是否具有封闭的子图。对提取的归纳数据集，使其确保负三元组也可以包含一个封闭的子图。

本文主要对比的三种基准模型分别是GraIL 与另外两种端到端可微方法Neural-LP 和DRUM 以及一种统计规则挖掘方法RuleN。就目前来说，Neural-LP 和DRUM 是能够进行归纳关系预测的可微方法，本文使用其提供的相同配置进行实验比较。RuleN代表了目前在知识图谱归纳关系预测方面的最新水平，RuleN 在归纳式场景下的推理方法在知识图谱补全任务中得到了很好的结果。RuleN 模型可以基于路径提取出知识图谱中的规则，本文使用RuleN 的原始术语，训练的学习长度设置为4，跳数设置为3。为保持公平的比较，在本文提供的模型中的目标链接的周围，抽取其3 跳封闭子图，使用一个3 层GNN，所有潜在嵌入的维数等于32。基准尺寸设置为4，边缘的dropout 设置为0.5。在本文实验中，Adam[31]优化器的学习速率设置为0.001，其他参数为默认值。margin 设置为10，Gradient 限制标准为1 000。模型在验证时进行评估，每3 个epoch 保存一次，使用性能最佳的点进行测试。模型的目标函数为S=。且模型根据需要自动调整每个节点的有效邻域大小。总共对模型进行4 次训练，并对测试结果求平均，以获得最终性能。

3.3 结果与分析

所有数据集测试集的预测结果如表2、表3 所示。本文使用公开可用的源代码，在数据集上复现了Neural-LP、DRUM、RuleN 和GraIL 模型的实验结果。最优的结果用粗体标出。

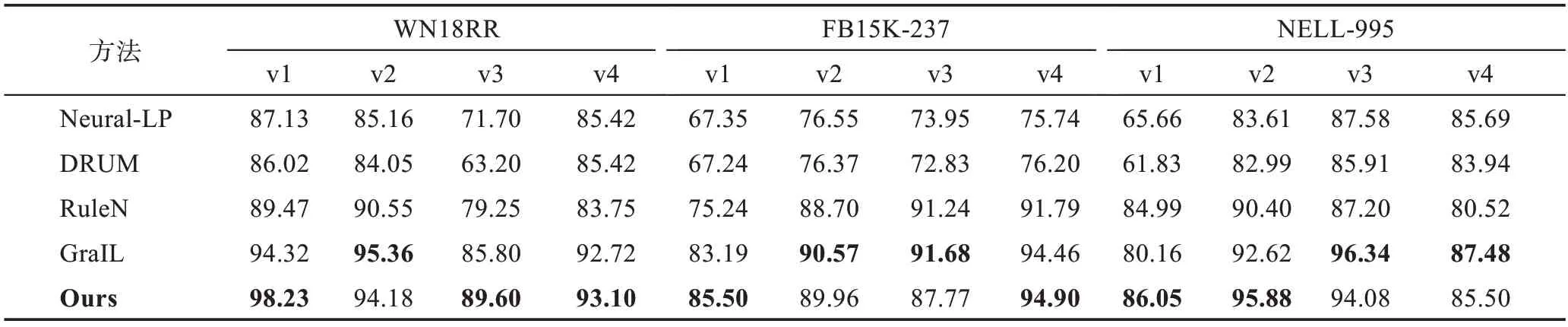
表2 AUC-PR 评价指标的实验结果Table 2 Experimental results of AUC-PR 单位：%

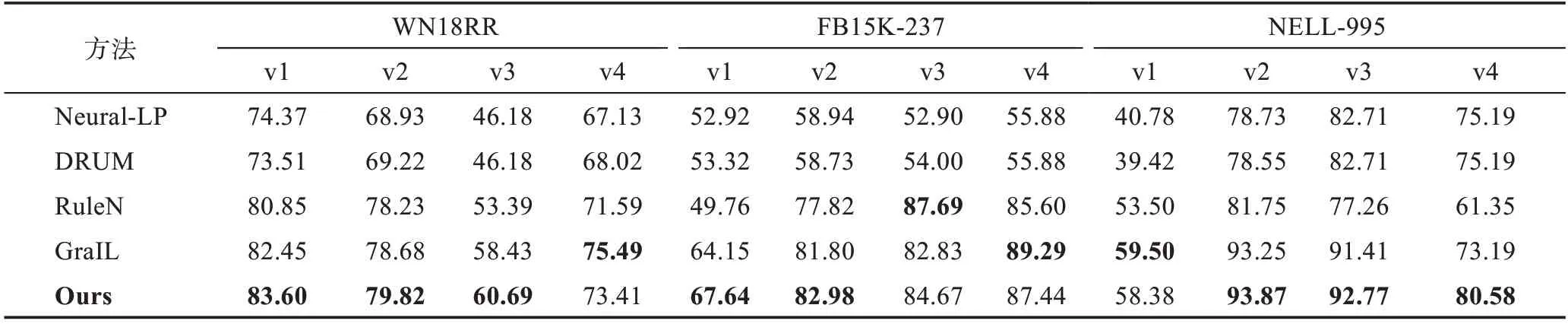
表3 Hits@10 评价指标的实验结果Table 3 Experimental results of Hits@10 单位：%

如表2 和表3 所示，在AUC-PR 评价指标上，相比基线模型，本文方法在WN18RR 数据集上的AUCPR 评价指标上有3 个数据集的结果都是最优结果，在FB15K-237 和NELL-995 数据集有两个结果都是最优。在Hits@10 评价指标上，相比基线模型，本文方法在WN18RR 数据集上的结果有3 个数据集的结果都是最优结果，在FB15K-237 有两个结果是最优结果，在NELL-995 中有3 个数据集的结果是最优结果。这表明了节点与边缘嵌入之间双向信息传递的必要性以及增强关系信息在网络中的作用的有效性。WN18RR 和NELL-995 是两个最稀疏的KG，在其数据集上的结果表明结合实体间的路径对于稀疏的KG 有着积极的作用。

3.4 有向路径子图与无向子图实验结果与分析

本文基于图神经网络提取有向路径子图进行链接预测，如果提取无向子图，对反对称关系的两个三元组提取出的子图可能是相同的，但这两个三元组中只有一个是真的。假设对于给定的实体对(h,t),h被名字、出生地、性别等包围，t周围是机构、地点、大学、创始人、大学校长等。则得出h很可能是个人，t很可能是大学，两者之间应该有一种毕业的关系，因为这样的模式在训练数据中经常出现。然而事实是，这个人与大学无关，出现这种错误的原因是忽略节点间的路径。因此本文使用有向路径子图处理这类关系。在实验中，对使用有向路径子图和无向子图的方法进行实验对比，结果如表4、表5 所示。

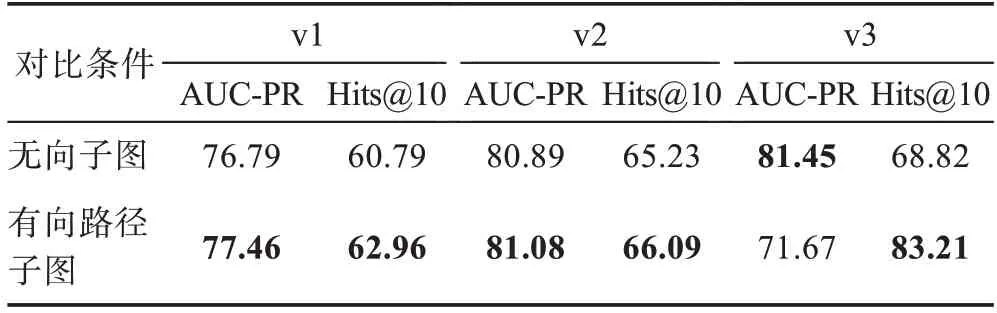
表4 FB15K-237 数据集无向和有向路径子图对比实验结果Table 4 Comparative experimental results of undirected and directed path subgraphs on FB15K-237 单位：%

如表4、表5 所示，当无向子图被有向路径子图代替时，就AUC-PR 和Hits@10 指标而言，有向子路径子图的方法结果明显优于无向子图的结果。这表明必须有效处理知识图中的方向问题，因为FB15K-237和NELL-995 都包含大量不对称和反对称关系。WN18RR 的改进相当显著，而WN18RR 是一个比较稀疏的数据集。这表明有向路径子图可以更好地推断两个看不见的实体之间的关系。

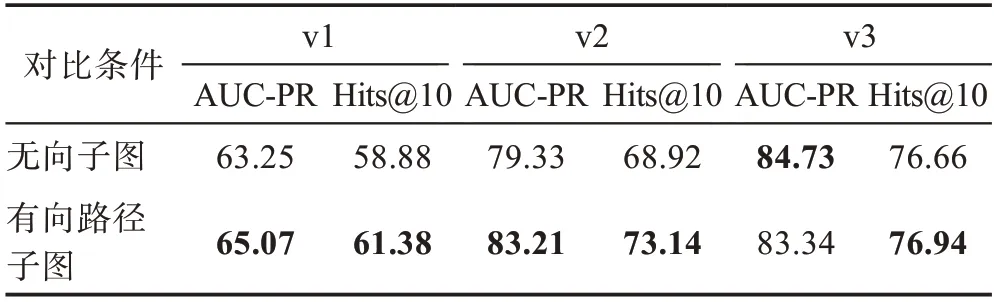
表5 NELL-995 数据集无向和有向路径子图对比实验结果Table 5 Comparative experimental results of undirected and directed path subgraphs on NELL-995 单位：%

3.5 消融实验

为证明本文方法每一步改进是否有效，对本文方法进行消融实验。针对本文中增强边缘注意机制的方法，将其从模型中移除并分析其结果。将增强的边注意机制与GraIL 中的边缘注意进行比较，GraIL 只使用目标关系引导边注意机制。本文还对边信息嵌入的更新是否会提高模型整体性能进行了实验，在嵌入更新时删除关系信息以及关系路径的实验结果如表6 所示。

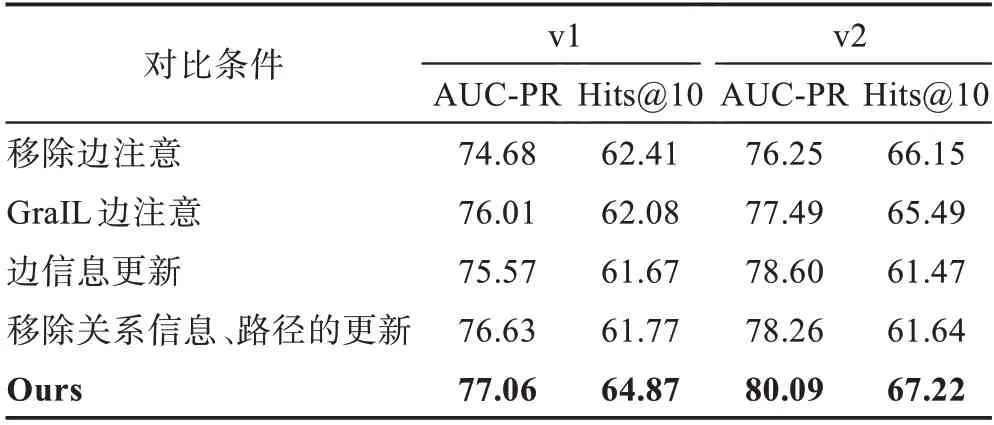
表6 消融实验结果Table 6 Results of ablation experiment 单位：%

如表6 所示，聚合边缘信息及路径的模型结果优于其他版本的模型。删除增强的边注意力的结果表明了增强的边缘注意力的有效性。增强的边注意力在FB15K-237-v1 数据集的AUC-PR 和Hits@10 度量上均提高了0.02 以上，并且在FB15K-237-v2 数据集上，即使没有边注意的模型也优于具有边缘注意的基准模型。这些结果表明，考虑目标三元组中的所有信息以确定哪些边是重要的具有重要意义。删除边信息更新模块后，所有评估指标上的性能都有所下降。与完全删除边缘嵌入更新模块相比，在边嵌入更新中删除关系信息及路径得到的结果改进较小，比呈现相关信息的情况弱。这些结果表明，边嵌入更新模块有助于本文方法对链接预测的重要性，并且关系信息在边嵌入更新中起着非常重要的作用。进一步证明了关系在归纳设置中的重要性，并强调了在子图建模中加强关系信息流的必要性。

3.6 非对称关系实验结果与分析

为证明模型可以在一定程度上处理非对称/反对称关系（通过使用特定的评分函数和边定义等），选择5 个不对称的关系来评估模型和基准模型GraIL。使用两种负三元组抽样策略：第一种是将其他三元组替换为正三元组的头或尾的标准操作；第二种是交换测试三元组的头和尾。结果如表7 所示。

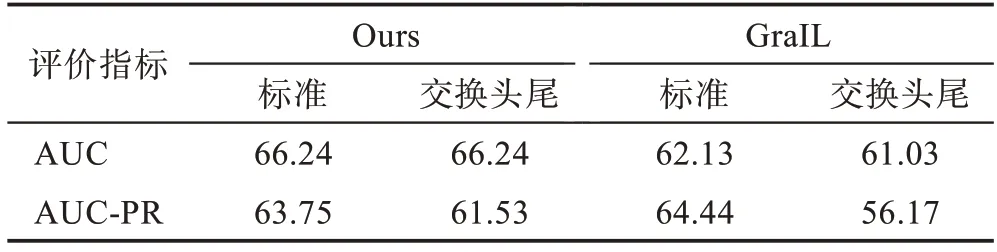
表7 非对称关系实验结果Table 7 Experimental results of asymmetric relationship单位：%

如表7 所示，模型使用标准方法和交换头尾方法的AUC 分数没有明显差异，这表明模型可以有效地将假三元组(t,r,h)与真正的三元组(h,r,t)区分开。相比之下，当样本策略更改为第二种策略时，基准模型GraIL 的比率有所下降，这表明本文方法有效地处理了KG 中的方向问题。

4 结束语

本文提出了一种用于归纳关系预测的有向路径子图推理方法，使用有向子图结合目标节点的关系路径推断两个不可见实体之间的关系。本文引入了一个新的消息传递模型，以学习更好的节点和边缘嵌入，并加强关系信息的作用。捕捉头实体和尾实体之间的关系路径，提高了三元组的预测精度。实验表明，本文方法在大多数评估指标上优于最先进的方法。在未来的工作中，也将尝试开发一个完全丢弃封闭子图中节点的纯关系消息传递网络，并研究关系封闭子图的性能。