自适应融合邻域聚合和邻域交互的图卷积网络

富 坤，禚佳明，郭云朋，李佳宁，刘 琪

河北工业大学 人工智能与数据科学学院，天津300401

现实生活中，存在大量不具备层次结构的关系型数据，例如城镇之间的交通线路、论文之间的引用关系以及商品之间的购买联系等，它们以图的形式存储在计算机中。这些图数据有复杂的结构和多样化的属性类型，能适应多领域的学习任务。近些年随着图的规模逐渐扩大，图数据的高维性和稀疏性越来越强，为了充分利用图数据的优势，出现了一类数据表示方法——图表示学习。图表示学习的目标是最大限度地保留图中节点的内容和结构信息，学习节点低维、稠密、实值的向量表示，给予下游任务（例如链接预测[1-2]、节点分类[3-4]和推荐系统[5-6]等）高效的数据支持。

目前图表示学习方法大体可分为两类：

第一类是基于简单神经网络的方法，包括DeepWalk[7]、Planetoid[8]等。DeepWalk首次将深度学习中神经网络概念引入图表示学习领域，它将图中的节点当作词，图上随机游走（random walk）生成的节点序列当作句子，从而类比词表示学习算法Word2vec，学习节点嵌入表示。Planetoid 在学习过程中融入标签信息，同时预测图中的类标签和邻域上下文进行图表示学习。尽管上述基于简单神经网络的方法实践效果很好，但是不能很好地反映邻域相似性。例如，DeepWalk、Planetoid 假设游走序列中相邻节点的嵌入表示相似，这种假设在游走次数极限形式下是正确的，但是在游走次数较少时算法低效。

第二类是基于图卷积神经网络（graph convolutional neural networks，GCNN）的方法，包括SCNN（spatial convolutional neural network）[9]、Chebyshev[10]、图卷积网络（graph convolutional networks，GCN）[11]、SGC（simplifying graph convolutional networks）[12]等。Bruna 等人[9]首次考虑对卷积神经网络进行泛化来适应非欧几里德结构的图数据。他们根据卷积定义方式的不同将GCNN 分为：（1）基于频域（或称为谱域）的GCNN，借助图的谱理论在频域上实现拓扑图上的卷积操作；（2）基于空域的GCNN，直接将卷积操作定义在每个节点的连接关系上；同时他们提出SCNN 算法，该算法的中心思想是：通过拉普拉斯矩阵的特征分解，得到可参数化的对角矩阵来替代频域中的卷积核。上述SCNN 算法要学习的参数量与图中节点数成正比，算法的时间复杂度为O(N3)，在图的规模较大时将产生大量计算消耗。

为了降低算法的计算复杂度，研究人员针对简化图卷积结构进行了大量研究。Defferrard 等人[10]采用固定的卷积滤波器来拟合卷积核，该滤波器建模K+1（K小于节点数）阶切比雪夫多项式（Chebyshev），能够极大地减少计算复杂度。由于矩阵特征分解非常依赖计算，为了解决这个问题，GCN 采用建模一阶切比雪夫多项式的滤波器，进一步降低了矩阵特征分解带来的计算消耗，时间复杂度降至O(|Ε|d)。通过该滤波器，节点能汇总来自一阶邻居的节点特征。SGC 通过移除非线性变换和压缩卷积层之间的权重矩阵，在保证良好性能的同时进一步降低了计算复杂度。以上GCNN 算法大多遵循固定策略的邻域聚合，学习到的邻域信息具有局部性，通常会影响算法的表示学习，如GCN 和SGC 都使用固定的转移概率矩阵和聚合操作。

近几年提出了一些多样化邻域聚合的算法，例如GAT（graph attention networks）[13]、GraphSAGE（graph with sample and aggregate）[14]、APPNP（approximate personalized propagation of neural predictions）[15]等。GAT 算法在GCNN 中引入注意力机制概念，来为每个节点分配不同的重要性权重，利用学习的权重来聚合节点特征。GraphSAGE 改进了GCN 的邻居采样和聚合方式。由全图的采样邻居策略改为以节点为中心的小批量节点采样，然后它又拓展了邻域的聚合操作，使用元素平均或者加和、长短期记忆（long short-term memory，LSTM）和池化（pooling）方法聚合邻域节点特征。这些方法只考虑几个传播步骤内的节点，并且所利用邻域的大小很难扩展。Klicpera 等人[15]研究了GCN 与PageRank 的关系，提出了改进传播方案和相应算法APPNP。APPNP 解耦了预测和传播过程，在不引入附加参数的情况下，通过可调的传送概率α，对保留局部信息或是利用大范围邻居信息进行平衡。上述算法展现了不错的性能，但是无法从深度模型中获益，因为增加层次会使算法出现过平滑问题，所以它们都聚焦于构建浅层模型。

为了解决过平滑问题，通过增加模型深度来挖掘更多深层次信息，一批算法被提了出来，例如JKNet（graphs with jumping knowledge networks）[16]、GCNII（graph convolutional network with initial residual and identity mapping）[17]、DeepGWC（deep graph wavelet convolutional neural network）[18]等。Xu等人[16]首先验证了嵌入节点的邻域信息范围存在差异，针对这个问题，JKNet 依次建模每个层级上的邻域聚合信息，最终通过几种聚合方式（如连接、最大池化、LSTM 等）组合了它们，实现了更好的结构感知表示。GCNII在使用初始残差连接输入的基础上，增加了恒等映射将单位矩阵添加到权重矩阵，这两种技术可以防止过平滑并提高算法性能。Chen 等人[17]从理论上证明了GCNII 能表示一个具有任意系数的K阶多项式滤波器，能够有效地聚合K阶邻域特征。DeepGWC 采用傅里叶基和小波基相结合的方法改进了图小波神经网络中静态滤波矩阵的构建方案，同时结合残差连接和恒等映射，实现了更好的深度信息聚合的目标。尽管通过聚合特征生成的嵌入表示已经很好地反映了邻域相似性，表现出良好的实践效果，但是图数据中仍存在尚未挖掘的深层次信息，获取这些邻域信息有助于提升算法在下游任务中的表现。

AIR-GCN[19]首次将邻域交互纳入建模思路中，以此获取到图中未被考虑到的非线性信息。它提供了一种邻域聚合信息和邻域交互信息的建模策略，该策略的执行过程由端到端框架进行监督，具有优异的特征学习能力。但是AIR-GCN 算法存在几个问题，会导致学习的节点嵌入表示在下游任务中表现不佳：

（1）在融合邻域聚合项和邻域交互项时，AIRGCN 借助残差学习[20]概念对这两个信息项进行跳跃连接加和，这种做法忽略了两个邻域信息项对于后续任务有不同的重要性。

（2）在AIR-GCN 学习过程中，未考虑到高熵值的预测概率可能会影响节点嵌入表示，导致局部邻域内节点特征的一致性不足。

（3）由于AIR-GCN 使用同一图数据，分别经三条图卷积通道获得三组预测概率，可能出现各图卷积通道的预测输出之间独立性不足问题，导致生成的嵌入表示之间差异性不足。

针对AIR-GCN 算法存在的问题，本文提出了自适应融合邻域聚合和邻域交互的图卷积网络（graph convolutional network with adaptive fusion of neighborhood aggregation and interaction，AFAI-GCN）。本文的主要贡献总结如下：

（1）注意力机制已经被广泛地应用在图神经网络研究中[13,21]，其核心是从众多信息中选择对当前任务目标更关键的信息。受此启发，针对问题（1），在融合模块中添加了注意力机制，它在信息融合时增加了关注标签信息的参数，能自适应地学习邻域信息项的注意力值，加权融合后得到更适合下游任务的嵌入表示。这个方案建立了深层次信息的融合方法与节点表示之间的关系（见2.3 节）。

（2）针对问题（2）和问题（3），在目标函数中引入一致性正则化损失和差异性损失。一致性正则化损失能限制图卷积通道输出低熵值的预测，提高邻域内节点的一致性，从而提升算法在节点分类任务中的表现。差异性损失对通道施加独立性限制，弥补嵌入表示之间差异性不足的问题（见3.2 节、3.3 节）。

（3）三个公开经典数据集上的实验结果表明了AFAI-GCN 算法的有效性，AFAI-GCN 框架有效提高了基准图卷积算法在节点分类任务上的性能（见第4 章）。

1 背景知识

定义1（属性图）属性图表示为G=(V,A,X)，其中V是节点集合，A∈Rn×n是邻接矩阵，Ai∈Rn×d表示节点i的链接情况，元素的取值有{0,1}，Aij=1 表示节点i与节点j之间存在连接，Aij=0 表示节点i与节点j之间不存在连接。X∈Rn×d是属性矩阵，Xi∈Rn×d表示节点i的属性，n表示图中节点总数，d表示属性维度。

定义2（残差学习）残差学习是指在神经网络的两个层之间增加捷径（shortcut），它能缓解误差反向传播中出现的梯度消失和梯度弥散问题[20]。残差网络借助跳跃连接对输入数据和它的非线性变换进行线性叠加，这个环节有助于在高阶特征的学习过程中注入低阶特征，使算法脱离局部最优值。残差学习的特征表示为h(x)，它的算式如式（1）所示：

其中，f(x)表示当前隐藏层的嵌入特征，x表示输入的特征表示。

定义3（邻域聚合）邻域聚合是节点通过汇总其局部邻域中节点的特征信息，得到自身的嵌入表示。聚合邻域特征的必要前提是邻域相似性，它是指相互连接的节点应该是相似的，即节点和其邻居节点的嵌入表示应该是相似的[22]。因此GCNN 算法利用节点之间的连接来传播特征信息，从而保证了嵌入空间中节点的相似性近似于原始网络中节点的相似性。

图1 以节点A的一次邻域聚合为例描述其流程。首先输入一个属性图，利用权重矩阵对所有节点的属性进行仿射变换，将其从原始网络空间映射到新的嵌入空间中（这个过程一般包含属性维度的降维）；然后借助图的结构信息，确定节点A的一阶邻域节点集合，这里节点A的一阶邻居节点集合为{A,B,C,D}；使用这些节点的嵌入表示进行加权求和，得到节点A关于邻域聚合的嵌入表示；根据后续任务确定是否进行非线性转换。

图1 建模邻域聚合项Fig.1 Model neighborhood aggregation terms

定义4（邻域交互）邻域交互是节点通过汇总其局部邻域中节点的相互影响，得到自身的嵌入表示。在训练过程增加邻域交互计算环节，可以帮助算法获取更多图中的非线性信息[19]。

图2 以节点A进行一次邻域交互计算为例描述其流程。首先输入一个属性图，用权重矩阵将节点的属性从原始网络空间仿射到嵌入空间；然后确定节点A的一阶邻居节点集合{A,B,C,D}，将这些节点的嵌入表示每两个一组进行元素相乘，计算邻域节点之间的相互影响，得到6 个邻域相互影响因子；使用这6 个信息项进行加权求和，得到节点A关于邻域聚合的嵌入表示；最终的嵌入表示可以根据后续任务进行非线性转换。

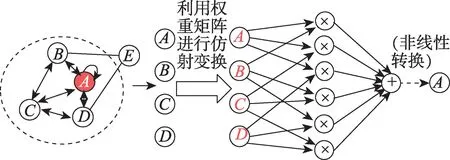
图2 建模邻域交互项Fig.2 Model neighborhood interaction terms

2 算法描述

为了实现更高效的信息融合，提高分类器的性能，保证各通道相对独立地获取信息，本文在引入邻域聚合和邻域交互概念的基础上，设计了自适应融合邻域聚合和邻域交互的图卷积网络AFAI-GCN，它的总体框架如图3 所示。图中数据输入到图卷积网络通道后，不同的颜色代表不同的向量表示。

图3 AFAI-GCN 的框架Fig.3 Framework of AFAI-GCN

算法使用属性图作为输入数据。邻域聚合模块使用双通道图卷积层，汇总邻域节点特征来生成节点嵌入表示，输出两个不同的邻域聚合项；邻域交互模块使用这两个邻域聚合项，对应位置进行元素相乘，计算邻域之间的相互作用，得到邻域交互项；选择上述两个邻域聚合项中的任意一个，和邻域交互项一起输入到自适应融合模块中；自适应融合模块中添加了注意力机制，它在算法学习过程中注入标签信息，分别计算邻域聚合项和邻域交互项的注意力权重，进行注意力权重的加权融合，得到邻域聚合与邻域交互信息的融合项；输出模块使用三通道图卷积层，进一步汇总二阶邻域中节点的特征信息，分别输出三组预测概率。

图卷积层每增加一层，节点相应地聚合更高一阶的邻域信息，但是图卷积无法像CNN（convolutional neural networks）层结构一样堆叠很深的层次。Li 等人[23]的研究表明，GCN 在进行一阶、二阶邻域的特征聚合时，学习得到的节点表示向量在后续任务中表现最好。堆叠多层图卷积反而会使节点的表示向量趋于一致，出现“过平滑（over-smooth）”现象。邻域交互项量化了两个邻域聚合项之间的相互影响，需要利用双通道图卷积层分别学习两个不同的邻域聚合项。因此在AFAI-GCN 的算法框架中，构建了两个图卷积网络通道，每个通道包含两个图卷积层。

下文详细介绍邻域聚合模块、邻域交互模块、自适应融合模块以及输出模块这四个主要环节。

2.1 邻域聚合模块

第1 章中定义3 提到，邻域聚合是指通过组合相邻节点的特征信息来生成节点的特征表示，它是图卷积层处理特征的主要环节，节点i的邻域聚合项为，它的计算过程如式（2）所示：

其中，eij是一个标量，它表示节点j的特征对于节点i的重要性；是第j个节点的嵌入表示；是参数矩阵；σ()∙是非线性的激活函数；Ni是包含节点i本身和其一阶邻居的集合。

不同的GCNN 算法在设计邻域聚合结构时，采取的策略也不尽相同，这里主要介绍三个关于邻域聚合的方法。

（1）GCN 中邻域聚合结构的设计思路是构建重要性矩阵E，使其能合理地反映节点之间的影响。首先，为每个节点增加自连接，得到新的邻接矩阵=A+I，I是单位矩阵，使得邻域概念更符合逻辑；为了防止多层网络优化时出现梯度爆炸或梯度弥散，对进行归一化处理，即，将其元素取值限制在(-1,1]范围内。GCN 在第k层中生成的邻域聚合项，它的计算过程如式（3）所示：

其中，中的元素aij是预处理后的重要性值，对应式（2）中的eij。

（2）SGC 在设计邻域聚合结构时主要考虑如何使算法变得更简单。从理论上证明了K>1 时，起低通滤波器的作用。因此它移除了邻域聚合结构中的非线性激活函数，仅靠线性堆叠K层的归一化邻接矩阵和一层的权重矩阵来平滑图的表示。任意取k≤K，SGC 在第k层中生成邻域聚合项的过程如式（4）所示：

（3）GraphSAGE 在设计邻域聚合结构时，主要考虑扩展固定的邻域聚合策略。它为每个节点学习一组聚合函数，以此灵活地聚合邻居节点特征；它提出了三种聚合函数的选择：元素平均或加和、LSTM 和池化。聚合函数为最大池化的邻域聚合项，它的计算过程如式（5）所示：

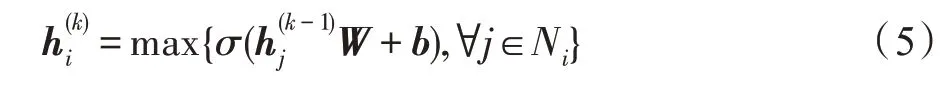
其中，max{∙}是最大值函数。

本文算法中，邻域聚合模块使用属性图G=(V,A,X)作为输入，通过双通道图卷积层输出两项不同的邻域聚合嵌入表示。节点i经邻域聚合模块生成两个邻域聚合项，计算过程如式（6）所示：

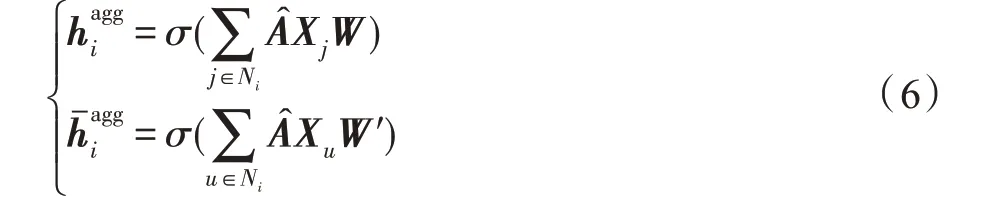
其中，σ选择ReLU(x)=max(0,x)函数。

选择GCN 层结构作为本文算法中邻域聚合模块的网络结构，构建了一个适用性较强的图卷积网络框架。大多数GCN 层结构的改进算法均可与本文提出的框架兼容。

2.2 邻域交互模块

第1 章中定义4 提到，邻域交互是指通过组合局部邻域中节点的相互影响来生成节点的特征表示。建模邻域的相互影响，能够使算法获取到部分图中深层次的非线性信息。

其中，σ选择Sigmoid 函数。βju是一个标量，表示节点j的邻域聚合项与节点u的邻域聚合项之间的交互权重，其值越大表示节点j和t的互相影响中包含越多节点i的相关信息。

计算两次邻域聚合之间的相互影响时可以选择的向量运算有：逐元素加、减、乘、除，逐元素取平均值、最大值、最小值等。本文采用逐元素乘法，这个运算能满足计算邻域之间相互作用的实际需求。

2.3 自适应融合模块

为了利用残差学习产生的性能优势，AIR-GCN在信息融合时基于邻域聚合项和邻域交互项进行跳跃连接加和。这种做法忽略了两个信息项对于任务重要程度的差异，融合后的嵌入表示可能在后续任务中性能不佳。针对上述缺陷，AFAI-GCN 在融合模块中增加了注意力机制，它在融合过程中注入标签信息，学习关于上述两个信息项的注意力值，使用学习的注意力值进行加权求和，得到融合邻域聚合和邻域交互信息的嵌入表示。

2.4 输出模块

3 目标函数

目标函数是指算法训练过程时需要优化的损失函数集合。在设计半监督的GCNN 算法时，目标函数除了包含带标签节点的监督损失，通常还会组合图正则化损失，通过正则化损失来平滑图上的标签信息[11,24]。本文算法在目标函数部分主要进行了以下两项改进：

（1）高熵值的预测概率可能会导致局部邻域内节点特征的一致性不足。因此在目标函数中添加信息一致性约束，它有助于增强局部邻域内节点特征的一致性，提升算法在节点分类任务中的表现。

（2）多个通道使用同一图数据并且它们并行工作，需要考虑通道的预测输出之间的相互影响。因此在目标函数中添加了信息差异性约束，它能对各个通道的预测输出施加独立性限制，使算法获取更多样的深层次信息。

综上所述，本文在保留监督损失的基础上，在目标函数中添加了两个信息约束项，目标函数包括监督损失、一致性正则化损失和差异性损失三项，下面对它们进行详细说明。

3.1 监督损失

其中，z∈Rn×C是分类器的预测概率，y∈Rn×C是真实数据标签，C表示类别总数。

3.2 一致性正则化损失

为了优化算法在分类任务中的表现，应该避免分类器的决策边界穿过数据边缘分布的高密度区域[25]。为了实现这个目标，一种常见的做法是限制分类器输出未标记数据低熵的预测[26]。遵循这个思路，本文在目标函数中添加了信息一致性约束，它能限制算法的预测输出，使其概率分布的平均方差更小，图的嵌入表示更加平滑。

AFAI-GCN 中使用了三个图卷积通道，为此需要拓展上述思路来适应多通道结构。首先使用式（13）计算所有预测概率的平均值，得到预测概率的中心。

如果标签分布的熵值较高，则意味着学习到的节点与其邻居特征或标签的差异性较大，这不利于表达邻域相似性，进一步聚合可能会损害算法性能[22]。因此获取到平均预测zˉ后，利用Sharpen[26]技巧来减少标签分布的熵。表示节点i在第j类上的低熵的预测概率，它的计算过程如等式（14）所示：

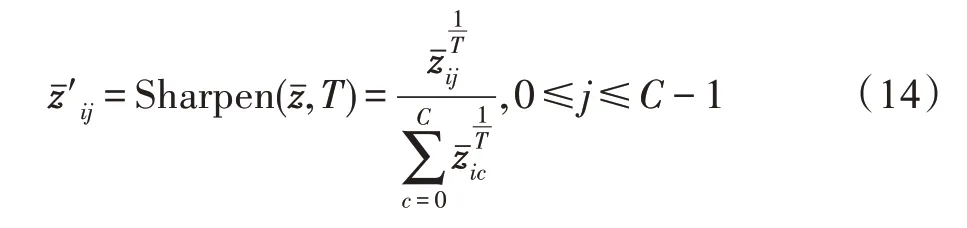
其中，T是一个参数，当T→0 时，Sharpen(,T)的输出将接近Dirac 分布，此时概率分布中所有的值都集中在一点附近，因此使用较低的T值会使算法输出较低熵的预测。

使用Lc表示一致性正则化损失，它表示与多个输出预测z的平方L2范数，计算过程如式（15）所示：

3.3 差异性损失

本文在目标函数中添加了信息差异性约束，它能度量随机变量之间的独立性，有利于量化分析通道之间的相互影响。差异性约束采用一种基于核的独立性度量——希尔伯特-施密特独立性准则（Hilbert-Schmidt independence criterion，HSIC）。

这类方法的总体思路是，利用再生核希尔伯特空间上定义的互协方差算子推导出适合度量独立性的统计量来决定独立性的大小[27]。

假设X、Y是两组可观测变量，对于x∈X和y∈Y分别定义其再生核希尔伯特空间B、Q上的映射Φ(x)∈B和Ψ(y)∈Q，得到对应的核函数为k(x,x′)和l(y,y′)，它们的计算过程如式（16）所示。

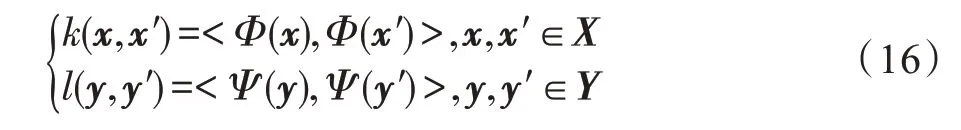
互协方差算子可以表示为Cxy:B→Q：

其中，⊗表示张量积，ExΦ(x) 和EyΨ(y) 分别表示Φ(x)和Ψ(y)的期望。

HSIC 通过计算Hilbert-Schmidt 互协方差算子范数的经验估计值得到独立性判断准则，它的表达式如式（18）所示。

当得到观测数据{(x1,y1),(x2,y2),…,(xn,yn)} 时，HSIC 的经验估计值如式（19）所示：

其中，R=I-(1/n)eeT，I表示单位矩阵，e是元素值为1 的列向量，K和L分别是核k和l关于观测值的Gram 矩阵[28]，即Kij=k(xi,xj)，Lij=l(yi,yj)。

经输出模块获取三组预测概率zagg、zaair和。由于它们是从同一个图G=(V,A,X)中学习的，需要增加一个信息约束项来确保它们可以获取到不同的信息。为此在目标函数中增加差异性损失Ld，它是zagg、分别与zaair计算的HSIC 值之和，计算过程如式（20）所示：

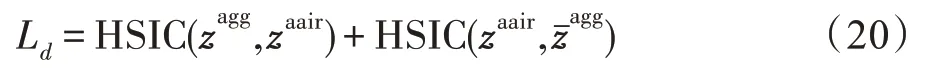
核函数相当于两个样本之间的相似度，本文算法的实现中选择内积核函数来描述这种关系，即K=z∙zT。

HSIC 的经验估计值在理论上已经被证明，其值越大说明两个变量关联性越强，越接近0 说明两个变量独立性越强[29]。引入这项约束可以辅助优化算法，在训练过程中对其进行最小化，能提高两对预测概率之间的独立性，有助于图卷积通道学习本身的特有信息，从而提高两组嵌入表示的差异性。

3.4 优化目标

算法需要优化的总体目标函数是上述三种损失的加权和形式，计算过程如式（21）所示：

其中，κs是第s个图卷积通道上监督损失的权重，t和r分别为一致性正则化损失的权重和差异性损失的权重。算法利用带标签的训练样本进行数据学习，反向传播时最小化目标函数来进行模型优化。

根据第3 章对AFAI-GCN 中主要模块及目标函数的详细介绍，算法1 给出了具体的算法流程。

算法1AFAI-GCN 算法

4 复杂度分析

本章首先分析算法各模块的时间消耗，得出总体时间复杂度，然后调用torchsummary 工具对模型占用的缓存大小进行估计，计算其空间消耗。假定n是总节点数，m是总边数，d是属性维度，di表示第i个图卷积层输出的特征维度，d′表示注意力层的维度。

对于GCN 算法，计算的时间复杂度为O(md1+ndd1+md2+nd1d2)。ndd1、nd1d2涉及特征表示与参数矩阵的乘法环节，md1、md2表示邻域聚合过程的时间消耗。在Cora、Citeseer、Pubmed 数据集上的参数总量分别为0.09 MB、0.23 MB、0.03 MB。AIR-GCN的时间复杂度为O(md1+ndd1+md2+nd1d2+nd1)，它在计算邻域交互项时增加了元素乘法和加法环节，所产生的时间代价大约为O(nd1)。AIR-GCN 采用双通道图卷积结构，因此其空间消耗大约是GCN 算法的两倍，在Cora、Citeseer、Pubmed 数据集上的参数总量分别为0.18 MB、0.45 MB、0.06 MB。AFAI-GCN的总体时间复杂度为O(md1+ndd1+md2+nd1d2+nd1+nd1d′)。相较基准算法AIR-GCN，AFAI-GCN 在融合模块中添加了注意层来为融合过程注入标签信息，该环节的时间消耗大约为O(nd1d′)。由于通常限制d′比d1更小以得到稠密的注意力值中间向量，AFAIGCN与AIR-GCN具有相似的计算时间成本。在Cora、Citeseer、Pubmed数据集上的参数总量分别为0.18 MB、0.45 MB、0.06 MB，因此AFAI-GCN 与AIR-GCN 有相似的空间消耗。详细内容如表1 所示。

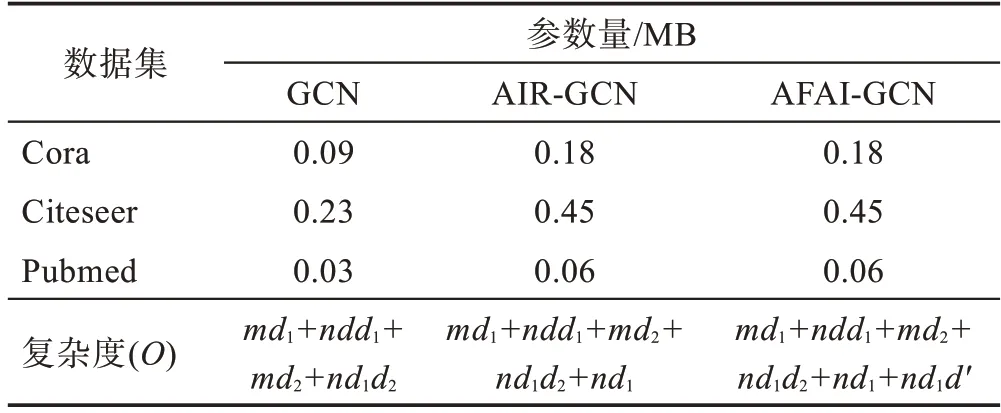
表1 算法参数量及复杂度Table 1 Algorithm parameters and complexity

5 实验

5.1 实验设置

本节主要介绍数据集及样本选择、基准方法和参数设置。

5.1.1 数据集及样本选择

所有实验在3 个公用引文数据集Cora（机器学习引文网络）、Citeseer（会议引文网络）和Pubmed（生物医学引文网络）上进行。

样本选择时采用统一方案，每类随机选择20 个带标签的节点组成训练集，500 个节点组成验证集，1 000 个节点组成测试集。表2 展示了3 个数据集的详细信息以及样本选择情况。

表2 数据集及样本选择Table 2 Datasets and sample selection

5.1.2 基准方法

在节点分类实验中，将AFAI-GCN 算法与数种图表示学习经典的算法进行比较，这些方法包含两个神经网络模型MLP（multilayer perceptron）[30]、LP（label propagation）[31]，两个网络嵌入算法DeepWalk、Planetoid 和6 个近期研究热度较高的GCNN 算法GraphSAGE、Chebyshev、GCN、SGC、GAT、AIR-GCN。

5.1.3 参数设置

为了保证实验的公平性，基准算法均选择其论文中的默认参数。在重复参数进行初始化时，AFAIGCN 与基准算法GCN、AIR-GCN 保持相同参数值。设计模型结构时，设定图卷积层数为2，中间层维度为16，每一层的Dropout 率为0.5。算法优化器选择学习率为0.01 的Adam 优化器，权重衰减率为5×10-4。参考文献[26]，一致性正则化约束中的超参数T设置为0.5，5.7 节中分析注意力层的维数和两个新增损失函数的权重对算法性能的影响。

5.2 节点分类结果

节点分类任务是现阶段图表示学习方法评估中常用的下游任务。表3 展示在相同实验条件下每个算法随机运行10 次的平均值，结果使用准确率（Accuracy）作为评价指标。其中加粗的数值为最优结果，带下划线的数值为次优结果。

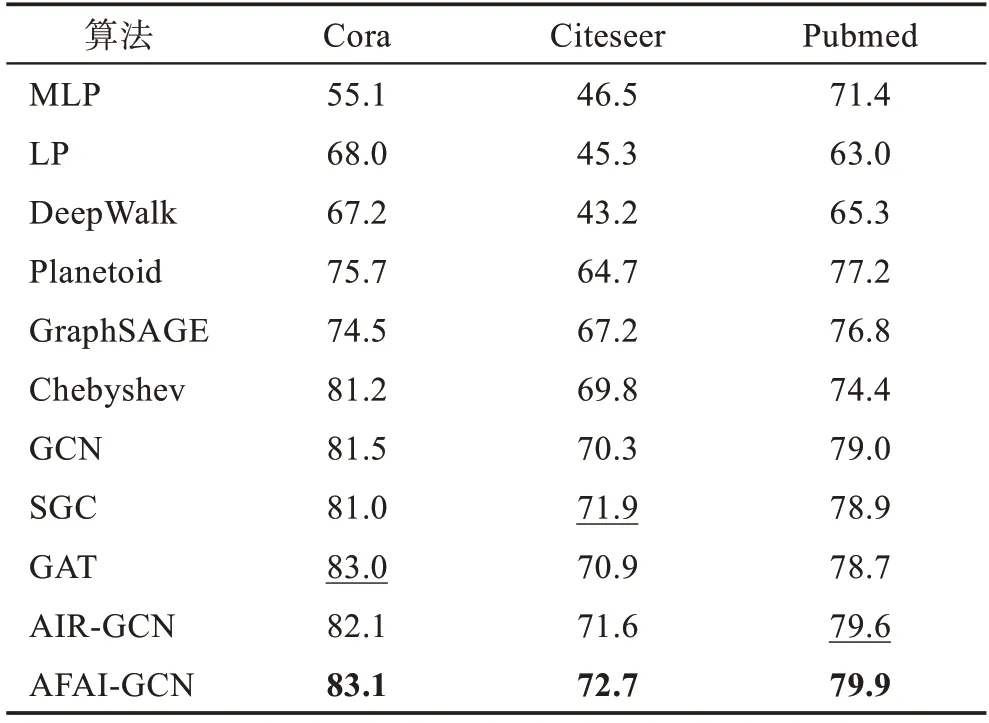
表3 节点分类的Accuracy 指标结果Table 3 Accuracy performance of node classification 单位：%

从表3 中可以观察出：在实验条件相同情况下，与所有基准算法相比，AFAI-GCN 算法节点分类的平均准确率最高。在三个公用数据集Cora、Citeseer、Pubmed 上，AFAI-GCN 的平均准确率比基准算法GCN 的平均准确率分别提高了1.6 个百分点、2.4 个百分点、0.9 个百分点，比AIR-GCN 的平均准确率分别提高了1.0 个百分点、1.1 个百分点、0.3 个百分点。以上结果验证了AFAI-GCN 算法的有效性。

结果分析如下，相较于GCN、SGC 等图卷积网络算法仅通过建模邻域聚合信息来进行算法学习，AIR-GCN 在建模时增加邻域交互项来促使算法学习其他的非线性信息，补充了嵌入表示所包含的信息。AFAI-GCN 在AIR-GCN 基础上，利用注意力机制在信息融合时增加了对重要信息项的关注，得到注意力值的加权融合项。这个环节能更充分地利用节点标签信息，为算法提供额外的弱监督信息，更好地关注信息融合趋势。在节点分类任务中，这些弱监督信息会帮助算法学习到更适合下游任务的嵌入表示，因此AFAI-GCN 的分类性能优于AIR-GCN。一致性正则化损失和差异性损失对算法学习的嵌入表示进行信息约束，分别提高了节点特征一致性和嵌入表示之间的差异性，使算法的分类效果优于上述基准算法。

5.3 可视化

为了直观地比较算法分类性能，本节进行节点的嵌入表示的可视化处理。实验利用t-SNE[32]工具，将算法学习到的嵌入表示投影到二维空间中，以便直接观察原始网络的群落结构。图4 展示了GCN、SGC、AIR-GCN、AFAI-GCN 算法在Citeseer数据集上的可视化结果。图中每个点都代表真实网络中的一个节点，不同的颜色代表不同的节点类别，图例中有6 个类别标记{C0,C1,C2,C3,C4,C5}。

图4 Citeseer数据集的可视化结果Fig.4 Visualization of Citeseer dataset

从图4 可以观察到：对于Citeseer 数据集，GCN可视化的节点分布较为混乱，存在混合较多不同颜色的节点簇，SGC、AIR-GCN 和AFAI-GCN 的可视化节点分布更合理，节点簇中颜色更统一。比较SGC、AIR-GCN 和AFAI-GCN，能看出AFAI-GCN 的可视化效果最好，簇内节点的聚合程度更高，不同的团簇之间边界更清晰。例如：（d）图中C1、C2 的团簇结构比（b）图和（c）图中对应结构更紧簇。结合图4 的可视化结果和表3 的平均准确率结果可知：节点分类任务中，AFAI-GCN 的性能优于其他基准算法的性能。

仅通过可视化图像展示和节点分类结果的数值呈现，不能得出各改进部分对算法性能的实际影响。5.4 节、5.5 节将深入讨论注意力机制的实际意义和两个信息约束项的作用。

5.4 变体算法分析

本节考虑到一致性正则化损失和差异性损失的不同组合，提出3 个AFAI-GCN 的变体算法，进行消融实验，证明添加一致性正则化损失和差异性损失的有效性。在3 个数据集上分别运行这4 个算法，报告10 次随机运行的平均准确率。实验结果如图5 所示，图例中四个简称分别代表的含义是：AFAI-GCNo 表示无Lc和Ld约束的AFAI-GCN，AFAI-GCN-d 表示仅使用差异性约束Ld的AFAI-GCN，AFAI-GCN-c表示仅使用一致性正则化约束Lc的AFAI-GCN，AFAI-GCN 表示同时使用一致性正则化约束Lc和差异性约束Ld的完全体AFAI-GCN。

图5 AFAI-GCN 及变体的节点分类结果Fig.5 Node classification results of AFAI-GCN and variants

观察图5 可以得出以下结论：（1）在3 个数据集上，添加一致性正则化约束Lc和差异性约束Ld的完全体AFAI-GCN 的准确率均优于其他三个变体算法，这表明了同时使用这两种约束会提升算法的分类性能。（2）AFAI-GCN-d、AFAI-GCN-c 和AFAI-GCN 在所有数据集上的分类结果均优于AFAI-GCN-o，表明了单独使用或同时使用两个约束均会提升算法的分类性能，结果验证了这两个约束的有效性。（3）比较图5 和表3 的结果可以看出，与基准算法AIR-GCN 对比，只有监督损失项的AFAI-GCN-o 仍然有更好的分类表现。这表明在融合模块中添加注意力机制对算法的性能产生了正面的影响，本文提出的基础框架稳定并且性能更优。

5.5 注意力机制分析

为了考察在融合模块中添加注意力机制的实际效果，本节详细分析注意力层的学习细节。分别在3个数据集上，绘制注意力层生成的注意力平均值的变化趋势，并标记出最大值、最小值，结果如图6 所示。x轴是迭代次数，y轴是注意力平均值。图例中，HirAtt、HaggAtt、MinAtt、MaxAtt 分别表示邻域交互项的注意力值、邻域聚合项的注意力值、最小注意力值和最大注意力值。

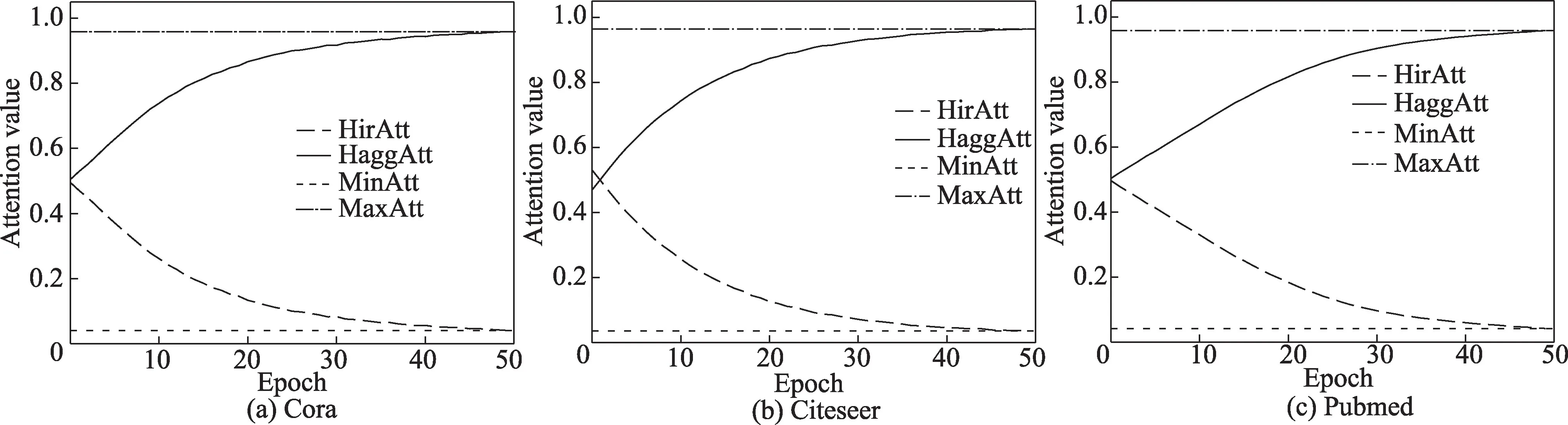
图6 注意力值的变化Fig.6 Change of attention value

实验结果显示：训练开始时，邻域聚合项和邻域交互项的平均注意力值在0.5 附近，训练过程中它们发生了明显的变化。例如在Citeseer 数据集上，邻域交互项的平均注意力值的初始值为0.5，随着算法迭代，该值逐渐减少，最终收敛值接近0。邻域聚合项的平均注意力值则随着训练进行不断增加，该值在30 次迭代后超过0.9。

实验结果说明，自适应融合模块中的注意力层能够逐步学习到不同嵌入表示的重要性。配合图5中AFAI-GCN-o 的准确率结果，能够得出AFAI-GCN算法学习时注意力机制的有效性。

5.6 收敛性分析

本节实验对比AFAI-GCN 和基准算法AIR-GCN的收敛性，在3 个数据集上分别绘制两个算法训练过程中测试准确率曲线。结果如图7 所示。

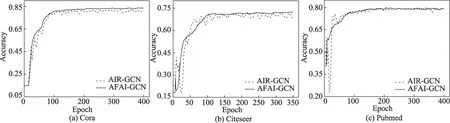
图7 收敛结果Fig.7 Convergence results

结果表明：在3 个数据集上，AFAI-GCN 的收敛速度普遍比基准模型AIR-GCN 要快，训练过程的准确率分布更稳定。因此AFAI-GCN 算法展现出了更快的收敛速度和更高的收敛稳定性。

5.7 参数敏感性分析

本节通过实验分析注意力层的维数p、一致性正则化损失权重t和差异性损失权重r对算法节点分类性能的影响。每次确定一个分析参数，固定两个非分析参数，改变分析参数的数值来研究它对算法的影响。

注意力层维数p是一个可以调节模型结构的超参数。考虑到算法的计算复杂度，注意力层维数p取区间[1,15]中的15 个整数值。保持其他参数不变，在3 个数据集上分别运行10 次算法，报告它们的平均准确率值，结果如图8 所示。

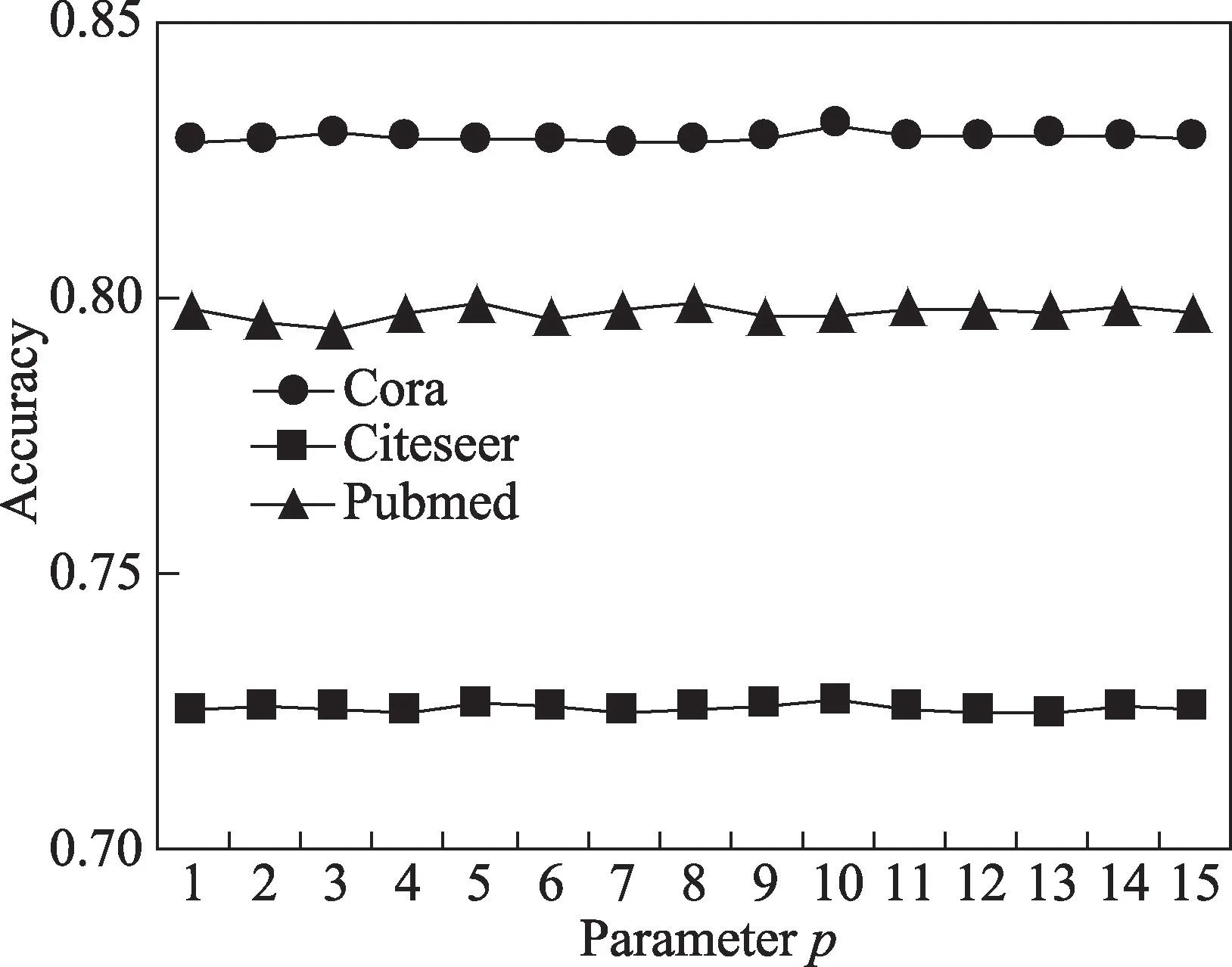
图8 参数p 的影响Fig.8 Influence of parameter p

实验结果显示：（1）三条折线的波动幅度较小，说明在上述取值区间内，p值对性能指标准确率的影响不大，说明本文算法对参数p的敏感性低。（2）在Cora、Citeseer、Pubmed 数据集上，注意力层的维数p分别取10、8、10 时，算法的分类准确率最高。（3）结合图8 和表3 的实验结果，即使在分类性能最差的情况下，AFAI-GCN 对比其他基准算法表现仍然更好。

图9 展示一致性正则化损失权重t对算法节点分类性能的影响，实验中将其取值从1.0E-04 调整到1.0E+00。可以观察到：在3 个数据集上，随着权重t的增加，算法的分类性能均缓慢提高。t在1.0E-04 至1.0E+00 范围内时，AFAI-GCN 的分类表现都是稳定的，说明AFAI-GCN 对参数t的敏感性较低。在3 个数据集上，一致性正则化损失权重t取值为1.0E+00时，算法分类准确率最高。

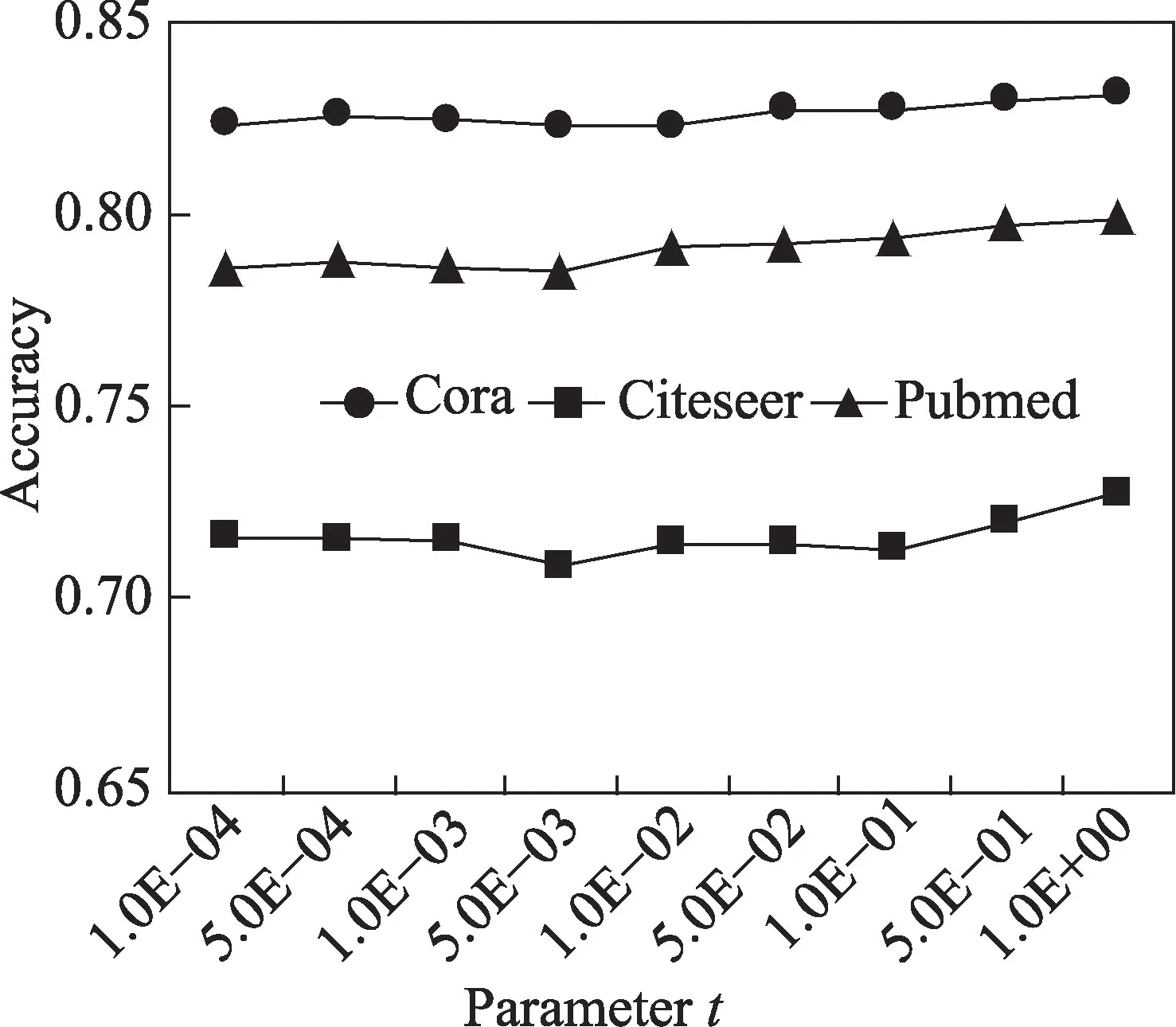
图9 参数t的影响Fig.9 Influence of parameter t

图10展示差异性损失权重r对算法节点分类性能的影响，实验中将其取值从1.0E-05 调整到1.0E-01。在图10中可以观察到：在3个数据集上，r在1.0E-05至1.0E-01 范围内时，AFAI-GCN 的准确率呈现不稳定状态，说明算法对参数r的敏感性较高。在3 个数据集上，差异性损失权重r取值为1.0E-04 时，算法分类准确率最高。

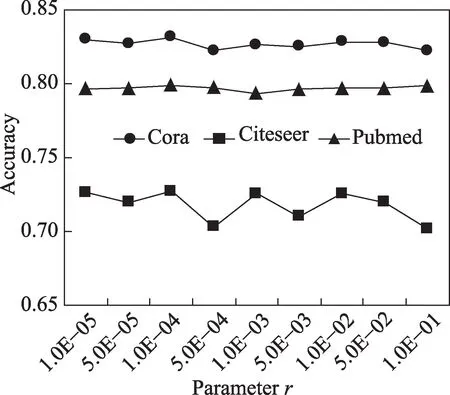
图10 参数r的影响Fig.10 Influence of parameter r

6 结束语

在图表示学习方法研究的基础上，利用图卷积神经网络学习图的嵌入表示，其结果在下游任务中表现出优异的性能。本文在引入邻域聚合和邻域交互概念的基础上，提出了自适应融合邻域聚合和邻域交互的图卷积网络AFAI-GCN，探索了深层次信息的融合逻辑与节点表征之间的关系。AFAI-GCN 在融合模块中添加了注意力结构，它能针对下游任务自适应地学习融合权重，以合适的比例融合上述两种信息，这是一种有效可行的GCNN 信息提取机制；同时算法中添加了一致性正则化约束和差异性约束两项信息限制，分别提高了邻域内节点特征的一致性和嵌入表示之间的差异性，使得AFAI-GCN 在下游任务上的性能超越了基准图神经网络模型的性能。未来的研究包括提升模型效率使其适用于更大规模的网络，扩展深度使其获取到更多深度信息。