多语义关系嵌入的知识图谱补全方法

尹 华，肖石冉，陈智全，胡振生，龙泳潮

1.广东财经大学 信息学院，广州510320

2.广东省智能商务工程技术研究中心，广州510320

3.中山大学 计算机科学与工程学院，广州510006

知识图谱作为一种大规模语义网络，是图书情报领域的关键前沿技术，已成功运用于信息检索[1]、推荐系统[2]、问答系统[3]等，其构建的基础是实体（概念）及关系抽取，即三元组(h,r,t)（头实体、关系、尾实体）抽取。由于关系抽取高度依赖于实体抽取，实体及关系抽取的不完备性导致知识图谱的关系缺失问题[4-5]。知识推理是利用已知的知识推理出新知识的过程。通过面向知识图谱的知识推理，即知识图谱推理，在已抽取的三元组集合中，推理获得三元组中的缺失关系，可以构建更为完备的知识图谱。

知识图谱推理的方法分为基于规则的[6]、基于分布式表示的[7]、基于神经网络的[8]、混合模型[9]等。基于规则的推理可解释性强，但规则不易获得，可计算性较差。基于神经网络的推理能力较强，但复杂度高，可解释性弱。混合推理方法目前缺乏较深层次的混合模式。而基于分布式表示的推理利用知识表示模型，得到知识图谱的低维向量表示，通过向量操作进行推理预测，计算方便快捷，此类方法可以简单便利地应用于知识图谱推理与补全。基于向量的知识表示模型按照表示空间的不同分为翻译模型[7]、旋转模型[10]、双线性模型[11]、神经网络模型[12]、双曲几何模型[13-14]等。在处理复杂关系问题上，大部分模型关注一对多、多对多的复杂关系，但无法覆盖所有的关系类型。旋转模型中的RotatE[10]将实体和关系映射到复数向量空间，可以同时处理上述关系。但由于其将一种关系表示为单一向量，未深入考虑关系的多语义现象。

关系多语义[15]是指同一个关系在不同的头尾实体对下会表现出不同的含义。例如吉姆·贝鲁什（Jim Belushi）既是演员又是音乐家，他同时获得了音乐奖项和影视奖项提名。对于获奖提名关系，存在两个具有相同头实体和不同尾实体的三元组（吉姆·贝鲁什，获奖提名，最佳男表演奖），（吉姆·贝鲁什，获奖提名，最受欢迎男歌手），体现了两种不同的语义。但是，根据现有基于知识表示的知识图谱补全算法，通过头实体和关系计算递推出尾实体的向量表示发现，上述两个三元组的尾实体在向量空间中体现为同一向量。显然，这样的实体与关系表示会导致预测错误。因此，用一个关系向量表示一种关系，在面对复杂关系场景下不能处理多语义情况。

为充分挖掘潜在的三元组语义关系，本文提出了一种新的知识图谱关系补全方法，该方法在基于向量的表示模型基础上，构建细粒度的关系语义分量，扩充了关系语义表达，通过语义分量簇实现多语义关系嵌入，并自适应选择最贴合实体对的关系向量，保证向量计算的唯一性。同时，在公开数据集上通过链接预测和三元组分类任务，验证该方法能处理对称关系、逆关系、组合关系等复杂关系，提升了知识图谱关系补全的效果。

1 相关工作

知识图谱补全方法可分为知识表示[16]、路径查找[17]、强化学习[18]、推理规则[19]、元学习[20]等，其中基于知识表示的补全方法将三元组映射到向量空间中，使知识图谱具有可计算性，是在已知实体中发现潜在关系的一种较为直观的方法，便于理解与运用。根据采用的知识表示模型可分为双线性模型、神经网络模型、双曲几何模型、翻译模型和旋转模型等，知识表示模型的表示能力决定了关系补全的效果。

1.1 双线性模型

双线性模型将实体定义为向量，关系定义为矩阵。基于矩阵运算使得实体和关系能够进行深层次交互，例如RESCAL[11]将关系表示为满秩矩阵，但随着关系维度的增加，复杂度会很高，难以扩展至大规模知识图谱。为此DisMult[21]提出放松关系矩阵的约束，利用对角矩阵替换关系矩阵，降低了模型过拟合的风险，但也使得该模型只能处理知识库中的对称关系，不能很好处理其他关系，也不适用于大规模知识图谱。

1.2 神经网络和双曲几何模型

以ConvE[12]、CapsE[22]为代表的神经网络模型，利用卷积层和全连接层获取交互信息，但模型缺乏解释性。双曲几何模型利用双曲几何性质建模实体的层次性。例如，以庞加莱圆盘为基础的Poincare模型[14]可以很好地处理知识图谱中实体的层次性，但由于庞加莱圆盘并不能进行复杂操作，对不同关系性质表示有所欠缺。

1.3 翻译模型

翻译模型中的TransE[7]受word2vec 的启发，利用空间向量的平移不变性，建立了头实体和尾实体之间的转换关系用于推理。计算的简易性使得TransE可以高效地处理一对一关系的知识图谱补全，但并不能处理好一对多、多对一、多对多等问题。由此，在TransE 的基础上提出了建立超平面的TransH[23]。TransH、TransE 的实体和关系都表示在相同空间中，这种表示方法无法区分两个语义近似的实体在某些特定方面的不同。为此，TransR[24]提出为每个关系构造相应的向量空间，将实体和关系在不同的向量空间中分类表示。实体的映射关系仅由关系决定，但显然头尾实体本身对映射也有影响。随后，TransD[25]提出映射函数应该与实体、关系同时相关。上述模型均不能同时解决对称关系、反对称关系、互逆关系、组合关系等问题。

1.4 旋转模型

旋转模型中的RotatE 将三元组实例视为头实体经过关系角度的旋转变为尾实体的过程描述，可以同时处理对称关系、反对称关系、互逆关系、组合关系等问题。但是，RotatE 将关系看作一个特定的向量，并没有考虑解决关系的多语义问题。

关系向量细分能够丰富语义表达。TransR 的变体CTransR 通过计算偏移量(t-h)对关系进行细分，利用AP 聚类获取簇中心，并学习一个关系转移矩阵Mr来对头尾实体进行转化，该方法的时间复杂度为O(N3×O(TransR))，不适用于大规模知识图谱补全。TransG[26]提出利用贝叶斯非参数混合模型得到关系的多个表示，通过指数函数扩大主要语义分量的影响，相较于CTransR 模型参数减少，但模型相对复杂。由于嵌入表示的差异以及模型复杂度过高，上述关系细分方法均无法解决RotatE的关系多语义问题。

2 多语义关系嵌入的补全方法

知识图谱补全的核心在于复杂关系推理，选择能够处理复杂关系的知识表示模型是确保补全效果的基础。基于RotatE 的关系补全模型能够处理复杂关系，但存在关系多语义问题。为解决这一问题，尝试了以下探索：（1）RotatE 表示模型是否存在关系多语义现象？（2）如何细分关系语义表示？（3）如何确保向量计算唯一性？（4）扩充语义表达后是否具有处理复杂关系的能力？（5）如何验证知识图谱补全效果？

2.1 RotatE 模型

RotatE 模型的假设空间源于Complex 的复向量空间，受欧拉恒等式eiπ=cosx+i sinx的启发，将实体与关系表示分离。将关系看作头实体h到尾实体t的旋转过程即t=h°r，关系向量r表示为r=是头尾实体之间的角度值，RotatE将其初始化为正态分布向量，得分函数定义为：

RotateE 能够同时推断对称、反对称、逆关系和组合关系。具体关系类型定义如下：

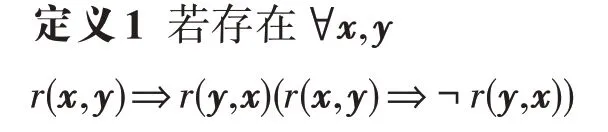
则定义关系r为对称（反对称）关系。

则定义关系r1为关系r2的逆关系。

则关系r1定义为关系r2、r3的组合关系。

尽管RotatE 能处理现有的复杂关系，但将一个关系看作一个特定的向量，其语义表达并不充分，使用RotatE 等旋转模型进行知识表示的过程中易出现部分语义表示的缺失。

在FB15K-237 数据集[27]上对RotatE 训练后获得实体集E和关系集R。利用式（2）计算得到实体集对应的关系向量，经过PCA 降维将特征向量压缩为二维向量（feature1，feature2），构造position、award_winner、nationality、sports_team_roster 四种关系角度向量可视化图，如图1 所示。

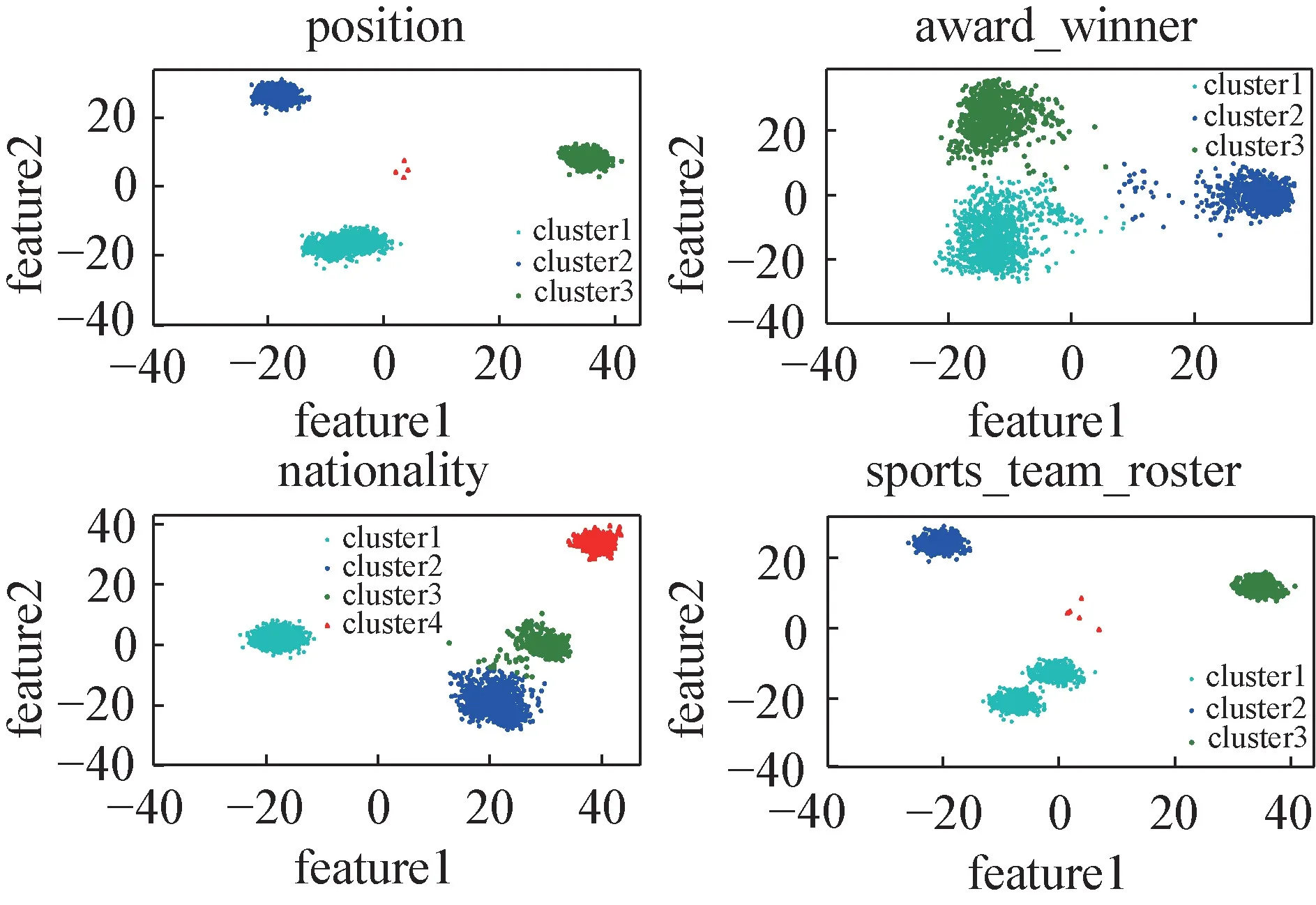
图1 基于RotateE 表示的关系角度向量可视化图Fig.1 Relation angle vector visualization based on RotatE representation

假设RotatE 将关系看作一个特定的向量是合理的。那么通过RotatE 训练后所获得的实体和关系向量表示应该是唯一的，即头尾实体之间的向量r是唯一的。经过RotatE 训练后获得的同一关系下的实体对之间的角度应当相差不大，表现在图上应为一个簇，其中心即为关系向量r的值。

分析图1 中的四种关系发现，同一关系呈现出多个簇的聚集现象，也即同一关系具有多个向量表示，与原有假设向量唯一矛盾。RotatE 中通过式（1）构建的向量空间可以看作对多个聚类簇的平均，但由于语义簇之间的差异较大，导致在关系预测中对大部分语义出现误分类的情况。由此可知，RotatE 将关系表示为单一向量并不能充分表达关系的语义信息。

2.2 MSRE 方法

为了扩充原有的关系语义表达，采用关系语义分量簇替换关系向量表达，提出一种多语义关系嵌入的知识图谱补全方法MSRE，通过关系语义细分，更多层次、多维度地发现关系。

MSRE（multi-semantic relation embedding）方 法分为三个步骤，如图2 所示。（1）计算关系语义分量。首先将知识图谱的三元组表示为实体和关系向量，再将该关系向量转化为关系角度向量集合。（2）获取关系语义分量簇。利用Mean-Shift 聚类算法自动获得关系角度向量簇。（3）关系补全。选定其中与实体对最合适的关系向量。

图2 MSRE 方法流程Fig.2 MSRE method

2.2.1 计算关系语义分量

RotatE 将关系向量定义为头尾实体之间的旋转角度，与TransE 的嵌入方法有差异，采用CTransR 在TransE 的基础上，通过r=t-h获得关系向量集合的方法并不适用。提出使用经过RotatE 训练后的实体向量，利用辅角差即式（2），得到每一种关系ri的角度向量集合即，其中ri∈R，c表示角度集合中的分量数。

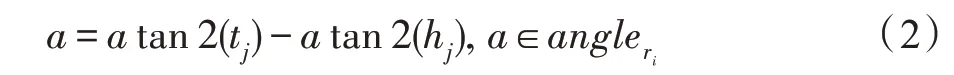
式中，tj、hj分别表示同一关系下ri的第j对头尾实体对，a的取值范围为(-π,π)。

2.2.2 获取关系语义分量簇

关系语义分量簇是指同一关系下的多种语义分量的集合clusterangleri={sub1,sub2,…,subk}，其中k表示语义分量的数量。由于每一关系下的关系语义分量较为离散，数量众多，使用聚类算法提取关系语义分量中的主要语义分量。对比多种聚类方法发现，传统K-means 算法需要手动设置聚类簇，DBSCAN（density-based spatial clustering of applications with noise）聚类方法对样本集密度不均匀，聚类间距差相差很大时，聚类质量较差[28]，基于密度的Mean-Shift[29]（均值漂移）聚类算法在高维向量空间中的聚类体现较好的效果，广泛使用在图像分割、聚类、文本分类等方面。因此，本文选择Mean-Shift算法获得语义分量簇。

为了减少无效特征的影响，本文在Mean-Shift 之前进行了PCA（principal component analysis）降维，并对聚类得到的关系语义簇进行平均化。本质上平均化的过程可以看作为关系引入全局信息，帮助模型更好地收敛。

sg表示一个半径为g的高维球区域。

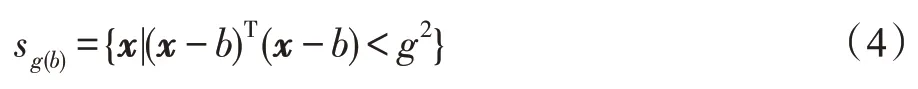
T 表示转置,xi表示为sg(b)中的一个关系角度向量，m表示关系角度向量落在sg(b)区域中的数量，Mg(b)表示下一关系角度向量的位置。经过迭代，直到收敛。得到新的关系语义分量簇，k表示关系ri中的分量数。将同一语义簇的语义关系平均化即：

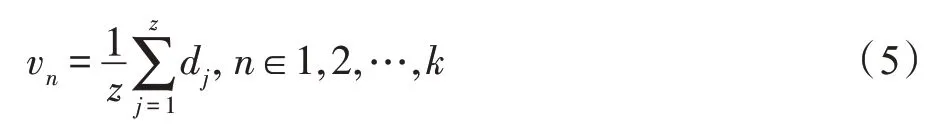
z表示rij同一簇中的关系向量数。dj是关系语义分量簇中的任意一个向量中的一个语义分量。对关系语义分量簇中的所有类经过式（5）计算后，即=(v1,v2,…,vk)，得到关系向量集合R=

2.2.3 关系补全

基于表示学习的补全模型首先在低维向量空间中对知识图谱中的实体和关系进行表示，其形式包括向量、矩阵或张量形式。然后在每个知识条目上定义一个基于三元组的打分函数，用之前给定的知识图谱表现形式判断三元组或者事实成立的可能性,即训练知识图谱中的实体集E，关系集R与关系的阈值，以判断当前三元组是否成立。

MSRE 方法中，以知识图谱中的实体向量作为输入，对每一种关系都用一个语义分量簇进行表示，即关系向量集合R，随机构造不属于三元组集的负例进行训练。训练后，对于一个待判断的实体对，不同的关系以及不同关系的不同语义分量，根据式（6）获得不同得分。分数越高表明该实体对越有可能满足这一关系。

其中，k表示聚类后得到的分类数。

为使引入关系分量簇的过程不降低模型的准确性，本文定义关系的选择策略为最符合实体对的关系向量,即得分函数最高的关系分量作为三元组中的关系分量。

结合Pytorch 中提供的计算图机制能够在扩大关系簇分量的基础上不降低模型的准确度。负例三元组的生成策略和损失函数的定义与原RotatE 模型相一致，得到每个关系分量自适应的关系向量表示，采用Adam 优化器对模型进行训练。并在模型效果相对稳定时设置学习率衰减策略即折半衰减以防止过拟合等问题的发生。具体算法描述如下：

算法1MSRE 算法

MSRE 算法的时间复杂度约为O(our models)=O(N2×O(RotatE))，其中N表示聚类数，相较于CTransR中的O(N3×O(TransR))有较低的时间复杂度。

2.3 理论分析

MSRE 方法在扩充语义表示的同时，也能保证模型处理复杂关系的能力，即不破坏原有的对称、反对称、逆、复杂等关系。证明如下：

（1）MSRE 能处理对称关系、反对称关系

3 实验结果与分析

3.1 数据集

Wikipedia上的通用数据集FB15K[27]和WordNet[30]的英文字典数据集WN18[31]常用于验证知识补全任务。由于FB15K 和WN18 中包含大量的逆关系，导致关系学习不平衡，弱化其他关系学习精度，采用仅保留每对互逆关系中一个关系的FB15K-237 和WN18RR数据集，其实体和关系分布情况如表1所示。

表1 数据集分布情况Table 1 Distribution of datasets

FB15K-237 的数据量远大于WN18RR，但其实体数量大约为WN18RR 的1/3，关系数量大约为WN18RR 的21 倍。可以看出，FB15K-237 数据集拥有较为复杂的实体与关系，可能存在更多的多语义现象。

3.2 实验设置

3.2.1 实验方案

本文采用链路预测和三元组分类任务验证提出的MSRE 算法。链路预测任务在已知关系、头实体、尾实体的情况下，根据已有的实体按照可能性（得分函数的大小）进行排序。三元组分类任务可以看作判断给定的三元组是否是正确的二分类问题，即引入阈值θ，将特定三元组得分与之相比判定是否有效，它被用来评价事实三元组的正确性。

在链路预测任务中设置两组实验：k值测试实验（k-test）和链路预测性能实验（link-prediction）。在三元组分类任务中设置三元组分类预测性能实验（triple-classification-prediction），如表2 所示。

表2 实验策略Table 2 Experiment strategy

MSRE 的主要思想是扩充关系的语义表达，但不同的关系簇数量的选择对模型的准确率有较大的影响，因此分别设定不同语义簇分量k值，其中k=1 为RotatE 的基线模型，考虑显存的限制，以{1,2,5}为间隔对比k∈(2,3,5,10)，并加入MSRE 进行链路预测任务，以验证语义分量簇的有效性。固定k值后再与TransE、DisMult、ComplEx、RotatE 四种方法对比。

3.2.2 参数设置

各模型的参数设置如表3 所示，针对本文提出的MSRE 方法，经过参数调优后，在FB15K-237 中设置batchsize 为256，负例数量256，关系向量维数设置为1 000，gamma 设置为9，学习率为0.000 01，max_steps设置为160 000。在数据集WN18RR 中设置参数batchsize 为256，负例数量为1 024，关系向量维数为500，gamma 值为6，学习率设为0.000 05，max_steps设为160 000。

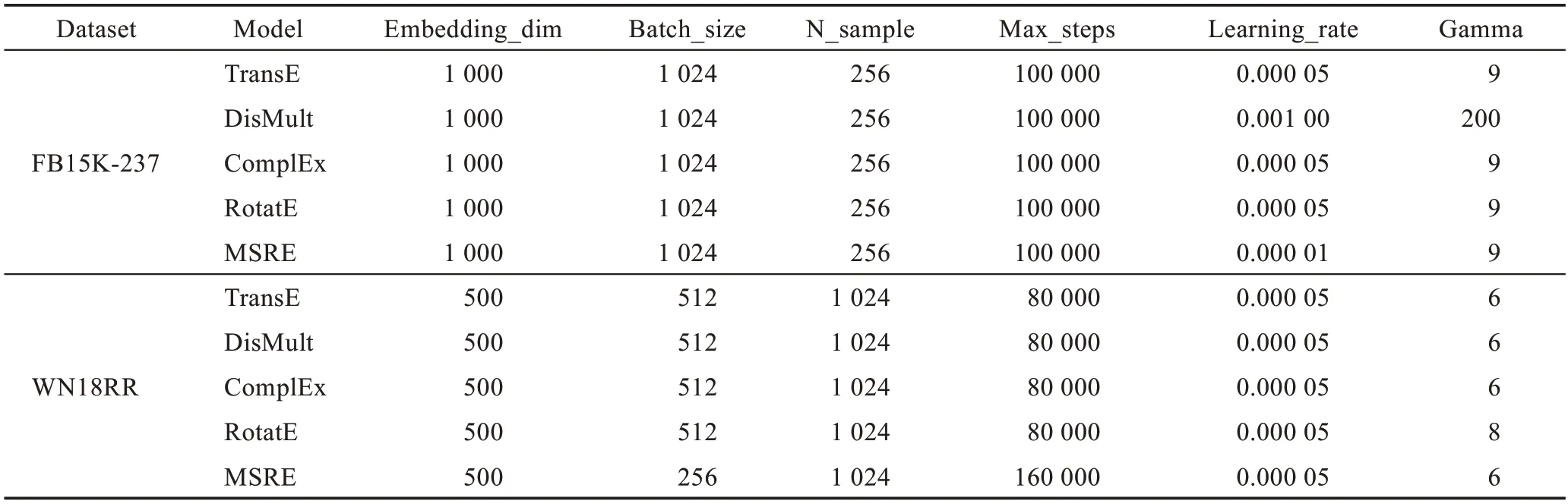
表3 各模型参数设置Table 3 Parameter setting of models

3.2.3 评价指标

链路预测任 务以MR、MRR、Hit@10、Hit@3、Hit@1 作为评价模型的指标，MR 表示平均排序，MRR 表示平均倒数排名，Hit@10 表示得分函数排序中前10 个命中三元组的百分比，Hit@3、Hit@1 分别表示命中前三个和第一个的百分比。三元组分类任务以TP（真阳性）、FP（假阳性）、Precision（准确率）作为实验指标。

3.3 实验结果

3.3.1 链路预测任务

链路预测任务中，k-test 实验结果如表4 所示，当语义簇分量设置为1（k=1）时，即为原始的RotatE模型，其Hit@10 值为0.533 0。k取值为2、3、5、10 为MSRE 方法中不使用MS（Mean-Shift）聚类的情况。可以看出，当k=3 时，Hit@10 值提升到0.539 0，相较于k=1（RotatE）提升了约0.006，随着语义分量数扩大，即k>3 后，Hit@10 值开始降低。MSRE 的Hit@10 值最高为0.540 0。根据表4 绘制Hit@10 结果图，如图3 所示。

表4 k-test实验结果Table 4 k-test experimental results

图3 k-test(k=1,2,3,5,10)对比实验结果Fig.3 Experimental results of k-test(k=1,2,3,5,10)

Link-prediction实验中，在FB15K-237和WN18RR数据集上应用MSRE 以及其他五种方法进行链路预测，实验结果如表5 所示。五种基线模型中，RotatE性能较优（MR 值为177，Hit@10 值为0.533），而相较于RotatE，本文提出的MSRE 方法在FB15K-237 数据集上Hit@10 指标提升了0.007，Hit@3 提升了0.006，并且MR 值由177 变为160，有一定程度的提升。

表5 Link-prediction 实验结果Table 5 Link-prediction experimental results

根据文献[7]对于多对一、一对多、多对多关系的定义，本文对验证集中的关系分别统计(h,r)和(r,t)的数量，并验证三种关系类型的Hit@10 值，如表6 所示。其中H 表示预测头实体任务，T 表示预测尾实体任务，A 表示求两者的平均值。

表6 FB15K-237 上三种关系的Hit@10Table 6 Hit@10 for three relationships on FB15K-237

实验结果显示，本文中的方法能够在多对一、多对多关系上有不错的性能提升。

3.3.2 三元组分类任务

由于FB15K-237、WN18RR 中提供的测试集都是正确的，需指定三元组分类任务中的无效三元组生成策略。为减少对训练过程无意义的负例三元组出现，将负例三元组定义为存在该关系的三元组实体的组合，其定义如下：

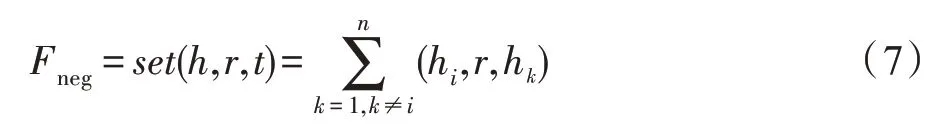
其中，θ的值依据Socher[8]中的方法，在最大化各关系的准确率前提下得到。如表7 所示，TP 表示实际为正例三元组且模型分类为正例的数量，FP 表示实际为负例三元组误分为正例的数量，Acc 表示模型分类为正例的三元组中实际为正例的比例。

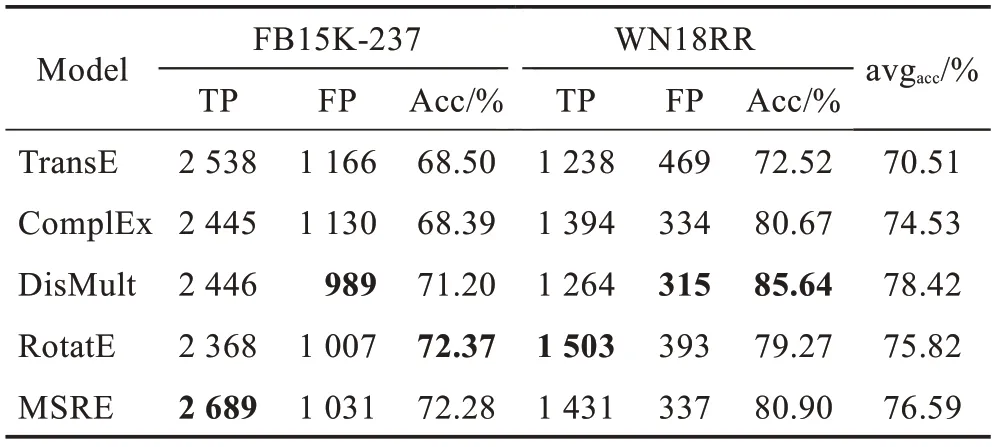
表7 三元组分类任务结果Table 7 Triple classification task results

通过实验结果分析发现，本文方法在FB15K-237数据集上精度比RotatE稍有降低，在数据集WN18RR上模型精确率有所提高，对比RotatE 提高了1.63 个百分点，但DisMult表现更好。

MSRE 方法通过细分关系向量，利用语义分量簇扩充原有的关系表示，以提升知识补全模型的关系表示能力。但随着关系语义分量的增多，易导致TP和FP 都同样增加。在FB15K-237 数据集中模型效果相对原模型有些许降低，分析原因为模型约束条件过少，需要挖掘各语义关系之间的约束以提升模型的辩错能力。从WN18RR 数据集中可以看出，MSRE方法相较于RotatE 有较大幅度的提升，但相对DisMult 模型效果较差，主要因为WN18RR 数据集中关系种类数较少，在关系种类数较少的情况下，DisMult模型中进行了关系向量与实体向量的矩阵运算，能够学到关系和实体更为复杂的交互。尽管MSRE 方法利用多语义方法进行扩充，由于各关系语义分量之间是通过自适应的聚类算法获得的，语义分量之间相互独立，缺乏语义之间的关联关系，导致辩错能力有所下降。

3.4 实证分析

为验证本文提出的MSRE 方法能够挖掘关系的多语义信息，通过对FB15K-237 数据集上训练后的实体和关系向量进行聚类，查看相同向量的不同语义分量是否具有语义相似性，即同一个关系向量下的各分量对应的三元组表达的语义是否相一致。如表8 所示，在名人关系中通过关系语义细分，分为两个语义分量簇，观察其中的三元组发现，两个语义分量簇体现为歌手间朋友关系和演员间朋友关系；运输方式关系的原有关系向量表示是单一的，通过关系语义细分，分为两个语义分量，其中一个分量描述的是实体为省会城市，另一个分量描述的是实体为非省会城市。省会城市运输工具种类较多，而非省会城市交通运输设施相对欠缺，由此挖掘出隐藏的关系信息。这样的语义信息在position 关系中同样有所体现。通过实证分析发现，MSRE 方法在关系语义细分的有效性。

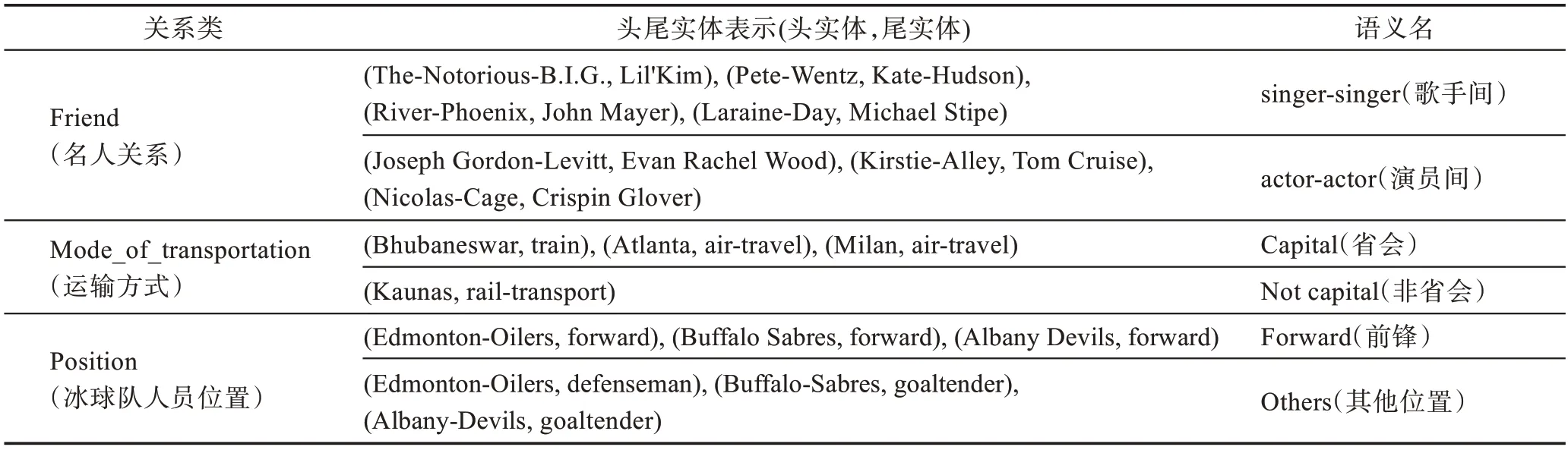
表8 语义分析Table 8 Semantic analysis

4 结束语

为解决关系多语义问题，本文从表示结构出发利用语义分量簇扩充原有的关系表示，修改原有的得分函数以自适应的方式挑选出最恰当的语义分量作为当前三元组的关系分量，其中语义分量簇的数量由模型自适应学习。本文提出的MSRE 方法在不破坏原有模型解决对称关系、反对称关系、逆关系、复杂关系的基础上，保证了向量在几何表示上一个关系对应一个向量的唯一性。链接预测、三元组分类等实验证明，提出的方法不仅能够自动获取关系的多语义簇，为实体对选择最合适的关系语义，且在解决一对多、多对一问题上提出了一个关于关系细分角度的方法。下一步工作将考虑加入实体的层次性，丰富实体表达，并尝试并入多路径关系，增强复杂关系表示能力。同时，在链路预测任务中引入节点的置信度，用以提高模型的准确度，从而解决更为复杂的关系补全问题，并将其应用于大规模的知识图谱中。