基于ACGAN和模型融合的电机轴承故障诊断方法

李俊卿， 胡晓东， 耿继亚， 马亚鹏

(华北电力大学 电气与电子工程学院，河北 保定 071000)

0 引 言

轴承是电机中最易损伤的元件之一，对其故障进行诊断可以有效减少因故障停机而造成的经济损失[1]。目前轴承故障诊断方法主要集中于对振动信号的提取和分析[2-4]，但是传统的信号分析方法依赖大量的先验知识，导致诊断效率低、工作量大[5]。因此，如何高效精确地提取并识别故障特征成为当今的研究热点。

大数据时代的到来为故障诊断提供了新的思路，以机器学习为代表的人工智能算法已经广泛应用于各种设备的故障诊断，并取得了不错的效果。文献[6]通过结合多个AlexNet基分类器和Adaboost算法对多工况下的滚动轴承故障进行识别。文献[7]在传统集合经验模态分解的基础上，引入了深度学习中的长短时记忆(LSTM)网络，并通过主成分分析法(PCA)对分解后的分量进行降维，有效提高了故障诊断的准确率。文献[8]提出了一种基于Inception-ResNet模型的方法对轴承故障进行分类，通过引入三维卷积融合了模型中各个通道的信息，在提高故障诊断能力的同时提升了训练效率。

虽然以上方法都取得了不错的效果，但是这些智能算法均基于大量的平衡样本数据，当样本数据不足时，往往难以达到预期的效果[9]。适当运用生成式对抗网络(GAN)可以很好地解决数据不足以及数据不平衡的问题，但是传统GAN存在训练困难的问题，需要加以改进。文献[10]提出了一种梯度惩罚Wasserstein生成对抗网络(WGAN-GP)，增强了网络训练的稳定性，但该方法需要人工生成带标签的数据信息。文献[11]利用条件生成式对抗网络(CGAN)模型生成带标签信息的数据，将GAN模型由无监督转变为有监督。文献[12]利用深度卷积生成对抗网络(DCGAN)生成齿轮点蚀图像，有效解决了齿轮疲劳试验成本高、故障样本不充分等问题。文献[13]通过训练信息生成对抗网络(InfoGAN)生成时频图像，并生成了更多的图像样本。辅助分类器生成对抗网络(ACGAN)[14]结合了CGAN和InfoGAN的优点，极大程度地弥补了GAN模型训练困难的缺点，并且可以生成指定目标类别的高质量数据。

集成学习[15]是机器学习的一种算法，通过集成众多评估器的预测信息得出结果，这种算法中的各个弱评估器无法单独得出较理想的结果。与狭义集成算法不同，模型融合虽然并未包含太多的评估器，但被融合的各个评估器都具有强学习能力，经过适当融合可提高诊断结果的准确率。常见的模型融合方法主要有均值法、投票法[16]和堆叠法[17]。

基于此，本文提出基于ACGAN和模型融合的电机轴承故障诊断方法。为了克服ACGAN处理一维信号时可能会造成特征信息丢失的问题，本文首先将一维振动信号转换为二维灰度图像。然后通过构建ACGAN对原始样本进行数据扩充，生成高相似度的故障数据样本。最后将生成样本与原始样本混合并通过PCA进行数据降维后训练融合模型，再将其应用于电机轴承故障诊断。

1 模型原理

1.1 GAN

GAN由生成器和判别器组成，如图1所示。生成器通过学习真实样本的分布生成样本；判别器是一个二分类器，用于判别输入的数据是真实数据还是生成器生成的数据。两者在训练过程中通过竞争最终达到纳什均衡。

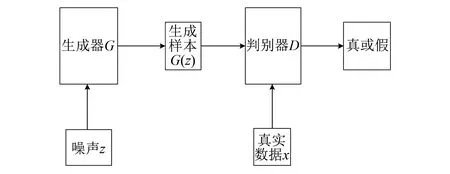
图1 GAN原理示意图

判别器和生成器在训练时的目标函数如下所示：

V(D,G)=Ex～PxlogD(x)+

Ez～Pzlog{1-D[G(z)]}

(1)

式中：V(D,G)为目标函数；E为期望；下标x代表真实样本；下标z代表输入生成器的噪声信号；G(z)为生成样本；D为判别器的输出；Px为真实数据分布；Pz为噪声数据分布。

判别器的目标是在G给定的条件下使V最大，生成器的目标是在D给定的条件下使V最小。两者交替迭代训练，最终目标函数趋于收敛，即达到纳什均衡，此时生成器可以生成令判别器无法辨别的数据样本。

1.2 ACGAN

理论上GAN通过训练最终会达到纳什均衡，但是GAN存在梯度消失，会导致训练困难，因此需要对传统GAN加以改进。ACGAN就是一种衍生的优化模型，其原理如图2所示。

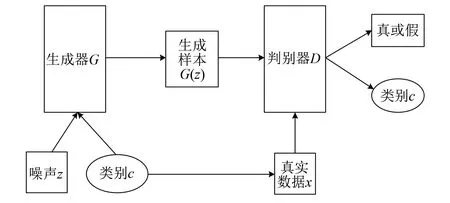
图2 ACGAN原理示意图

ACGAN在训练时不仅使用标签信息，同时也重建标签信息。生成器的输入为随机噪声数据和标签信息，通过拼接两者提取特征进而生成样本，判别器的输入为生成数据或者真实数据，输出为真假判断结果和分类结果。因此，ACGAN的损失函数由两部分组成，一部分为判断真假的损失函数Ls，用式(2)描述，一部分为判断类别的损失函数Lc，用式(3)描述：

Ls=E[logP(S=real|Xreal)]+

E[logP(S=fake|Xfake)]

(2)

Lc=E[logP(C=c|Xreal)]+

E[logP(C=c|Xfake)]

(3)

式中：Xreal为真实数据；Xfake为生成器生成数据；S、C为判别结果；c为类别。

1.3 堆叠法

堆叠法是模型融合中最热门的方法，主要有融合效果好、可解释性强和适用于复杂数据等优点。堆叠法模型为两层结构，如图3所示。第一层为多个具有强学习能力的基学习器；第二层为较简单的元学习器，通过训练得到各个基学习器的最佳融合规则。

图3 堆叠法结构示意图

2 基于ACGAN和模型融合的电机轴承故障诊断方法

基于ACGAN和模型融合的电机轴承故障诊断方法分为故障样本生成和故障诊断两个部分。首先构建并训练ACGAN，使其能够产生与真实数据高度拟合的样本；然后将平衡后的数据输入融合模型进行训练，最终得到高精度的故障诊断模型。

2.1 ACGAN模型

本文使用的ACGAN模型包含一个生成器和一个判别器。生成器采用3层结构，分别为输入层、隐藏层和输出层，输入层和隐藏层均使用BatchNorm层防止梯度消失或梯度爆炸；判别器由输入层、3个隐藏层和2个输出层构成，输入层和输出层均包含dropout层。具体结构如表1所示。

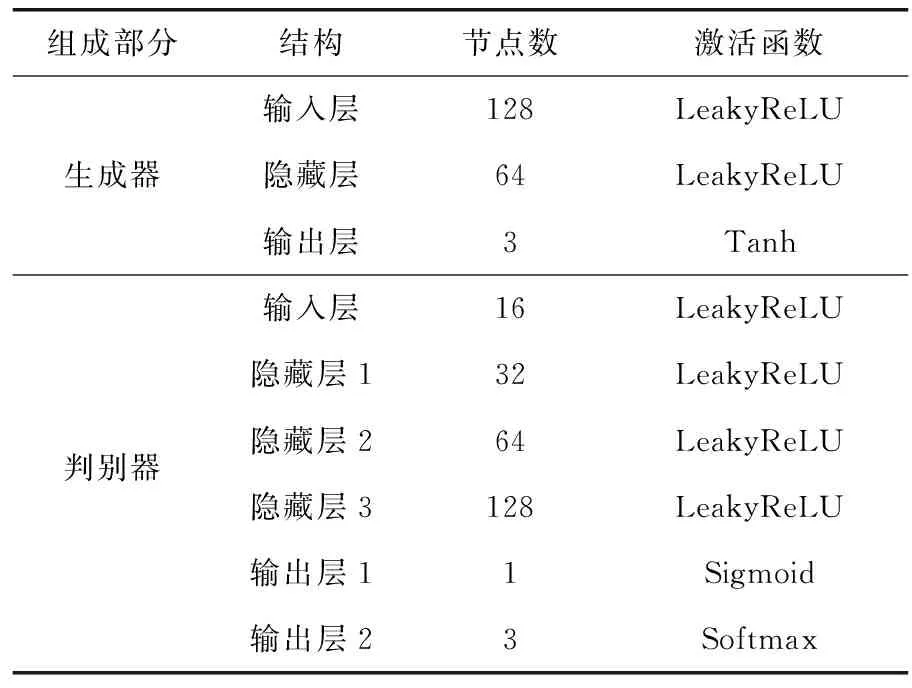
表1 ACGAN结构

2.2 基于模型融合的故障诊断模型

采用的模型融合方法为堆叠法，选择的基学习器分别为逻辑回归模型(LR)、随机森林(RF)、梯度提升(GB)、决策树(DT)、XGBoost和K近邻算法(KNN)。为了避免过拟合，元学习器选择较为简单的RF分类器。

融合模型的训练及测试过程如图4所示，首先将数据集{S，Y}分为训练集S1和测试集S2，Y为数据标签，并且按照5折交叉验证，将训练集S1分为5个子集：{S11，S12，S13，S14，S15}。在某个基学习器训练时，其中4个子集作为训练数据，剩下一个作为验证数据，最后每个基学习器会输出对应的验证结果，将这些验证结果拼接成新的矩阵Yp用于训练元学习器。训练完毕后，将测试数据S2输入各个基学习器中得到不同的预测结果，将各个基学习器的预测结果输入元学习器中，得到的预测结果即为融合模型的测试结果。

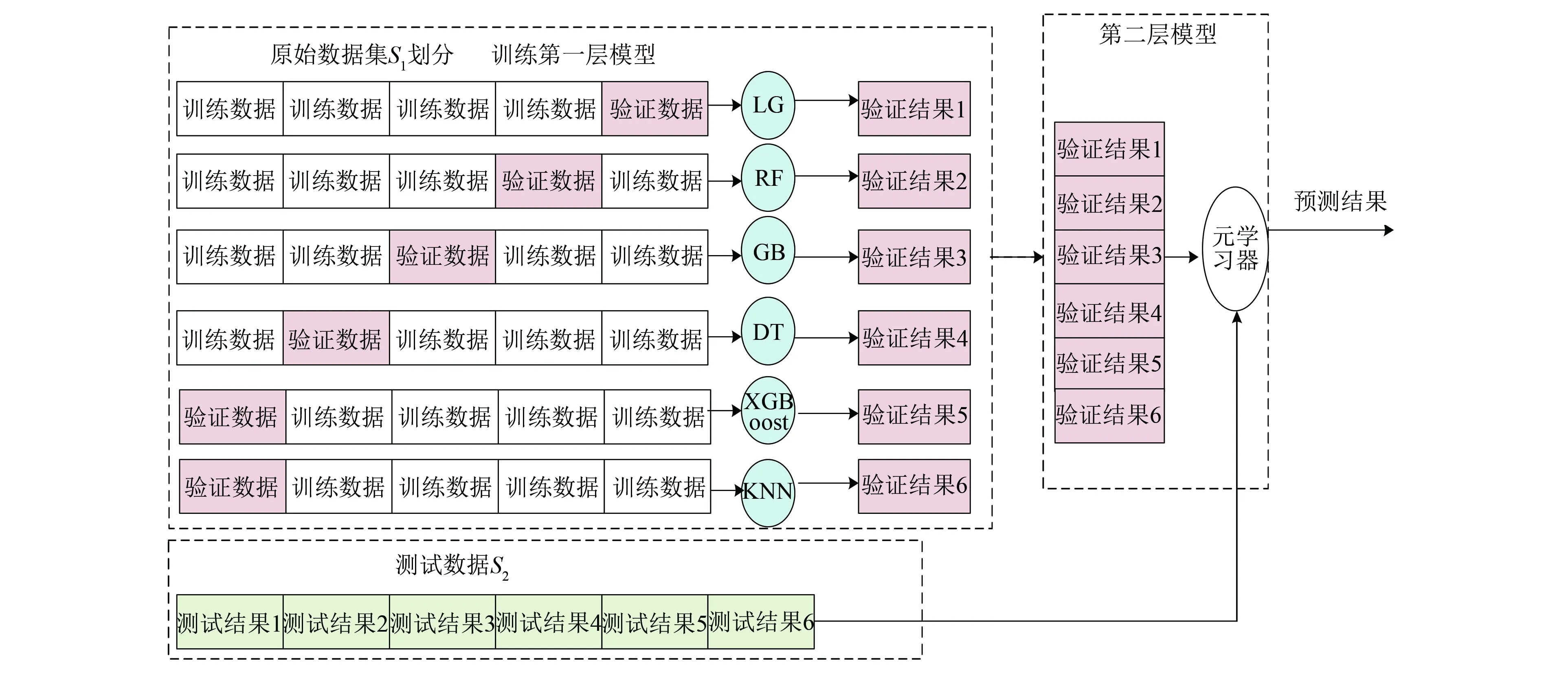
图4 堆叠法融合训练和测试框架

2.3 方法流程

本文所提的故障诊断方法包括数据采集和处理、生成样本与故障诊断三个阶段，具体的流程如图5所示。

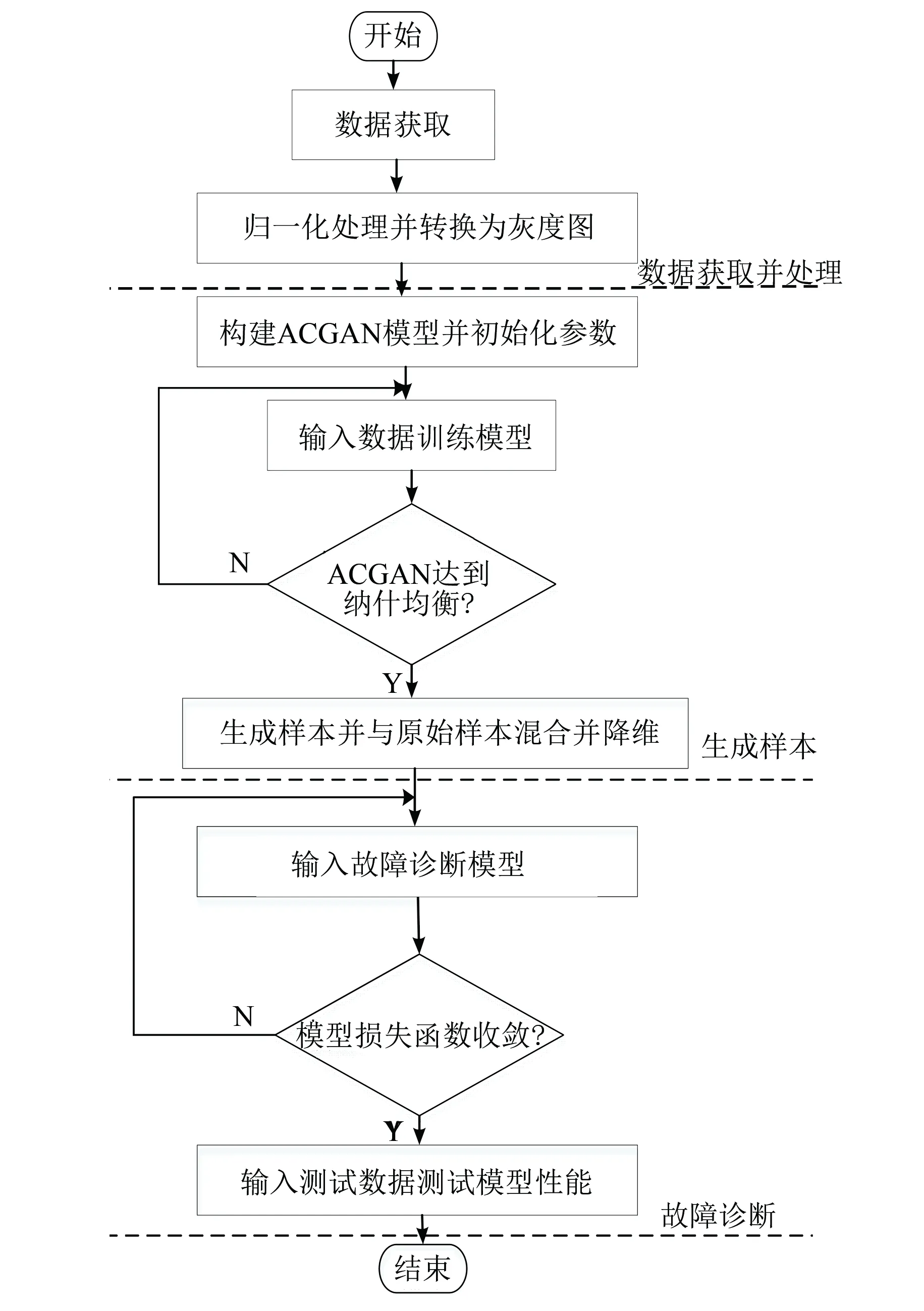
图5 本文方法流程图

本文方法首先收集电机轴承各状态下的数据，对数据进行归一化处理并将其转换为二维灰度图；给灰度图加上标签并乱序，然后输入ACGAN进行训练，直至生成器和判别器达到纳什均衡；用生成器生成的新样本与原始样本混合并降维，输入故障诊断模型进行训练，当损失函数收敛后，用测试集验证模型的诊断效果。

3 试验验证

3.1 数据说明

本文数据来源为美国凯斯西储大学的轴承试验数据，包括了内圈故障、外圈故障、滚动体故障和正常状态四种类型下的数据集。数据采样频率为12 kHz，电机转速为1 797 r/min，空载运行，损伤直径为0.017 78 cm。

3.2 基于ACGAN生成样本

首先将各个状态的数据通过滑动时窗的方式转换成如图6所示的二维灰度图，以4 096个数据点为一组生成的64×64的灰度图作为一个样本。此方法在最大程度上保留了一维数据的二维特征，并且不需要预处理参数，减少了对技术人员经验的依赖[18]。

图6 二维灰度图

构建ACGAN模型并初始化模型参数。使用内圈故障、外圈故障、滚动体故障和正常状态各500个样本输入模型中训练。采用的判别器为三层隐藏层，其在判别能力增强的同时可能会压制生成器，从而出现不能为生成器提供有效指导的现象。为了防止出现这种情况，在训练初期，训练多次生成器后训练一次判别器，当生成器生成能力较强时，恢复两者各训练一次。生成器和判别器的损失函数如图7所示，可以看出，当迭代次数在1 000次左右时，损失函数趋于收敛，此时停止训练并用ACGAN生成足够的样本数据。

图7 生成器与判别器的损失函数

3.3 数据处理

数据集划分：将生成器生成的数据与原始数据混合后按7…3的比例划分为训练集和测试集，并以独热编码的形式为不同状态的数据打上不同的标签。

PCA数据降维：数据维度过高时，数据中的冗余信息往往会使得特征提取困难和训练速度慢，因此在训练故障诊断模型前，通过PCA将数据降维以提高模型训练的速度和诊断的准确率。

3.4 基于模型融合的故障诊断

将处理后的训练样本输入上述的融合模型中，为了验证本文所提方法的有效性，比较了融合模型以及每个基学习器单独作为诊断模型时在三种样本下的诊断准确率。其中三种样本划分情况如下所示。

(1) 样本1：总样本个数为1 200个。不使用ACGAN生成样本，四种状态的真实样本各300个；

(2) 样本2：总样本个数为8 000个。不使用ACGAN生成样本，四种状态的真实样本各2 000个；

(3) 样本3：总样本个数为8 000个。使用ACGAN生成四种状态样本各1 500个，并与原始数据中四种状态各500个样本混合，最终样本中包含四种状态各2 000个。

样本1、样本2和样本3均按7:3的比例划分为训练集和测试集，并且将三种样本进行PCA降维处理。三种样本下各种模型的诊断准确率如表2所示。

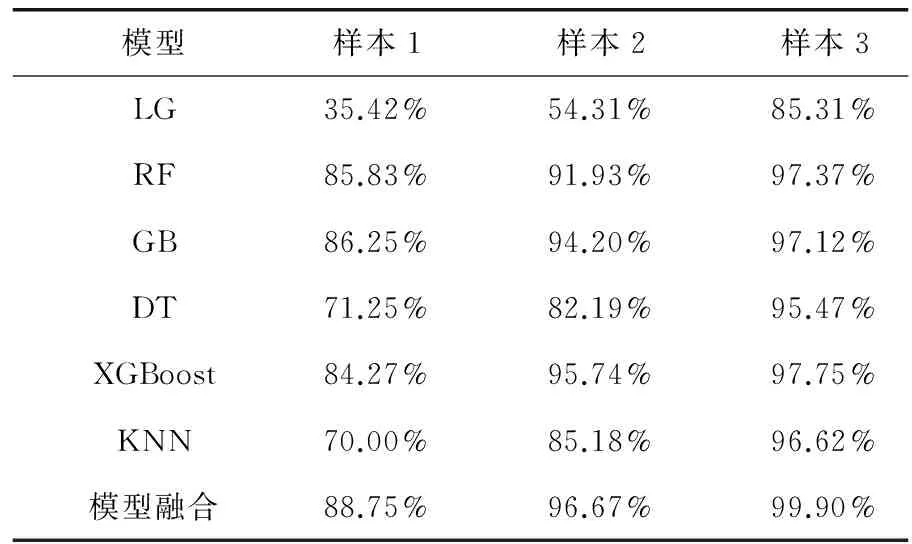
表2 不同模型在不同样本下的诊断准确率

由表2可以得出如下结论：

(1) 对各个基学习器和融合模型的诊断准确率进行比较，可以看出，融合模型的准确率明显大于任何一个基学习器，证明了模型融合的必要性和有效性；

(2) 比较样本1和样本2的结果，由各个模型在样本2上的表现可以看出，当数据量大且样本平衡时，模型的诊断正确率较高，而数据量较少的样本1则无法有效训练模型，导致模型的诊断效果不佳；

(3) 比较样本1和样本3的结果，模型在数据量少的样本1上的诊断准确率明显低于在样本3上的准确率，说明训练模型需要足够的数据，而本文所提的ACGAN模型可以解决训练数据不足的问题；

(4) 比较样本2和样本3的结果可以看出，当训练样本数量相同时，由ACGAN生成的样本对模型的训练效果更好，原因是采集的原始数据包含较多的噪声和冗余信息，这些噪声会影响模型对特征提取的速度和准确度，而ACGAN在生成样本之前已经对原始数据进行了一次特征提取，所以生成的数据比原始数据所含噪声少得多，因此模型在样本3上的表现要优于在样本2上的表现。

综上，本文所提的基于ACGAN和模型融合的电机轴承诊断方法大大提高了故障诊断的准确率。

4 结 语

本文将电机轴承不同运行状态的数据集转换成二维灰度图并标签化，通过训练ACGAN从而生成样本，将扩充后的样本经过PCA降维后训练融合后的模型。通过比较不同样本以及不同模型下的故障诊断准确率，证明了本文所提方法的优越性。ACGAN和模型融合方法的优势主要有：

(1) 利用ACGAN生成与原始样本高度拟合的样本，实现对数据的扩充，解决了数据不平衡和数据不足的问题；

(2) 数据处理中引入了二维灰度图和PCA数据降维，前者在最大程度上保留了数据的特征，减少数据信息丢失问题；后者将高维度的数据映射到低维度，在保留特征的同时减少了无效信息，提升了模型学习的效率；

(3) 引入了模型融合概念，对传统机器学习中具有强学习能力的算法通过堆叠法进行融合，利用RF算法找到最佳融合规则，大大提高了故障诊断的正确率。