永磁同步电机并联法模型预测转矩控制*

李耀华， 张鑫泉， 董国庆， 邓益志， 李茂盟， 童瑞齐， 丁 红， Rajibul Islam

(长安大学 汽车学院，陕西 西安 710064)

0 引 言

永磁同步电机(PMSM)有限状态集模型预测转矩控制(FCS-MPTC)将电机与逆变器视为一体，根据两者的离散模型和电机当前控制变量的状态，遍历逆变器所有电压矢量，对未来时刻的电机控制变量进行预测，通过体现控制目标的成本函数评估电压矢量，从而选择最优电压矢量作用于电机。由于MPTC概念清晰、控制直观，具有较强的柔性，可实现多变量协同控制和非线性约束，其近年来受到广泛关注[1-5]。MPTC的控制变量为不同量纲的磁链和转矩，需要设置和调整权重系数来平衡磁链控制和转矩控制。但目前暂无权重系数设计和调节的理论解决方法，大多采用试验法，其过程繁琐[6-7]。为了解决权重系数设计和调整问题，文献[8-11]采用模糊控制动态调节权重系数，但模糊控制规则的设计较为复杂。文献[12-14]采用粒子群算法和神经网络算法实现权重系数的调整，但需要构造大量训练数据集且算法自身计算量较大。

设计无权重系数的MPTC也是解决方案之一。文献[15-16]利用无差拍控制计算得到下一时刻的期望电压矢量或定子磁链矢量，将磁链和转矩转换为同量纲的控制变量，但无差拍控制计算较为复杂。文献[17]将磁链和转矩转换为相对误差率，但如果存在含控制目标的参考值，如开关次数不确定，仍需设计权重系数。文献[18-20]对各控制变量独立排序，成本函数为无量纲的排序位置，但排序计算量较大。

改变成本函数结构形式是无权重系数路径之一。文献[21-22]将多目标成本函数加权求和形式转换为单目标成本函数级联形式，从而消除权重系数。文献[23-24]将其转换为单目标成本函数电压矢量集合求交集形式。

本文建立PMSM并联法MPTC，研究磁链控制电压矢量集合和转矩控制电压矢量集合的电压矢量个数对系统控制性能的影响，进一步建立考虑开关次数控制的并联法MPTC，并采用模糊控制器动态调节开关次数，控制电压矢量集合的电压矢量个数。仿真结果验证了PMSM并联法MPTC可实现无权重系数，并可根据系统实时运行状态动态调整控制目标集合电压矢量的个数，优化系统控制性能。

1 PMSM MPTC

定子坐标系下，表面式PMSM磁链和转矩预测模型如下所示：

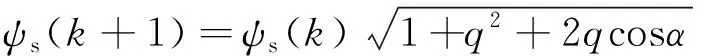
(1)

(2)

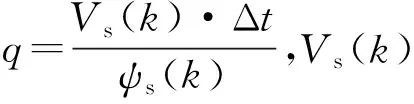
两电平电压源逆变器可产生8个开关状态，对应备选电压矢量集合如下所示：

Vs∈{V0,V1,V2,V3,V4,V5,V6}

(3)

式中：零电压矢量V0可由开关状态000或111生成，具体以开关次数最小原则选择[24]。

PMSM MPTC成本函数如下所示：

(4)

PMSM MPTC系统将7个电压矢量遍历代入磁链和转矩预测模型，得到下一时刻磁链和转矩的预测值，再基于成本函数得到7个电压矢量的控制效果，并选择令成本函数最小的电压矢量输出，系统框图如图1所示。

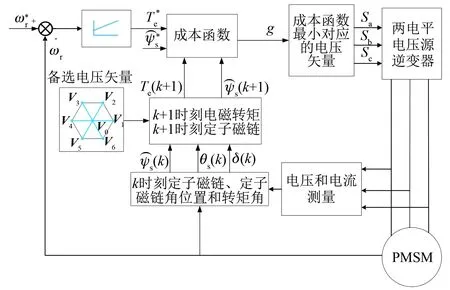
图1 PMSM MPTC系统

2 PMSM并联法MPTC

由上文可知，由于磁链和转矩的量纲不同，传统PMSM需要设计和调整权重系数，而权重系数的设计与调整较为复杂。因此，将多控制目标成本函数加权求和形式转换为独立的成本函数电压矢量集合求交集形式，可避免成本函数的设计与调整。

定义转矩控制成本函数和磁链控制成本函数分别如下所示：

(5)

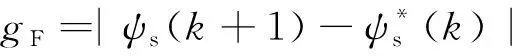
(6)

将7个电压矢量遍历代入转矩模型和磁链模型，可得到下一时刻转矩和磁链的预测值，再将其代入式(5)和式(6)，可分别得到7个转矩控制成本函数和磁链控制成本函数。设转矩控制电压矢量集合VT有m个电压矢量(1≤m≤7)，磁链电压矢量集合VF有n个电压矢量(1≤n≤7)。根据转矩控制和磁链控制成本函数，从小到大依次对VT和VF分别输出m个和n个电压矢量。对VT与VF求交集，根据交集的情况输出电压矢量。如果VT和VF交集为空集，则输出VT中磁链控制成本函数最小的电压矢量。如果VT和VF交集非空集，则输出交集中转矩控制成本函数最小的电压矢量。

PMSM并联法MPTC算法流程图和系统框图分别如图2和图3所示。

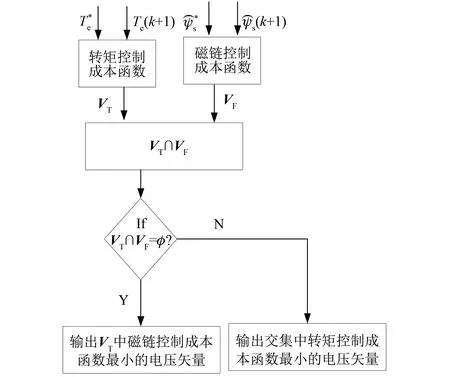
图2 PMSM并联法MPTC算法流程图

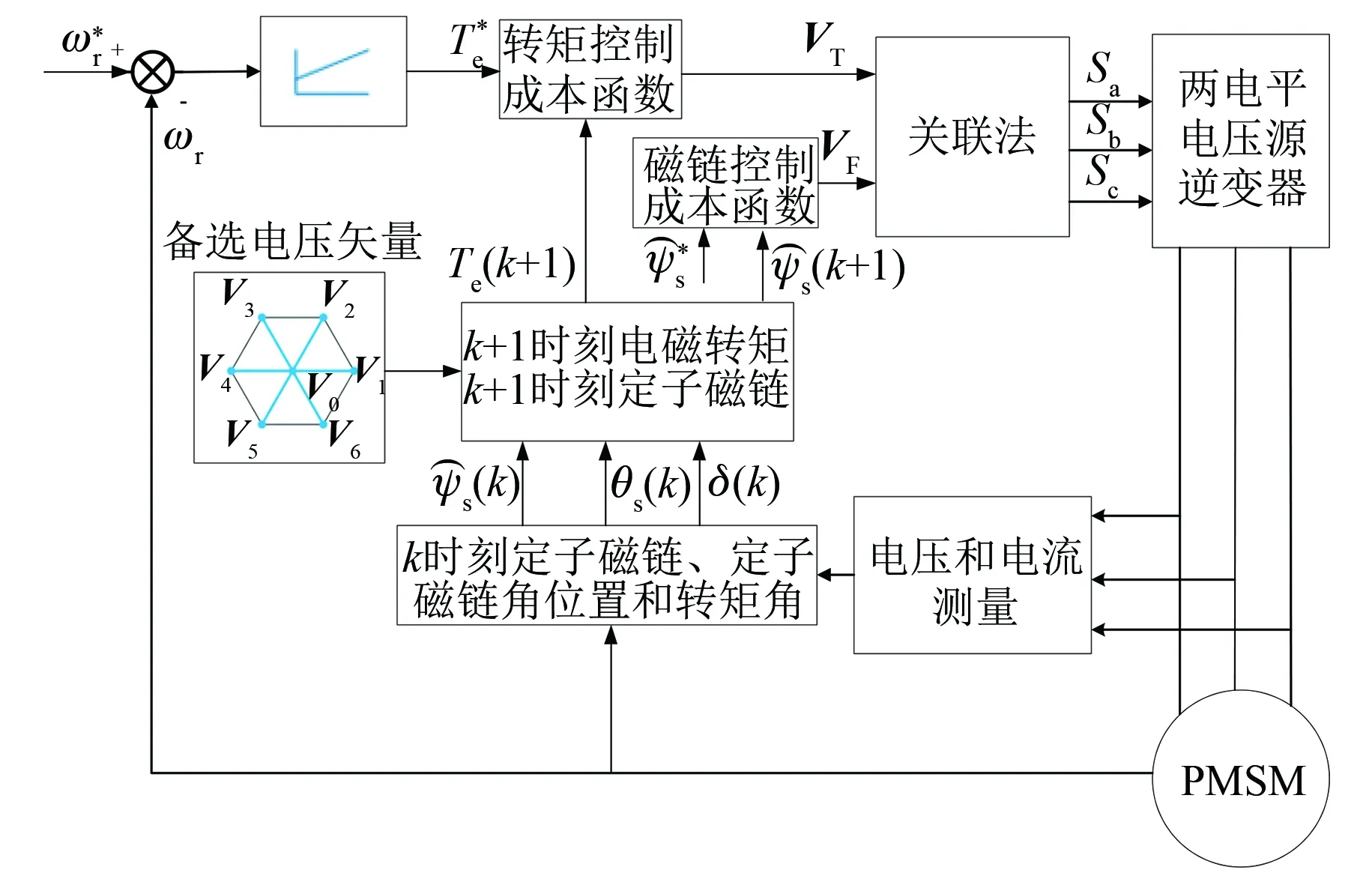
图3 PMSM并联法MPTC系统

基于MATLAB/Simulink建立PMSM并联法MPTC系统仿真模型。仿真模型为离散模型，采样周期为5×10-5s。直流母线电压为312 V，转速PI调节器参数为KP=50，KI=10，PI调节器输出区间为[-30 N·m，30 N·m]。电机参考转速初始为500 r/min，2 s时阶跃至-500 r/min；负载转矩初始为10 N·m，1 s阶跃至-10 N·m，3 s阶跃至10 N·m。仿真总时长为4 s。参考定子磁链幅值为0.3 Wb。仿真用PMSM参数如下：定子电阻Rs=0.2 Ω，定子电感Ld=Lq=0.008 5 H，永磁体磁链ψf=0.175 Wb，电机极对数p=4，额定转速750 r/min，额定转矩12 N·m，额定功率0.94 kW。

以m=n=3为例，PMSM并联法MPTC仿真波形如图4～图6所示。

图4 PMSM并联法MPTC仿真的电机转速

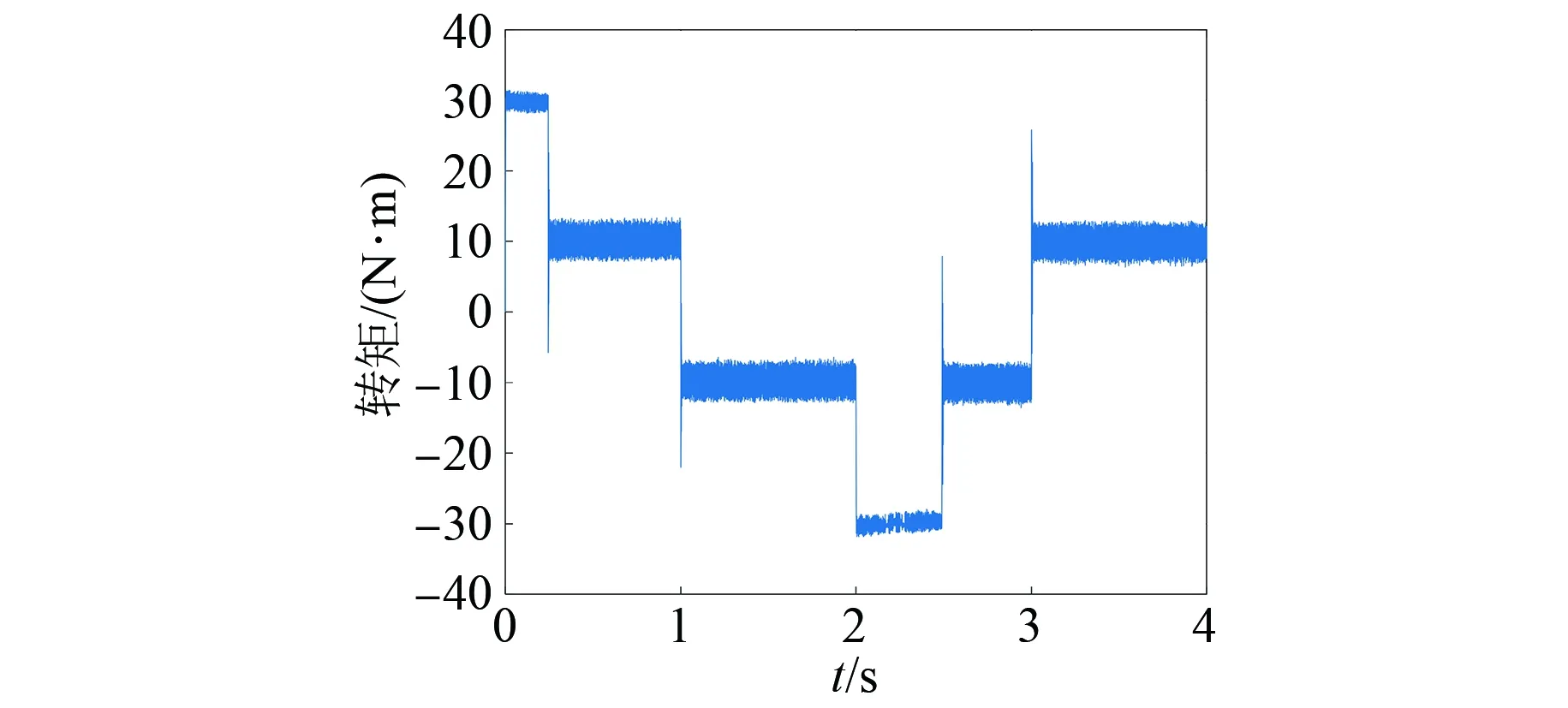
图5 PMSM并联法MPTC仿真的电机转矩

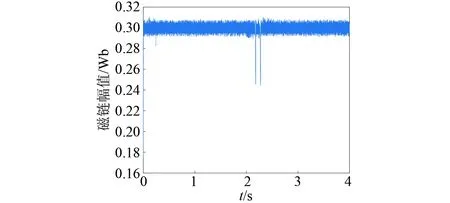
图6 PMSM并联法MPTC仿真的定子磁链幅值

定义转矩脉动均方根误差(RMSE)和磁链脉动RMSE如下所示：

(7)

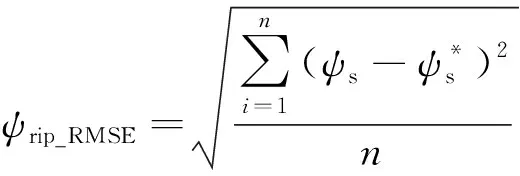
(8)

式中：n为采样个数。

m=1,2,3…,7，n=1,2,3…,7，PMSM并联法MPTC系统控制性能如表1所示。

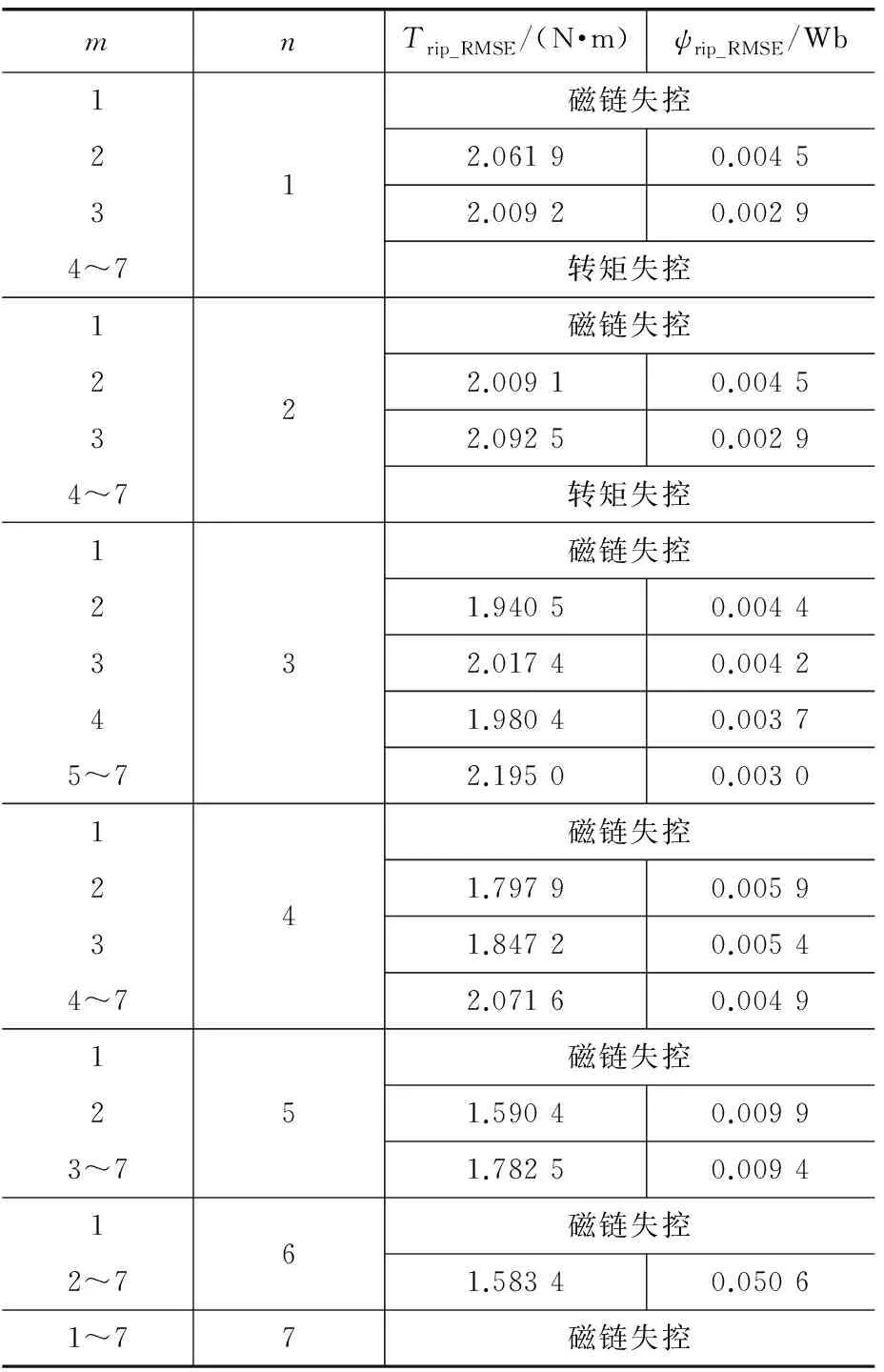
表1 并联法MPTC性能

基于式(4)建立传统MPTC系统，相同权重系数下，经试验法确定权重系数λ=50，此时电机系统控制性能如表2所示。

表2 传统MPTC性能

由仿真结果对比分析可知：

(1) 随着磁链集合电压矢量个数的增加，转矩脉动减小，磁链脉动增大；随着转矩集合电压矢量个数的增加，转矩脉动增大，磁链脉动减小。对于并联法，增加某一控制目标集合电压矢量的个数，则弱化对该控制目标的控制，该目标的控制性能变差。

(2) 当m+n>7，则VT与VF必定有交集，输出交集中转矩控制成本函数最小的电压矢量，此时增加m对输出的电压矢量没有影响。

(3) 当m=n=3，PMSM并联法MPTC与权重系数等于50的传统MPTC性能基本相当。

3 考虑开关次数的并联法MPTC

对于PMSM MPTC，可将开关次数控制也作为其控制目标之一。如上文分析，当控制目标较多时，并联法需确定各控制目标输出电压矢量集合并对电压矢量求并集，计算量较大，故控制目标不宜过多。因此，本文将磁链和转矩控制统一为性能控制，同时考虑开关次数控制，性能控制成本函数和开关次数控制成本函数分别如下所示：

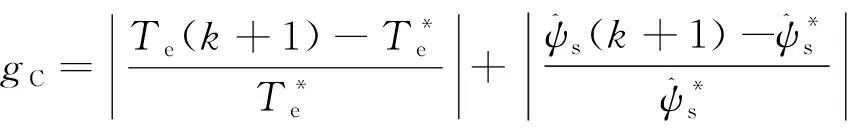
(9)

gS=2×[|Sa(k)-Sa(k-1)|+|Sb(k)-

Sb(k-1)|+|Sc(k)-Sc(k-1)|]

(10)

式中：Sa(k)、Sb(k)和Sc(k)为备选施加电压矢量对应开关状态；Sa(k-1)、Sb(k-1)和Sc(k-1)为上一时刻开关状态。

由式(10)可知，开关次数与备选电压矢量、上一时刻开关状态有关。备选电压矢量集合如下所示：

Vs∈{V0,V1,V2,V3,V4,V5,V6，V7}

(11)

式中：V0和V7为零电压矢量，分别对应开关状态000和111。

由于两电平逆变器开关状态确定且有限，基于上一时刻的电压矢量，备选电压矢量的开关切换次数是已知确定的，如表3所示。因此，可根据上一时刻的电压矢量，直接查表获取8个电压矢量对应的开关次数，无需计算。

表3 开关次数控制成本函数表

将8个电压矢量代入式(9)可得到8个性能控制成本函数，基于上一时刻的电压矢量和表3，可得到8个开关次数成本函数。根据性能控制成本函数和开关次数成本函数大小，从小到大对性能控制电压矢量集合VC和开关次数电压矢量集合VS分别输出m个和n个电压矢量，其中1≤m≤7，1≤n≤7。由表3可知，VS存在开关次数相同的情况， 因此n取值只有1、4、7、8四种情况。将VC与VS求交集，根据交集的情况输出电压矢量。如果VC和VS交集为空集，则输出VC中性能控制成本函数最小的电压矢量。如果交集非空集，则输出交集中性能控制成本函数最小的电压矢量。考虑开关次数的PMSM并联法MPTC系统如图7所示。

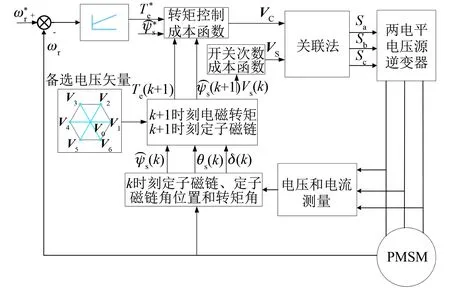
图7 考虑开关次数的PMSM并联法MPTC系统

上文相同仿真条件下，以m=3，n=4为例，考虑开关次数的PMSM并联法MPTC仿真波形如图8～图10所示。

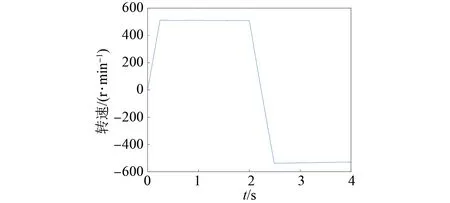
图8 考虑开关次数后仿真的电机转速

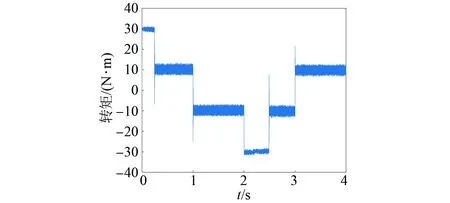
图9 考虑开关次数后仿真的电机转矩

图10 考虑开关次数后仿真的定子磁链幅值

定义平均开关频率如下所示：

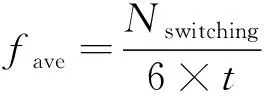
(12)

式中：Nswitching为开关次数；t为仿真时间。

m=1,2,3,…,8，n=1，4，7，8，考虑开关次数的PMSM并联法MPTC系统性能如表4所示。

表4 考虑开关次数的PMSM并联法MPTC性能

基于下式建立传统MPTC系统，相同权重系数下，经试验法确定权重系数λ=0.005，此时电机系统控制性能如表5所示。

gC=gC+λ·gS

(13)

表5 传统MPTC性能

由仿真结果对比分析可知：

(1) 随着m的增加，开关频率减小，控制性能变差；随着n的增加，开关频率增大，控制性能变好。

(2) 当m+n>7，则VC与VS必定有交集，输出交集中性能控制成本函数最小的电压矢量，此时增加m对输出的电压矢量没有影响。

4 模糊并联法MPTC

由上文可知，m和n的个数影响系统性能，可利用这一特征根据电机实时状态动态调节m或n的大小，在磁链和转矩脉动较大时，使系统侧重提升控制性能，磁链和转矩脉动较小时，使系统侧重减小开关频率，从而适应动态变化的电机运行状态。

对于考虑开关次数的并联法MPTC，VS的电压矢量个数n只有1、4、7、8四种选择，较为简单，故选择n作为动态调整变量。随着n的增加，开关频率增大，控制性能变好，采用模糊控制器动态调整n的大小，优化系统控制性能。由上文可知，m=3时，系统整体性能较好。因此，令m=3，由模糊控制器调节n。模糊控制器的输入为转矩误差绝对值和磁链误差绝对值，输出为VS的n。转矩误差绝对值论域为[0 N·m, 2 N·m]，分为3个模糊子集{Ts,Tm,Tb}，隶属度函数μ(T)如图11所示。磁链误差绝对值论域为[0 Wb, 0.02 Wb]，分为3个模糊子集{Fs,Fm,Fb}，隶属度函数μ(F)如图12所示。n的输出论域为[0, 9]，分为4个模糊子集{n1,n2,n3,n4}，隶属度函数μ(n)如图13所示。

图11 转矩误差绝对值隶属度函数

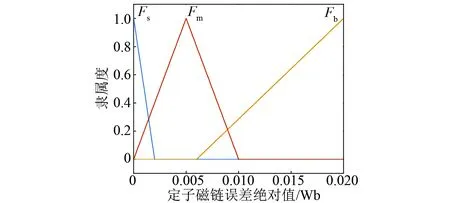
图12 磁链误差绝对值隶属度函数

图13 VS电压矢量个数n隶属度函数

模糊控制规则如表6所示。经过Mamdani模糊推理规则后，采用最大隶属度去大法解模糊并输出;再采用最大隶属度平均法解模糊并输出。PMSM模糊并联法MPTC系统如图14所示。相同仿真条件下，PMSM模糊并联法MPTC系统仿真结果如图15～图18所示。

表6 模糊控制规则表

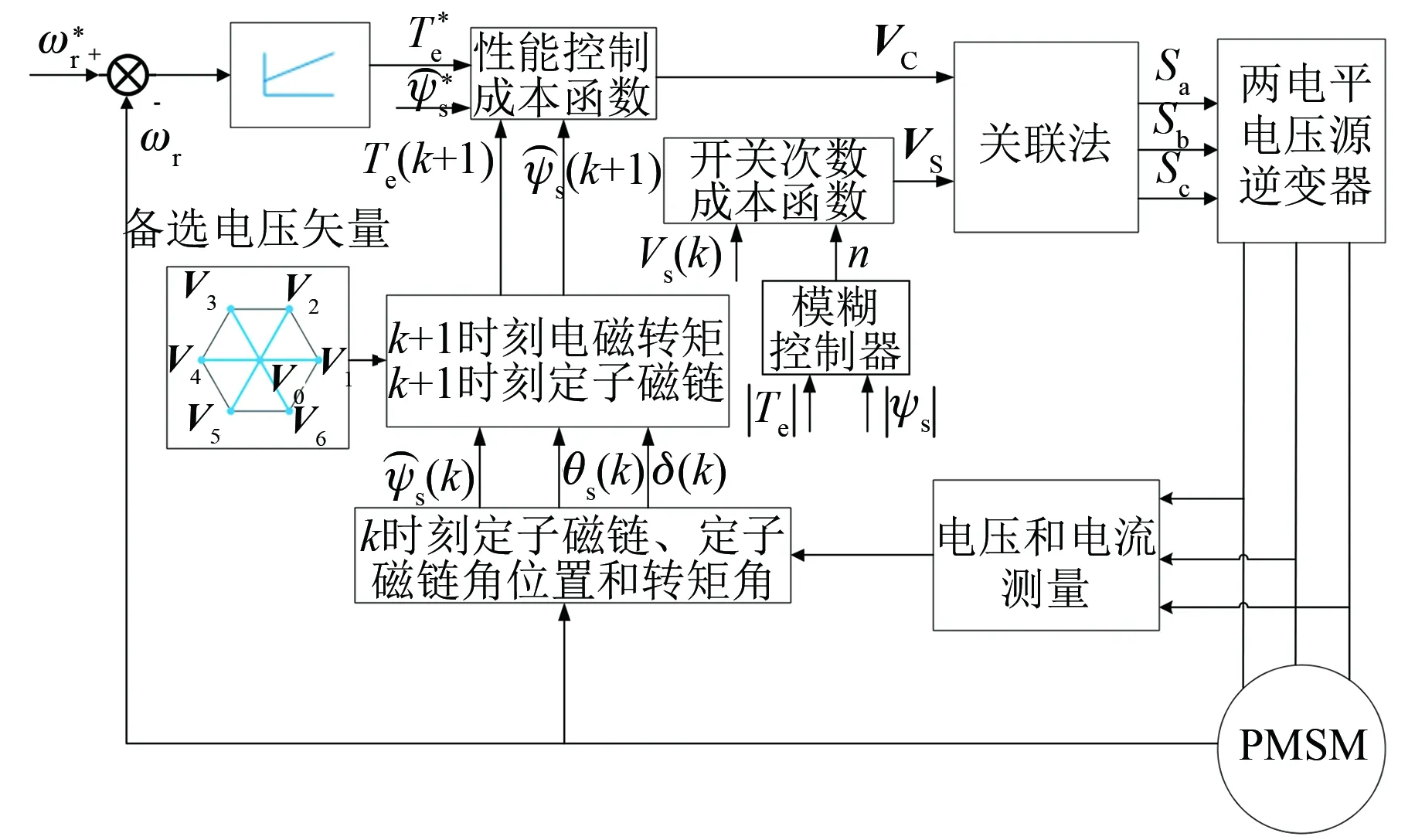
图14 PMSM模糊并联法MPTC系统

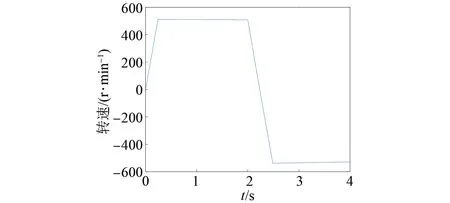
图15 模糊并联法仿真的电机转速

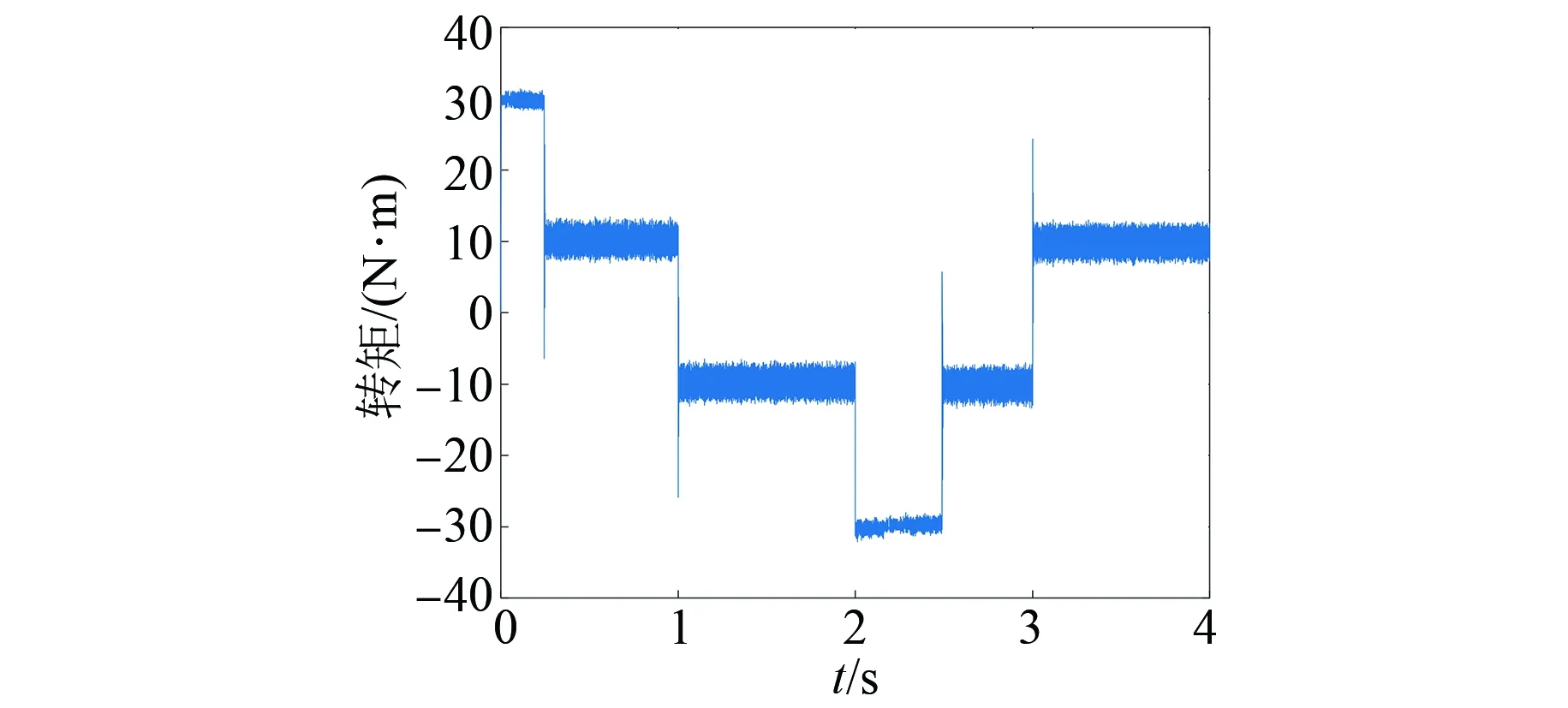
图16 模糊并联法仿真的电机转矩

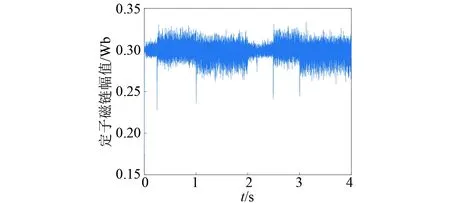
图17 模糊并联法仿真的定子磁链幅值

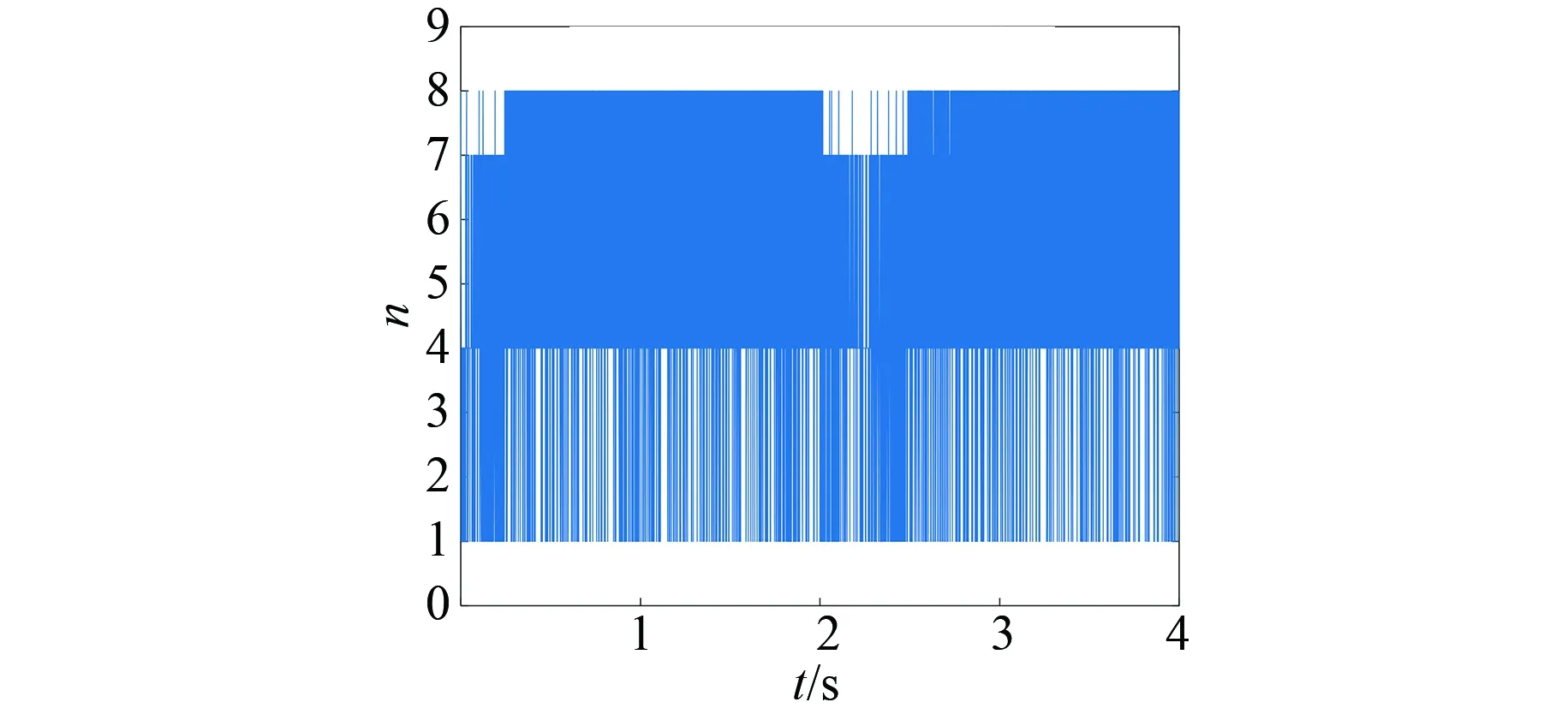
图18 模糊控制器输出n

当m=3，n=1，4，7，8和模糊调节n时，PMSM并联法MPTC系统性能如表7所示。

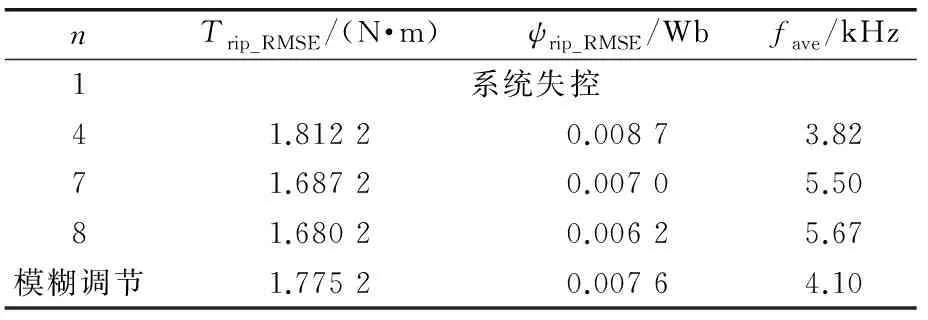
表7 模糊并联法MPTC系统性能

由仿真结果可知，模糊控制可根据转矩和磁链误差，动态调节开关次数电压矢量集合个数，在误差较大时，n较大，侧重减小脉动；误差较小时，n较大，侧重减小开关频率。和m=3、n=4相比，模糊控制性能较好，且可以减小定子磁链误差峰值，开关频率略有增大；与m=3、n=7和8相比，转矩和磁链脉动有所增大，开关频率较小。与权重系数等于0.005的传统MPTC相比，转矩、磁链脉动及开关频率均有所降低。

5 结 语

(1) PMSM并联法MPTC将多目标成本函数加权求和转换为单目标成本函数电压矢量集合求交集，从而消除权重系数。

(2) 对于并联法，增大某一控制目标集合的电压矢量个数，则弱化对该控制目标的控制，该目标的控制性能变差。

(3) 通过模糊控制动态调整控制目标集合的电压矢量个数，可根据系统实时运行状态，优化系统控制性能。相对于连续变化的权重系数，由于电压矢量个数离散有限，模糊控制器设计简单易行。