一种铁路机车信号时域检测方法的验证与思考
黄斌
柳州铁道职业技术学院 广西柳州 545616
机车信号又被称为机车自动信号,设在机车或动车组的驾驶室内,用来有效自动地反映铁路列车运行前方地面信号机的显示状态,从而辅助司机安全驾驶列车。我国的铁路干线主要采用了ZPW-2000A型无绝缘移频自动闭塞系统,该系统中ZPW-2000A无绝缘轨道电路作为铁路运输信号基础安全设备,已经被确立为今后铁路发展的统一制式。
机车信号系统中,机车信号接收器从钢轨上接收到ZPW-2000A轨道电路信息,对其进行解调处理,恢复出低频调制信号。为保证列车的行车安全,要求机车信号检测应非常可靠,目前针对移频信号检测的研究普遍转向抗干扰能力强的频域分析法,产生了很多种算法。但这些算法由于要处理的数据多运算量大,普遍必须依靠昂贵的超大容量处理器或外接存储器来实现,严重影响了系统的效率和可靠性。而在时域算法方面,也存在多种算法,如自适应滤波法[1-2]、滤波法[3]、盲分离法[4]、自相关解调法[5]等,本文对参考文献[5]中自相关解调算法进行了实际验证,分析了该方法的优点与缺点,并且针对缺点提出了一种解决方法。
1 机车信号与算法原理
1.1 机车信号
在铁路发展史中,地面信号机一直是列车司机行车的指令,由于信号机装在铁路线的路侧,因此,司机的视线受线路曲线、隧道等影响,给瞭望前方条件带来了很大困难,在大雪、大雨、沙尘暴、大雾等较为恶劣的天气下,地面信号机的显示无法被司机看清。此外,随着列车运行速度的不断提高,特别是高速动车组的出现与运用,依靠地面信号行车已无法保证列车运行安全。如以200km/h的速度行驶的列车,当司机发现地面信号机显示红色信号时,即使立即使用紧急制动,但是列车存在巨大惯性,会冲出前方信号机,造成“冒进”。因此,高速列车单纯依赖地面信号机来行车已不再安全。为了解决这个问题,研制出了机车信号机,它被装在机车司机室内,用于把地面信号“搬移”到车上,显示同地面信号机显示意义一致的信号,司机在行车过程中以机车信号机显示为主,以地面信号机显示为辅,从而保证了行车安全,提高了运行效率,也改善了司机的工作条件。
机车信号如何把地面信号“搬移”到列车上呢?首先,轨道电路采用ZPW-2000A移频轨道电路,轨道电路中有地面信号机显示的对应低频信息,如地面信号机显示红灯,此时本区段轨道电路移频信息中的低频信息为26.8Hz,显示意义为“禁止列车越过前方信号机”。其次,钢轨上部、列车底部安装有轨道电路接收天线,当列车在线路上运行时,接收天线从钢轨中接收移频轨道信息,送往信息处理模块。最后,通过信息处理模块解调后,根据低频信息来控制机车信号机显示相应灯光,如果接收到26.8Hz的低频信息,则机车信号机显示半红半黄的灯光,表示禁止列车越过前方地面信号机,与地面信号机显示红灯意义一致,从而实现信号显示的“搬移”。
1.2 时域算法原理
ZPW-2000A移频轨道信号采用相位连续的移频键控(frequency-shift keying,简称FSK)信号[6]。即通过频率调制的方法,把低频调制信号搬移到较高频率(载频f0)上,以形成振幅不变、频率随低频信号的幅度作周期性变化的调频信号。设键控信号为低频调制信号f(t),周期为T,时间表示式为:
(1)
其中A为方波的振幅,低频调制信号输出低电位时,载频f0向下偏移Δf(称为频偏),为f0-Δf即fl,叫作下边频;当低频调制信号输出高电位时,载频f0向上偏移Δf,为f0+Δf即fh,叫作上边频。移频信号受低频信号的调制而进行下边频和上边频交替变化,两者在频率切换处相位连续并且单位时间内变化的次数与低频调制信号的频率相同[7]。
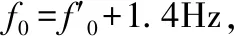
f(t)=Acos[ω0t+g(t)]
(2)
其中:
式中,Δω=2πf为移频信号的频率偏移量。波形如图1所示。

图1 机车移频信号波形
根据参考文献[5]知道,移频信号用余弦信号表示为x(t)=cos(ω0t),将原信号与延时τ后的信号进行相乘,如下:
x(t)·x(t-τ)=cos(ω0t)·cos[ω0(t-τ)]
(3)
式中B=cos(ω0τ)/2,可见B与移频信号的频率和延时τ有关,在频率不变时,B不变,如fh=1712.4Hz,ω0=2πfhτ。本文通过实验找出最佳的B值。
2 算法验证与分析
2.1 验证环境
机车信号来自实际ZPW-2000A发送器输出信号,引到铁路沙盘轨面上,形成4个区段,每个区段接收端有短路电阻,在轨面上方10cm处悬挂接收线圈,模拟机车从轨道上感应移频轨道信息,形成机车信号信息。感应到的轨道电路信号通过低频滤波、幅度放大、电压采样并送给处理器处理。
根据奈奎斯特定律,当采样频率低于2倍频谱峰值时,会出现频谱混淆现象。当采样频率超过2倍时,其频谱不会出现混淆。奈氏标准的另一种表示方式是:理想的低通信元每秒传送两个符号。如果符号的传送速度超出奈氏标准规定的范围,符号间会发生相互干扰,导致接收方不能准确地判断符号。
对机车信号采集时,为减少采集带来的干扰且保证信号幅度的准确性,一般采集频率是被采集信号最高频率的2.5倍以上,在ZPW-2000A中最高频率大于2600Hz,所以采样频率应大于6500Hz,一方面保证采集幅度的准确性,另一方面保证频率误差尽量小,这里最终的采样频率为12800Hz。验证环境如下:
(1)真实移频轨道信号,在开路情况下,轨面电压2.0V。
(2)轨面上方10cm安装空芯方形感应线圈,内径22mm×39mm,线径0.15mm,电感量180mH,内阻283Ω,厚度5mm。
(3)利用感应线圈接收到移频轨道信号作为机车信号,然后对机车信号放大50倍后,输入处理器的信号的峰峰值大约3.0V。
(4)处理器采用STM32F4高性能单片机,时钟168MHz;采样频率12800Hz。
2.2 STM32F4单片机
STM32F4单片机的内核为Contex-M4,最高频率168MHz,并拥有FPU单元,有利于浮点数据运算。Contex-M4有数据总线、指令总线、系统总线,三条总线通过总线矩阵与片上的各种资源和外设连接。
AHB1总线上的最高频率为168MHz,每组GPIO端口连接在AHB1总线上,8个16位端口和1个12位端口,为单片机输入输出提供高速通道。
AHB1总线分出两条外设总线,分别为APB1总线和APB2总线。APB2是高速外设总线,其最高频率84MHz,主要外设有EXTI、TIM1、TIM8~TIM11、USART1、USART6、SPI1和3个ADC。
2.3 采集验证
由前述可知,机车信号中的低频信息最低为10.3Hz,为能采集出完整的一个周期的10.3Hz信号,考虑到采集开始点为随机,预留半个周期,因此至少采集最小低频10.3Hz的1.5个周期。设采集点为N,则
(4)
考虑到处理过程中数据的移位等,这里采集点N取2149点。数据通过串口输出,由Excel生成图形展示。先以载频为1700-1系(1701.4Hz)、低频为10.3Hz为例,图2为2149点采集数据。
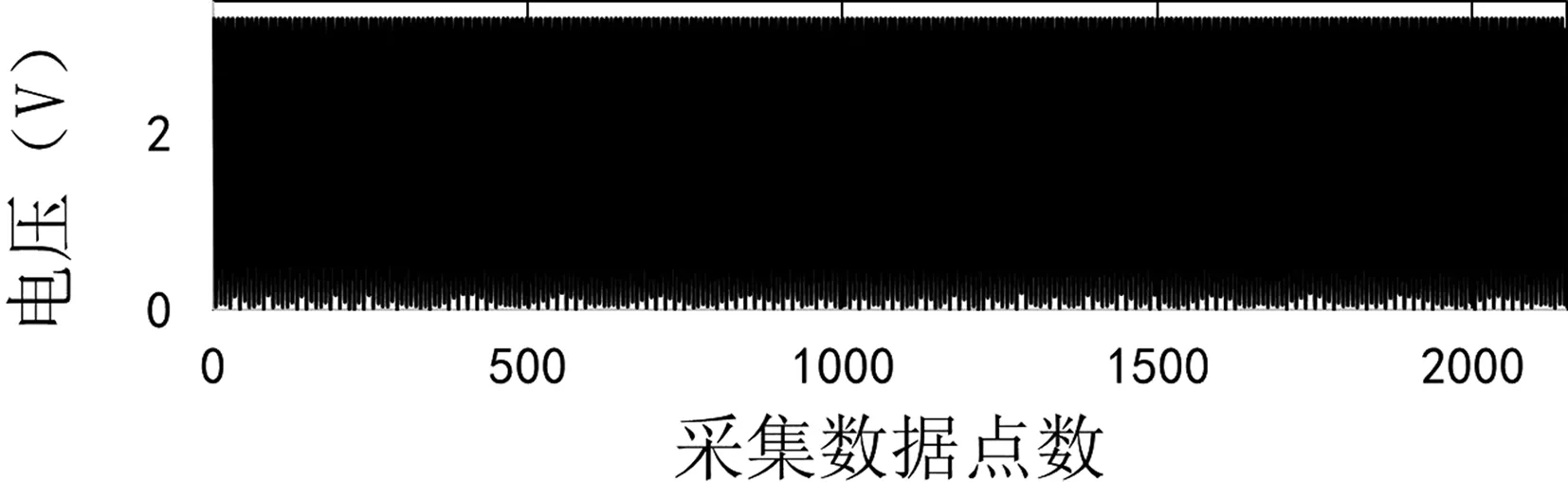
图2 1700-1系载频,低频为10.3Hz的采集信号
数据移位通过多次实验,移位数据尽量小,在此采样频率下τ=149时效果最好,该数值对四种载频的-1系、-2系均可。两组数据进行相乘,由于移位149个点,输出数据点为2000。移位处理函数程序如下:
void scox(float *xn,int time,int lenth)
{ int i;
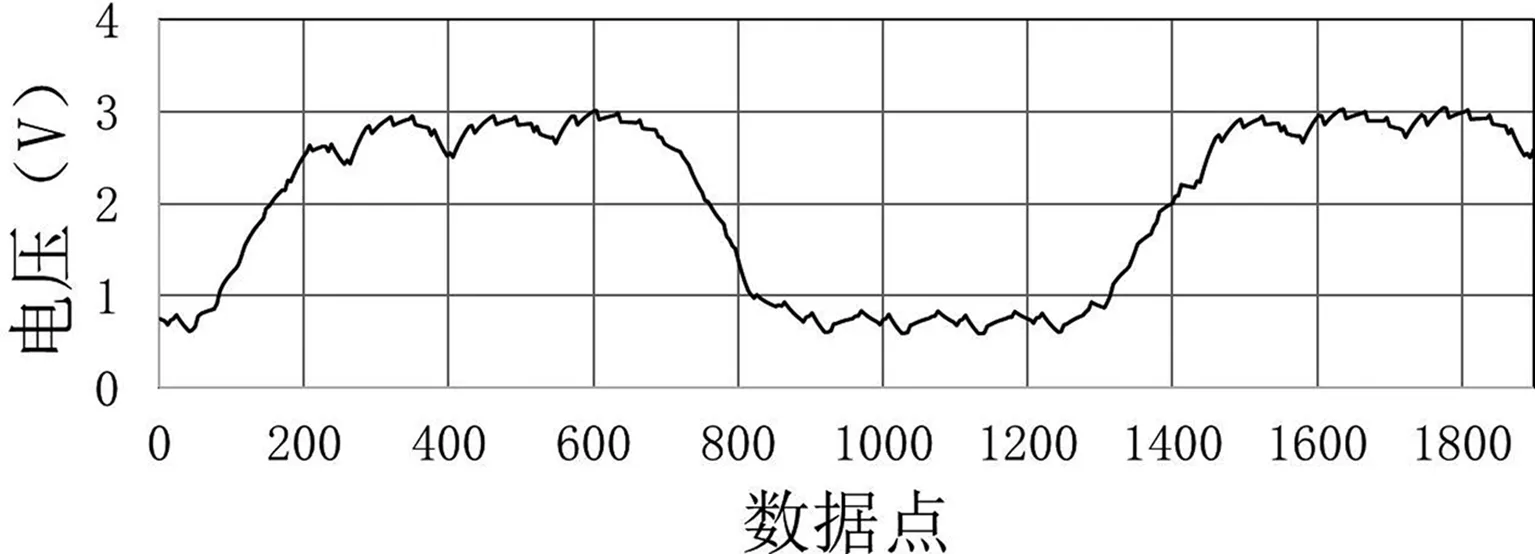
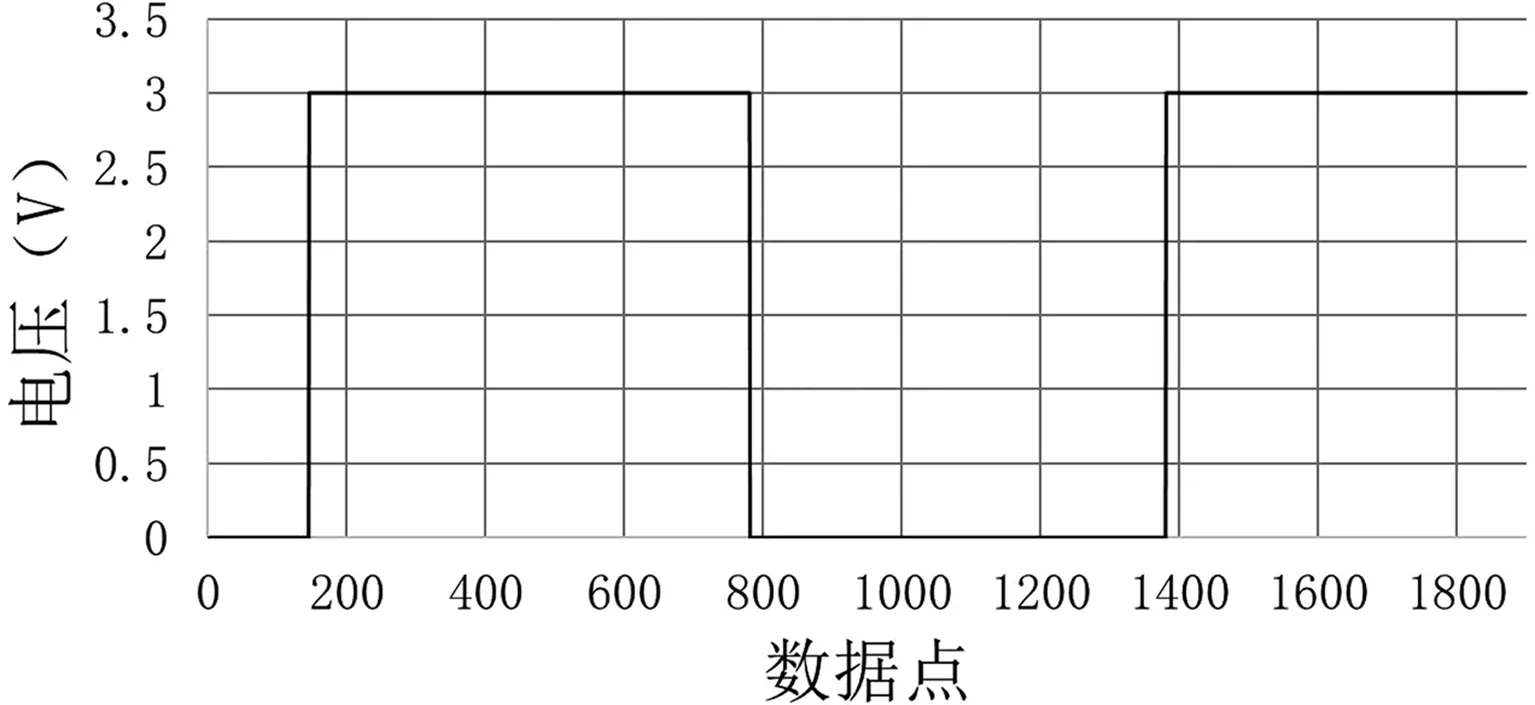
for(i=0;i { xn[i]=xn[i]*xn[i+time];} } 函数中xn为输入信号,time为数据移位数,这里time=149,lenth为输入信号数据总长度,为2149点。波形如图3所示: 图3 两信号相乘后的自相关波形 由图3可以看出,通过自相关解调算法处理后的数据,已经形成了幅度具有低频信息包络的信号。为了使获得的包络信号比较平滑,需要进行对自相关处理后的数据进行平滑处理,平滑后的信号通过数字检波与滤波后,滤除掉高频信号,留下低频信号滤波系数取0.06。平滑程序如下: void Pinghua(float *xn,int len) { int i; for(i=0;i { if(xn[i]>xn[i+1]) {xn[i+1]=0.99*xn[i];} else{xn[i]=xn[i+1];} } } 平滑后的信号通过数字检波与滤波后,滤除掉高频信号,留下低频信号,其函数程序如下所示: void lv(float *yn,int len,float u) { int i; for(i=1;i } 函数中yn为输入信号,u为滤波系数,该系数取0.06,len为输入信号数据长度,此处为2000点。通过处理后的波形如图4所示: 图4 低频包络信号波形 低频信号经过数字施密特触发进行整形,就可以转为方波信号,其函数如下: void fangbo(float *xn,int len) { int i; float max,min,pingjun,shangp,xiap; max=xn[0];//最大值 min=xn[0];//最小值 for(i=0;i { if(max<=xn[i]) { max=xn[i];}//获取最大值 if(min>=xn[i]) { min=xn[i];}//获取最小值 } pingjun=(max+min)/2.0; shangp=pingjun+(max-min)/50.0;//上偏值 xiap=pingjun-((max-min)/50.0);//下偏值 if(xn[0]>=pingjun)//第一个数据 { xn[0]=1; }else //大于上平均值为1 { xn[0]=0; } //否则为0 for(i=1;i { if(xn[i]>shangp) { xn[i]=1; } //大于上偏值为1 else if(xn[i] { xn[i]=0; }//小于下偏值为0 else {xn[i]=xn[i-1];}//否则保持为1或者0,符合施密特触发 } } 经过处理后数据波形如图5所示: 图5 低频包络信号转为方波信号 由本例中可以看出,上升沿与下降沿坐标依次为145、781、1381,可以计算出低频为12800/(1381-145)=10.36Hz。当载频为1700-1系、低频为29Hz时,得到的方波信号如图6所示。 图6 载频为1700-1系、低频为29Hz时的方波 通过计算可得低频为29.27Hz。通过对机车信号4种载频、18种低频信息进行反复测试验证,形成了低频检测验证报表,如下表所示: 低频检测平均值与最大误差表 从上表中可以看出,18种低频中,算法的检测结果的次数越多,平均值越接近理想值,最大误差值随着低频的变大有逐渐减小的趋势,这是因为在同样采样点的情况下,低频越高,采集到的周期越多,计算的检测平均值就越接近理想值。 综合结果来看,参考文献[5]中自相关解调算法检测机车信号低频信息,在2149采样点下,可以发现单次检测结果误差较大,且误差不规律,多次检测平均结果相对较好,因此,该算法整体表现并不理想。从数据分析可以推测,如果增加采样点数,单次检测结果误差会渐渐变小,但需要增加采样点数,从而增加运算量。参考文献[5]对机车信号的载频信息检测采用FFT技术、重心法频谱校正技术以及边界判断算法,导致算法复杂,运算量大。 根据以上分析,由于机车信号频率为ZPW-2000A轨道信号,以1700Hz为例,1700-1型载频的中心频率为:f0=1701.4Hz,1700-2型载频的中心频率为:f0=1698.7Hz,1700-1型与1700-2型的中心频率相差2.7Hz,故可采用FFT算法直接求解。在采样频率为12800Hz下,采集12800个点,间隔D=25个点取一个数据,进行N=1024点FFT变换,得到进行FFT变换的频率分辨率为: (5) 如前述分析结果,在12800点数据下获得的低频信息更加精确。同时,该分辨率是可以满足要求[7-8]的。 通过对自相关解调算法的验证与分析可以发现,在采样数据较少的情况下,检测出机车信号低频信息的结果存在较大误差,但在提高采样数据的情况下,计算出的低频信息误差较小,满足技术要求。通过对所采集的数据进行间隔25点抽样,然后进行1024点FFT变换,此时FFT变换分辨率也满足技术要求,有效地克服了参考文献[5]的精度不高、运算量大、采样时间长的缺点,为机车信号的可靠检测提供参考。
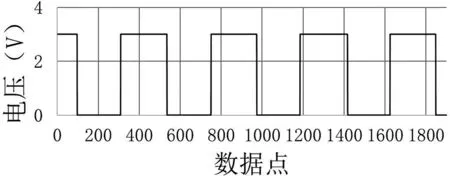
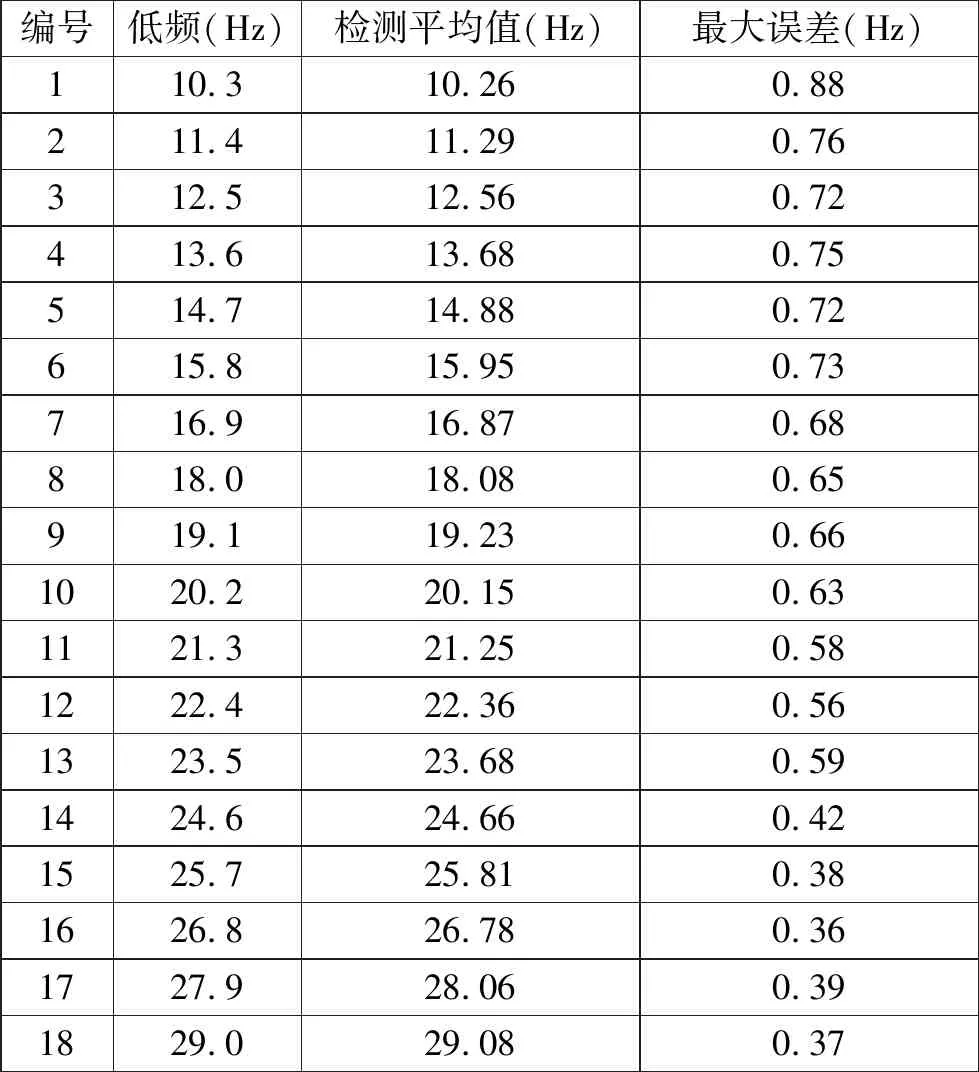
2.4 结果分析与思考
结语

