犹豫模糊数据对象集的谱聚类算法
孙爽爽,黄德才,陆亿红
(浙江工业大学 计算机科学与技术学院,杭州 310023)
1 引 言
聚类分析是数据挖掘领域的重要方法之一,也是目前研究最为活跃、内容最为丰富的领域之一.聚类通常是将一个数据对象集划分成若干个称为簇的子集[1],使得同一个簇中的数据对象之间的相似度较高,不同簇之间的对象相似度较低,这些簇有助于解析数据潜在的分布特征并为其它数据分析技术或服务奠定基础.聚类分析在帮助人们获取潜在的、有价值的信息过程中起到至关重要的作用.
传统的聚类方法大致分为基于划分聚类、层次聚类、基于密度的聚类、基于网格的聚类、基于图论的聚类等.这些针对确定性数据的聚类算法已相对成熟,并在图像分析[2,3]、模式识别[4]、知识发现[5]和生物信息学[6,7]等领域得到了广泛应用.基于图论的谱聚类算法更是受到了广泛的研究和应用,1973年Donath和Hoffman[8]首次提出谱聚类的最初模型,该模型是基于邻接矩阵特征向量的图划分方法.2000年,Shi和Malik[9]根据规范化割集准则提出了进行图分割的谱聚类算法—NCut算法.2002年,Hagen和Kahng[10]根据比例割集准则提出了进行图分割的谱聚类算法—RCut算法.谱聚类算法是基于谱图理论中图的最优划分思想提出的,其本质是把数据的聚类问题转化为寻求一种对图的最优划分的问题.理论上谱聚类算法能够对任意形状的样本空间聚类,并得到全局最优解.
随着信息时代数据量的爆发,也使得不确定性数据更为常见,如何从海量的不确定性数据中挖掘有价值的信息成为了近年来的一个研究焦点.1965年Zadeh[11]首先提出了模糊理论,用来处理不确定信息和模糊数据,其模糊性是通过一个元素属于一个集合的隶属度进行表示的,后来他又提出了采用[0,1]区间来表示一个元素属于一个集合的不确定性程度[12].Atanassov[13]提出了直觉模糊理论,直觉模糊集包含元素的隶属度,非隶属度和不确定度这3个部分.随后有不同学者提出了type-2型模糊集理论和n-型模糊集理论[14],以及多重模糊集理论[15]等适用于不同情况的模糊集理论.
2010年,Torra和Narukawa[16,17]提出了犹豫模糊集的概念,它也是模糊集理论的一种扩展,与其他模糊集理论不同的是其允许元素的隶属度在一定的区间变动,可以解决犹豫度不确定的情况.2014年,Chen[18]提出了犹豫模糊数据对象集的层次k-means聚类算法(HFHC),仅仅给出了实例说明聚类计算过程,并没有给出仿真分析结果.该算法是层次聚类算法与k-means算法的结合,把层次聚类算法的结果作为k-mean算法初始的簇中心,解决了k-means算法对初始簇中心敏感的问题,但存在对异常点敏感的问题,容易聚成链状的问题.王等[19]提出了凝聚中心犹豫度恒定的模糊层次聚类算法(FHCA),并进行了模拟数据的仿真分析.该算法根据数据本身设计了新的权重公式,提出了新的层次聚类簇中心计算方法,虽然降低了算法的时间和空间复杂度,但损失了原始数据的不确定性,且与HFHC算法存在同样的问题.张等人[20]提出了一种基于密度峰值的加权犹豫模糊数据对象集的聚类算法,降低了簇中心计算的复杂度,并提高了对不同规模以及任意形状数据集的适应性.
目前,现有的犹豫模糊数据对象集层次聚类算法受异常点影响较大且容易聚成链状,首先改进了犹豫模糊集之间相似度的计算方法,提出了一种可扩展的犹豫模糊集之间的加权相似度计算方法,该方法不仅可以利用不同的函数计算相似度,还可以根据实际问题构造最优的相似度函数.在此基础上,结合经典的谱聚类算法,提出了基于犹豫模糊数据对象集的谱聚类算法SCHF.针对目前国内外还没有可用于犹豫模糊数据对象集聚类的标准数据集的现实情况,提出了一种确定性数据的犹豫模糊方法来构造模拟的犹豫模糊数据对象集,并在仿真实验中应用.仿真实验不仅验证了SCHF算法的有效性,而且表明SCHF算法比已知的两种犹豫模糊聚类算法有更好的聚类效果.
2 相关工作
2.1 相关定义
定义1.对于定论域X,X上的犹豫模糊集A是指集合X通过函数h映射到[0,1]区间的一个子集合.Xia和Xu[21]总结给出了犹豫模糊集合(hesitant fuzzy sets,HFS)的数学表达式如下:
A={
其中的hA(x)是一个取值在[0,1]之间的集合,表示元素x∈A的不确定性程度,即元素的隶属度集合.hA(x)是犹豫模糊集A的基本单位,称其为犹豫模糊元(HFE).hA(x)有下面两个性质
1)若∀x∈X,hA(x)={0},则A=φ;
2)若∀x∈X,hA(x)={1},则A=X.
定义2.λ=|hA(xj)|为犹豫模糊元hA(xj)的犹豫度.犹豫度λ表示犹豫模糊元中的隶属度的个数.
Torra和Narukawa[16]定义了对于任意给定的两个犹豫模糊元h1,h2,并、交、补、指数、数乘运算方式.
1)h1∪h2=∪γ1∈h1,γ2∈h2{γ1,γ2};
2)h1∩h2=∪γ1∈h1,γ2∈h2{min{γ1,γ2}},|h1|=|h2|;
5)λh1=∪γ1∈h1{1-(1-γ1)λ},λ>0.
在计算两个犹豫模糊元的交集时,要求两个犹豫模糊元的犹豫度相等.需要对两个犹豫度不同的犹豫模糊元中犹豫度小的一方进行补充,在对犹豫度小的模糊元补充隶属度时并没有特定的标准,理论上0~1之间的任何数都可以.本文采用均值法,在根据隶属度决策时,隶属度的取平均值进行填充.
例1.两个给定的犹豫模糊元h1={0.3,0.5},h2={0.2,0.6,0.9},对h1进行数乘、指数和补集的运算,对h1和h2进行并集和交集的运算.
数乘:λh1=∪γ1∈h1{1-(1-γ1)k}={1-(1-0.3)k}∪{1-(1-0.5)k},若取k=2,则2h1={1-(1-0.3)2}∪{1-(1-0.5)2}={0.51,0.75}.
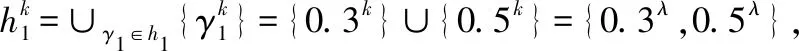
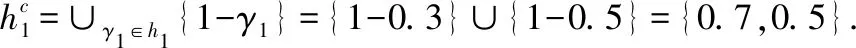
并集:h1∪h2=∪γ1∈h1,γ2∈h2{γ1,γ2}={0.3,0.5,0.2,0.6,0.9}.
交集:λ1=|h1|=2,λ2=|h2|=3,因此对h1采用均值进行补充,补充之后的h1={0.3,0.4,0.5}.
h1∩h2=∪γ1∈h1,γ2∈h2{min{γ1,γ2}}=
{min(0.3,0.2)}∪{min(0.4,0.6)}∪{min(0.5,0.9)}={0.2,0.4,0.5}
定义3.若X={x1,x2,…,xj,…,xd},其中每个分量xj都是犹豫模糊元,则称X为d维的犹豫模糊集合,简称犹豫模糊集.
定义4.若D={X1,X2,…,Xi,…,Xn},其中每个Xi都是d维犹豫模糊集,则称D为犹豫模糊数据对象集.
2.2 谱聚类算法框架
谱聚类算法是将聚类问题转化为图的最优划分问题,然后通过引入拉普拉斯矩阵,对数据进行降维表示,转化为对其向量空间的聚类,理论上可以得到全局最优解.谱聚类算法的主要步骤如下:
步骤1.根据输入的数据构造相似度矩阵S;
步骤2.根据相似度矩阵得到邻接矩阵W和度矩阵,并求出拉普拉斯矩阵L;
步骤3.计算归一化拉普拉斯矩阵的最小的k个特征向量;
步骤4.对k个特征向量进行聚类,得到聚类结果.
3 犹豫模糊数据对象集的谱聚类算法
3.1 加权犹豫模糊相似度
定义5.设A,B,C是论域X的3个犹豫模糊集,若S(A,B)满足以下4点,则称S(A,B)为犹豫模糊集A和B的加权犹豫模糊相似度:
1)S(A,B)=0,当且仅当A=φ,B=X或B=φ,A=X时;
2)S(A,B)=1,当且仅当A=B时;
3)若A⊆B⊆C,则有S(A,C)≤S(B,C),S(A,C)≤S(A,B);
4)S(A,B)=S(B,A).
定理1.设对象集D={X1,X2,…,Xi,…,Xn},对于X∈D,设X={x1,x2,…,xj,…,xd}的3个犹豫模糊集A,B,C的第j个属性对应的3个犹豫模糊元分别为hA(xj),hB(xj),hC(xj),定义S(A,B)如公式(1)所示:
(1)
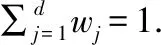
f:[-1,1]→[0,1]表示f是集合[-1,1]到集合[0,1]的一个映射函数.f(x)满足:
1)对称性,∀x∈[-1,1],f(x)=f(-x);
2)单调性,f(x)在[-1,0]上单调递减,在[0,1]上单调递增,且f(0)=0,f(1)=1.
g:[0,1]→[0,1]表示g是集合[0,1]到集合[0,1]的一个映射函数,g(x)满足在[0, 1]上单调递增, 且g(0)=0,
g(1)=1.
那么S(A,B)称为犹豫模糊集A和B的加权相似度.
证明:
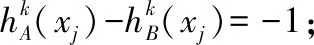
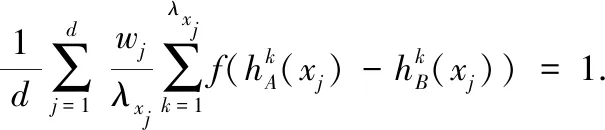
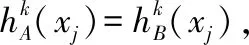
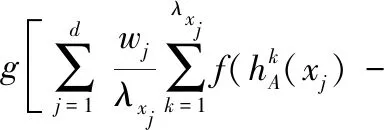
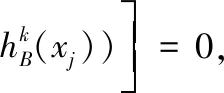
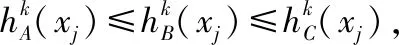
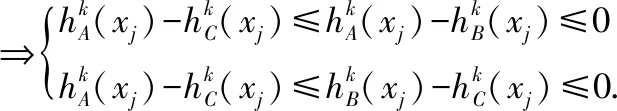
由f(x)在[-1,0]单调递减,可得出:
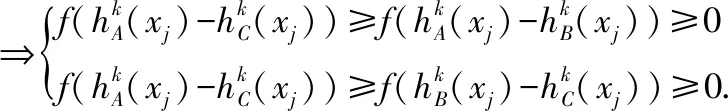
由g(x)在[0,1]上单调递增,可得:
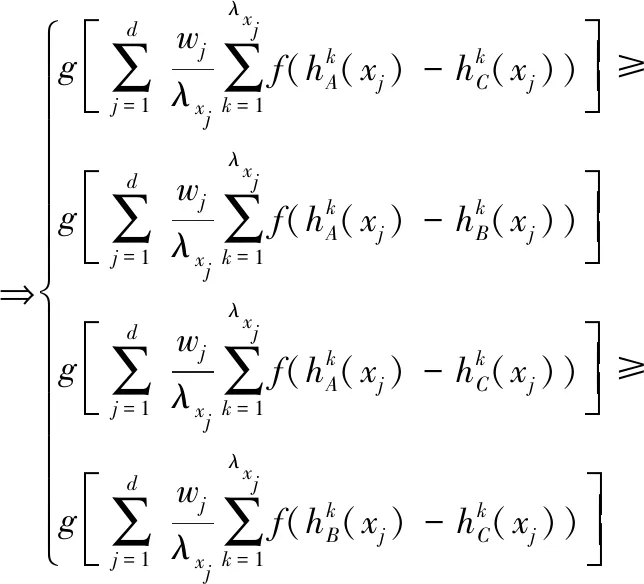
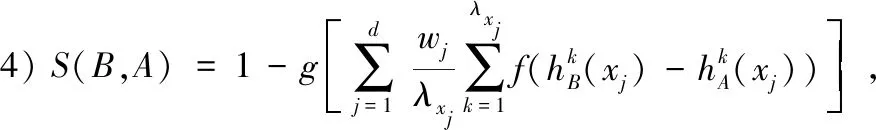
当选择满足以下条件的函数f和函数g时,可以得到不同的加权相似度函数,也可以根据实际问题构造加权相似度函数.
f:[-1,1]→[0,1]表示f是集合[-1,1]到集合[0,1]的一个映射函数.f(x)满足:
1)对称性,∀x∈[-1,1],f(x)=f(-x);
2)单调性,f(x)在[-1,0]上单调递减,f(x)在[0,1]上单调递增,且f(0)=0,f(1)=1.
g:[0,1]→[0,1],表示g是集合[0,1]到集合[0,1]的一个映射函数,g(x)满足在[0,1]上单调递增,且g(0)=0,g(1)=1.
取f(x)=|x|,取g(x)=x.将其带入公式(1)得到绝对值加权相似度S(A,B),如公式(2)所示,1-S(A,B)可得文献[19]中的加权距离公式.
(2)
进行一般性的推广,令f(|x|)=|x|p,g(x)=xq,p∈R+,q∈R+,此时f(x)与g(x)均满足条件.得到A和B的加权犹豫模糊相似度公式,如公式(3)所示,指数曲线f(x)与g(x)如图1所示.由于f(x)=f(-x),为了方便,只展示0-1部分.
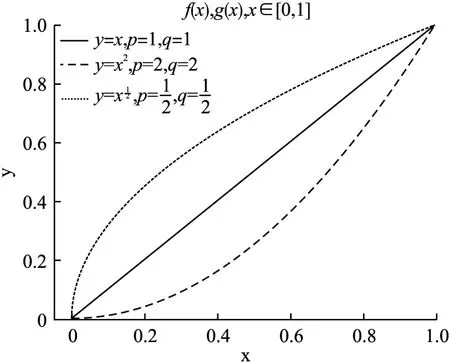
图1 f(x)与g(x)的指数曲线Fig.1 Exponential curve of f(x)and g(x)
(3)
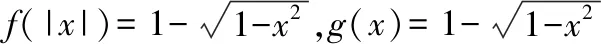
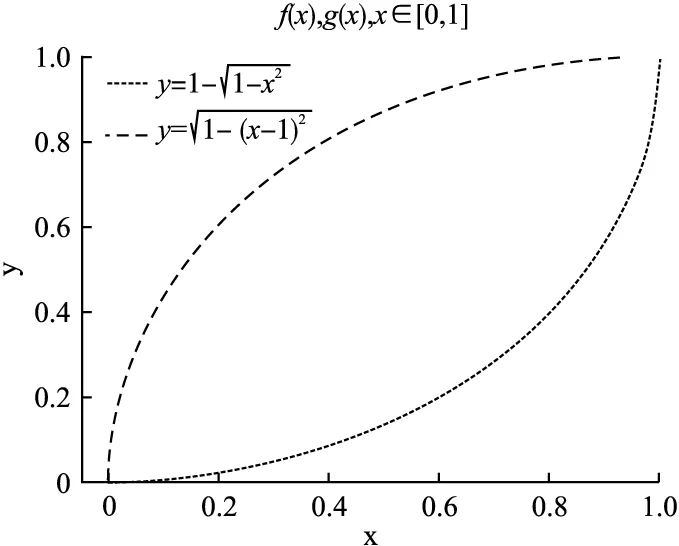
图2 f(x)与g(x)的球形曲线Fig.2 Spherical curve of f(x)and g(x)
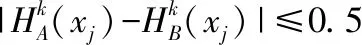
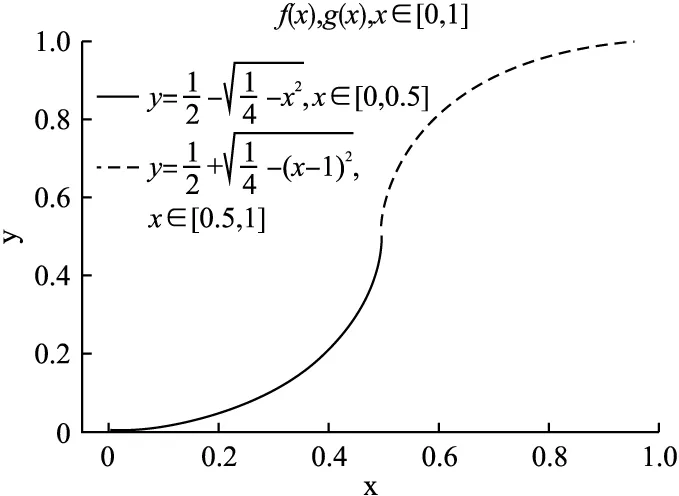
图3 f(x)与g(x)的S形曲线Fig.3 S-shaped curve of f(x)and g(x)
(4)
(5)
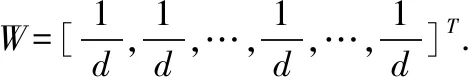
(6)
(7)
定义6.设犹豫模糊对象集D={X1,X2,…,Xi,…,Xn},Xi∈D都是d维犹豫模糊集,称MSnxn为犹豫模糊对象集的加权相似度矩阵.对任意D中任意两个犹豫模糊集有Xi,Xj∈D,MSij=S(Xi,Xj),i,j∈(1,2,…,n).对于MS有一下两个性质:
1)MSii=1,i=n;
2)MS是一个对称矩阵.
在谱聚类算法中,需要根据相似度矩阵MS构造对应邻接矩阵W,目前方法有σ阈值法、互为k近邻法、k近邻法和全连接法[22]等.
1)σ阈值法:当MS中任意两个犹豫模糊集的相似度大于σ时,两个犹豫模糊集之间的wij即为该边的相似度,否则,该犹豫模糊集之间的相似度为0,计算方法如公式(8)所示:
(8)
2)互为k近邻方法:利用KNN算法遍历MS,取每最近的互为k近邻的k个犹豫模糊集,邻接矩阵的生成方法如公式(9)所示:
(9)
3)k近邻方法:利用KNN算法遍历MS,取每个样本最近的k个犹豫模糊集,邻接矩阵的生成方法如公式(10)所示:
(10)
4)全连接:全连接常通过的是高斯核进行转换,得到所有的犹豫模糊集的wij都不为0,邻接矩阵的生成方法如公式(11)所示:
(11)
3.2 犹豫模糊谱聚类算法
设犹豫模糊数据对象集D={X1,X2,…,Xi,…,Xn},对于X∈D,X={x1,x2,…,xj,…,xd}.犹豫模糊数据对象集的谱聚类算法(Spectral clustering algorithm for hesitating fuzzy data object set,SCHF)的步骤如下.
输入:犹豫模糊数据对象集D,邻接数k1,降维后的维度k2,簇的数目C
输出:C个簇的聚类结果
SCHF算法步骤如下:
步骤1.由公式(7)计算权值向量W,由公式(4)、公式(5)和公式(1)计算D中任意两个犹豫模糊集的加权相似度,得到相似度矩阵MSnxn;
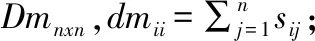
步骤3.计算拉普拉斯矩阵Lnxn,L=Dm-MS;
步骤4.计算拉普拉斯矩阵L进行特征分解,得到的前k2小的特征值对应的特征向量,组成特征向量矩阵Vnxk2,其中矩阵中的每一行是一个犹豫模糊集在k2维空间中的表示;
步骤5.使用k-means对Vnxk2进行聚类,得到C个簇的聚类结果.
3.3 确定性数据的犹豫模糊化方法
目前国内外没有可用于聚类的标准化犹豫模糊数据集,因此提出了一种确定性数据的犹豫模糊化方法(Hesitant fuzzification of deterministic data,HFD)构建模拟的实验仿真数据.
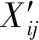
maxj=max(X1j,X2j,…,Xij,…,Xnj)
(12)
minj=min(X1j,X2j,…,Xij,…,Xnj)
(13)
(14)
输入:确定性数据集D,犹豫度λ
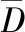
步骤1.对数据集D根据公式(14)进行归一化,得D′;
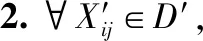
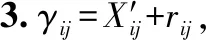
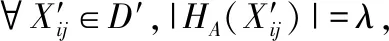
从确定性数据犹豫模糊化方法步骤可以得出,HFD只对数据集本身进行犹豫模糊化,并不会对原来数据属于某个簇做出改变,犹豫模糊化后的数据集与未模糊化集簇的属性一致.
4 实验与分析
4.1 实例验证
下面通过由8个犹豫模糊集组成的犹豫模糊对象集,验证犹豫模糊谱聚类(SCHF)的有效性,犹豫模糊集属性维度为3,数据本身为2个簇.数据如表1所示.
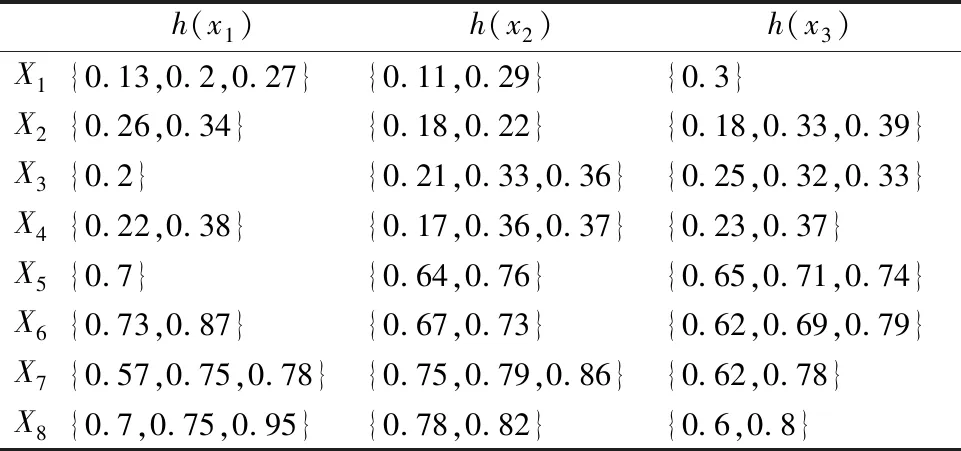
表1 犹豫模糊对象集Table 1 Hesitant fuzzy object set
首先计算权值W,通过公式(7)计算得到权值向量W=[0.334 0.354 0.312]T.通过公式(4)、公式(5)和公式(1)计算得到S形加权相似度矩阵MS1.
为了对比S曲线得到相似度矩阵与绝对值曲线相似度矩阵的效果,给出了f(x)=|x|,g(x)=x计算得到的相似度矩阵MS2,与上面的S曲线相似度矩阵对比后,可以看出上面S曲线得到的相似度矩阵起到了放缩的作用,在绝对值矩阵中值大于0.5的进行了放大,小于0.5的进行了缩小.
取k1=4,S曲线相似度矩阵MS1经过计算得到的邻接矩阵W.
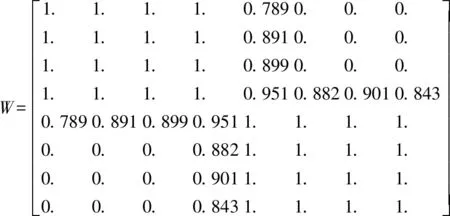
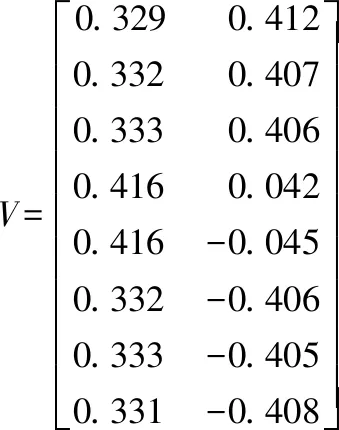
取k2=2,根据邻接矩阵W计算度矩阵Dm,然后计算拉普拉斯矩阵L,对L特征分解得到前k2小的特征向量矩阵V.其中每一行是一个犹豫模糊集在二维空间的表示.
最后特征向量矩阵经过k-means聚类,得到两个簇{X1,X2,X3,X4},{X5,X6,X7,X8}.
4.2 仿真实验
为了验证算法SCHF的聚类效果,选择了4个常用的合成数据集进行实验,数据集信息如表2所示,数据分布如图4所示.分别取犹豫度λ=2、λ=4和λ=8通过算法HFD进行犹豫模糊化.SCHF算法中近邻数k1取4,谱聚类算法中一般降维后的维度与簇数相等,所以取k2等于输入簇的数目.这里采用常用的准确率ACC、调整互信息AMI和调整兰德里系数ARI指标对聚类结果进行评估,其中ACC值的范围为[0,1],ARI和AMI 值的范围为[-1,1],它们都是值越大表示聚类效果越好.并对结果进行比较,结果如表3所示.
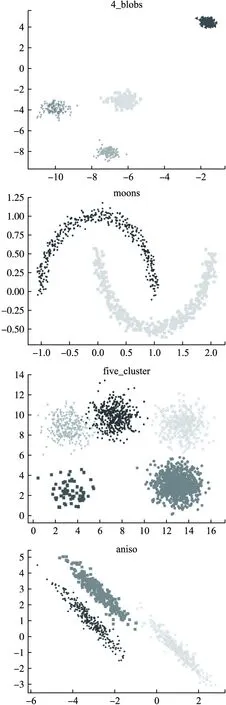
图4 可视化数据集Fig.4 Visualized data set
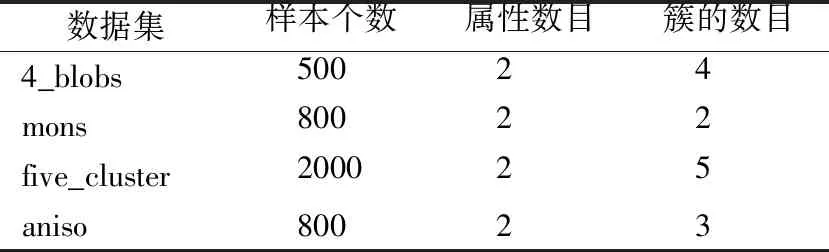
表2 数据集Table 2 Data sets
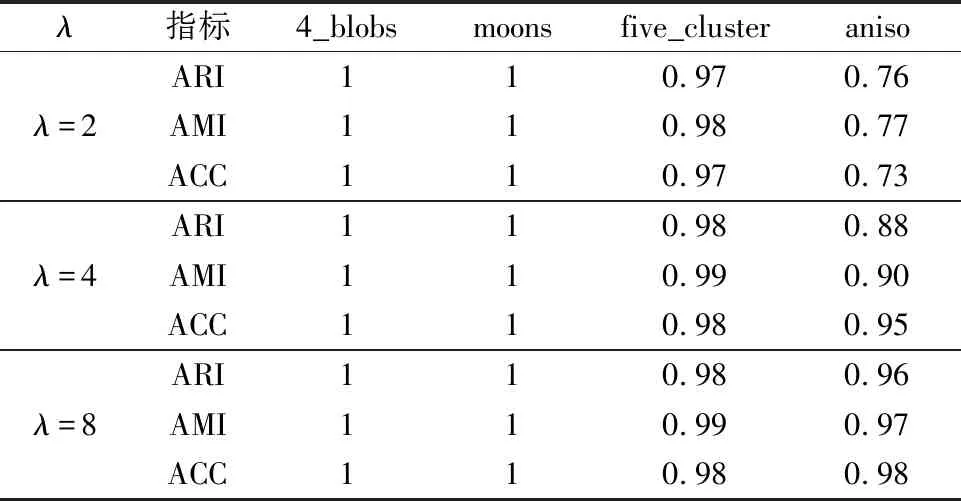
表3 SCHF聚类结果Table 3 Clustering results of SCHF algorithm
从仿真实验结果可以看出,SCHF算法对确定性数据犹豫模糊化后的聚类结果基本达到90%以上的准确率.从数据集4_blobs和five_cluster来看,SCHF对球形数据能够得到很好的聚类效果,从moons数据集来看对流形数据也得到了很好的聚类效果.从数据集five_cluster和anisol来看,随着犹豫度的增加,而增加了确定性数据的不确定程度,聚类效果没有下降反而有所提升.
对文献[18]的算法HFHC和文献[19]的算法FHCA进行对比验证.为了增加算法比较的公平性,各个算法在每个数据集上进行20次实验,取平均值,以调整兰德里系数ARI作为评价指标.表4是犹豫度为4的实验结果,表5是犹豫度为8的实验结果.
从表4和表5,可以看出算法SCHF整体优于算法HFHC和FHCA.而算法HFHC和FHCA对数据集moons和aniso的准确性较低, 因为算法HFHC和FHCA都是基于层次算法的犹豫模糊数据对象集的聚类算法,而层次算法本身受异常点影响较大且容易聚成链状,因而对模拟的犹豫模糊数据对象集moons和aniso的聚类效果较差.SCHF算法的相似度计算方法有一定的缩放作用,而谱聚类算法理论上能够对任意形状的簇得到理论上的最优解,实验对比结果体现了本文提出的可扩展加权相似度计算方法基础上SCHF算法的优势.仿真实验表明,本文算法SCHF整体优于算法HFHC和FHCA,通过实验的对比验证了SCHF的有效性和准确率.
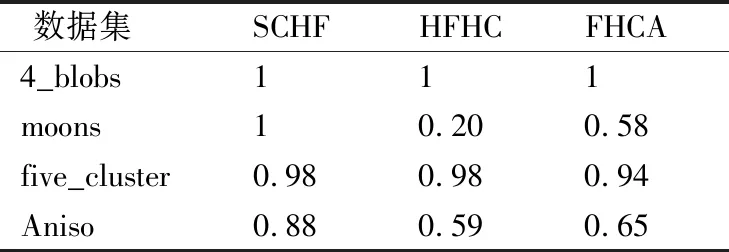
表4 λ=4各算法的ARITable 4 ARI of different algorithms
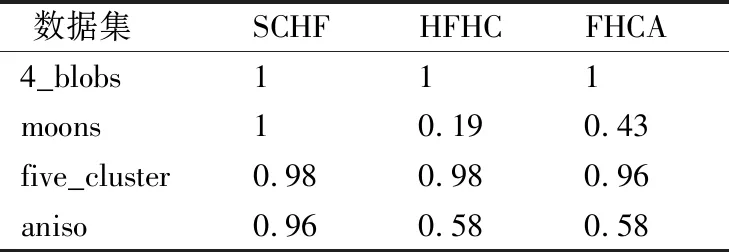
表5 λ=8各算法的ARITable 5 ARI of different algorithms
5 结束语
本文针对犹豫模糊数据对象集层次聚类算法受异常点影响较大且容易聚成链状的问题,首先提出了犹豫模糊集之间可扩展的加权相似度计算方法,在此基础上提出了犹豫模糊数据对象集的谱聚类算法SCHF,通过仿真实验验证了算法的有效性和准确率.下一步的研究方向是在犹豫模糊集加权相似度的基础上结合其他聚类算法对犹豫模糊数据对象集的聚类进行研究,并在真实环境下的犹豫模糊数据对象集上进行实验验证.

