浅谈动点轨迹之隐圆问题

张晓会

(广东省中山市第一中学 528400)

下面以近两年的中考题为例，浅谈动点轨迹的隐圆问题.

1 紧扣定义，直接作圆

例1(2020广东)有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图1，∠ABC=90°，点M，N分别在射线BA，BC上，MN长度始终保持不变，MN=4，E为MN的中点，点D到BA，BC的距离分别为4和2．在此滑动过程中，猫与老鼠的距离DE的最小值为____．

图1 图2

变式练习1例1中条件不变，求点E的运动路径的长度.

2 定弦定角，勾勒定圆

例2(2021广东)在△ABC中，∠ABC=90°，AB=2，BC=3，点D为平面上一个动点，∠ADB=45°，则线段CD长度的最小值为____.

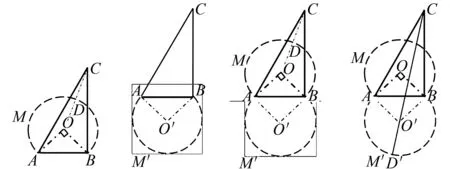
图3 图4 图5 图6

变式练习2 例2中条件不变，求线段CD长度的最大值为____.

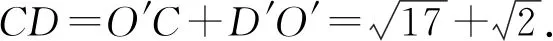
变式练习3 已知点E在等边ΔABC内部运动，∠AEB=150°，若AB=1，则点E的运动路径长度为____.

图7 图8 图9

变式练习4 已知AB=3，C为平面内一点，且满足∠ACB=120°，则点C到AB的最大距离为____.

知识拓展由特殊到一般，可将变式练习4中的条件放宽为：已知线段AB=a,动点P为平面内一点，满足∠APB=α，则可构造出P点运动轨迹所在的圆弧(记圆心为O)，圆心O在AB的垂直平分线上， 圆心角∠AOB=2α(比如，α=90°时如图10；α=45°时如图5；α=150°时如图7)，然后可求出点P的运动轨迹长度，以及相应线段的最值问题.不难发现：当α为直角时，动点P的运动轨迹是一个圆(如图10)；当α为锐角时，动点P的运动轨迹是两段对称的优弧(如图11)；当α为钝角时，动点P的运动轨迹是两段对称的劣弧(如图12).

图10 图11 图12

3 活用对角，呈现共圆

例3如图13所示，△ABC中，AH是高，AT是角平分线，且TD⊥AB，垂足为点D，TE⊥AC，垂足为点E.求证：∠AHD=∠AHE.

图13 图14

解析由已知结合四边形内角和可得∠BAC+∠DTE=180°，即有四边形ADTE对角互补，所以A,D,T,E四点共圆，且AT是直径，进而得出H也在此圆上，如图14，原问题即转化为证两个圆周角相等.

图15 图16

4 定长等角，巧用隐圆

例4如图17，在△ABC中，AB=AC，任意延长CA到点P，再延长AB到点Q，使AP=BQ，求证：△ABC的外心O与A、P、Q四点共圆.

图17 图18

解析由已知可得PC=AQ，如图18，连接OA，OC,OP,OQ,有OA=OC，所以∠OCA=∠OAC=∠QAO,进而可证△OCP≌△OAQ，所以∠CPO=∠AQO，而∠CPO与∠AQO均为固定线段AO所对的角，所以O与A、P、Q四点共圆.

变式练习6 如图19，点O是△ABC的外心，∠BAC=60°，BD和CE是△ABC的高且交于点H，在BD上截取BM=CH.(1)求证：∠BOC=∠BHC；(2)求证：△BOM≌△COH.

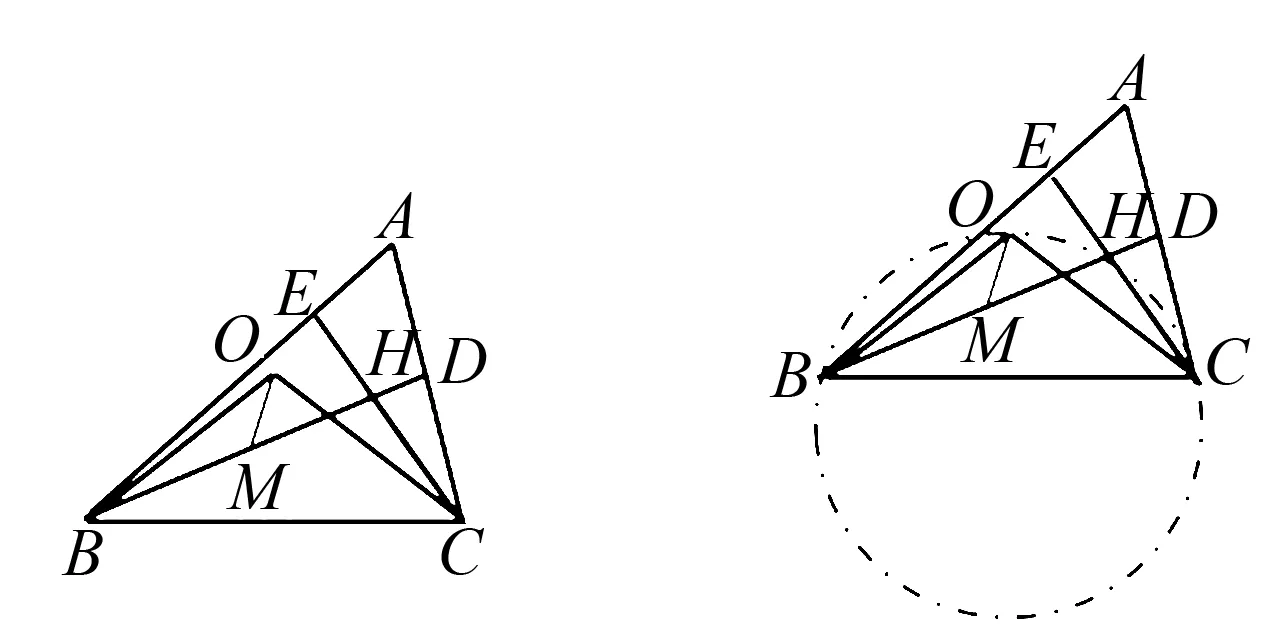
图19 图20

解析(1)由圆的性质有∠BOC=2∠BAC=120°，由四边形内角和有 ∠BHC=∠EHD=360°-∠AEC-∠ADB-∠BAC=120°，所以∠BOC=∠BHC.

(2)类似于例4，∠BOC与∠BHC均为固定线段BC所对的角，且∠BOC=∠BHC，所以B、C、H、O四点共圆(如图20)，因此∠OBH=∠OCH，所以△BOM≌△COH(SAS).

5 抽丝剥茧，回归根本

与动点隐圆轨迹相关的证明题还有很多，也有不少题目的解题方法比较巧妙，这里不一一列举.通过以上几个中考题以及变式的分析，不难发现动点轨迹的隐圆问题，从本质上来讲，就是对与圆的定义以及相关性质的灵活运用，可以将其归纳为四类：(1)从定义出发，定点、定长得定圆弧；(2)从弦与圆心角、圆周角性质出发：定弦定角得定圆弧；(3)四边形内对角分别互补，则该四边形的四个顶点共圆；(4)同一固定线段所对的角相等，则该线段两个端点和其所对等角的顶点共圆.

动点对学生的综合能力要求比较高，题目中 “不动”的条件尤为重要，需要学生以此为出发点，快速地在自己的知识体系中检索出与之相关的知识点，进行发散思维，并快速推导出相应结论.所以在平时教学中，教师要有意识地引导学生加深对课本定义以及性质的理解，要注重知识的生成过程，强化学生对于性质、定理的灵活运用，并在学生熟练掌握的基础上，培养学生发散性思维和基本的构图能力.