追求“原理一致性”的乘法分配律教学思考与实践

杨海荣

【摘   要】在“运算定律”教学中存在“学生简算技能熟练而简算意识淡薄”的问题。以“乘法分配律”的教学为例，通过“对过往教学的反思”和“对数学原理一致性的分析”，构建乘法分配律“原理一致性”的结构关联路线，将乘法分配律置于“数与运算”主题的大结构中进行整体考量、整体设计与推进教学，引导学生在结构关联中体验与感悟乘法分配律的本质，从而达成对“数与运算”主题原理一致性的深刻理解。

【关键词】原理一致性；乘法分配律；结构关联

《义务教育数学课程标准（2022年版）》（以下简称《2022年版课标》）注重内容主题的结构化整合，倡导在“把握学习内容整体性”的前提下，引导学生理解“数学原理的一致性”，促进学生核心素养的落地。《2022年版课标》对“运算能力”作了明确的内涵界定：运算能力主要是指根据法则和运算律进行正确运算的能力。主要表现为：（1）能够明晰运算的对象和意义，理解算法与算理之间的关系；（2）能够理解运算的问题，选择合理简洁的运算策略解决问题；（3）能够通过运算促进数学推理能力的发展。

就学习内容而言，“数与运算”主题的基本原理及其结构，亦规定了算理的刚性（即原理一致性），且允许算法有弹性（即算法多样化与合理简洁）。算理刚性与算法弹性体现了数学学科特质，也符合人类追求简洁的天性。如果不能深刻地理解原理的一致性，那么算法多樣化的追求就会失去依托，灵活、合理、简洁的运算追求也会缺少逻辑前提。

长期以来，“数与运算”主题的教学虽然强调“在理解算理的基础上掌握算法”，但各内容板块间的算理解释始终处于各自为政的孤立状态，缺乏原理一致性的本质关联。特别是运算定律，教师通常将其作为独立的内容进行教学，缺少与其他运算内容的关联，造成普遍的“学生简便计算的技能熟练，而主动应用运算定律进行简便计算的意识淡薄”的现状。笔者自2016年开始专注于单元整体教学的实践与研究，试图以“原理一致性的追求”对现状作出改变。本文以“乘法分配律”的教学为例，简要介绍相关思考与做法。

一、对过往教学的反思

伴随课程改革的进程，乘法分配律的教学也经历了不断变化与发展的过程。该过程基本呈现了两种主要的教学事实：一是指向知识与技能的落实；二是侧重于概念的理解。具体流程大致如下。

教学事实一：指向知识与技能的落实

1.初步感知：通过计算，引导学生发现规律。

教师呈现算式：5×（4+3）、5×4+5×3。

发现：两式结果相等，可用等号连接。5×（4+3）=5×4+5×3。

文字表述：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。

2.举例并验证：学生举例后，发现同类例子有无数个。

3.归纳模型：请学生用一个式子表示所有例子。

字母表达式：（a+b）c=a×c+b×c

4.结论：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。这叫作乘法分配律。

5.练习：匹配相应的技能训练。

教学事实二：侧重于概念的理解

1.解决问题：要求用不同的方法解决。

教师出示情境，如购物：铅笔每支5元，小明买4支，小红买3支。两人一共花了多少元？

学生给出2种方法：

方法1：5×（4+3）=5×7=35（元）。方法2：5×4+5×3=20+15=35（元）。

发现：结果相等，可用等号连接。5×（4+3）=5×4+5×3。

文字表述：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。

2.理解内涵：为什么结果相等？

结合情境解释：可以先算铅笔支数，再算钱数；也可以先分别算小明和小红的钱数，再相加。算的都是7支铅笔的钱数，所以结果相等。

用乘法意义解释：5×（4+3）表示7个5是多少；5×4+5×3表示4个5加3个5，也是7个5。意义相同，所以结果相等。

结合图式辅助理解。

3.结论：因为意义相同，所以结果相等。

4.练习与应用：匹配相应的技能训练和解决简单实际问题。

显然，两者相比较，“教学事实二”中的教学更符合乘法分配律的本质，但因区域和教师个人差异等事实，这两种方式目前还普遍并存于课堂教学之中。

针对这种教学事实，笔者对采用“教学事实二”进行教学的班级，在学生学习一个月后进行后测。基本情况如下。

后测试题：请计算下列各题。

36×34＋36×66   （4＋8）×25

学生解答典型作品：如36×34＋36×66=1224＋2376=3600；（4＋8）×25=12×25=300。

全班43人，仅1人主动运用乘法分配律进行简便计算，占比2.3%。

教师访谈：“此题你会用运算定律进行简便计算吗？”

生：用是会用的，只是、只是……（支吾不作答）

教师追问：既然会用，那为什么不用呢？

生：没想到。

生：题目中没有要求。

生：老师也没有要求。

生：如果有要求，我肯定就用了。

从对学生的后测与分析中得出，即使是使用“教学事实二”的教学，学生的学习效果也并不理想。主要表现为：学生简便运算的技能并不生疏，但主动应用运算律进行灵活运算的意识淡薄。有相当部分的学生运算结果正确，但没有运用运算律进行合理灵活的运算。对他们的访谈更能说明问题。

学生的问题来源于教学失当。“事实一”的教学忽视了概念内涵的理解，将乘法分配律的学习视为“公式记忆”及“技能操练”；“事实二”虽然重视概念本质的理解，但缺少与其相关联的上位概念的结构关联，以致学习陷于孤立状态。

这表明教师对乘法分配律的认识及教学呈现表层化、碎片化的特点。具体原因有三方面。

第一，就知识属性而言，教师将乘法分配律理解为“规则”，而非“法则”。规则属于人为的规定，具有主观性。法则属于自然规律，具有客观性，必须明理。很明显，乘法分配律是“法则”，如若将其视作规则，则教学实施必然以记忆与操练为主导。

第二，就学习方式而言，教师将乘法分配律定位为“上位学习”，而非“下位学习”。上位学习是指在认知结构中已经形成几个观念的基础上，学习一个更概括的、包摄性更高的命题时所发生的学习。下位学习是指当原有的观念在包摄和概括水平上高于新学习的命题（即新旧知识构成类属关系）时所发生的学习。因此，应将乘法分配律定位成“下位学习”，若反之，就可能将乘法分配律作为独立的内容展开教学，割断其与原有知识结构的联系。

第三，就教学目标定位而言，教师缺少整体把握。课时目标的定位必须置于目标结构（课程目标—主题目标—单元目标—课时目标）中整体考量，才能确保乘法分配律在“数与运算”主题中的地位，明确其承担的义务和责任，进而明晰其教学价值。

综上所述，教师的这些认知偏差，必然造成对课时目标定位的模糊不清，进而导致教学实施的失利。

二、对数学原理一致性的分析

教师对教学的追求往往“求于术而止于道”，表现为教学中忽视课程目标的长期渗透与落实，对学科的教育、教学的价值缺少最一般的理解和更上位的追求，对学科的基本结构缺少整体的把握。显然，乘法分配律学习的首要目标是理解定律内涵、灵活选择合理的算法，掌握运算技能次之。乘法分配律教学要依托学科知识结构，整体建构教学，引导学生感悟内容的整体关联和方法的持续迁移，理解运算原理一致性。

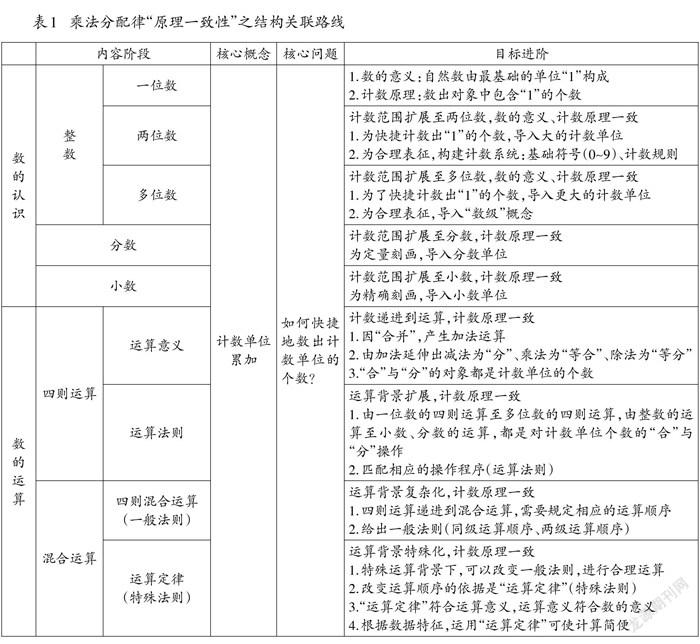
为体现“数学原理一致性”，教师需要在大尺度结构中整体考量，从不同教学内容中提炼核心概念、核心问题，确立教学目标（如表1）。

“核心概念”统摄主题内容，体现运算原理的一致性，即算法刚性。教师要引导学生明白所有内容的算理是一致的，即本质相同。“核心问题”驱动学习方式迁移，体现运算意义与价值。教师要引导学生明白运算背景变化后，算法需要作出相应改变，算法是一个不断优化计数方法的过程。在大尺度结构中整体定位目标，形成目标进阶序列。在把握“内容整体性”的基础上，理解“原理一致性”，构建起学科基本原理间的本质关联，促进学生良好思维结构的形成。

由表1的结构关联路线分析可见：“一位数的意义”是原理起点；“加法运算意义”是“数的意义”和“数的运算”原理一致性的连接点；“运算定律”是运算的特殊状态，是原理的阶段性终点。“运算定律”中“乘法分配律”的学习必定基于源头“数的意义”及整体结构的理解与把握。

三、教学对策讨论

（一）基本教学思路

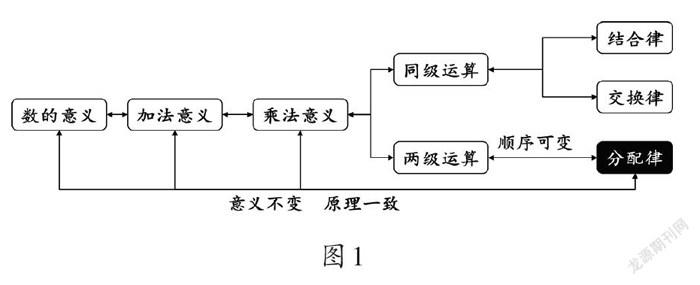
根据乘法分配律在大结构中的地位与价值，在整体结构中准确定位其目标后，可确立教学的基本思路：引导学生在整体结构中体验乘法分配律，建立概念间的本质关联（如图1）。

（二）教学需要思考的基本问题

1.乘法分配律是什么？

所谓“运算顺序”是一种混合运算的法则，可分为两个维度：一般法则与特殊法则。一般法则即同级运算与两级运算的顺序。特殊法则即运算定律。乘法分配律的表象是改变了一般法则（四则混合运算的顺序），但本质与运算的意义、数的意义相同。教学的关键在于构建与原有认知结构的本质关联，搭建特殊法则与一般法则间的通道。

2.为什么可以改变运算顺序？

改变运算顺序的前提是保证运算意义不变。教师需要让学生认识到：意义不变，则结果必然相等；意义变化，则结果必然不等。

3.乘法分配律有什么用？

运用乘法分配律一定能让运算简便吗？在具体的运算背景（运算数据）下，讨论三种状态：用与不用无所谓、用了能简便、用了反而麻烦。教师引导学生区分乘法分配律的运用背景，体验并辩证认知乘法分配律的价值，养成主动运用运算定律进行合理运算的习惯，提升数学运算能力。

（三）整体教学推进过程

教师要整体设计系列体验活动。具体课时的划分，视学生的学习起点与达成情况而定。

【教学活动1】再现原有认知结构，给出一般法则。

1.给出结构性学习材料。

①25×3+25×17  ②25×3+22×17

③25×4+25×10  ④25×（20+2）  ⑤25×（3+7）

2.请学生口述运算的顺序，教师直接呈现运算过程。

3.小结：根据一般法则，两级运算中，①②③先算乘法，④⑤先算括号内的。

【教学活动2】理解乘法分配律的内涵，建立一般法则与特殊法则间的本质关联。

1.设置挑战性大任务。能否在保证运算结果不变的前提下，改变上述①②③④⑤各题的运算顺序？并说明理由。

2.学生自主尝试计算。发现：①③④⑤改变运算顺序后，结果不变，②无法实现。整体呈现运算过程如下：

3.思辨明理。以④25×（20+2）為例，交流学生作品（如图2）。

学生作品表征形式不同，但本质相同，即都用乘法的意义解释了特殊法则与一般法则的本质关联。先乘再加：20个25与2个25的和是22个25；先加再乘：（20+2）个25，也就是22个25。意义相同，改变运算顺序后结果一定相同。

4.第①③⑤题同上。同桌之间说明理由。

5.揭示概念。给出乘法分配律的名称、文字描述及字母表达式。引导学生理解两种不同的运算顺序，只要保证运算意义相同，结果必然相等。

【教学活动3】区分运算对象（数据背景），体验乘法分配律的适用性与价值

1.对比反思，感受适用性。

师：为什么②25×3+22×17不能改变运算顺序？

生：这里一个是25×3，一个是22×17，没有共同的因数。

生：一个是3个25，一个是17个22，不能像前面一样加起来。

生：肯定要有一个相同的因数。

学生感受到，乘法分配律并不能适用于所有的运算背景，只有在特定的数据场景下才能运用，即有相同的因数，才符合乘法意义。

2.对比反思，体验价值。

教师提问：“既然用一般规则即能计算出结果，为什么还要学乘法分配律？”

学生对比后认为，应用乘法分配律可使计算更加简单。如25×3+25×17，先算加法，可使3和17凑整。25×（20+2）先算乘法，25×20=500，25×2=50，可2次分别凑整。

教师进一步追问：“运用乘法分配律一定能使计算简便吗？”

学生对比后认为，不一定。如25×4+25×10、25×（3+7）按一般法则计算更简便。

3.归纳提炼，养成意识。

教师提问：“你觉得乘法分配律的使用，需要满足什么条件？”

学生达成共识：先观察数据结构，判断是否符合乘法意义，看能否运用分配律；再根据数据特点，看是否能使计算简便；最后决定采用怎样的运算策略，逐步养成简便运算的意识（如图3）。

【教学活动4】建构与解构，熟练简便运算技能。

学生通过对运算对象的自主变换，进一步深入理解乘法分配律的内涵，厘清外延；把握概念的结构关联，在整体认知中逐步养成简便运算的意识，并形成相关技能。

教师可设计如下建构与解构的系列活动。

（1）建构1：创造1道应用乘法分配律后能简便计算的题目。

（2）建构2：创造1道应用乘法分配律后“看似能简便计算，实际不能”的题目。

（3）解构1：将不能简便计算的题目，改为能简便的。

（4）解构2：将能简便计算的题目，改为不能简便的。

【教学活动5】结构关联，把握内容的整体性，理解数学原理一致性。

学生回顾已学知识，进行纵向关联，整体把握学习内容（如图4）。

通过对比，学生明白了乘法分配律的内涵。事实上，前面学习中已经大量应用了乘法分配律，只是没有给出名称而已，其原理是一致的。

運算能力的提升是一个长期累积的过程，不是一蹴而就的。特别是合理、灵活的运算意识，需要学生不断的体验与感悟，由内部生发而成，不能依赖外部强制输入。利用原理一致性，结构化的递进体验，是一种比较有效的解决策略。这种原理一致性由此及彼，可推及其他运算内容的教学。