怎么引导学生探索长方形的面积公式

王畅畅

怎么做能更好地引导学生探索长方形的面积公式？教师可以设计以下教学活动。

一、“单位”识图，强化本质

1.试一试。让学生独立表示出图1中长方形的面积。

教师组织全班交流，让学生说思路：1个正方形是1[cm2]，2个正方形是2[cm2]，3个正方形是3[cm2]；列式就是：3×1[cm2]=3[cm2]。

2.算一算。让学生计算图2中长方形的面积。

学生独立完成后，全班交流，列出算式：（3[×]2）[×]1[cm2]=6[cm2]。

3.列一列。让学生列式计算图3中两个图形的面积，并说一说想法。

列出算式：（3[×]4）[×]1[cm2]=12[cm2]、（3[×]3）[×]1[cm2]=9[cm2]。

二、 “单位”助力，化虚为实

1.动一动。让学生计算图4中长方形的面积，引导学生量一量、摆一摆、画一画、列一列。

学生獨立完成后，教师组织全班交流，得出以下两种做法：

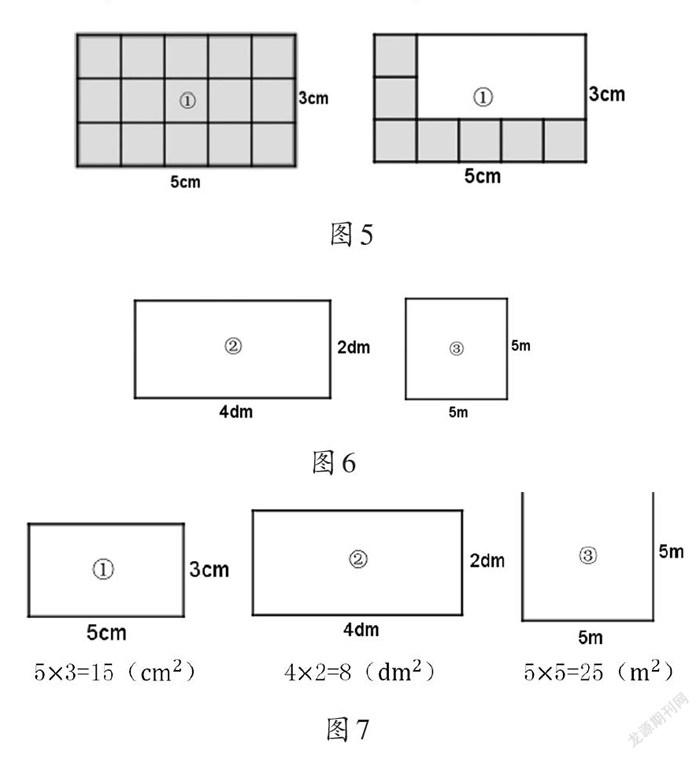
方法一：长方形中正好可以摆15个1[cm2]的正方形，面积是15cm2（如图5左）。

方法二：如果在长5[cm]，宽3[cm]的长方形内，摆正方形，每行能摆5个1[cm2]的正方形，可以摆3行，共15个，所以面积是15个1[cm2]，即15cm2（如图5右）。

教师引导比较：“两种方法有什么不同？你更喜欢哪一种？”学生得出方法二更简便，列式（5[×]3）[×]1[cm2]=15[cm2]。教师追问：“算式中5和3表示什么意思”。

2.理一理。让学生独立计算图6中图形的面积。

算式：（4[×]2）[×]1[dm2]=8[dm2]、（5[×]5）[×]1[m2]=25[m2]。让学生说一说，算式中各数分别表示什么意思？为什么两个算式中一个乘1[dm2]，另一个乘1[m2]？教师提问：“长方形的面积怎么计算呢？”引导学生归纳：（长[×]宽）[×]单位面积=长方形的面积。

3.比一比。教师出示图7，让学生对三个图形和算式进行比较，并组织讨论：“这样列式正确吗？为什么？”

师生归纳：长方形的面积=长[×]宽。

通过上述层层递进的探索活动，可以帮助学生理解长方形的面积本质上是对其所包含的面积单位的计数。