支座摩阻力对高速铁路大跨度悬索桥梁轨相互作用的影响

于向东，陈 卓，敬海泉,2

（1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075）

随着我国高速铁路的不断建设和发展，无缝线路的铺设也越来越普及，不仅是中小跨度桥梁，大跨度桥梁上也开始了无缝线路的铺设，进一步促进了桥梁-轨道系统相互作用的研究和发展。高速铁路大跨度桥梁空间跨度大，在温度、列车等荷载的作用下，梁体发生伸缩、挠曲，梁端转角增大，使无缝线路承受很大的附加力［1］。开展大跨度桥梁的梁轨相互作用研究，是保证高速铁路大跨度桥梁的安全运营和桥上列车行车安全的重要内容之一。

目前梁轨相互作用的相关问题已受到广泛关注，各国铁路部门也发布了相关的设计规范［2-4］。P.Ruge等［5-6］提出了有砟轨道在梁轨相互作用分析中考虑加载历史的非线性分析方法；戴公连等［7-8］建立了大跨度连续梁桥、梁拱组合桥以及斜拉桥的梁轨相互作用有限元计算模型，并进行了相关的验证分析；马战国［9］针对固定墩组和拉压连接器2种桥梁结构形式，依据桥梁轨道的相互作用关系建立了纵向力计算模型，分析计算长联连续梁桥无缝线路纵向力；颜轶航等［10］运用有限元软件AN⁃SYS 建立了某大跨度铁路斜拉桥梁轨相互作用有限元模型，通过计算分析得到列车制动过程中，钢轨制动附加力峰值产生于斜拉桥梁端的结果。

在一般桥梁的设计和研究过程中，滑移支座摩阻力相对较小，为了简化计算，常常忽略桥墩上滑移支座摩阻力的影响，并假定滑移支座处梁端可自由伸缩，固定支座所在桥墩承受所有水平力［1，11-14］。对于中小跨度铁路桥梁，在计算桥梁-轨道系统的纵向附加力过程中，支座摩阻力的影响可以忽略不计［14］。但大跨度铁路桥梁的恒载大、跨度长，当桥梁发生纵向移动时，其滑动支座摩阻力远大于中小跨度桥梁，支座摩阻力对大跨度铁路桥梁梁轨相互作用的影响也将远远大于中小跨度桥梁［15］，且根据UIC 774-3规范，不考虑活动支座摩阻力，对于桥梁活动支座所在墩是不利的，可能导致桥墩的实际安全系数偏低，影响结构的安全稳定。因此，高速铁路大跨度悬索桥上滑动支座摩阻力的存在将会对桥梁-轨道系统的纵向附加力产生一定的影响。此外，悬索桥以柔性缆索为主要受力构件，其刚度主要是由主缆提供，会随着桥梁变形同时更新，具有显著的几何非线性［16］，且目前活动支座摩阻效应对悬索桥的研究较少，影响规律尚不明确。在此，本文进行支座摩阻力对高速铁路大跨度悬索桥梁轨相互作用影响的研究。

1 梁轨相互作用

桥梁在温度、列车等荷载作用下，梁体会产生纵向伸缩位移，进而通过梁轨间的各种纵向约束带动钢轨产生纵向伸缩位移，并在钢轨中产生纵向附加力。而该纵向附加力又会反过来影响梁体，并向支座传递，根据各支座摩阻力以及各桥墩的刚度分配纵向附加力，影响墩台的纵向变形，因此，梁体和墩台的纵向变形与钢轨的纵向附加力是一个相互制衡、相互协调的耦合系统，这种相互影响的作用被称为梁轨相互作用。梁轨相互作用的基本微分方程为

式中：uΔ为梁体位移；u为梁轨相对位移；r(u)为梁轨间纵向阻力；E为钢轨的弹性模量；A为钢轨截面的面积。

梁体位移uΔ包含了因伸缩或挠曲产生的纵向位移u0和墩台在以上因素作用下受到水平力而产生的墩顶纵向位移uδ。与钢轨相比，桥梁的主梁刚度大很多，所以u0受钢轨约束的影响很小，主要与桥梁的自身约束、温度变化及列车的运行有关。uδ则与墩的高度，结构以及其基础有关。

为了简化计算，在以往研究中常常忽略支座摩阻力的影响，并假定滑动支座处梁端可以自由伸缩，固定支座所在墩承受所有水平力。则梁体任一点的位移uΔ(x)可以表示为

然而在实际工程中，摩阻力为0 的活动支座是不存在的，由于支座摩阻力F的存在，活动支座所在墩会对水平力起到一定的分担作用，改变了纵向附加力在墩台之间的分布。考虑滑动支座摩阻力后，滑动支座处梁端的变形会相应减小，变为

此时，梁轨相对位移u也会发生相应的改变。由于梁体、墩台和钢轨的耦合作用，钢轨附加力必然也会发生改变。计入支座摩阻力后，活动墩将与固定墩共同分担纵向附加力，纵向附加力在桥墩、台间的分配规律也将发生改变。

2 工程背景

本文以某高速铁路大跨径悬索桥为工程背景，该桥立面图如图1所示。

图1 某高速铁路大跨径悬索桥立面图（单位：m）

该桥是双塔半漂浮体系地锚式悬索桥，跨度布置为（84+84+1 092+84+84）m，主跨为1 092 m，全长1 432 m，主桥为双塔5 跨连续钢桁梁悬索桥，钢桁梁为板桁结合加劲梁，横断面采用带副桁的直主桁形式，桁架形式为华伦式桁架。全桥采用2根平行主缆，横向中心间距为43 m，主跨矢跨比1/10。大桥设计为双层桥面，双层桥面系均采用正交异性板结构，上层为双向8车道高速公路，设计行车速度为100 km· h-1；下层为4线铁路，其中2线为客运专线，设计时速为250 km，预留2线铁路设计时速为200 km，4 线铁路采用有砟轨道，CHN60 型钢轨、带有挡肩的Ⅲc混凝土轨枕和与轨枕配套的弹条Ⅴ型扣件。南北两侧桥塔为钢筋混凝土框架结构，桥塔横桥向为门式框架结构。悬索桥南北两侧对称设置边墩和辅助墩，为箱形截面钢筋混凝土门式墩。边墩、辅助墩及桥塔下弦各支承点均采用球形支座，纵向均能自由活动，且在主塔下弦处设置了黏滞阻尼器，以承受制动作用下的瞬时冲击荷载，悬索桥上支座及阻尼布置如图2所示。

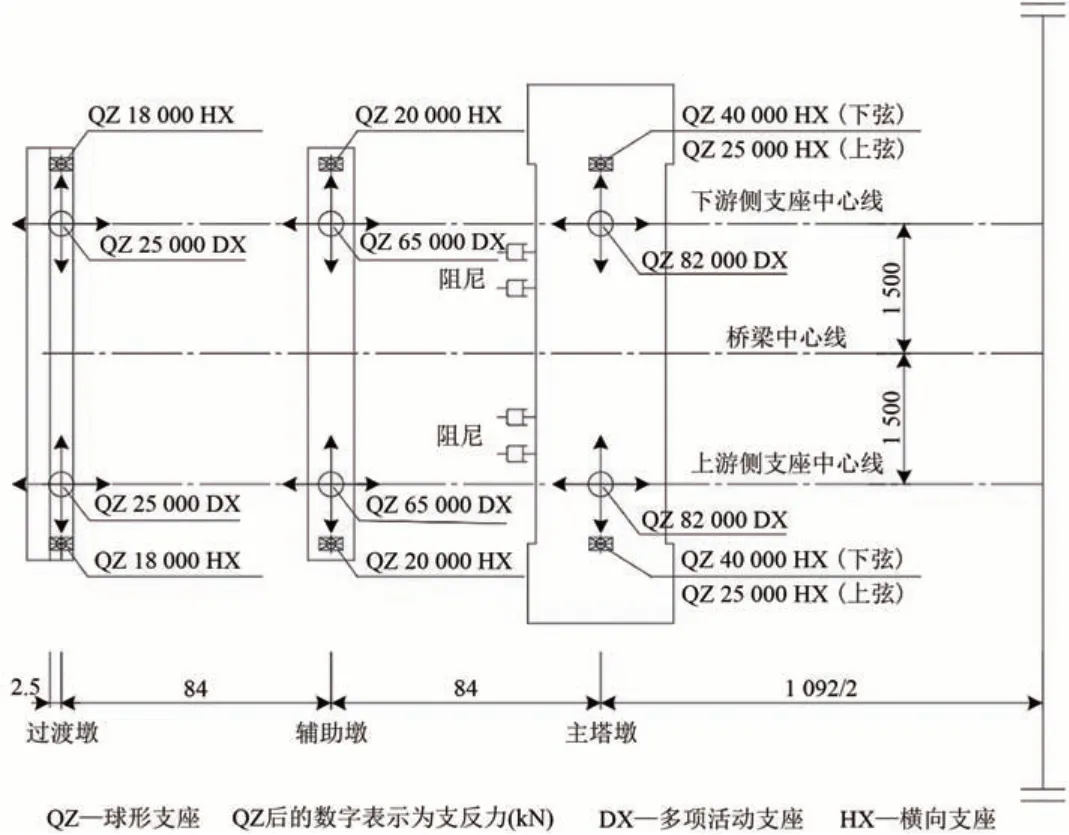
图2 悬索桥上支座及阻尼布置（单位：m）

3 悬索桥桥梁-轨道-塔墩空间一体化有限元分析模型

为了方便计算，本文在模型建立过程中采用以下假设。

（1）假设固定墩固定支座处梁完全无法伸缩；

（2）不考虑支座本身的纵向变形，忽略支座本身的纵向刚度；

（3）不考虑梁端道砟断面传力效应，假定道床传递的纵向力均由墩台承受。

在上述假设条件下，本文基于通用有限元软件ANSYS，建立悬索桥桥梁-轨道-塔墩空间一体化有限元分析模型，如图3所示。

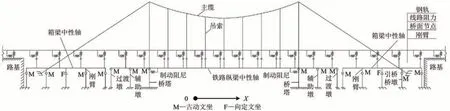
图3 悬索桥梁轨相互作用空间一体化分析有限元模型

本桥加劲梁的上弦杆、下弦杆、竖杆、斜杆、斜撑、桥面系纵横梁以及纵向加劲肋等主要受力构件，主塔、过渡墩、辅助墩以及钢轨采用空间梁单元模拟，横联与竖杆、上支点横梁之间采用刚臂单元模拟；主缆、吊索采用空间杆单元模拟。根据桥上实际钢轨数目建立钢轨单元，每条钢轨的节点间距选取为钢桁梁铁路桥面系中相邻横梁的间距，钢轨材料选用简化了的理想弹性本构关系进行模拟，不考虑进入塑形状态。采用弹簧单元连接钢轨节点和与钢轨节点对应的铁路桥面节点，用以模拟梁轨间竖向、横向和纵向线路阻力，其中竖向、横向阻力采用线性弹簧单元模拟，纵向阻力采用非线性弹簧单元模拟。采用空间梁单元，利用其轴向受力，模拟制动阻尼器的制动作用。为了更加直观地揭示悬索桥上无缝线路受力和变形的相关规律，突出主桥梁端梁轨相互作用变化特性，本文在不设置伸缩调节器的基础上进行相关研究。

对于边界条件，主缆的锚固点和桥塔底部以及桥墩墩底均固结；按照主缆与桥塔顶部的实际约束状态施加约束，对主缆与主塔顶部节点的Y和Z方向的平动自由度进行耦合，其余方向均自由，并取路基长度182 m。桥塔主要为受压构件，为保证不承受弯矩，不约束主塔顶点顺桥向平动自由度。

桥梁支座竖向、横向、转动均采用相应参数刚度的线性弹簧单元模拟。由于引桥固定支座纵向不能移动，则采用大刚度的线性弹簧单元模拟。为了考虑活动支座摩阻力的影响，采用了组合弹簧单元模拟滑动支座摩阻力。参照文献［17-18］，采用双线性理想弹塑性滞回阻力模型模拟滑动支座的摩阻特性，如图4所示。图中：uD为墩顶与梁节点的相对位移；F为支座的纵向摩阻力；临界摩阻力为Fx；uDx为支座的临界滑动位移，参照文献［15，17］，本文取uDx=0.002 m；Kb为支座开始滑动后的恢复力刚度，参照文献［18］，本文取Kb=0。

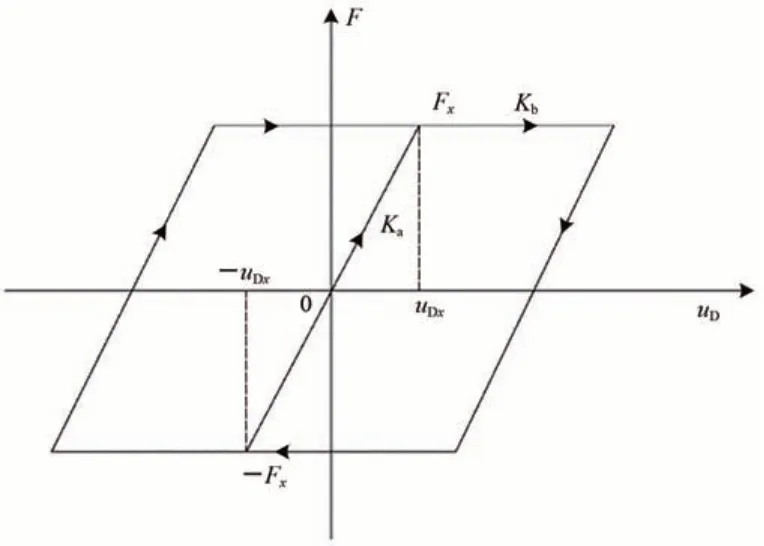
图4 滑动支座双线性恢复力模型

滑动的临界摩阻力为

式中：μ为滑动摩阻系数；Fy为单个支座的竖向承载力。

由此可知初始刚度

各支座所处塔墩位置如图1 和图2 所示，其中N2 和S2 为固定墩，其余均为活动墩。各活动支座参数见表1。

表1 活动支座竖向参数

4 支座摩阻力对梁轨相互作用的影响

梁轨间道床纵向阻力按《无缝铁路设计规范》选取，如图5所示。钢轨所受的各纵向附加力及产生的位移从4线铁路中的最外侧钢轨中提取，钢轨纵向水平坐标零点位于北塔3#中心线上，定义梁体和钢轨位移向南侧（见图1）伸长为正，钢轨应力受拉为正，梁轨相对位移为钢轨与纵梁位移之差。

图5 梁轨间纵向阻力模型

为了研究支座摩阻力对大跨度高速铁路悬索桥梁轨相互作用的影响，滑动支座摩阻系数参照UIC 774-3和文献［15，19］进行选取，分别取为0（不计摩阻力）、0.03（常温工作）、0.05（低温工作）和0.10（长期使用）共4个值来计算纵向附加力、梁轨相对位移及墩顶水平力。

4.1 伸缩附加力

悬索桥在温度作用下产生纵向伸缩变形，从而引起钢轨内部产生纵向附加力。计算悬索桥上伸缩附加力时，参照《无缝铁路设计规范》，按照钢桁梁升温25 ℃，引桥混凝土梁升温15 ℃进行计算。温度作用下计算结果如图6所示，温度作用下钢轨伸缩力及钢轨纵向位移最值见表2。

从图6和表2可知：随着滑动支座摩阻系数的增加，悬索桥上钢轨伸缩附加力变化很小，跨中部分钢轨拉应力基本不变，梁端的钢轨压应力略微增大；考虑滑动支座摩阻力后，钢轨纵向位移明显降低，且随着摩阻系数的增大而减小，摩阻系数为0.03，0.05和0.1时的钢轨纵向位移最大值分别为不考虑滑动支座摩阻力的87.75%，79.76%和59.78%；在考虑滑动支座摩阻力后，活动墩（滑动支座所在墩）将分担固定墩所承受的纵向力，随着摩阻系数的增大，固定墩N2和S2的墩顶伸缩水平力逐渐减小；而活动墩则相反，其墩顶伸缩水平力随着摩阻系数的增大而增大，且与边墩相比，2#和5#辅助墩以及3#和4#主塔处墩顶伸缩水平力的增幅更加明显。

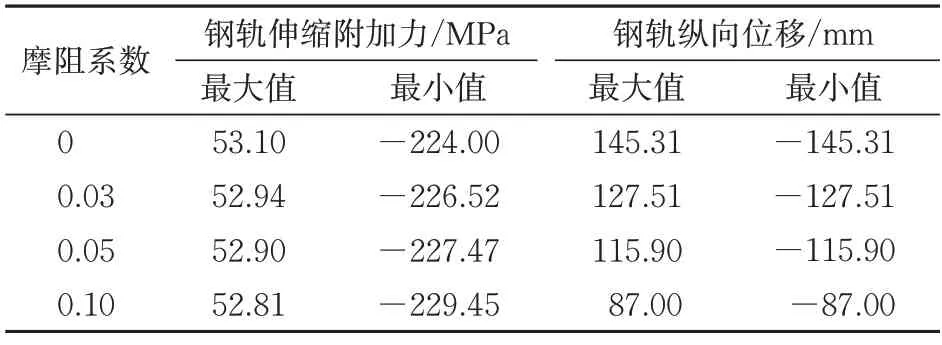
表2 温度作用下钢轨伸缩力及钢轨纵向位移最值

图6 温度作用下计算结果

4.2 挠曲附加力

桥梁在列车竖向作用下产生挠曲变形，从而对钢轨产生纵向附加力。根据《铁路列车荷载图式》［20］选取ZK 列车活载加载，加载长度取550 m（根据《高速铁路设计规范》［21］，加载长度可按照车站的到发线长度取值，规定的车站到发线有效长度650 m减去两侧50 m的安全距离，得到允许容纳的列车最大编组长度为550 m）。由于本桥跨度较大，列车加载位置对钢轨纵向附加力也会产生一定的影响。在此，本桥列车荷载设置了2 种工况，工况1为偏载，列车从北主塔向跨中加载；工况2 对称加载，列车从跨中向南北两侧加载。对比偏载工况1和对称加载工况2，分析滑动支座摩阻系数对桥梁-轨道系统挠曲附加力的影响。偏载工况下的计算结果如图7所示，钢轨挠曲附加力和梁轨相对位移最值见表3；对称加载工况下的计算结果如图8所示，钢轨挠曲附加力和梁轨相对位移最值见表4。

图7 偏载工况下计算结果

表3 偏载工况下钢轨挠曲附加力和梁轨相对位移最值

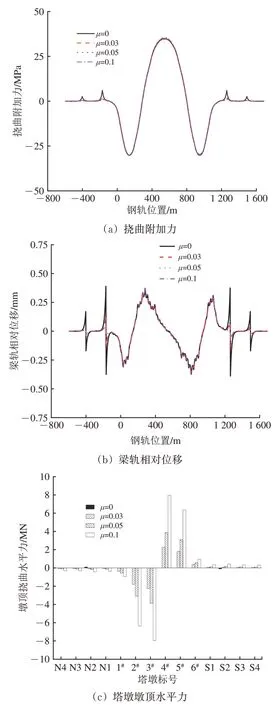
图8 对称加载工况下计算结果

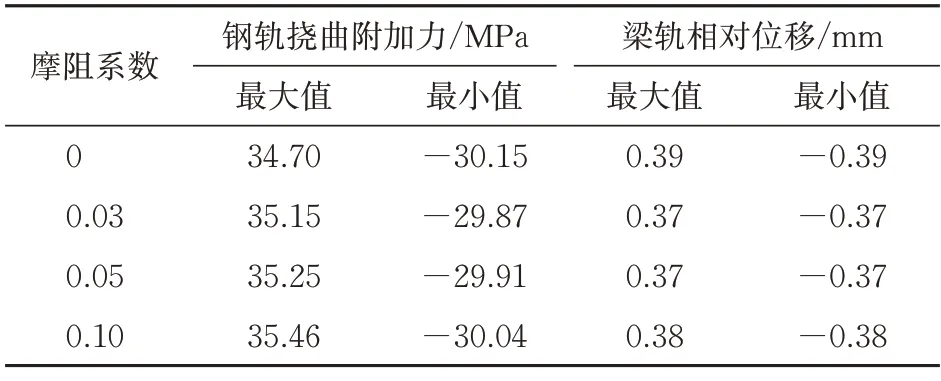
表4 对称加载工况下钢轨挠曲附加力和梁轨相对位移最值

根据图7 和表3 可知，在偏载工况下，不考虑滑动支座摩阻力（μ=0）时，钢轨挠曲附加力的拉应力最大值是μ为0.03，0.05和0.1时的2倍以上，支座摩阻系数分别为0.03，0.05和0.1时，钢轨挠曲附加力的压应力最大值分别是不计摩阻力时的58.65%，54.67%和53.39%；考虑滑动支座摩阻力后，随着μ的增大，钢轨挠曲力虽然继续减小，但减小幅度较低，钢轨挠曲力的最大拉应力从μ=0.03 时的62.14 MPa 减小到μ=0.1 时的56.57 MPa，减小幅度仅为9%，而钢轨挠曲力的最大压应力几乎不变；与不考虑滑动支座摩阻力相比，μ=0.03时梁轨相对位移由16.97 mm减小到5.47 mm，减小了68%，随着μ的增大，梁轨相对位移继续减小，但减小幅度较小；计入滑动支座摩阻力后，随着滑动支座摩阻系数的增大，北侧所有墩墩顶水平力逐渐增大，其中2#和3#的幅度最大，3#最大墩顶挠曲水平力达-8 200 kN；南侧墩除5#号墩外，其余墩墩顶水平力均是先减少，后增加，在此过程中力的方向发生了改变，所有墩中4#和5#变化幅度最大，5#最大墩顶挠曲水平力达6 277 kN。μ从0.05到0.1的过程中，4#墩顶水平力方向甚至发生了改变；在偏载作用下，靠近荷载的北侧墩塔的墩顶水平力比南侧更大。

由图8 和表4 可知：在对称加载工况下，随着滑动支座摩阻系数的增大，钢轨挠曲附加力的最大值和最小值变化并不明显，但悬索桥梁端钢轨拉应力却发生了明显的变化，与不考虑滑动支座摩阻力相比，μ=0.03 时梁端钢轨拉应力减小了64%，考虑支座摩阻力后，梁端钢轨拉应力随着摩阻系数的增大而逐渐减小；滑动支座摩阻系数的改变对梁轨相对位移最大值、最小值影响很小，但梁轨相对位移最大值、最小值的位置发生了变化；不考虑滑动支座摩阻系数时，梁轨相对位移最大值、最小值出现在南北两侧梁端；考虑滑动支座摩阻系数后，最大值、最小值位置变为对称加载的荷载两端；考虑滑动支座摩阻力后，全部墩的墩顶挠曲水平力均随着摩阻系数的增大而增大；与边墩相比，2#和5#辅助墩以及3#和4#主塔承担了大部分纵向水平力，其墩顶挠曲水平力的增幅也更加明显。

对比偏载和对称加载工况可以发现：当列车荷载为偏载时，与不计滑动支座摩阻力相比，考虑支座摩阻力后，钢轨挠曲附加力和梁轨相对位移均显著减小；而当列车荷载对称时，此时梁轨相对位移较小，支座摩阻力对其大小影响有限，但梁轨相对位移最大值、最小值的位置发生了改变，钢轨挠曲附加力最大值、最小值几乎不变，梁端钢轨应力发生轻微变化；在列车荷载下，滑动支座摩阻力对墩塔顶水平力的分布具有很大的影响，计入滑动支座摩阻力后，墩塔顶水平力会重新分布，部分之前不承受纵向水平力的活动支座墩顶将会承受巨大的纵向水平力。

4.3 制动附加力

列车在桥上启动或制动时在钢轨内部产生纵向附加力。按照《无缝铁路设计规范》，轮轨黏着系数取0.164，参照文献［1］，取列车制动长度400 m（按16 节编组计算），制动力计算列车加载工况同4.2。2种列车荷载工况下制动的计算结果如图9—11所示，钢轨制动附加力和梁轨相对位移最值见表5。

图9 2种列车荷载工况下制动时最大钢轨制动附加力

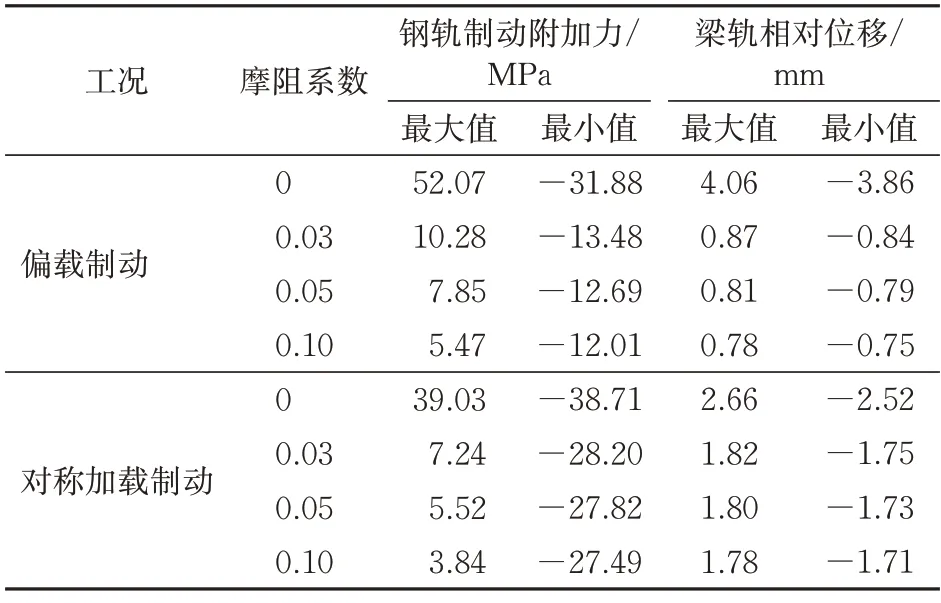
表5 偏载和对称加载工况下制动时的制动附加力和梁轨相对位移最值

由图9、图10 和表5 可知：与不计滑动支座摩阻力（μ=0）相比，计入摩阻力后，偏载和对称加载工况下制动时钢轨制动附加应力拉应力和压应力最大值均迅速减小，但随着摩阻系数的增大，钢轨制动附加应力的最值变化并不显著；偏载制动时制动附加应力拉应力最大值均大于对称加载制动时，而偏载制动时压应力最大值均小于对称加载制动时；计入支座摩阻力后，2 种制动工况下两侧梁端处的梁轨相对位移均随着摩阻系数的增大而减小，但偏载条件下的变化要比对称加载更加显著，而跨中部分的梁轨相对位移均接近于0。

图10 2种列车荷载工况下制动时梁轨相对位移

由图11可知：在考虑滑动支座摩阻力后，2种荷载工况制动时活动墩墩顶制动水平力均随着摩阻系数的增大而增大；从不计滑动支座摩阻力（μ=0）到计入摩阻力（μ=0.03），固定墩N2 和S2 的墩顶水平力先减小，之后随着摩阻系数的增大而增大；2种工况下，在计入支座摩阻力后，均由2#和5#辅助墩以及3#和4#主塔承担了大部分纵向水平力。

图11 2种列车荷载工况下制动时塔墩墩顶水平力

4.4 断轨附加力

在低温条件下，钢轨可能会因强度不足而发生断裂，通常在附加应力较大处会且只会有一根钢轨发生断裂并形成裂缝，温度变化产生的附加力则储存在另一根钢轨上，而2 根及以上钢轨断裂的概率极低，故不考虑［11，22-23］。《无缝铁路设计规范》规定断缝容许宽度不得超过70 mm。由于温度变化时钢轨附加应力在梁端处最大，假设北侧梁端位置处钢轨发生断裂，分析不同滑动支座摩阻系数下钢轨断裂时的钢轨位移及墩顶断轨水平力，结果如图12和图13 所示。计算断轨力时，按该悬索桥最大降温52 ℃，主桥钢桁梁降温25 ℃，引桥混凝土梁降温15 ℃［12，22］取值。

图12 不同滑动支座摩阻系数时断轨后钢轨位移

图13 不同滑动支座摩阻系数时断轨后塔墩墩顶水平力

由图12 可知：钢轨在北侧梁端位置处断裂时，若不考虑支座摩阻效应（μ=0），钢轨断缝值为217.91 mm，当滑动支座摩阻系数分别为0.03，0.05和0.1时，钢轨断缝值分别减小为206.28，197.81和171.93 mm，均超过了规范要求的70 mm限值，需设置钢轨伸缩调节器。由图13 可知：随着支座摩阻系数的增大，固定墩N2和S2所承受的墩顶水平力逐渐减小，而活动墩承受的墩顶水平力逐渐增加，其中跨中3#和4#主塔及2#和5#辅助墩的增幅与其他活动墩相比更加显著。

5 结论

（1）对于高速铁路大跨度悬索桥，不考虑滑动支座摩阻力时，列车荷载偏载及列车制动荷载作用下钢轨的各项附加应力计算值均明显偏大，而温度荷载和列车荷载对称加载时的影响却很小。支座摩阻系数分别为0.03，0.05和0.1时，列车荷载偏载工况下钢轨最大挠曲附加应力分别是不计摩阻力时的58.65%，54.67%和53.39%，钢轨最大制动附加应力分别是不计摩阻力时的42.28%，39.80%和37.67%，列车荷载对称加载工况下钢轨最大制动附加应力分别是不计摩阻力时的72.85%，71.87%和71.01%。不同摩阻系数下，钢轨的制动附加力、偏载下的挠曲附加力差距较小，但钢轨的各项附加应力仍呈现出随着摩阻系数的增大而逐渐减小的趋势。

（2）不考虑滑动支座摩阻力时，只有固定墩承受墩顶水平作用力，活动墩不承受纵向力；计入支座摩阻力后，活动墩将与固定墩共同承担纵向水平力，各活动墩的墩顶纵向水平力均随着摩阻系数的增大而增大，其中3#和4#主塔及2#和5#辅助墩的增幅尤为显著，其承担了绝大部分的纵向水平力。

（3）列车荷载位置对不同滑动支座摩阻力下的挠曲附加力影响很大，对制动附加力却影响较小。偏载工况下，挠曲附加力在滑动支座摩阻力的影响下会显著减小，其最大压应力从不计摩阻力的105.95 MPa，分别减少到支座摩阻系数为0.03、0.05和0.1时的62.14，57.92 和56.57 MPa；而对称加载工况下，支座摩阻力对挠曲附加力影响却很小。偏载和对称加载工况下制动附加力均会受到支座摩阻力的影响而减小，偏载时制动附加力的最大压应力从不计摩阻力的31.88 MPa，分别减少到支座摩阻系数为0.03、0.05和0.1时的13.48，12.69和12.01 MPa；对称加载时制动附加力的最大压应力从不计摩阻力的38.71 MPa，分别减少到支座摩阻系数为0.03、0.05 和0.1 时 的28.20，27.82 和27.49 MPa。

（4）在断轨作用下，随着滑动支座摩阻系数的增大，断轨后钢轨断缝宽度逐渐减小，当支座摩阻系数为0.03、0.05和0.1时，钢轨断缝宽度由217.91 mm分别减小为206.28，197.81和171.93 mm。

可见，滑动支座摩阻力对高速铁路大跨度悬索桥上梁轨相互作用具有明显的影响。整体而言，滑动支座摩阻力对列车荷载偏载下的挠曲附加力、制动附加力和断轨附加力影响更大，对伸缩附加力和列车荷载对称加载下的挠曲附加力影响较小。