基于轴箱垂向振动加速度的波磨谷深值估算方法及应用

牛留斌，祖宏林，徐晓迪，王韫璐

（1.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081；2.中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081）

波磨现象是困扰轨道交通的技术难题，波磨恶化轮轨关系，辐射噪声污染环境，还降低线路质量，增大车辆动力损耗，加速车辆轨道部件疲劳伤损，增加工务部门维护工作量和维修成本。如不及时整治，波磨不仅影响旅客乘坐舒适度，严重时还会诱发轨道结构局部破坏进而危及行车安全。国际上迄今为止尚未形成普适性的波磨成因理论和整治策略，但作为铁路行业重点研究课题，特定类型波磨的萌生和发展已得到合理解释，比如：Grassie等［1-3］在总结既有文献及其个人研究成果的基础上，按照波长固定机理及损伤机理将波磨分为Pinned-Pinned 共振型、车辙槽型、重载型、轻轨型、P2 力共振型、其他特殊轨道结构型6 大类型，并探讨了各种类型波磨形成机理、预防对策及整治措施；Nielsen 等［4-6］综述不同线路上25～80 mm短波长波磨病害分布规律及特征参数，在对波磨成因进行合理假设的基础上，从理论和试验的角度解释了波磨发展规律。在理论研究指导下，为改善轮轨关系、降低接触应力，减缓波磨生长速率的抑制方法如提高钢轨表面材料硬度［7］、增加摩擦调节器［8］、轨道吸振器及定期打磨作业等措施已用在工程实践中。钢轨打磨作业能够显著延缓波磨过快发展，已成为铁路行业广泛采用的维修手段［5，8］，打磨决策以轨面粗糙度水平［9］或谷深值［10］作为制定依据。

相对于“天窗”时段内人工上道测试轨道不平顺或粗糙度查找波磨的作业模式，车载设备能够高效、客观地评价轨面状态而广泛地应用于线路监测中。常见车载技术如基于惯性基准法［11-12］通过测试车体振动加速度反演轨道不平顺，滤波得到不同波长区段的轨面粗糙度，以轨面粗糙度水平［9］评价轨面状态及是否需要打磨作业；激光摄像技术［13］通过高精度摄像机采集轨面廓形图像，采用激光峰值检测信号提取技术重构三维空间曲线并转换轨道不平顺，利用正弦函数拟合轨道不平顺获得波磨特征参数；超声波和涡流检测［14］则通过分析异常超声脉冲或涡流时频域响应信号的频谱分布，实现不同深度波磨缺陷的检测与识别；轴箱振动加速度传感器［15-17］和测力轮对［18-19］等设备能够实时测试轨道激励的车辆动力学响应，借助信号特征提取和数据处理技术挖掘波磨区段表征指标进而评价轨面状态。轴箱振动加速度传感器易于安装、便于维护、经济适用性强，因而被广泛地应用于轨道短波状态监测［20］中。轴箱垂向振动加速度幅值因具有离散性不能直接用于评价波磨状态，工程上常用其衍生指标量化波磨严重程度，如Tanaka 等［16］拟合了波磨区段检测车导向轴位上轴箱垂向振动加速度有效值与轨面平均粗糙度之间的函数关系，再依据波磨整治时轨面粗糙度门槛值得到轴箱垂向振动加速度有效值的阈值，以此阈值为基础提出了实测轴箱振动加速度有效值归一化算法；为抑制车辆运行速度对波磨评价的影响，Bocciolone 等［15］以轴箱振动加速度的滑动有效值除以车辆运行速度为修正指标，通过曲线段轴箱振动加速度实测数据拟合下股钢轨波磨谷深值与修正指标之间的表达式；Caprioli等［21］利用轴箱垂向振动加速度，将连续小波变换系数表征为频域的能量，采用实测数据建立频域能量与曲线波磨区段轨道不平顺之间对应关系，实现波磨状态的评价；为消除检测车辆性能差异对评价结果的影响，刘金朝等［22-23］将时域轴箱垂向振动加速度经希尔伯特-黄变换［24］至频域，引入能量因子识别波磨周期性的显著程度，以归一化钢轨波磨指数量化波磨状态的严重程度。以上既有文献主要研究了波长相对固定时轴箱垂向振动加速度衍生指标与波磨谷深值之间在时频域上的映射关系，考虑波长因素对映射关系的影响较少。波磨波长是影响轮轨相互作用的敏感因素［25-26］，直接影响着轴箱垂向振动加速度的频率和幅度，因此开展波长与轴箱垂向振动加速度之间关联性研究有助于深入认识波磨激励车辆振动的响应特性，从而摸索出基于轴箱垂向振动加速度评价钢轨波磨状态的科学方法。

本文基于CRTS Ⅱ型板式轨道及CRH3型动车组拖车参数构建轮轨动力学模型，仿真研究300 km·h-1速度时波磨激励下轴箱垂向振动加速度时频域特征，以拉依达准则选取轴箱垂向振动加速度3σ大值为波磨状态表征指标，采用非线性最小二乘法和非理式方程拟合波长40～180 mm 表征指标与波长谷深之间的函数关系，分析拟合参数的物理意义及影响因素。在此基础上推导波磨谷深值评估算法，高铁波磨现场应用效果说明了该方法可为我国高铁线路波磨状态的评价和打磨整治决策提供科学支撑。

1 轮轨动力学模型构建

1.1 模型构建

车辆通过钢轨波磨区段时轮轨垂向相互作用的频率为

式中：f为波磨激励频率，Hz；v为车辆运行速度，mm· s-1；λ为波长，mm。

由式（1）可知，波长λ在40～180 mm、车辆运行速度v大于250 km·h-1时波磨激励频率大于385.8 Hz，该频段轴箱垂向振动响应特性与车辆一系悬挂装置、构架、车体等部件运动关系较小［27］，因此，在研究直线工况下钢轨波磨区段轮轨垂向振动特性时可将车辆一系悬挂以上部件简化为质量块m，而车辆一系悬挂简化为横向刚度K0、阻尼C0和垂向刚度K1、阻尼C1的弹簧单元施加在轮对两侧端部，弹条、轨下垫板、缓冲垫板等扣件系统对钢轨垂向支承作用由刚度K2、阻尼C2的弹簧单元模拟。轮轨动力学模型结构简图如图1所示。

图1 轮轨动力学模型结构简图

前轮起始位置o点为坐标原点，钢轨中部ab段为波磨区段，c点为仿真结束位置。车辆沿z轴方向运行，沿y轴方向沉浮运动。轮对、钢轨、道床均采用真实尺寸建模，其中车轮为CRH380B 型动车组采用的LMB型踏面的拖车车轮，钢轨为CN60型钢轨、1∶40 轨底坡。轮轨动力学模型实体单元构成如图2 所示。图2 中轨道长度为26.65 m，轨枕间距为650 mm。轮轨材料弹塑性本构关系采用双线性硬化模型模拟，轴箱垂向振动加速度数据来自前轮仿真结果。

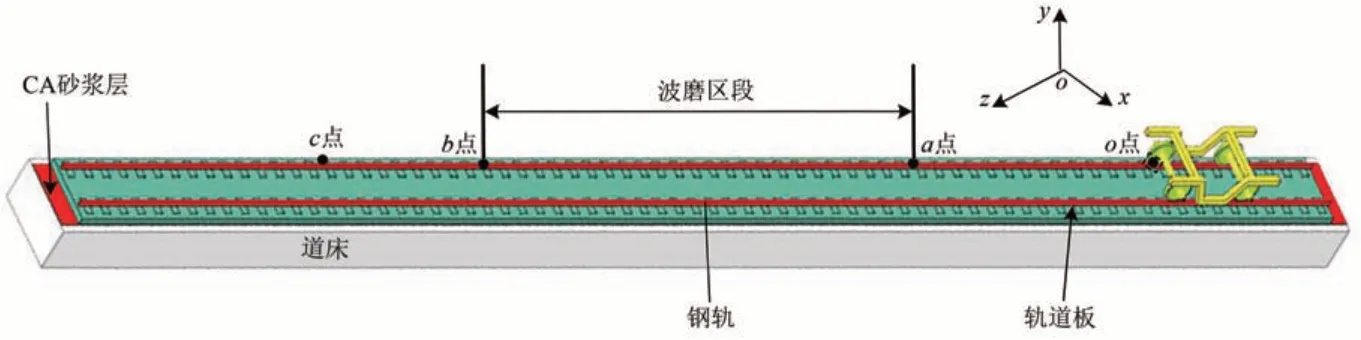
图2 轮轨动力学实体单元构成

在轮轨接触面法线方向采用“面-面”硬接触算法计算轮轨法向接触力，切线方向采用干燥条件下轮轨相互作用时的库伦摩擦系数0.3［28］，后轮与钢轨端部的距离不小于3 m，并在轨道端部施加面对称约束以减少有限长度钢轨端部反射波对计算结果的影响。

为缩减轮轨动力学模型规模和计算时间，实体单元网格尺寸与其受关注程度有关，靠近轮轨接触区域单元网格尺寸较小，在钢轨底部、非钢轨波磨区段、轮轴、车轮幅板、砂浆层、道床等远离关注区域的单元网格尺寸较大。轮轨接触面上单元设置为2 mm×2 mm×2 mm 正六面体网格，如图3（b）右上方放大图所示，每组扣件由55 根弹簧组成的面弹簧模拟如图3（b）右下方放大图所示。图中：M为牵引扭矩［29］。

图3 轮轨动力学网格模型

为减少轮轨动力学模型在oa段钢轨达到动态平衡所需时间，先采用隐式算法计算重力载荷下模型静平衡状态，将其作为显式计算的初始边界条件，轮对施加速度载荷运行至钢轨a点时模型处于动态平衡状态。为确保轮对匀速运行，在车轮上施加牵引扭矩M以减少轮轨摩擦力对运行速度的影响，即有

式中：Fz为轮轨力F沿z轴方向分量，kN；R为车轮滚动圆半径，430 mm；J为轮对转动惯量，kg·m²；ε为轮对角加速度，车辆匀速运行时ε=0。

在不考虑轮对横向运动前提下，Fz为

式中：Fn为轮轨力F沿轮轨接触面法向分量，kN；μ为牵引系数，取0.03［30］。

在ABAQUS 软件显式模块中采用中心差分法求解轮轨实时运动状态和接触力，每个时间增量步结束时刻状态完全由该增量步开始时刻的位移、速度、加速度计算得到［31］。最大积分时间步长Δt由轮轨动力学模型最高固有角频率ωmax决定，满足

式中：ζ为轮轨系统的临界阻尼比；Le为模型单元长度，mm；cd为模型材料特性决定的波速，m ·s-1；E为轮轨材料弹性模量，GPa；ρ为轮轨材料的密度，mg· mm-3。

由式（4）可知，最小网格尺寸为2 mm 时最大积分时间步长Δt为10-7s 数量级，说明图3 轮轨动力学模型能够计算极短时间内轮轨接触力、位移等物理量，模拟波磨激励下轮轨间高频动力学行为。

1.2 波磨施加

钢轨波磨区段轨道不平顺由多种随机波长成分叠加而成，其激励的轴箱振动加速度中也包含多种频率成分，但在特定高铁线路上运行车辆型式、车辆运营速度、轨道类型等相对稳定，易形成固定波长的钢轨波磨［1-3］。轻型及重型波磨区段钢轨顶部呈现等波长连续分布特征如图4 所示。图中：b1和b2分别为波磨区段轨面光带最小和最大宽度半值。

图4 不同程度的钢轨表面状态

波磨区段轨道不平顺采用余弦函数曲线模拟，通过修改钢轨模型单元网格节点坐标的方式施加波磨。波磨区段某节点n（x，y，z）的坐标修改量Δ(x，y，z)与其坐标有关，为

式中：d为谷深值，mm；za和zb分别为波磨区段起止位置在z轴上的坐标，mm。

由图4（b）可知，波磨区段某一轨道横剖面上的谷深值并不是沿x轴方向均一分布的，为此采用xoy平面内抛物线函数形式修正Δ(x，y，z)，修改量δ（x，y，z）为

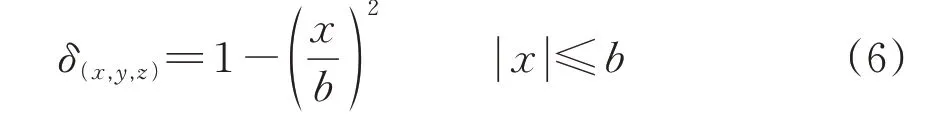
式中：b为波磨宽度的半值，mm。

由图4（b）还可知，波磨宽度沿z方向呈现周期性变化，其波长与波磨波长一致，构造余弦函数表征波磨沿x轴方向上宽度变化特性，为

根据现场测试结果，正常光带宽度约为25 mm，波磨宽度大于正常光带宽度，约在30～40 mm之间。因此，式（7）中b1和b2分别取15和20 mm。

为避免单元网格节点坐标过度修改引起单元畸形从而影响仿真精度，在施加波磨时仅修改ab段钢轨全部的节点坐标。施加波磨时节点n（x，y，z）修正为修正过程示意图如图5所示。修正后坐标为

图5 波磨施加时单元网格坐标修正过程示意图

其中，

式中：θ为钢轨1∶40 轨底坡的角度；h为CN60 型钢轨高度，176 mm；dn为节点n处波磨的谷深值。

施加轨道不平顺后轮轨动力学模型波磨区段钢轨表面形状如图6 所示。图中：蓝色表示正常轨面，由蓝色至红色表示谷深值依次增大。由图6 可知：波磨区段在yoz平面内沿z轴方向呈现多波余弦曲线形状分布；在xoz平面内波磨谷深值沿x轴呈现抛物线形状分布，越靠近钢轨顶部中心线波磨谷深值越大，而远离钢轨顶部中心线波磨谷深值逐渐减小，与图4中波磨现场轨面形状分布规律一致。

图6 轮轨动力学模型波磨区段轨面形状示意图

除了特别标注外，图3 所建轮轨动力学模型参数取值见表1。

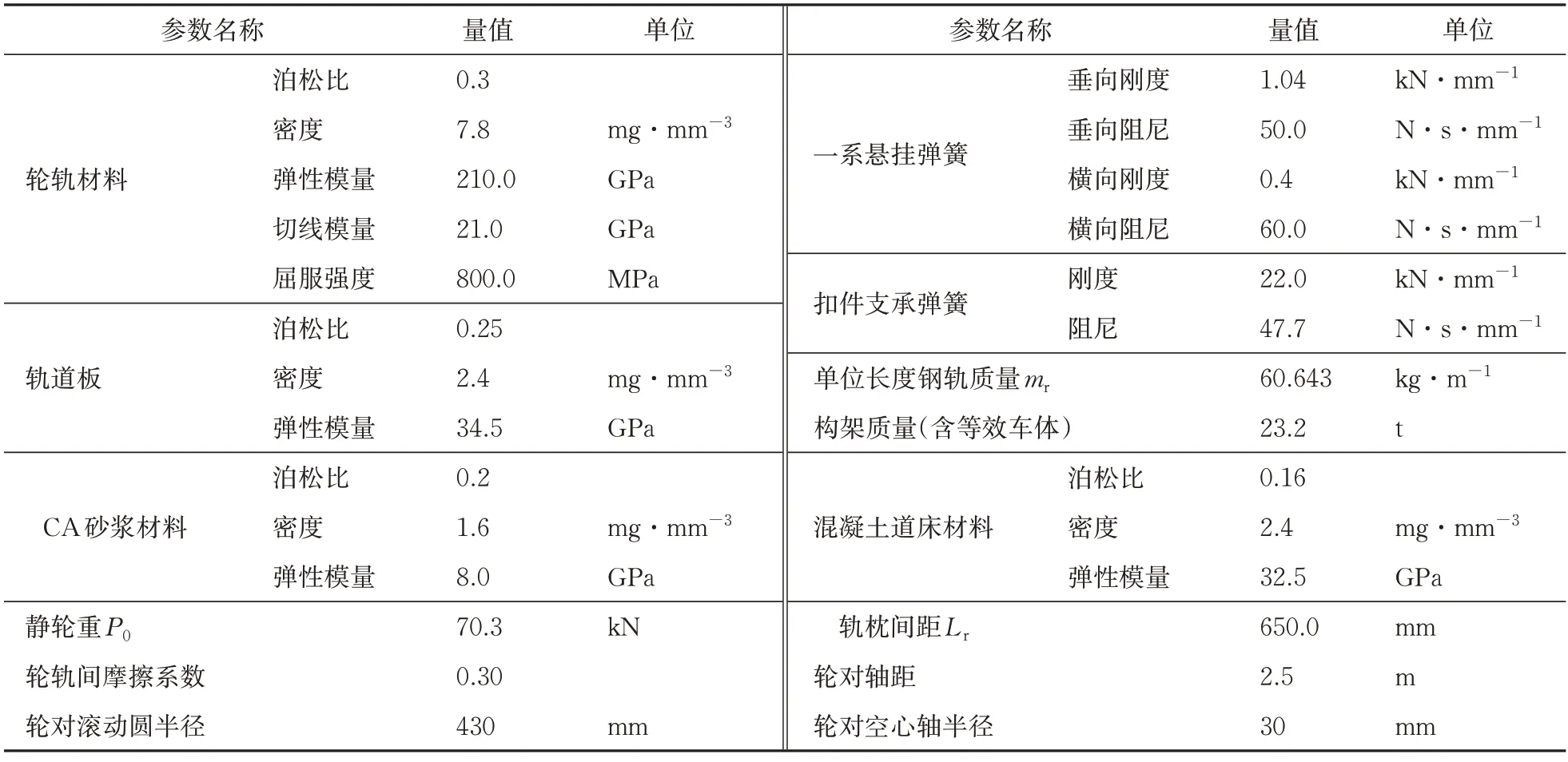
表1 轮轨动力学模型主要参数列表

1.3 模型验证

采用高速综合检测列车以300 km·h-1速度运行时在波磨区段的轴箱垂向振动加速度实测数据，验证图3所建模型的准确性。该波磨区段持续长度约20 m，30～300 mm 带通滤波后轨道不平顺及其频谱曲线如图7 所示。由图7 可知：波磨区段轨道不平顺幅值在±0.07 mm范围内波动；频谱曲线在空间频率12.46 m-1处存在能量集中，说明波磨主要的波长成分为80 mm，而其他波长成分所占比重较小。波磨现场复核时轨面状态如图7（b）右上侧照片所示，复核结果表明左股钢轨表面存在波长约为80 mm 的波磨，且由式（1）可知该波磨区段激励轴箱振动加速度的主频约为1 041.3 Hz。

图7 某波磨区段实测轨道不平顺数据

根据式（8），将图7（a）所示轨道不平顺施加到轮轨动力学模型，在300 km·h-1速度下轴箱垂向振动加速度仿真结果与实测数据时程曲线对比如图8（a）所示。图中：g为重力加速度；虚竖线左侧表示轴箱垂向振动加速度存在振幅约为±5g的周期性波动，是由轨枕对钢轨不连续支承作用引起的。由图8（a）可知：实测数据与仿真结果的时域波形均呈现由小增大再减小的拍振特征，幅值波动范围为±190g，仿真结果与实测数据在时域上幅值吻合良好、变化趋势一致。

仿真结果与实测数据经过时频转换技术［24］，得到其在频域上的分布特征如图8（b）和图8（c）所示。图中：颜色由蓝色到红色表征了轴箱垂向振动加速度能量依次增大。由图8（b）和图8（c）可知：仿真结果和实测数据在频域具有相似的分布特征；红色频段为轴箱垂向振动加速度最大能量所在的频段，约为1 041.3 Hz，与图7（b）所示波磨在300 km· h-1时的激励频率一致。

由图8 中实测轴箱振动加速度与仿真结果的时频域对比可知两者幅值相当，频域分布一致，验证了轮轨动力学模型仿真结果的正确性。

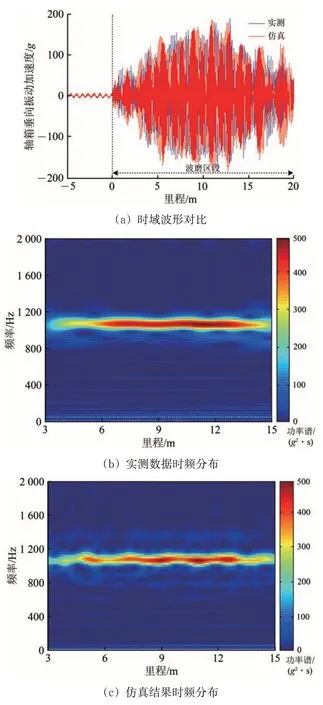
图8 轴箱垂向振动加速度时程波形和时频分布仿真与实测对比

2 波磨与轴箱垂向振动加速度映射关系

2.1 仿真步骤

绘制轴箱垂向振动加速度上包络线数据的累积概率分布曲线，以拉依达准则选取该曲线上99.73百分位数值记作A，并将其作为衡量波磨状态的表征量。

轴箱垂向振动加速度及其上包络线累积概率分布曲线及A值选取示意图如图9所示。图中：红色五角星对应的纵坐标值即为图7（b）所示波磨状态的表征量A。

图9 轴箱垂向振动加速度包络线及A值选取示意图

波磨的谷深值和波长均影响A值的大小，下文采用轮轨动力学模型研究300 km·h-1速度时波磨与A值之间的映射关系，从而推导得到估算波磨谷深值的表达式，采用的仿真步骤和数据处理方法等如下。

（1）建立轮轨动力学模型，根据仿真工况参数及式（8）在钢轨ab段上施加12 个整周期余弦型轨道不平顺，其中波磨起始位置点a与坐标原点o相距12 m。

（2）隐式计算重力载荷作用下轮轨动力学模型位移场，作为显式计算的初始边界状态。

（3）在轮对上施加运行速度和牵引扭矩载荷，仿真输出轮对经过钢轨波磨区段工况下的轴箱垂向振动加速度、运行距离等，输出频率为10 kHz。

（4）统计该工况下轴箱垂向振动加速度上包络线累积概率99.73百分位数，即A值。

（5）在钢轨ab区段上施加新的仿真工况，并按步骤（2）—步骤（4）统计新工况下波磨表征量A。

（6）按照步骤（5）依次计算所有工况下的波磨表征量A。

（7）拟合波磨波长、谷深值等参数与A值之间映射关系的函数表达式。

（8）由式（1）及轴箱垂向加速度主频计算波磨波长，得到A值与谷深值之间的关系式。

2.2 数值计算结果

谷深值较大时波磨与轴箱垂向振动响应之间不再是近似线性传递。为了厘清两者之间的对应关系，在仿真数值计算时谷深值取值范围较大而波长设置范围为40～180 mm。300 km·h-1车速下波磨波长为40，100 和180 mm，谷深值分别为0.02，0.06，0.10，0.14，0.18 和0.20 mm 时轴箱垂向振动加速度波形如图10所示。

图10 波长40，100和180 mm 不同谷深值时轴箱垂向振动加速度波形

由图10 可知：相同波长时轴箱垂向振动加速度波动范围均随着谷深值的增加而增大，但增大的幅度与波长有关，如谷深值由0.02 mm 增至0.20 mm 时40 mm 波长波磨激励的轴箱垂向振动加速度波动值由28.79g增至157.52g、增大约5.5 倍，100 mm波长的由41.04g增至240.30g、增大约5.8倍，100 mm 波长的由31.49g增至180.73g、增大约5.7 倍；100 mm 波长时，轴箱垂向振动加速度的波动范围明显比40 和180 mm 波长时大。因此，相同谷深值时不同波长的波磨激励A值也存在差异。

图10中3组波长条件下，A值随谷深值变化的柱状图如图11 所示。图中：虚线为谷深值与A值之间趋势线。

图11 波长40，100 和180 mm 时轴箱垂向振动加速度A 值统计结果

由图11 可知：相同谷深值时波磨表征量A值与波长关系较为复杂，但整体上在谷深值相同时100 mm 波长波磨激励的A值最大；在谷深值小于0.14 mm 时，40 mm 波长波磨激励的A值大于180 mm 波长时，而在谷深值大于0.14 mm 时，40 mm波长波磨激励的A值小于180 mm波长时。

当谷深值继续增加时，A值随谷深值变化的散点图如图12所示。

图12 不同波长条件下A值随谷深值变化散点图

由图12可知：3组波长条件下，均为谷深值较小时A值随谷深值近似线性增大，在谷深值较大时A值随谷深值增大变化趋于平缓。这是因为随着谷深值增加，轮轨在波谷附近发生脱离，接触位置集中在波峰附近，导致A值与谷深值关联性较弱。

在100 mm 波长、不同谷深值波磨激励下轮轨垂向力波形及对应的轮轨接触状态如图13 所示。图中：红色为轮轨脱离区，灰色为轮轨接触区。

图13 波长100 mm时轮轨垂向力及轮轨接触状态示意图

由图13 可知：谷深值小于0.20 mm 时，轮轨垂向力最小值均大于0 kN，轮轨不脱离接触；谷深值≥0.20 mm 时，轮轨垂向力最小值为0 kN，此时轮轨脱离接触，但脱离位置较少；谷深值增加到0.30 mm 时，轮轨垂向力为0 kN 的位置增多，轮轨脱离接触区域逐步扩大；谷深值≥0.50 mm时，轮轨垂向力为0 kN 的区域不再明显变化，相应地轮轨脱离接触位置的数量不再增加，说明此时轮轨脱离区域相对固定，不随谷深值的增加而明显改变；随着谷深值由0.10 mm 增加至0.90 mm，轮轨在波谷附近逐渐发生脱离而接触区集中在波峰附近。在车辆运行速度固定时，轮轨接触状态变化较小，导致波磨激励轴箱垂向加速度波动范围趋于平缓。

定义轨面变化率ξ为波磨谷深值与波长的比值，为

图12 中300 km·h-1速度下波磨波长为40，100 和180 mm 仿真工况下波磨表征量A值与轨面变化率ξ之间散点和拟合曲线如图14所示。

由图14可知：3组波长工况下A值整体上随着轨面变化率ξ的增加而增大，但A值增幅随ξ增加而变缓。

利用有理式和非线性最小二乘方法［32］拟合图14中A值与ξ之间的函数关系，得

图14 不同波长条件下波磨表征量A值与轨面变化率ξ散点和拟合曲线

式中：c1，c2和c3为待定拟合参数。

在拟合优度不小于0.995 时，40～180 mm 波长条件下拟合参数c1，c2和c3取值见表2。

表2 不同波长条件拟合参数取值

波磨程度轻微时轨面变化率ξ较小，由式（10）可知在ξ≈0 时A值近似等于拟合参数c2与c3的比值c2/c3，其值应接近于0g，波动范围如图8（a）虚线左侧未施加波磨时轴箱振动加速度仿真结果；波磨程度严重时轨面变化率ξ较大，由式（10）知ξ取值越大A值越趋近于拟合参数c1。拟合参数c1及比值c2/c3与波长之间关系如图15 所示。由图15 可知，拟合参数c1整体上随着波长增加而增大，在上下限虚线内波动；拟合参数c1上存在2个局部峰值点，其中局部峰值点ck1对应的波长范围为56～72 mm，局部峰值点ck2对应的波长范围为120～136 mm。局部峰值的产生与钢轨Pinned-Pinned共振频率fpp有关。

图15 拟合参数随波磨波长变化

钢轨Pinned-Pinned 共振是轨道振动驻波节点位于轨枕支承位置，n阶fpp计算式［33］为

式中：Lr为轨枕间距，0.65 m；mr为单位钢轨质量，60.643 kg· m-1；EI为钢轨抗弯刚度，6.62×106N· m2。

由式（11）可知，当n=1 时钢轨1 阶Pinned-Pinned 频率fpp约为1 227.8 Hz。图2 所示轮轨动力学模型中钢轨1阶Pinned-Pinned共振频率为1 215.1 Hz，与式（11）计算得到的数值较为接近，也验证了所建模型数值计算的准确性。

速度为300 km·h-1时，由式（1）可知图15（a）中局部峰值点所在60～72 和120～136 mm 波长波磨引起轮轨振动的激励频率对应为1 157.4～1 388.9 和612.7～694.4 Hz，该频带接近图3 中钢轨1 阶Pinned-Pinned 共振频率及其半频，是造成拟合参数c1曲线上局部偏大的原因。图15 中Ck1和Ck2对应频段附近钢轨的模态振型如图16所示。

图16 钢轨模型的振动模态振型

3 谷深值估算

由图12 及图14 可知，A表征了波磨激励轴箱垂向振动的程度但与波磨特征参数不存在对应关系。式（10）揭示了A与轨面变化率ξ之间的映射关系并分析了拟合参数物理特性。在波磨波长估算基础上可利用A值估算谷深值，由式（10）可知

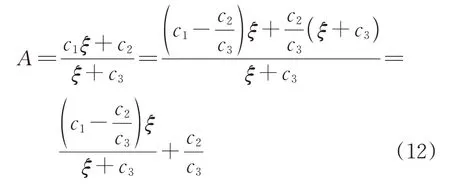
我国高铁线路对波磨谷深值管理较为严格，轨面变化率ξ值较小。由图15（b）可知此时拟合参数c2/c3的取值近似等于0，式（12）可写为

联合式（9）可得由A及波长λ估算波磨谷深值的估算值的计算式为

由式（15）可知第i个波长成分对应的谷深估计值为

式中：i为波长个数；c1，i和c3，i为波磨表征量Ai与波长λi之间的拟合参数。

波磨区段波长成分及对应的谷深值均较多，在应用式（17）计算时仅考虑有限个波长成分结果，即m取值满足下式

前述表2 给出了300 km·h-1时部分波长条件下A与ξ之间的拟合参数，40～180 mm范围内其他波长对应的拟合参数可通过表2中结果插值得到。

4 方法验证

由图17 可知：50 组对比样本中大部分散点集中在虚线d=附近，两者均方误差约为22 μm，相关系数约为0.95，说明两者数值上较为接近且存在较强的线性相关性。在大于0.08 mm时两者之间均方误差约为16 μm，此时说明采用轴箱垂向振动加速度及式（17）的估算结果精度进一步提高。

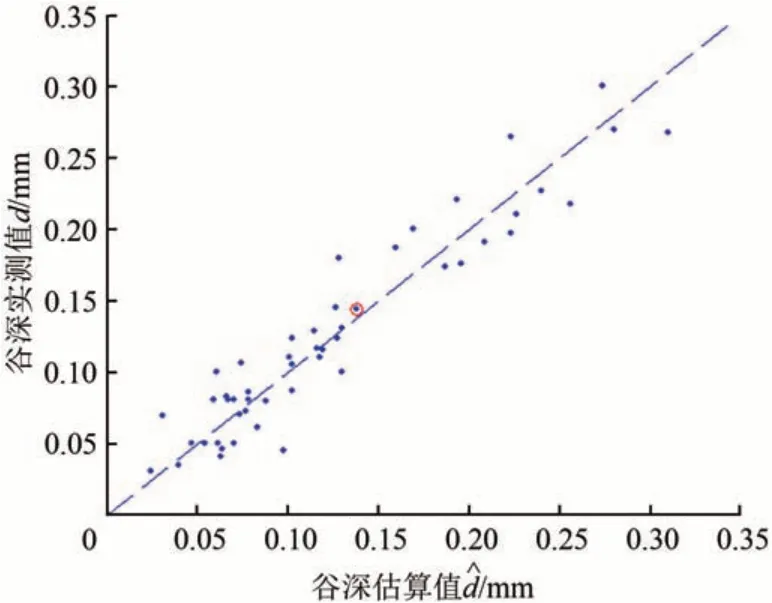
图17 50组波磨谷深值与谷深估算值关系

采用误判率Ep分析式（17）所得谷深估算值用于辅助波磨整治决策的可行性，误判率Ep越小表明式（17）的实用性越强，为

高速铁路无砟轨道线路维修规则［10］规定了波磨整治限值为谷深值d大于0.08 mm。因此，式（19）中p取0.08 mm，由图16 所示50 组对比数据及式（17）和式（19）得到的谷深估算值辅助波磨整治决策时的误判率E0.08为9.73%。而当p为0.07 mm 时误判率E0.07为2.97%，谷深限度值的适当降低有助于减少波磨误判的风险，因此在轴箱垂向振动加速度评价波磨状态时建议选取大于0.07 mm作为上道复核预警值。

5 结论

（1）在波长不变时波磨激励的轴箱垂向振动加速度随着谷深值增大而非线性增大。在谷深值较大时，轮轨在波谷位置发生脱离，轮轨接触区域趋于波峰附近，轴箱垂向振动加速度随谷深值的变化较小且逐渐接近某一定值；在谷深值不变时，受轨道固有振动模态的影响轴箱垂向振动加速度与波磨波长之间映射关系较为复杂，因此在评价波磨状态时应重点考虑波长对轴箱垂向振动加速度幅值的影响。

（2）在拟合优度大于0.995 时，采用非线性最小二乘法及有理式方程得到轴箱垂向振动加速度99.73 百分位数与轨面变化率之间函数曲线。拟合参数c1的物理意义为该波长条件下轴箱垂向振动加速度的最大趋近值。受钢轨Pinned-Pinned 振动模态的影响，c1值在部分波长上呈现局部峰值特征，在300 km·h-1时受钢轨Pinned-Pinned共振频率及其半值影响较大的波长范围分别为60～72 和120～136 mm。

（3）利用轴箱垂向振动加速度能量主频及车辆运行速度估算波磨主要成分的波长，在此基础上推导了谷深估算值计算式。该方法在高铁线路波磨状态监测中得到试用，结果表明：实测谷深值与谷深估算值之间相关系数为0.95 时均方误差为0.022 mm。说明两者具有较强的相关性和较小数值误差。采用谷深估算值辅助打磨整治决策时误判率E0.08约为9.73%，E0.07小于3%。为降低波磨状态的漏判，在轴箱垂向振动加速度评价轨道状态时建议选取谷深估算值大于0.07 mm 作为上道复核预警值。

（4）我国高铁线路、车辆型式和运营条件复杂多样，而轴箱振动加速度受到轨道几何不平顺、轮轨匹配、车轮不圆顺度、测试精度、信号信噪比等多种因素影响，研究结果数据主要来自高速综合检测列车特定工装下的测试数据，下一步结合实践应用和仿真技术研究不同轨道类型和车辆型式组合下轴箱垂向振动加速度与波磨谷深值之间的映射规律，进而丰富和完善基于轴箱垂向振动加速度评价钢轨波磨状态的方法。