基于试验和数值仿真的软土群桩基础m值研究

宋旭明，王天良，唐 冕，潘鹏宇，程丽娟

（1.中南大学 土木工程学院，湖南 长沙 410075；2.湖南省交通规划勘察设计院有限公司，湖南 长沙 410200）

我国东部沿海地区经济发展迅速，基础设施建设规模庞大，高速铁路网日益密布。该区域分布着大范围承载力较小、工程性质较差的软土，而高铁桥梁对桥墩刚度又有较高的要求。针对不同结构形式的铁路桥梁，《铁路无缝线路设计规范》［1］给出了其墩台顶最小纵向水平线刚度的限值。目前采用文克尔弹性地基梁模型进行桥墩设计时，多选用m法计算土的地基系数。

m法是迄今为止世界上运用最为广泛的计算方法，王唤龙等［2］采用常数法、m法和k法，推导了受压微型桩屈曲临界荷载的理论计算公式，进而导出压杆计算长度系数。蔺鹏臻等［3］基于m 法，建立了考虑边坡效应的桩基础静力微分方程，分析边坡效应对桩基位移、弯矩、剪力和桩侧土压力的影响规律。m法的关键是合理确定地基系数的比例系数m值。

众多学者针对m值进行了研究。周万清等［4］对珠海软土地基中2 根细长PHC 管桩进行水平荷载试验，得到了PHC 管桩基础m值。屈希峰［5］通过单桩静载试验并利用有限元软件ANSYS 模拟桩土之间的相互作用，得出了湿陷性黄土的m值。范秋雁等［6］对原状泥质软岩样本进行了室内试验，并利用有限元软件进行模拟，给出了泥质软岩的m值取值范围。黄晓亮等［7］对软土区3 根组合桩进行试验研究和计算分析，给出了其m值的计算方法。楼晓明等［8］利用p-y曲线法与m 法，建立了饱和黏性土m值与地基不排水抗剪强度和桩径等指标的关系。徐中华等［9］结合反分析软件UCODE和有限元软件ABAQUS，提出了一种依靠围护墙实测变形来反演基坑土体m值的方法。丁梓涵等［10］通过试验发现地基土强度增大将显著提高单桩水平承载力与m值。尹平保等［11］通过室内模型试验测得了不同斜坡坡度及水平荷载作用下的m值，建立了斜坡土体m值同桩身水平位移、斜坡坡度和水平荷载之间的拟合关系。李晓明等［12］提出陡峻边坡碎石土、碎石土-基岩场地的m值估算公式，并给出了修正系数。康银庚等［13］通过3 根灌注桩的水平静载荷试验，得到了硅藻土区m值。

采用试验方法确定m值时，需要根据结构的荷载位移曲线进行反算，结构形式、群桩效应都会对试验结果产生影响，使得不同工况下计算的m值不尽相同。目前对于土体m值的确定已有较多研究，但大多针对单桩、防护桩、围护墙等结构，关于群桩基础m值的研究较少，尤其是对于软土地区高铁桥梁群桩基础m值的研究。m值是影响桥墩刚度设计的重要参数，根据《铁路桥涵地基和基础设计规范》［14］，结构在地面处水平位移6 mm时，对于流塑黏性土、淤泥等软土，m值可取3 000～5 000 kN·m-4，但取值范围较大，设计时如何合理取值难以把握。

本文依托江苏南沿江城际铁路工程，根据现场试验及规范改进了群桩基础m值的反演方法，结合数值仿真，得到该场区m值的合理取值，并验证《铁路桥涵地基和基础设计规范》中m值的适用性。本文的研究可为软土地区m值取值提供依据，促进相关设计及施工规范的修正，计算方法也可供其他场区m值的确定借鉴参考。

1 m值反演方法

《铁路桥涵地基和基础设计规范》附录D 给出了由m值，桩的水平变形系数，桩身抗弯刚度及计算宽度，承台底水平位移、转角，墩台顶至承台底的距离求得承台顶水平位移的计算公式。通过群桩水平静载试验，获得荷载-承台顶位移曲线，可利用规范中的计算公式反演m值。

由于规范给出的承台顶水平位移与m值的关系表达式复杂，直接反算m值比较繁琐，本文对张蕾等［15］提出的假定m值、通过桩顶水平位移试算m值的方法进行改进。反演方法具体步骤如下。

（1）参考《铁路桥涵地基和基础设计规范》给定m值的初始值m1，给定计算次数上限值n。

（2）将第i次计算得到的m值mi（i=1，2，…，n）代入群桩计算公式，求得第i次计算的承台顶位移xi。

（3）按下式计算相对误差

式中：εi为第i次计算的相对误差；xi为第i次计算得到的承台顶位移，mm；x0为群桩水平静载试验得到的承台顶位移，mm。

（4）判断承台顶位移计算相对误差是否满足要求。若相对误差不大于误差限值εl，即εi≤εl，则结束计算，第i次计算采用的mi即为反演得到的m值。若εi>εl，则借鉴Runge-Kutta 原理［16］求解mi+1

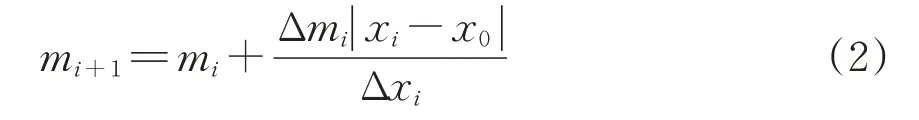
式中：Δmi为第i次赋予的变化量，本文取1‰mi，kN·m-4；Δxi为根据群桩计算公式得到的Δmi所对应的承台顶位移变化量，mm。

（5）重复步骤（2）—步骤（4），直至相对误差满足要求或达到计算次数i的上限值1 000，输出m值。

2 群桩水平静载试验

2.1 试验工点

选取江苏南沿江城际铁路常州至太仓段白茆河特大桥31#—33#墩的群桩基础作为本文的试验对象。该区段桥跨32 m，结构参数见表1。工点立面和平面布置如图1所示。

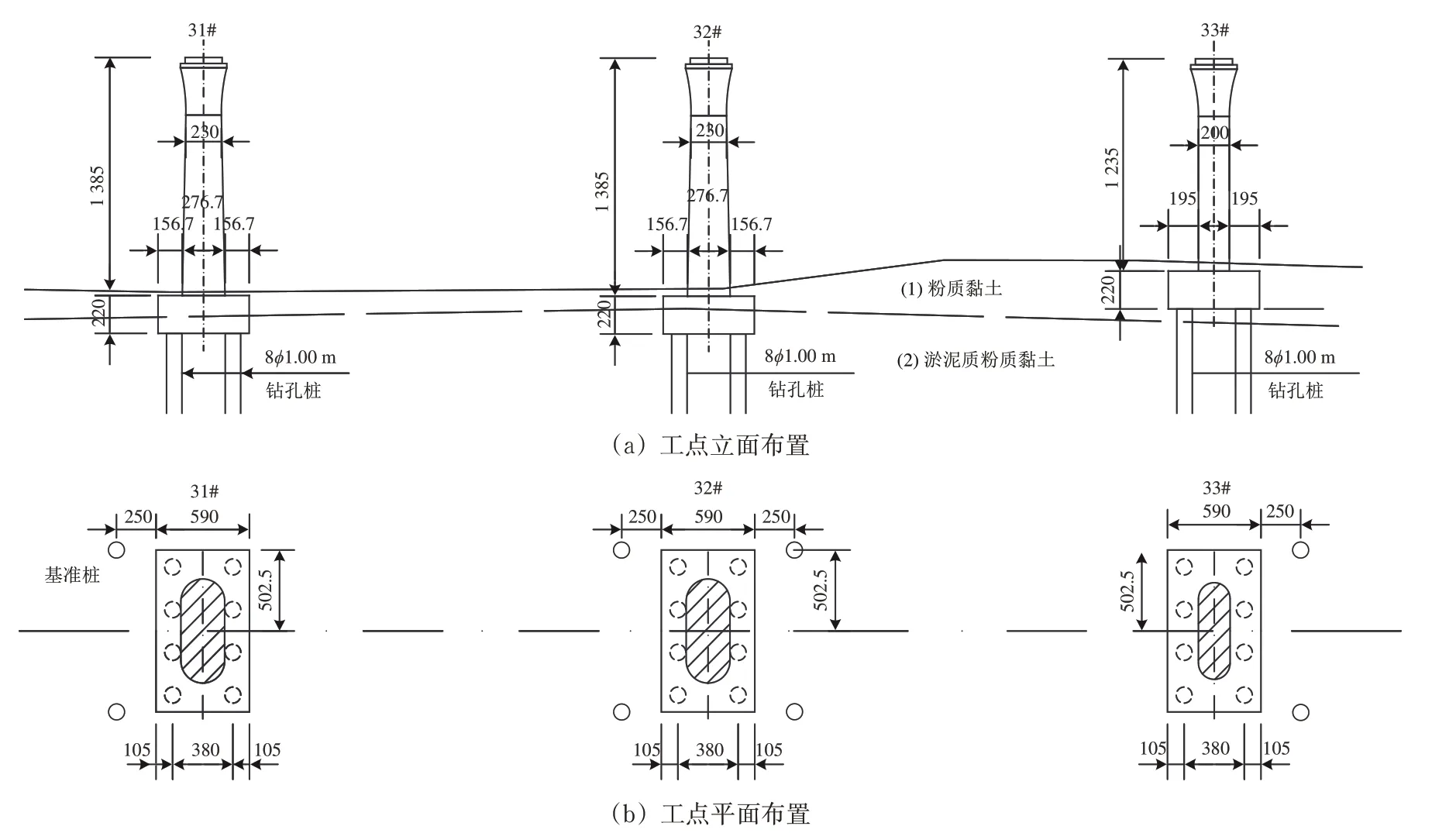
图1 试验工点（单位：cm）

表1 结构参数

试验场地地基土自上而下分别为粉质黏土、淤泥质粉质黏土、粉质黏土、粉质黏土、粉土、粉砂、细砂、粉质黏土夹薄层粉砂、粉砂和细砂。当基础侧面为多种不同土层时，应将地面以下hm深度内的各层土换算成一个m值，作为基础整个深度h内的m值。hm可由下式求得

式中：d为桩径，m。

本试验中d为1 m，求得hm为4 m。hm深度内的各土层如下。

（1）粉质黏土：灰色、灰黄色，软塑，层面标高0.11～4.2 m，层厚0.8～6.8 m，平均厚度2.67 m。

（2）淤泥质粉质黏土：灰色，流塑，层面标高-15.48～3.04 m，层厚1.4～27.0 m，平均厚度8.92 m。

其力学基本参数见表2。

表2 hm深度内土层力学基本参数

2.2 试验方法

通过群桩基础之间的对拉，分别对31#—32#群桩和32#—33#群桩进行水平静载试验。加载方式采用慢速维持荷载法，分别在31#和32#墩标高2.5 m 处、32#和33#墩标高3.8 m 处预留加载孔，通过千斤顶张拉钢绞线实现对桥墩的水平加载。

测试方法参照《建筑基桩检测技术规范》［17］。在张拉段和锚固段分别放置测力传感器测量拉力。在承台顶和承台底各安装2 只百分表，测量承台水平位移。每级荷载施加后，在5，15，30，45 和60 min时记录百分表读数，以后每隔30 min测读一次。每一小时内百分表读数不超过0.1 mm 视为稳定，施加下一级荷载。31#—32#群桩测试装置布置如图2所示，群桩水平静载试验现场如图3所示。

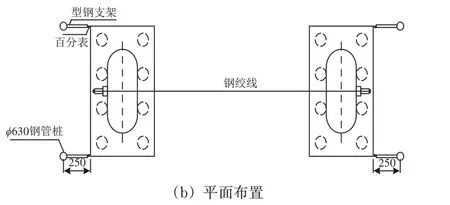
图2 31#—32#群桩基础测试装置布置示意图（单位：cm）

图3 群桩试验现场

2.3 试验结果

采用慢速维持荷载法进行试验，分级荷载见表3。其中，对32#—33#群桩进行了重复试验，于首次试验卸载完成的两天后进行，分别用“一次”“二次”表示首次试验和重复试验。考虑到本次试验对工程桩进行加载，不能影响结构的正常使用，加载时承台顶水平位移均未超过1.6 mm。

表3 水平静载试验分级荷载 kN

图4为群桩基础的荷载-位移曲线，32#（32#—33#）表示32#—33#群桩对拉试验中的32#群桩基础，后文表示方法均与此相同。采用本文提出的反演方法，计算各级荷载下的m值，可得到群桩基础m值-位移曲线，如图5所示。图5 中，对32#—33#群桩的一次试验和二次试验结果进行并置拟合。

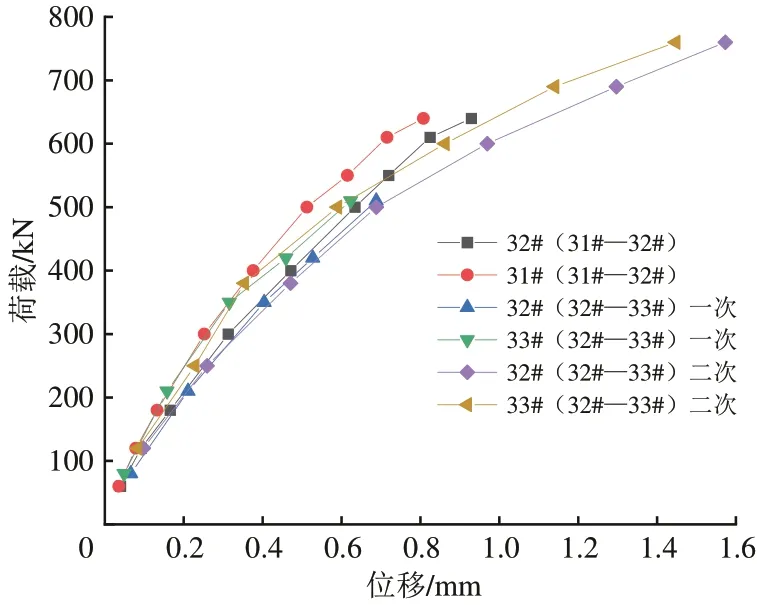
图4 荷载--位移曲线（现场试验）

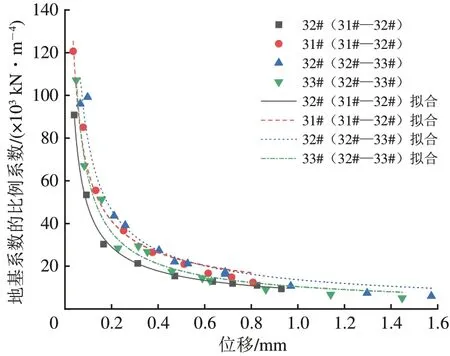
图5 m值-位移曲线（现场试验）

由图4 和图5 可知：荷载与位移呈非线性关系，随荷载增加，桩侧土的位移梯度逐渐增大，m值也随之降低，与《建筑桩基技术规范》［18］中的描述一致；m值与位移呈非线性关系，小位移下m值较高。

已有文献表明［19-21］，在水平荷载的作用下，即便桩基只发生较小位移，土体也会表现出较强的非线性，且大位移下的m值随桩在地面处位移增大而呈幂函数衰减。对本文试验得到的群桩基础m值-位移曲线采用幂函数进行拟合

式中：a和b为拟合参数；x为承台顶（结构地面处）水平位移，mm。

拟合得到相关参数见表4。表中，群桩基础m值是指承台顶水平位移6 mm 时的试验外推值。由表4 可知：不同群桩基础得到的m值最小值为2 615 kN·m-4，因此偏保守给出该地层条件下的群桩基础m值为2 600 kN· m-4。需注意的是，《铁路桥涵地基和基础设计规范》中给出的软土地区m值的下限为3 000 kN·m-4，该值大于本次试验所得m值。因此，如按规范取m值，该工点桥墩的计算刚度偏大。

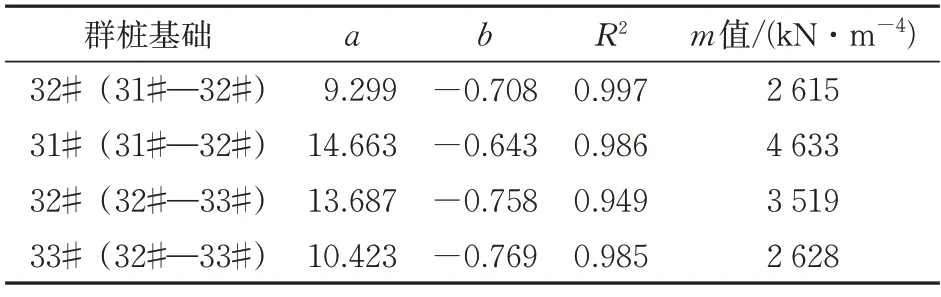
表4 群桩基础m值--位移曲线拟合参数（现场试验）

3 数值仿真

3.1 数值模型

采用有限元软件Midas GTS 对上述群桩水平静载试验进行数值仿真，计算分析群桩基础m值随承台顶水平位移的变化规律。

数值模型如图6 所示。其中，X正向指向南沿江城铁大里程方向，Z正向指向为铅锤向上。X，Y和Z方向长度分别为115，80 和135 m。桥墩、承台、土体采用混合实体单元模拟，桩基础采用梁单元模拟，桩土间相互作用采用桩界面单元进行模拟。对于混凝土构件，采用弹性本构关系进行分析计算；对于土层，考虑软土受到大于屈服应力时的外荷载发生的塑性变形，采用修正剑桥本构关系进行分析计算。模型的边界条件为顶面为自由面，两侧水平约束，底面取竖向和水平向约束。综合考虑计算精度和计算效率，土体的网格尺寸取2 m，桥墩、承台网格尺寸取1 m，桩基梁单元长度为0.5 m，共计163 168单元，166 966节点。

图6 数值模型

3.2 参数标定

为保证有限元模型可合理反映试验结果，需进行土体参数的标定。在参数标定前需进行敏感性分析，将敏感度较小的参数取为常量，以保证计算的效率及结果的合理准确。

根据文献［22］，Midas GTS 修正剑桥模型中4 个参数对位移的计算影响较大，即正常固结线坡度λ、超固结线坡度κ、临界状态线斜率M、泊松比ν。参考工点土工试验数据和相关文献［22-23］对参数进行取值，见表5。

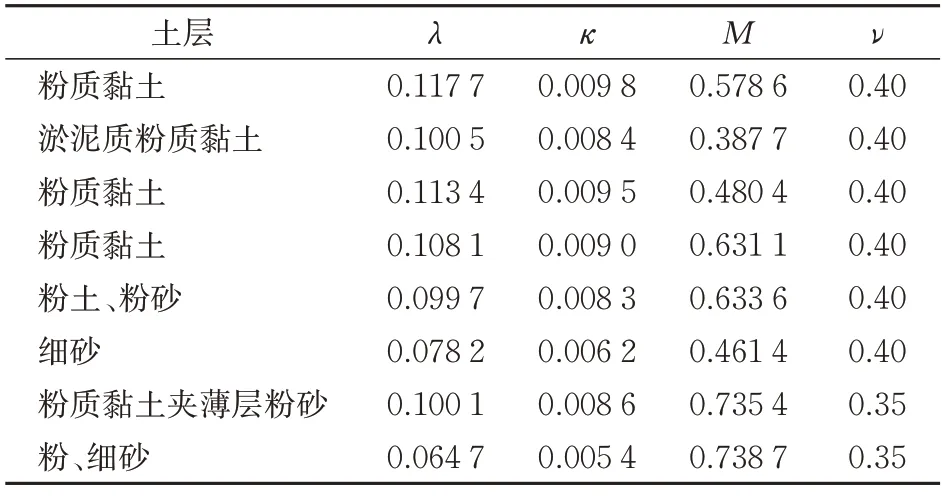
表5 模型参数

定义参数的敏感性系数f为

式中：y*为修正剑桥各参数λ，κ，M和ν的基准值；Δy为对y*赋予的变化量，本文取1%y*；S*为承台顶位移基准值，mm；ΔS为由Δy产生的模型中承台顶位移变化量，mm。

采用控制变量法，分别以31#和32#群桩基础承台顶位移为基准值，根据式（5）计算本文数值模型的参数敏感性系数，结果见表6。

表6 数值模型的参数敏感性系数

由表6 可知：参数κ和ν是对位移计算结果影响较大的参数，重点对其进行标定；参数λ和M对位移的影响较小，可将其取为常量。

参数标定流程如图7 所示。考虑到试验过程中小荷载下，位移测量结果易受施工质量，试验场地周围行车干扰等其他原因干扰，兼顾计算效率，将目标函数取为最后一级荷载下各承台顶位移实测值与计算值之差。参考徐中华等［9］寻求参数最优解的方法进行迭代计算并判断是否满足收敛准则。

图7 参数标定流程图

计算过程中，构建的目标函数F为

式中：n为承台顶位移实测值总数，n取2；Si*为第i个承台顶位移实测值，mm；Si为第i个承台顶位移计算值，mm。

标定后的各土层κ和ν取值见表7。采用标定后参数进行数值仿真，得到群桩基础荷载-位移曲线，并与试验曲线进行对比，如图8所示。

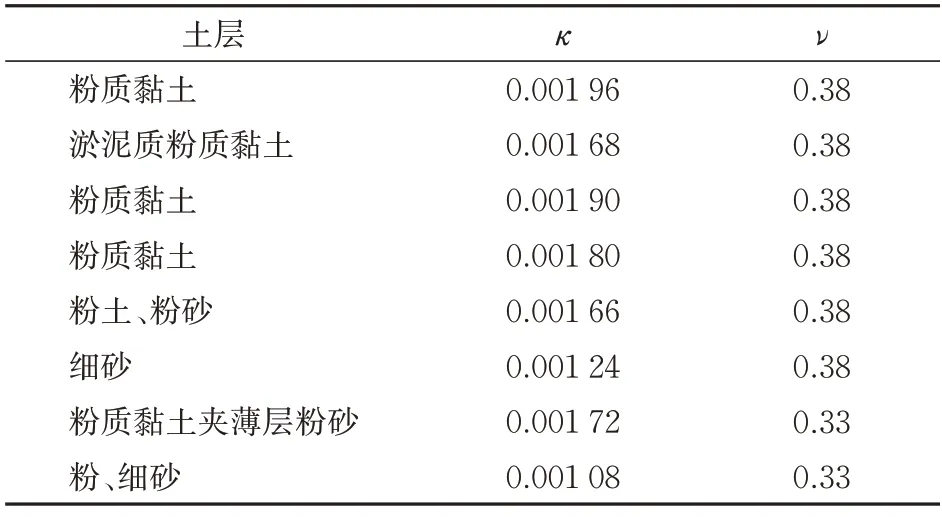
表7 修正剑桥模型的标定参数值

由图8 可知：荷载较小时，位移计算值与实测值相差较大，但随荷载增加二者差值逐渐减小，最后一级荷载下，计算结果相对误差为1.0%～13.6%，表明有限元模型可较好地反映群桩基础受力变形特性。

图8 现场试验与数值仿真的荷载--位移曲线对比

3.3 计算结果

为了使承台顶水平位移达到6 mm，在有限元计算中加大荷载数值到3 200 kN，得到群桩基础荷载-位移曲线如图9所示。由图9可知：数值仿真得出的荷载与位移仍表现为非线性关系，荷载越大，桩侧土的位移梯度越大，与试验得出的荷载位移关系规律一致。

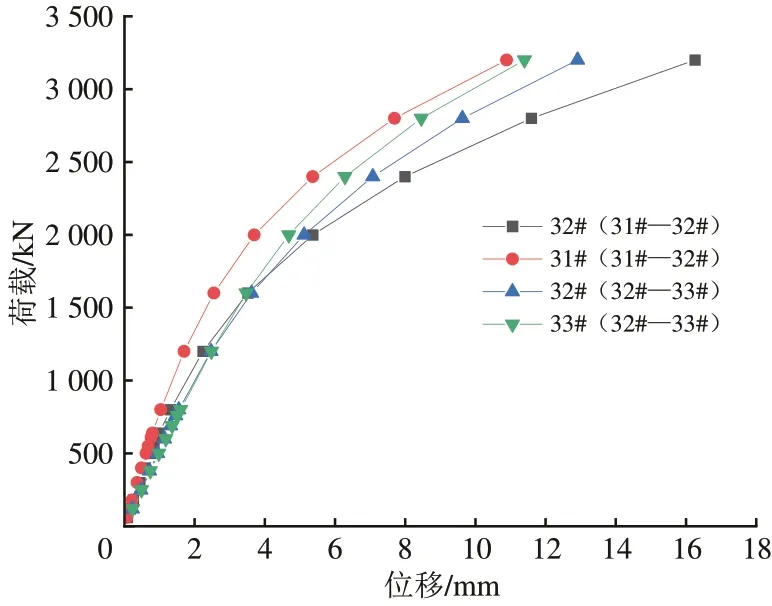
图9 荷载--位移曲线（数值仿真）

采用本文提出的反演方法，计算各级荷载下的m值，得到群桩基础m值-位移曲线，并采用公式（4）对其进行拟合，如图10 所示。拟合得到的相关参数见表8。

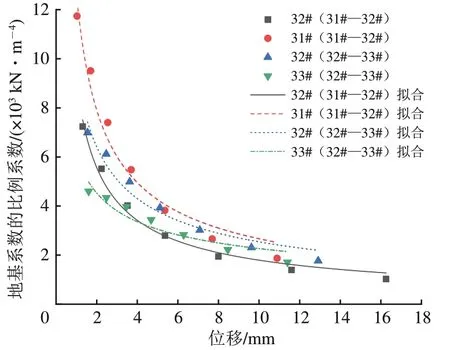
图10 m值-位移曲线（数值仿真）

表8 群桩基础m值-位移曲线拟合参数（数值仿真）

综合图10和表8可知：数值仿真所得群桩基础m值的最小值为2 570 kN·m-4，与试验曲线外推得到的群桩基础m值2 600 kN·m-4基本一致，相对误差1.15%；与试验得到的m值-位移拟合曲线相比，拟合参数a取值相差2.44%，b取值相差0.56%，二者基本一致。由以上分析可知，本文数值仿真参数取值合理，计算结果可靠，可为实际工程提供参考。因此，对于没有条件进行水平荷载试验确定m值的工点，建议选择合理的土体本构模型和参数进行数值仿真，并综合规范取值，以获得比较合理的群桩基础m值的建议值。

需注意的是，试验和数值仿真的m值计算结果均小于《铁路桥涵地基和基础设计规范》给定的软土地区m值下限3 000 kN·m-4，本文研究结果可为相关设计及施工规范的修正提供参考。

4 结论

（1）群桩水平静载试验结果表明，m值随承台顶位移增加而降低，可采用幂函数m(x)=axb拟合，参数a取值范围9.299～14.663，参数b取值范围-0.769～-0.643。

（2）根据m值-承台顶位移拟合公式，承台顶位移为6 mm 时，该场区群桩基础的m值为2 600 kN· m－4，较规范建议偏小。

（3）数值仿真所得m值-承台顶位移曲线与试验结果基本吻合，说明模型参数取值合理、计算结果可靠。因此对于没有条件采用试验确定m值的工点，可采用数值仿真并综合考虑规范建议取值来获得合理的群桩基础m值。