面向接触网状态监测的无线传感网络循环冗余校验多项式性能研究

谭 平，毛江峰，丁 进，程剑锋，赵 阳，强 力，马吉恩

（1.浙江科技学院 自动化与电气工程学院，浙江 杭州 310023；2.中国铁道科学研究院集团有限公司 通信信号研究所，北京 海淀 100081；3.中铁高铁电气装备股份有限公司 研究中心，陕西 宝鸡 721013；4.浙江大学 电气工程学院，浙江 杭州 310027)

接触网是高速铁路的关键系统，是高速列车的动力之源，实现接触网状态在线监测，对保障高速铁路行车安全，提升高速铁路运营效率具有非常重要的意义。面向高速铁路接触网监测的无线传感网络节点，具有安装方便、布线简单、维护方便等优势，是今后技术发展的重要方向［1-2］。接触网状态在线监测无线传感模块需要满足五年以上的长寿命周期要求，但高速铁路沿线无线通信系统种类繁多、电磁环境复杂，如何保证无线链路中数据传输的可靠性和节点的能量消耗是十分关键的问题，因此合理设计用于接触网在线监测的无线传感模块通信协议，以及无线传感模块传输数据包的可靠性校验都极其重要。较差错控制编码方式而言，CRC编码方式对于均衡能量消耗和误码率问题都不失为1 种较好的解决方案，但从充分保障无线传输数据的完整性与可靠性的角度，还需要继续研究CRC的特征多项式性能，以确保选择的特征多项式位数合适、运算空间低，从而进一步提升校验性能。

目前CRC 算法主要通过串、并行算法或查表法实现。如罗宇等［3］将CRC 算法变为矩阵线性运算，降低运算耗时、节省资源占用。陈容等［4］和左飞飞等［5］分别提出基于递推法32 位改进并行算法，大大节省了硬件资源。王宁平等［6］对查表法进行优化，在1 个周期内实现CRC 运算。上述方法主要从编译码算法实现角度，根据实际情况兼顾软硬件配置，提高了CRC 算法的校验效率，但其应用范围均有一定局限性。

从自身性能来看，CRC的残余误差概率（RP）会直接影响校验结果。如16 位国际通用特征多项式CRC-ANSI 和CRC-CCITT，在17 位突发差错时的纠错率均为99.997%、18 位及以上时均为99.998%［7］。特征多项式校验时不同数据长度会出现不同残余误差概率［8］，分析特征多项式性能因素对校验特征多项式选取具有指导意义，其残余误差概率的计算结果也具有普遍适用性。Agarwal V K 等［9］推导得到关于残余误差概率合法码码重的计算方法。IEC 61784-3［10］给出残余误差概率的简化计算方法。KOOPMAN P等［11］通过最小汉明距离计算残余误差概率的方法来选取特征多项式，发现近似性能特征多项式无法运用简化模型计算并直接比较出校验性能，若直接运用原理法计算则步骤复杂、计算量大［6-7］。

目前CRC 特征多项式的性能理论分析不够充分，既有文献尚未形成可快速、准确选取性能更优特征多项式的统一标准。针对这一情况，本文首先建立特征多项式残余误差概率计算模型，根据特征多项式自身性能剖析影响残余误差概率的主要因素，提出1 种对任意数据长度校验实现CRC 多项式性能定量评估的计算方法。以设计接触网在线监测无线传感模块数据包256 bit 的数据位长为验证对象，先确认特征多项式位数，根据残余误差概率初步分析特征多项式性能，再通过对近似性能多项式位出错漏检率的精确计算，最终快速、准确选取更优检错性能特征多项式。

1 残余误差概率计算

残余误差概率也称为未被检测错误概率（Un⁃detected Error Probability，Pue）［12］。以k为数据码中待校验信息码的位长，r为校验位长，那么含校验位的数据总位长n=k+r。当CRC 多项式校验数据的位长不小于固有长度的2r-1-1 时，此时Pue值与生成特征多项式的选择无关，只与该特征多项式的最高阶数r有关；当待校验数据位长小于固定长度2r-1-1 时，校验码即为缩短码，此时Pue值既与特征多项式有关，又与缩短后的数据总位长n有关。根据文献［8］，Pue的通用计算方法有式（1）和式（2）这2种。

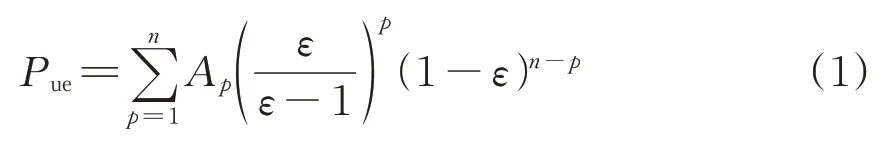
式中：Ap为合法码字中码重为p的码字数目，p=0，1，…，n；ε为位出错概率。

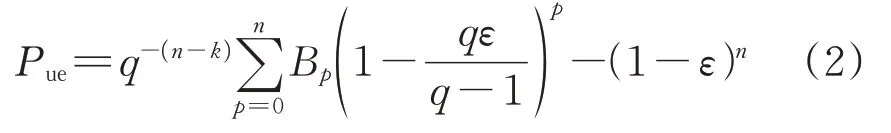
式中：q为有限域元素个数；Bp为合法对偶码中码重为p的码字数目，p=0，1，…，n。

以二进制对称信道（BSC）作为一般的信道编码模型，式（1）和式（2）分别对应为式（3）和式（4）。

1.1 残余误差概率序列计算方法

校验位长r越多，特征多项式校验能力越强。但随着待检数据总位长n增加，Ap和Bp的计算复杂度也会随之增加。在校验应用的众多场合中，一般r≪k，因此Bp的计算复杂度远小于Ap［13］，通过Bp计算残余误差概率更为简便。

以p（x）为不可再被约分的本原多项式，可针对Bp提出1种适用于校验码为固有长度或缩短码的计算方法，生成形式为“（x+1）p（x）”的多项式g（x），该方法具体步骤如下。

1）初始化数列

设有数列Wi（i=0，1，…，n），初始值为：W0取1，数列中其他项均取0。

2）生成特征序列

根据线性反馈移位寄存器，生成周期2r-1-1的序列。r-1 级线性反馈移位寄存器运算过程如图1 所示，主要由移位寄存器和异或门逻辑组成。图中：白、黑箭头分别表示数字流的运行方向和反馈移位寄存器的运算方向。

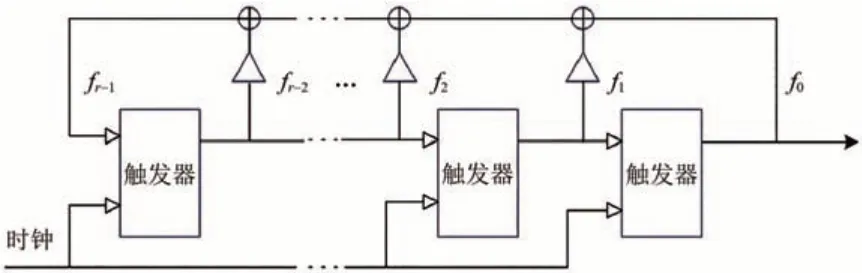
图1 r-1级线性反馈移位寄存器运算过程

线性反馈移位寄存器的周期即所产生的码组长度只与反馈方式有关。根据反馈方式，图1中的线性反馈移位寄存器对应的特征方程为［14］

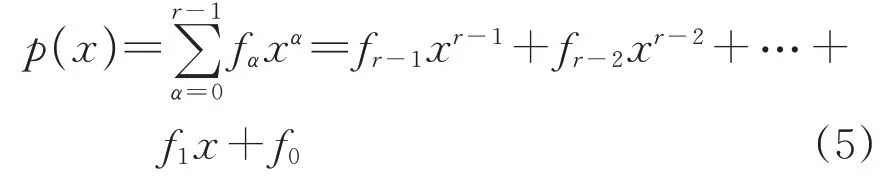
式中：α为第α位寄存器，α∈［0，r-1］；fα为0-1变量，若第α位寄存器参与异或运算，则取值为1，否则取值为0。

此特征方程即为生成的特征多项式g（x）=（x+1）p（x）中的本原多项式p（x）。

对各触发器赋初始值，且至少1 个触发器的初始值赋为1（若初始状态全为0则无法循环）。定义T时刻的输出aT是前一时刻状态sT-1=(aT-1aT-2…aT-n)和特征多项式系数矩阵f=(f0f1…fr-1)的转置矩阵的内积，即

直到下一循环周期开始前，依次记下这一周期内的全部输出，即为特征序列。

3）计算Wi

从特征序列最低位开始的n位进行检验，若从低位开始的n位中有i个1，则对应的Wi须加1。

先将生成的多项式左移1 位，即特征序列的初始最高位移到初始最低位；再检验特征序列新的最低n位，可按式（3）运用简化计算方法实现；重复上述检验步骤，直到特征序列初始最低位从序列最高位移出序列并恢复至初始状态。

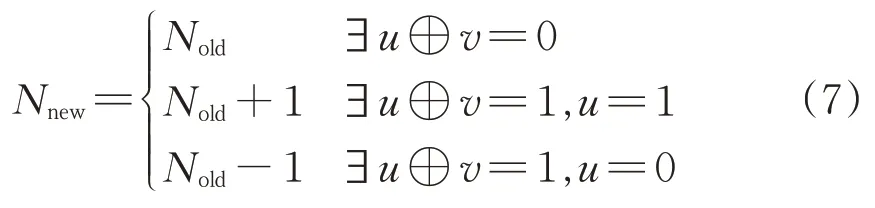
式中：Nold和Nnew分别为每次移位前、移位后最低n位中数字“1”的个数；u为特征序列每次移位前最低位；v为特征序列移位后的第n位。

4）计算Bp，得到残余误差概率后计算结束

Bp的计算式为

若n为偶数，则其中Wi自动相加；再将Bp代入式（4），就可以得到相应残余误差概率Pue的值。

1.2 残余误差概率比较

以8 位特征多项式CRC-8，16 位特征多项式CRC-CCITT，32 位特征多项式CRC-32Q 为例，目前国际通用的几种含x+1 因式的CRC 多项式分解计算方法分别如下［15］。3种计算方法得到的特征多项式都由因式x+1和p（x）组成。

1）8位特征多项式CRC-8

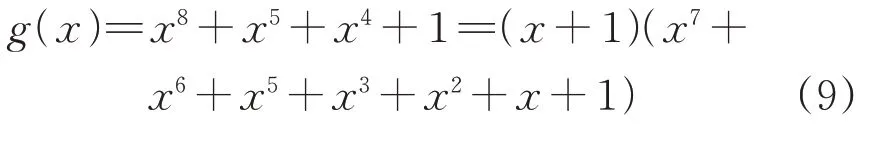
其中，

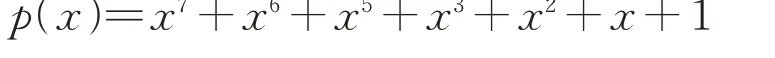
2）16位特征多项式CRC-CCITT

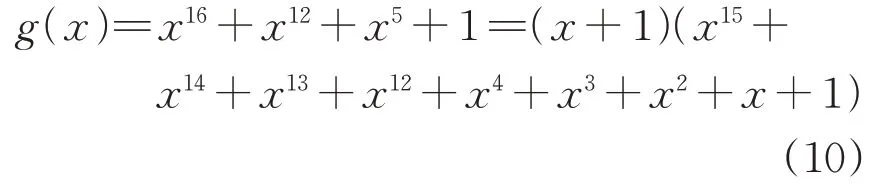
其中，

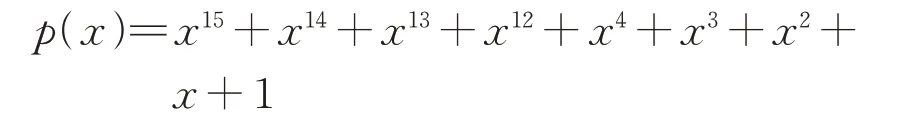
3）32位特征多项式CRC-32Q

其中，

对于接触网状态监测无线传感模块拟设计256 bit 待校验数据位，3 种计算方法下，计算得到的CRC 多项式残余误差概率结果如仿真软件截图如图2所示。

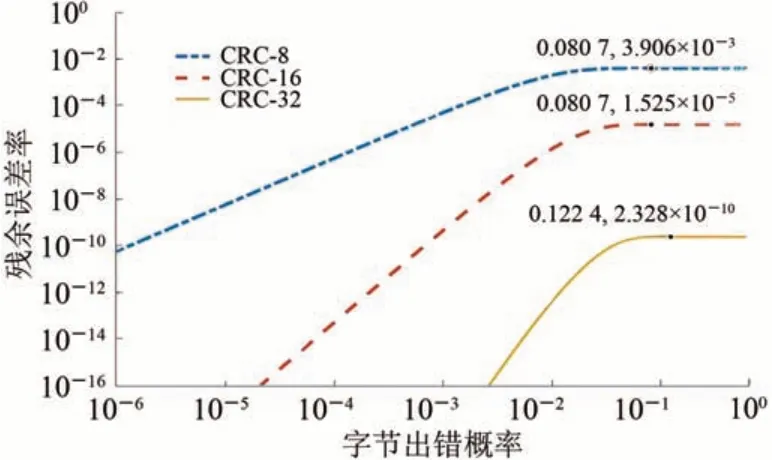
图2 待校验数据位长256 bit时3种CRC多项式残余误差概率

根据图2计算结果可知：CRC残余误差概率随字节出错概率的增加而增长，8 位特征多项式计算结果最终稳定在3.906×10-3，数量级符合2-8；16位最终稳定在1.525×10-5，数量级符合2-16；32位最终稳定在2.328×10-10，数量级符合2-32。

CRC 多项式校验时，其待校验数据位长一般都小于2r-1-1位［16］。例如：8位CRC多项式，待校验数据位长一般不超过28-1-1=127 bit；16位一般不超过32 767 bit。因此，对于数据位长256 bit 的无线传感模块，若选用8 位CRC 校验码，待校验位超过127 bit，漏检率高，无法保障接触网监测模块数据传输可靠性；若选用24位或32位CRC 校验码，则校验效率低，且校验位占用较多空间，数据传输有效率降低、运算周期长、资源占用大。综合对比后，可认为16 位CRC 校验码更适用于256 bit的数据位长校验。

1.3 影响残余误差概率的因素

CRC 校验码实际是1 种缩短汉明码［17］，实际计算过程中，其位出错概率ε随合法码字中码重为p的码字数目的增加而增加。为简化残余故障概率计算过程，通常采用含最小汉明距离的近似模型进行计算［18］，即

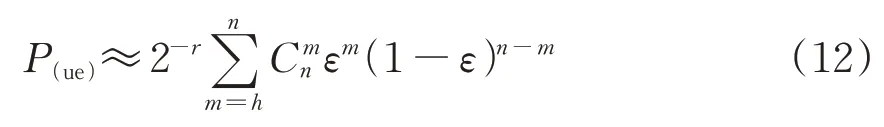
式中：h为最小汉明距离（HD），bit；m为出错位数，bit。

式（12）即是近似残余误差概率模型。CRC多项式校验数据位长固定的情况下，不同最小汉明距离对应多个不同CRC 多项式。仍取待校验数据位长256 bit（其他数据位长情况类似），按照16 位CRC 多项式校验，仿真计算不同最小汉明距离下的残余误差概率，发现最小汉明距离为4时，所有小于4 bit 的错误均可被检测出；同理最小汉明距离为6 时，所有小于6 bit 的错误也均可被检测出。因此选取最小汉明距离分别为4，5 和6 bit，采用MATLAB 进行仿真计算相对应的16 位CRC 多项式的残余误差概率，仿真结果如图3所示。

图3 待校验数据位长256 bit时不同最小汉明距离对应的16位CRC多项式残余误差概率

根据图3 仿真结果可知：待校验数据位长256 bit 且字节出错概率相同时，最小汉明距离越大残余误差概率越小，但最小汉明距离每增加1 bit，计算所需位空间也相应增加1 bit；随BSC 信道位出错概率增加，不同最小汉明距离下的残余误差概率最终都逐渐趋于2-16；若只考虑残余误差概率性能因素，位长固定时应优先选取最小汉明距离较大的特征多项式。

由式（12）可知，残余误差概率还与数据字节位数有关。取位出错概率为0.1，最小汉明距离为4 的16 位CRC 多项式，其字节位数与残余误差概率关系如图4所示。

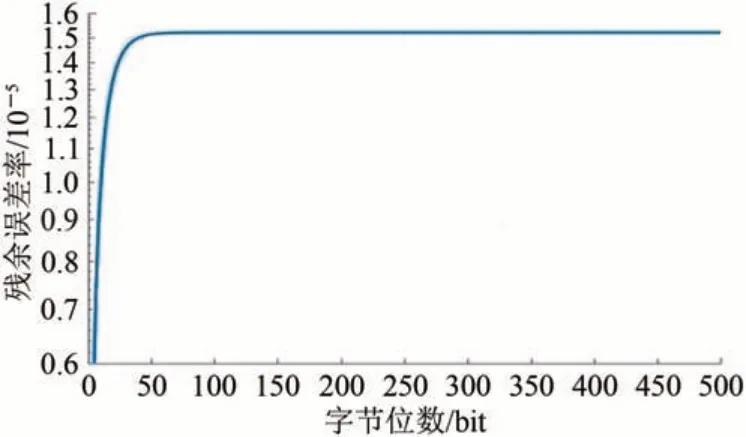
图4 最小汉明距离为4时16位CRC多项式字节数与残余误差概率关系

根据图4 可知：随待校验位长的增加，残余误差概率是1条无限逼近于定值的单调递增曲线；数据位长在50 bit 以内时，数据位数对残余误差概率影响很大；数据位长大于50 bit 后，这一影响越来越小，残余误差概率随位数的增加逐渐稳定于2-16；待校验数据位长达到256 bit 后，残余误差概率已趋于稳定。

图3 和图4 的结果均表明，最小汉明距离和数据位长均是影响残余误差概率的重要因素；数据位长的确定，则须结合最小汉明距离和实际设计需求选择合适的特征多项式；多项式残余误差概率与待校验数据位长、最小汉明距离、CRC 校验码位数和字节出错概率直接相关。

2 特征多项式检错性能定量评估

2.1 特征多项式的精确选取方法

考虑实际高速铁路沿线复杂的电磁环境、电磁干扰严重，信道环境不够稳定，此时位出错概率ε维持较高值，不同最小汉明距离对应的16 位特征多项式残余误差概率都趋于2-16。因此，对256 bit待校验数据位长进行校验时，选取最小汉明距离为4 的16 位CRC 多项式不仅可获得与最小汉明距离为6时相似的残余误差概率，同时还可节省更多的位空间。

提出1 种特征多项式的精确选取方法，其具体步骤如图5所示。首先根据应用场景，对部分适用特征多项式进行初步筛选；之后通过近似残余误差概率模型简单计算，快速选取性能更优特征多项式；然后，根据模型计算结果，若发现得到的特征多项式性能接近，则对特征多项式位漏检率进行精确定量计算，准确选取更优特征多项式。从计算原理可知，此方法计算简单，且适用于任意数据位长校验时性能更优特征多项式的选取。如进行CRC多项式校验时，可结合具体应用环境、待校验位长、信道位出错率、各特征多项式固定位长对应的最小汉明距离及具体漏检率等因素，运用此方法逐步判断各特征多项式的检错性能优劣，便可筛选得到性能更优的特征多项式。

图5 特征多项式选取具体方法

当待校验数据位长256 bit、最小汉明距离为4时，CRC-ANSI 多项式、CRC-CCITT 多项式为应用最广泛的2种16位通用特征多项式。其中：前者多用于Modbus和USB 等场景；后者多用于高级数据链路控制（HDLC）、FCS和蓝牙等场景。这2个特征多项式都包含x+1因式，在最小汉明距离、数据位长都相同的情况下，计算得到的残余误差概率接近，难以根据近似模型简化计算并直接比较特征多项式性能优劣。针对此类近似性能特征多项式的准确选取，有必要进一步根据实际校验数据位长分析各特征多项式位出错发生时所有可能的漏检情况，精确计算不同位长出错时的漏检率，定量分析特征多项式校验性能。

2.2 2种近似性能特征多项式检错能力对比

CRC-ANSI 多项式和CRC-CCITT 多项式的性能近似，均可检测出所有奇数位错；待校验数据位长256 bit 时的最小汉明距离均为4。根据Koop⁃man P［19］的研究结果，总数据位长272 bit（含16 bit 验位）时，CRC-ANSI 多项式和CRC-CCITT多项式的检错能力见表1。

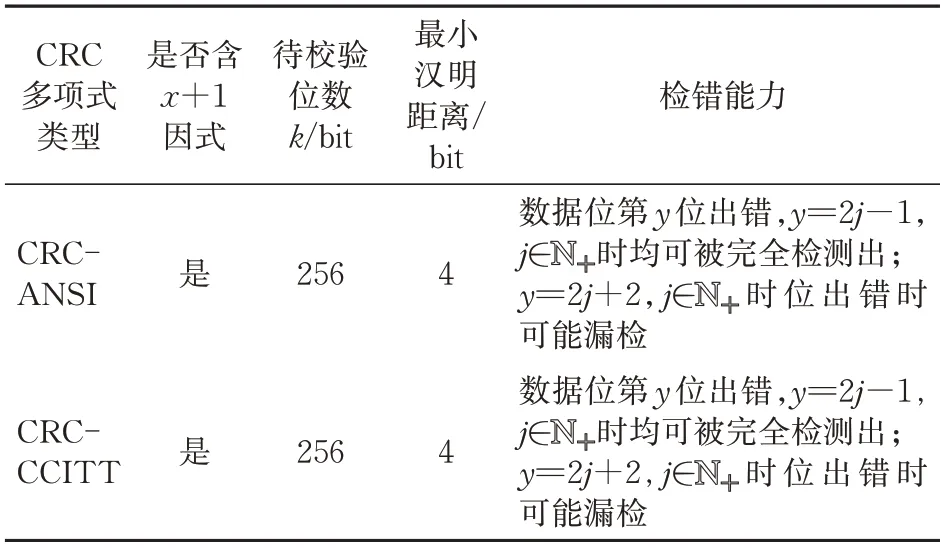
表1 总数据位长272 bit时2种多项式检错能力对比

根据表1，CRC-ANSI 多项式和CRC-CCITT多项式发生位出错时，可被完全检测和未被完全检测情形一致，因此需对位出错可被完全检测出的具体概率和未被完全检测出的具体概率即漏检率分别按位定量计算，具体分析特征多项式检错性能。

BSC 信道模型中，位出错漏检率与待校验数据位长、位出错率及所选特征多项式有关。当总数据位长为n的数据中出错位数为m时，共有种出错可能，出错概率为P(m，ε)=

根据表1，总数据位长272 bit 时，分可被完全检测和未被完全检测2 种情况，分别计算2 种特征多项式下位出错的检出情况。

1）可被完全检测时

求和得到2 种特征多项式下，出错位可被完全检测的概率P1为

2）未被完全检测时

根据Koopman P 的研究结果，0≤m≤3 或m=2j-1（3≤j≤136）时，am=0，bm=0；m≥4时，对CRC-ANSI 多项式有a4=19 233，a6=18 209 209，a8=20 614 494 970，对CRC-CCITT多项式有b4=6 587，b6=16 262 773，b8=20 437 276 732。

总数据位长272 bit 的信息中出错位数不少于3 bit 时，CRC-ANSI 多项式下偶数位出错的可被检测概率P2A和漏检概率Pue，ANSI分别按式（14）和式（15）计算。

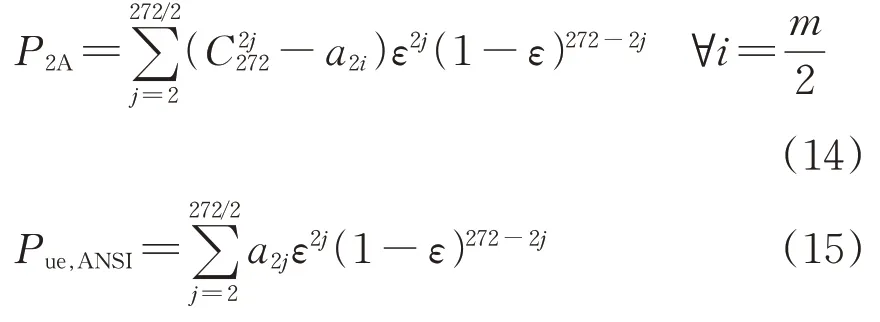
总数据位长272 bit 的信息中出错位数不少于3 bit 时，CRC-CCITT 多项式下偶数位出错的可被检测概率P2C和漏检概率Pue，CCITT分别按式（16）和式（17）计算。

综合位出错可被完全检测和未被完全检测2 种情形，得到总数据位长272 bit 时，CRC-ANSI 多项式下总检错概率PANSI=P1+P2A，即

CRC-CCITT 多项式下总检错概率PCCITT=P1+P2C，即

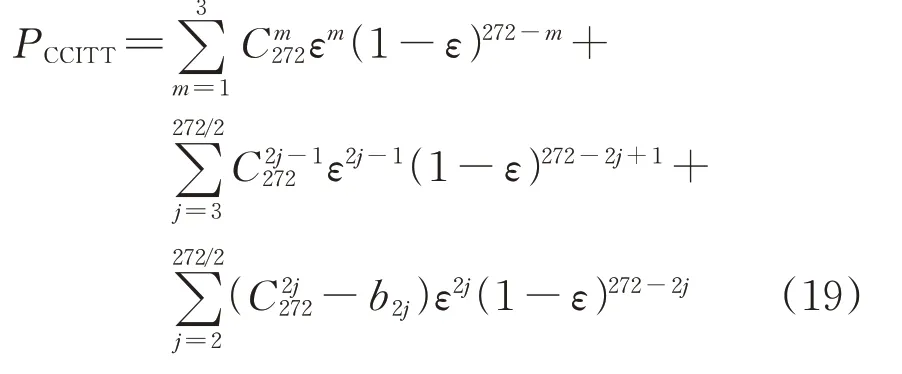
2.3 2种特征多项式漏检率对比

由式（18）和式（19）可知，特征多项式的漏检率与其对应的漏检数直接相关，CRC-ANSI 多项式与CRC-CCITT 多项式的检错能力则分别取决于其位出错漏检数am和bm。

将上述am值代入式（15），得到CRC-ANSI多项式的漏检率为

将上述bm值代入式（17），得到CRC-CCITT多项式的漏检率为

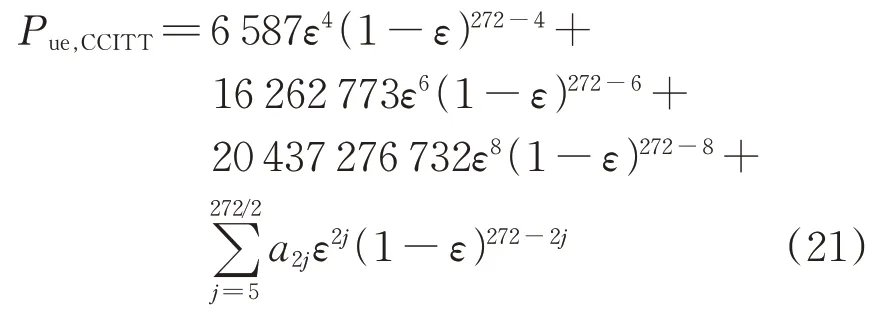
根据上述推算，Pue，ANSI和Pue，CCITT包含0～272 bit 出错所有可能的漏检情形。对数据位长272 bit时，CRC-ANSI多项式和CRC-CCITT多项式漏检率仿真计算的结果如仿真软件截图如图6所示。

图6 2种特征多项式漏检率对比

由图6 可知：2 种特征多项式下漏检率均随位出错概率的增加而增长；当位出错概率ε≤10-3，ε相同时CRC-CCITT 多项式的漏检率明显更低；当ε>10-3，ε相同时两者漏检率趋于相同。因此，在BSC信道模型中，当CRC-ANSI多项式和CRCCCITT多项式发生同种漏检情形时，CRC-CCITT多项式的整体漏检率明显更低。

若出错位数为m且m>9 bit时，对应的具体漏检数未给出，则am和bm值均为此时所有漏检都发生情形下的漏检数。仍设出错位数为m，假设此时CRC-CCITT 多项式中所有漏检情形同时发生，则Pue，CCITT为CRC-CCITT多项式最大漏检率，式（21）不变；假设此时CRC-ANSI 多项式中所有漏检情形都未发生，则Pue，ANSI为CRC-ANSI 多项式最小漏检率，可由此将式（20）变形为

对CRC-CCITT多项式最大可能漏检率和CRCANSI 多项式最小可能漏检率进行计算，计算结果根据Mathematic仿真软件截图如图7所示。

图7 CRC-CCITT多项式最大漏检率与CRC-ANSI多项式最小漏检率对比

由图7 可知：CRC-CCITT 多项式最大可能漏检率和CRC-ANSI 多项式最小可能漏检率在同一位出错概率的交点坐标（5.422×10-3,3.682×10-6），当位出错概率ε<5.422×10-3时，相同信道环境中CRC-CCITT 多项式最大漏检率都小于CRC-ANSI 多项式最小漏检率；信道位出错概率小于5.422×10-3且出错位数为m时，无论存在哪种未被检测可能，CRC-CCITT 多项式的漏检率都一定低于CRC-ANSI 多项式；校验数据位长272 bit（含16 bit 校验位）时，CRC-CCITT 多项式在出错位数较低时的具体漏检数及0～272 bit 出错漏检率都相对更低，说明CRC-CCITT 多项式的整体检错性能更优。

由此，设计接触网在线监测无线传感模块数据包时最终选取CRC-CCITT 多项式对272 bit 数据位长进行CRC多项式校验。

3 结论

（1）针对生成形式为g（x）=（x+1）p（x）的特征多项式，在推导残余误差概率序列计算方法的基础上，通过仿真计算发现，特征多项式残余误差概率与待校验数据位长、最小汉明距离、CRC校验码位数和字节出错概率直接相关；16 位CRC 多项式更适用于待校验数据位长为256 bit时的情况。

（2）提出1 种可定量评估CRC 多项式性能的简单计算方法，适用于任意数据位长校验时更优性能特征多项式的精确选取。应用CRC 多项式校验时，都可在结合具体应用环境、待校验位长、信道位出错率、各特征多项式固定位长对应的最小汉明距离及具体漏检率等因素的基础上，运用此方法逐步判断各特征多项式的检错性能优劣，筛选出性能更优特征多项式。

（3）当无法通过近似残余误差概率模型快速计算并直接比较2 种相近性能特征多项式的优劣时，可对存在位出错未被检测出的所有可能情形进行分析，便可准确计算其具体漏检率，并进一步筛选比较特征多项式之间的性能。在BSC 信道下，运用CRC-ANSI 多项式和CRC-CCITT 多项式精确定量计算总数据位长272 bit（含16 bit 校验位）时的位出错漏检率，发现位出错概率小于5.422×10-3时，CRC-CCITT 多项式的漏检率更低，整体检错性能更优。