基于隔振垫超弹性本构模型的橡胶浮置板轨道动力仿真

王启好，蔡小培，常文浩，侯博文，王 涛，张朝明

（北京交通大学 土木建筑工程学院，北京 100044）

城市轨道交通易引起沿线环境振动等问题［1］，线路建设前应进行动力学仿真预测，必要时需采取轨道减振措施。橡胶浮置板轨道广泛运用于我国城市轨道交通中，尤其在人口密集区地下线大量铺设。橡胶浮置板轨道中的橡胶隔振垫是一种高分子非线性材料，其力学行为准确表达与否将直接影响轨道动力学计算结果，线弹性本构无法准确模拟隔振垫的非线性力学行为，动力作用下材料非线性特征会进一步放大，进而影响橡胶浮置板轨道的减振效果预测。因此，有必要研究超弹性本构模型在橡胶浮置板轨道动力仿真预测中的应用，这对于减振轨道的设计选型和控制环境振动具有重要的意义。

橡胶浮置板轨道通过降低轨道刚度隔离耗散轮轨冲击振动，从而实现环境振动的控制。橡胶隔振垫是影响减振轨道刚度的关键结构，研究中存在隔振垫橡胶材料弹性难以准确模拟的问题，导致轨道变形与减振效果同时准确预测难度大。国内外学者对轨道用橡胶的动力特性进行了一系列研究。Maes［2］测试了铁路扣件胶垫的非线弹性动力行为，为扣件胶垫的非线弹性数值模拟提供了试验数据。Thompson 等［3］通过室内试验和现场试验，研究了扣件弹性垫层的高频动态性能。Kraskiewicz等［4］对有砟轨道道砟垫进行了室内试验研究。Cai等［5］通过现场试验研究了地铁直线段和曲线段弹性长枕轨道的振动控制效果。Zhao 等［6-7］通过长期现场试验，研究了橡胶弹性垫层在高速铁路高架桥的减振降噪效果。马蒙等［8］测试了列车荷载和定点锤击荷载作用下浮置板轨道的动力特性和减振效果。Wei 等［9-10］研究了扣件胶垫动刚度频变对地铁隧道环境振动的影响。王启好等［11］基于Mooney-Rivlin 超弹性本构模型，进行了弹性长枕轨道动力仿真，给出了枕下胶垫邵尔硬度建议值。综上可知，现有研究大多是对轨道用橡胶的室内试验和现场测试，对隔振垫应用效果的模拟预测较少。此外，现有橡胶浮置板轨道隔振垫的动力仿真研究中，隔振垫多采用线弹性本构，不能反映橡胶材料应力应变的非线性关系。

本文以城市轨道交通隧道内橡胶浮置板轨道为研究对象，建立车辆-轨道-隧道耦合动力分析模型，并考虑浮置板轨道橡胶隔振垫的超弹性本构模型，研究超弹性本构模型下橡胶浮置板轨道的动力响应和减振效果，并与线弹性模型进行对比。

1 橡胶隔振垫超弹性本构模型

超弹性本构模型是一种常用的非线性材料模型，在动荷载作用下材料的应力应变关系呈现非线性特征，以弹性能函数的形式一一对应。隔振垫为橡胶材料，具有超弹性。考虑铁路轨道系统中隔振垫变形小、受力方向单一等特点，采用Mooney-Rivlin 模型（M-R 模型）来表征橡胶材料的超弹性属性。M-R 模型基于连续介质力学理论，先假定应变能函数，再由应变能函数对主伸长比求偏导得到橡胶材料主应力［12］。各向同性不可压缩材料的M-R超弹性本构模型应变能函数W为

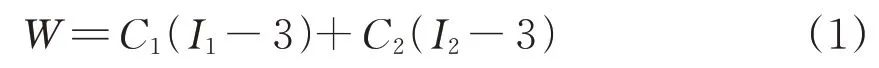
式中：C1和C2为材料超弹性力学性能常数；I1和I2为与主伸长率相关的变形张量不变量。

铁路轨道系统中隔振垫变形小，橡胶材料处于小应变状态，此时材料超弹性力学性能常数C1和C2与弹性模量E0、剪切模型G关系为

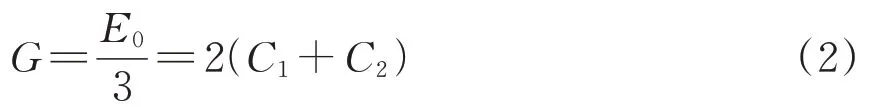
根据参考文献［12］，C1和C2存在比值关系，当C2/C1取0.05时，模拟的变形荷载关系最接近橡胶实测表现。确定C2与C1比值后，即可唯一确定超弹性本构模型参数取值。

隔振垫刚度一般采用静刚度Ksta表征。静刚度定义为在作用力均匀分布的条件下，连续弹性件的单位面积静刚度，可通过下式计算

式中：F1，F2为施加在隔振垫上的荷载，分布为1.8和9.0 kN；D1，D2分别为加载至对应荷载时隔振垫的位移，mm；S为隔振垫面积，m2。

城市轨道交通线路类型多样，沿线环境条件复杂，需根据具体工程减振需求因地制宜地进行特定减振设计。综合考虑建设经济性、线路运行安全及减振效果，橡胶浮置板轨道隔振垫刚度需进行不同设计。根据相关文献［4］及规范［13］得到实际工程中不同型号隔振垫的小应变弹性模量以及静刚度数据，进而计算得到不同型号隔振垫的超弹性参数C1和C2，见表1。浮置板底部隔振垫静刚度根据隔振垫型号选取，浮置板侧面隔振垫静刚度统一为0.1 N· mm-3，后文将直接采用静刚度值代表不同型号的隔振垫。

表1 不同型号隔振垫的材料参数

为验证M-R 超弹性本构模型的合理性，根据文献［4］建立仿真模型，采用1.2 的动静刚度比，分别计算5 和10 Hz 动荷载作用下的动刚度K5和K10并与试验数据进行对比，见表2。由表可知，5和10 Hz 动荷载作用下动刚度的仿真计算值均与试验值相近，表明该模型可真实反映橡胶隔振垫的动力行为。

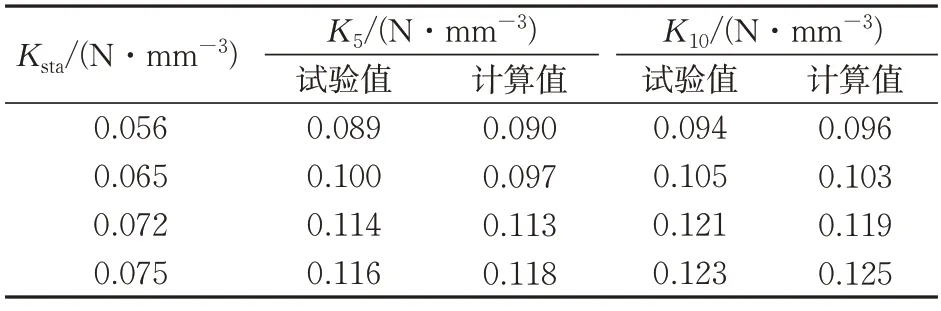
表2 动刚度计算结果与试验数据对比

2 地铁车辆-橡胶浮置板轨道-隧道耦合动力分析模型

地铁车辆简化为31 自由度多刚体系统模型，选取地铁B型车，车体几何参数和一二系刚度阻尼参照文献［1］选取，车体时速100 km。轮轨相互作用采用Hertz 非线性弹性接触模型和经典库伦摩擦模型计算［14］。根据北京地铁轨道谱［15］生成2～25 m波长范围不平顺，叠加随机短波不平顺，最终得到的轨道垂向不平顺和横向不平顺如图1所示。

图1 轨道不平顺

橡胶浮置板轨道结构自上而下分别为钢轨、扣件、轨道板、橡胶隔振垫和基底。根据北京某地铁工程选取轨道参数，建立200 m 长轨道模型。钢轨采用60 kg·m-1类型；扣件采用WJ-7A 型，垂向静刚度35 kN·mm-1，纵向间距625 mm；轨道板采用C60 混凝土，为现浇长板结构，长25 m、宽3 m、厚0.5 m；隔振橡胶垫采用全铺式，厚度30 mm，填满浮置板板底及两侧，根据不同的隔振垫刚度工况及本构关系设置弹性模量及超弹性参数；基底采用C40混凝土，视为U型槽结构，下部与隧道仰拱绑定约束。有限元模型中钢轨、轨道板、基底均采用C3D8R 实体减缩单元模拟，扣件系统采用弹簧-阻尼单元模拟。

地铁中轨道基底与隧道壁相连，隧道壁周围为土体。隧道壁管片为C35混凝土；忽略隧道壁与土体间相对位移，采用绑定约束；近场土体采用Mohr-Coulomb 弹塑性本构模拟，弹性模量取0.3 GPa，土体摩擦角取45°，土体黏聚力取1.2 GPa；远场土体设置无限元边界，采用CIN3D8无限单元以降低振动在边界的反射，减少单元数量，提高计算效率。

最终建立的地铁车辆-橡胶浮置板轨道-隧道耦合动力分析模型如图2所示。

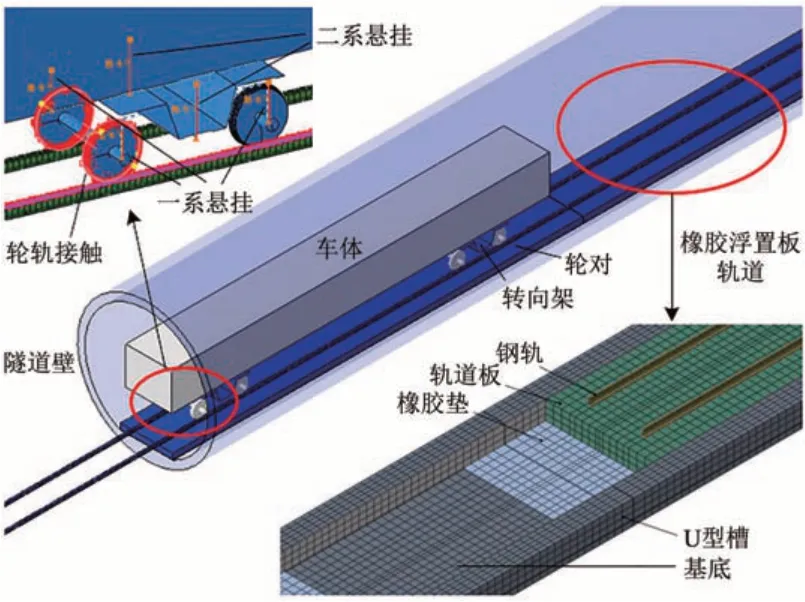
图2 动力分析模型

为验证模型可靠性，按参考文献［16］线路现场工况建立动力分析模型，分别采用超弹性本构和线弹性本构进行计算，并将计算结果与实测数据［16］进行对比，如表3和图3所示。

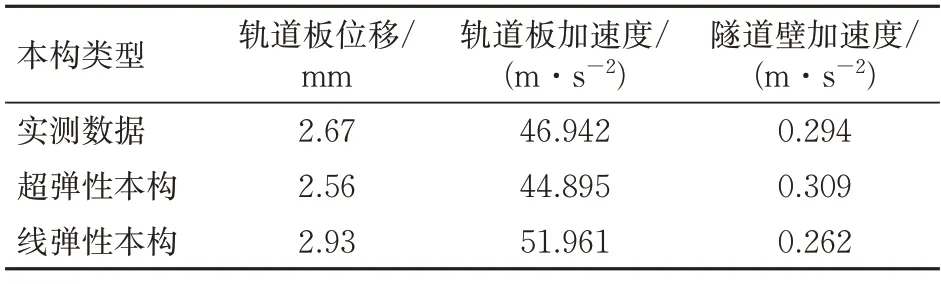
表3 轨道板与隧道壁动力响应

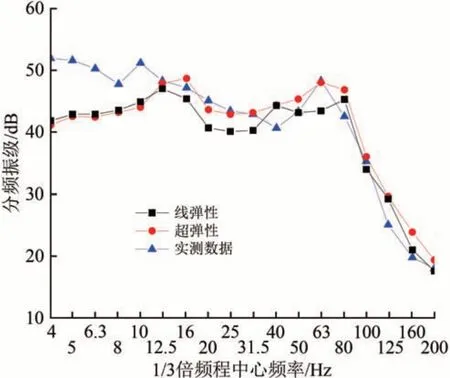
图3 隧道壁分频振级曲线

轨道动力响应是反映轨道结构动力性能，影响行车安全的重要指标，隧道壁动力响应是减振效果的主要评价指标。通常来说，仿真中轨道和隧道壁动力响应的模拟存在顾此失彼现象。轨道动力响应预测准确的情况下，隧道壁处减振效果一般偏差较大；隧道壁处减振效果接近实测的情况下，倾向于出现轨道动力响应预测失真。但由表3 可以看出，采用超弹性本构模型，在轨道板位移、加速度与实测数据更为接近的情况下，隧道壁加速度与实测数据的偏差相比线弹性模型也更小。由此可知，超弹性本构模型计算的各项动力响应指标均更接近实测数据，可同时实现减振轨道行车安全与减振效果的准确预测。进一步对比图3 中线弹性、超弹性本构模型仿真与实测隧道壁分频振级，发现线弹性本构模型计算的隧道壁分频振级整体偏小，在16～31.5 Hz 以及50～80 Hz 中心频率频段尤为突出，与实测结果差异大；超弹性本构模型计算的隧道壁分频振级更接近实测，仿真效果更好。综上，采用超弹性本构时，本文模型计算得到的轨道板位移和加速度、隧道壁加速度均与文献［16］实测结果相近，隧道壁分频振级在10 Hz 以上频段线形相近且主频一致，说明本文模型计算结果正确可信。

3 隔振垫超弹性本构模型对系统动力响应的影响

3.1 典型工况

选取隔振垫刚度0.019 N·mm-3为典型工况，计算并分析地铁列车动力荷载作用下采用隔振垫超弹性本构模型时轨道的动力响应。选取同一横截面处钢轨轨腰、钢轨正下方浮置板板中上表面和基底上表面位置提取垂向位移和加速度，进行时频分析，并与按参考文献［4］对应刚度参数取值采用线弹性模型计算的结果进行对比。

图4 为钢轨及轨道板位移时程曲线。由图4 可知：同一隔振垫刚度下，采用超弹性本构模型计算得到的轨道位移更小，钢轨、轨道板位移峰值相比线弹性本构模型分别降低了11.9%和33.9%。说明相较于线弹性材料，超弹性材料能为轨道提供更大的动刚度，轨道板更易保持稳定。

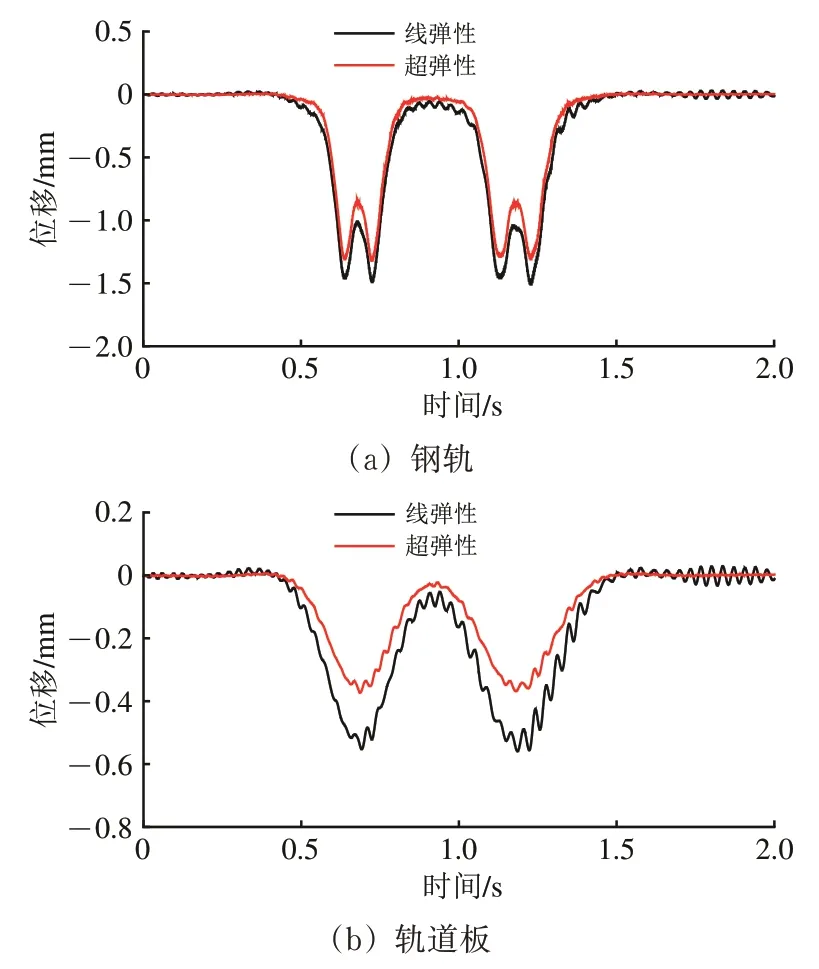
图4 钢轨及轨道板位移时程曲线

提取线路同一横断面处钢轨、轨道板和基底的加速度，对其进行低通滤波及傅里叶变换，得到加速度时频曲线如图5—图7 所示。其中，钢轨加速度滤波频率1 000 Hz，轨道板和基底加速度滤波频率400 Hz。

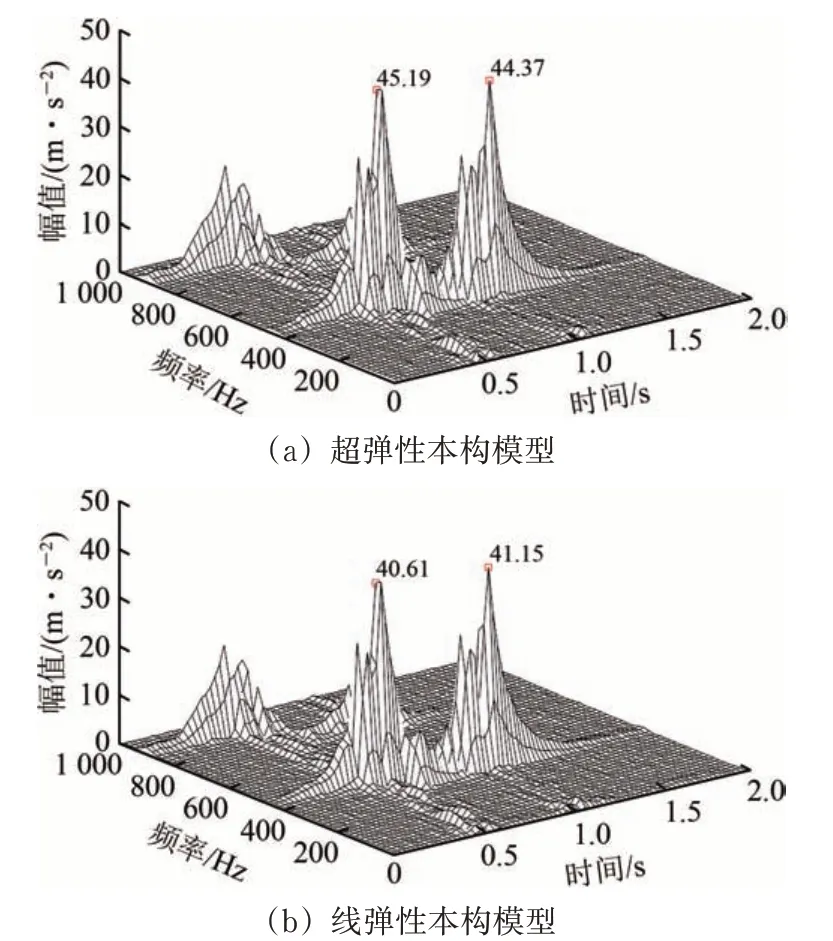
图5 钢轨加速度时频曲线

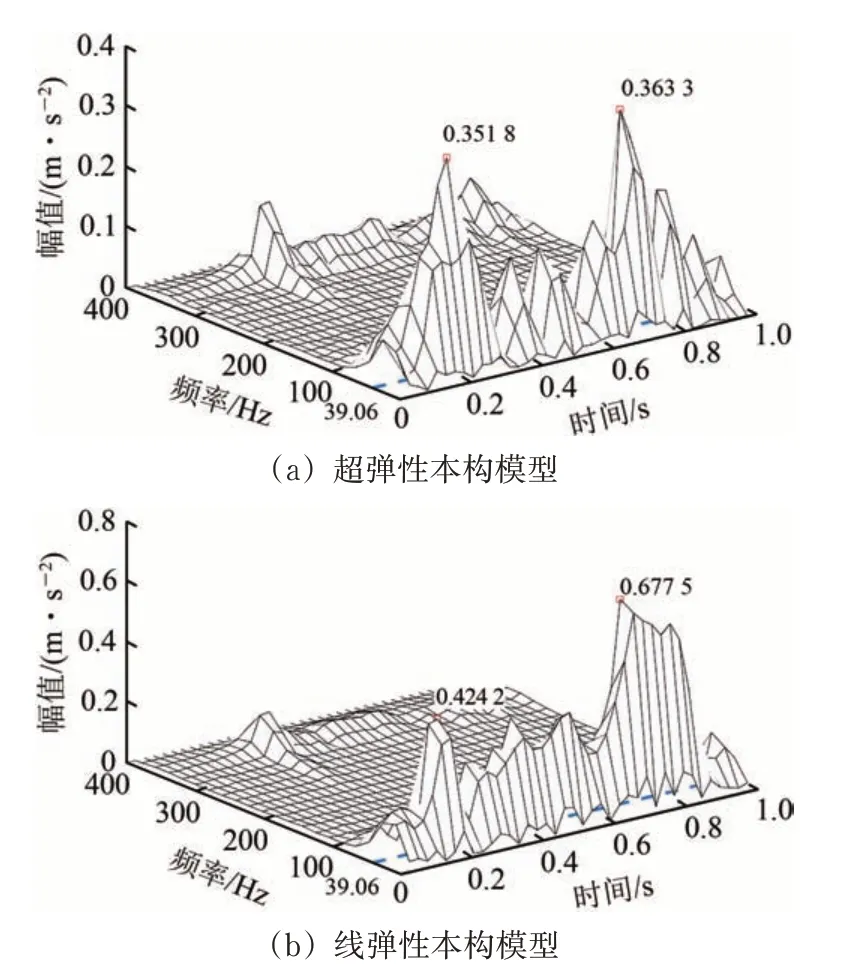
图6 轨道板加速度时频曲线

图7 基底加速度时频曲线

由图5—图7 可知：采用超弹性本构和线弹性本构计算得到的轨道结构各位置加速度时频峰值有所差异，但其对应的频率、时间均相近；2 种模型下钢轨加速度主频分别为371.1和449.2 Hz，峰值仅相差10.1%；轨道板和基底加速度主频均出现在39.06 Hz，线弹性模型计算得到的轨道板加速度较大，峰值相比超弹性本构模型大86.5%，超弹性本构模型计算得到的基底加速度稍大，峰值相比线弹性模型大22.6%。

结果表明，采用超弹性本构模型计算的轨道板加速度相对更小，基底加速度相对稍大。这说明超弹性材料能给轨道板提供更强支撑，有利于轨道板稳定，但同时也会引起基底较大的振动。根据橡胶浮置板的振动分布特性可知，隔振垫采用超弹性本构模拟时轨道板振动响应更大，能量耗散相对较低，导致基底振动能量更大，相应减振作用下降。

3.2 不同隔振垫刚度工况

轨道结构动力响应受隔振垫刚度影响显著［17］。根据工程实际选取不同刚度，每种刚度均分别采用超弹性本构和线弹性本构计算轨道动力响应，提取不同位置的最大位移和加速度，结果如图8 和图9所示。

图8 不同隔振垫刚度下的最大位移

图9 不同隔振垫刚度下的轨道各位置最大加速度

由图8 可知：与线弹性本构模型相比，采用超弹性本构模型计算得到的不同隔振垫刚度工况下钢轨和轨道板最大位移均较小，钢轨位移相差10%左右，轨道板位移相差40%左右，且轨道位移在低刚度区域变化更大、高刚度区域变化相对平缓；随着隔振垫刚度增加，2 种本构计算的钢轨和轨道板最大位移之差先增大后减小，在0.025 N ·mm-3处达到最大，在0.100 N·mm-3处最小，钢轨位移最小仅差4.2%，轨道板位移最小仅差27.3%。采用2 种本构模型得到的计算结果在低刚度工况下差异大、高刚度工况下差异小，说明采用超弹性材料可有效减小低刚度工况下的轨道结构最大位移。

由图9 可知：超弹性本构模型和线弹性本构模型对应的轨道不同位置加速度规律各不相同，超弹性本构模型计算的钢轨、基底加速度明显更大，线弹性模型得到的轨道板加速度较大；轨道板加速度随隔振垫刚度增大逐渐减小，基底加速度随隔振垫刚度增大逐渐增大，但超弹性本构模型轨道板加速度在0.025 N·mm-3出现突变，从4.111 m·s-2锐减到3.697 m· s-2，突变后轨道板加速度随刚度增加变化很小；当隔振垫刚度为0.025 N·mm-3时，2 种本构模型轨道板加速度差异最大，可达17.0%；当隔振垫刚度为0.100 N·mm-3，两本构模型基底加速度差异最大，可达145.6%。

随着隔振垫刚度增大，两种本构模型计算的轨道板振动差异减小，基底振动差异明显增大。对于基底振动而言，大刚度工况下超弹性本构模型的基底加速度峰值是线弹性本构模型的2.46 倍，线弹性本构模型基底振动预测准确性欠佳。隧道壁、土体振动均由基底传播而来，振动变化规律受基底影响，基底振动预测的准确与否将直接影响环境振动预测的可靠性。

4 隔振垫超弹性本构模型对系统振动加速度级的影响

由不同刚度下轨道动力响应分析可知，隔振垫超弹性本构模型的轨道动力响应与按参考文献［4］对应刚度参数取值计算的线弹性结果存在一定差异，基底位置尤其明显。环境振动由轨道基底、隧道壁传递而来，环境振动的大小直接受基底、隧道壁振动强度影响。橡胶浮置板轨道作为一种减振轨道，减振效果为其直接评价指标。为评价轨道减振效果，选取相同模型参数，计算了普通轨道条件下隧道壁的振动加速度。

将仿真计算得到的轨道板、基底和隧道壁（轨面以上1.25 m）加速度进行1/3 倍频程计权处理，得到各位置振动加速度分频振级，并计算减振轨道板到基底的传递损失［18］和隧道壁处减振轨道和普通轨道的插入损失［19］，选取人体相对敏感的1～200 Hz频段分析两种模型减振效果的差异。

4.1 典型工况

选取隔振垫刚度0.019 N·mm-3为典型工况。图10 为超弹性、线弹性本构模型计算得到的轨道板和基底的1/3倍频程分频振级。由图10可知：当频率为5～31.5 Hz 以及100～200 Hz 时，超弹性本构模型计算的轨道板分频振级明显小于线弹性结果，基底分频振级明显大于线弹性结果，最大分别相差7.46 和6.90 dB；当频率为40～63 Hz 时二者规律相反，最大分别相差2.24 和7.04 dB。相对于超弹性模型，线弹性本构模型会减小低频段基底振动，放大低频段轨道板振动以及高频段基底振动。

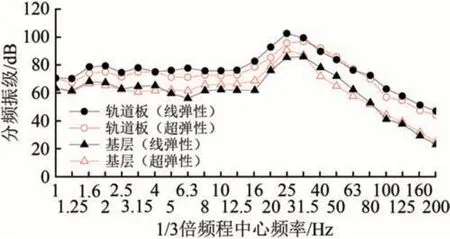
图10 轨道板和基底的1/3倍频程分频振级

图11 为超弹性、线弹性本构模型计算得到的橡胶浮置板轨道隧道壁1/3 倍频程分频振级，作为对比，图中同时给出了普通轨道计算结果。由图11可知：橡胶浮置板轨道在40 Hz 以上频段减振效果明显，普通轨道隧道壁分频振级在63 Hz 中心频段可达83.50 dB，而橡胶浮置板轨道此频段隧道壁振级在超弹性和线弹性本构模型下分别减小到35.22 和30.21 dB，二者相差5.01 dB；受轨道固有频率影响，橡胶浮置板轨道会放大隧道壁16～25 Hz 频段振动，20 Hz 中心频率处线弹性模型放大5.6 dB，超弹性本构模型放大8.53 dB，二者相差2.93 dB；线弹性本构模型计算得到的橡胶浮置板轨道减振效果大于超弹性本构模型；由于超弹性本构模型对橡胶隔振垫的实际动力响应的模拟更为准确，计算的减振效果更为保守，因此可为线路开通前环境振动评估提供更合理的参考。

图11 隧道壁的1/3倍频程分频振级

4.2 传递损失

图12为不同隔振垫刚度下超弹性、线弹性本构模型计算得到的传递损失。由图12可知：各工况下2 种本构模型计算的传递损失均随频率升高逐渐增大，隔振垫在高频区段作用效果好；除隔振垫刚度为0.019 N·mm-3工况个别频段外，线弹性模型的传递损失均大于超弹性本构模型，且高刚度工况下二者差异更明显，尤其是高频区段，传递损失差异最大可达7.13 dB。

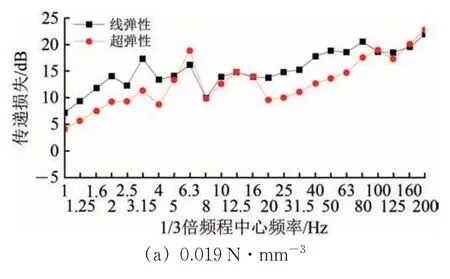
图12 不同隔振垫刚度下轨道分频传递损失

图13 为不同隔振垫刚度下根据1～200 Hz中心频率分频振级计算得到的轨道总传递损失。由图13 可知：当刚度由0.019 增大到0.100 N·mm-3，轨道总传递损失呈下降趋势，从30 dB 左右下降到20 dB 左右；线弹性模型总传递损失在各刚度工况均大于超弹性本构模型，2 种本构模型总传递损失差值先变大后减小。超弹性本构模型计算的传递损失较小，更为保守，环境振动评估中建议采用超弹性本构模型进行仿真预测。

图13 不同隔振垫刚度下轨道总传递损失

4.3 插入损失

图14 给出了不同隔振垫刚度下超弹性、线弹性本构模型计算的插入损失。由图14 可知：插入损失在25 Hz 中心频率附近为负值，与橡胶浮置板轨道在固有频率处振动放大有关；40 Hz 以上插入损失较大，且分频插入损失最大值对应频率随刚度增加向高频偏移，说明橡胶浮置板轨道在40 Hz 以上减振效果明显；与超弹性本构模型相比，采用线弹性本构模型会高估地铁振动特征频段（50～80 Hz）的减振作用，且放大了轨道固有频率（16～31.5 Hz）附近振动。

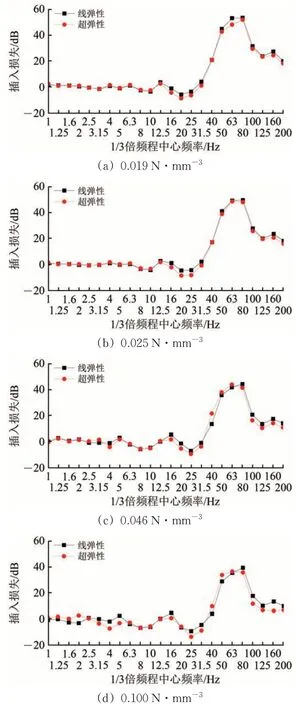
图14 不同隔振垫刚度下隧道壁振级分频插入损失

将1～200 Hz 中心频率分频振级按《城市区域环境振动标准》计算得到普通轨道和橡胶浮置板轨道对应的隧道壁总振级，将二者作差得到插入损失，普通轨道隧道壁总振级为83.49 dB。表4给出了超弹性和线弹性本构2 种模型计算的橡胶浮置板轨道隧道壁总振级及插入损失。

表4 橡胶浮置板轨道隧道壁总振级及插入损失

由表4 可知：减振效果与隔振垫刚度密切相关，随隔振垫刚度增大，隧道壁总振级逐渐增大，插入损失逐渐减小，不同刚度工况下插入损失最大可达9.30（线弹性）和11.53 dB（超弹性）；超弹性本构模型的插入损失比线弹性模型小，且随隔振垫刚度增大，二者差异逐渐增大，最大相差53.5%。线弹性模型减振效果偏大，尤其在高刚度工况下预测的环境振动偏小，建议采用超弹性本构模型进行减振效果预测评估。

5 结论

（1）相较线弹性本构模型，隔振垫超弹性本构模型计算的轨道结构及隧道壁动力响应均更接近实测数据，且传递损失更小、环境振动更大，即计算结果更保守，因此采用超弹性本构模型进行动力仿真及振动评估更为合理。

（2）不同隔振垫刚度工况下，隔振垫超弹性本构模型计算得到的轨道结构位移均小于线弹性本构模型，钢轨和轨道板位移峰值分别相差10%和40%左右，说明超弹性隔振垫能为轨道提供更大的动刚度，轨道板结构更易保持稳定。

（3）相较线弹性本构模型，隔振垫超弹性本构模型计算得到的轨道板加速度峰值较小而基底加速度峰值较大，且随隔振垫刚度增加，轨道板振动差异减小、基底振动差异显著增大，常用隔振垫静刚度范围（0.019～0.100 N·mm-3）内超弹性本构模型与线弹性本构模型计算的基底加速度峰值之比最大为2.46，采用线弹性本构将低估橡胶浮置板轨道的基底振动。

（4）相较线弹性本构模型，超弹性本构模型计算得到的轨道板振动及基底高频振动较小、基底低频振动较大，传递损失小，且2 种本构模型计算的传递损失差异随隔振垫刚度增大先增大后减小。采用线弹性本构模型将高估地铁振动特征频段（50～80 Hz）的减振作用，放大轨道固有频率附近（16～31.5 Hz）振动。