捕捉追问时机，提高课堂效率

江苏省无锡市宜兴范道中学 邵亦芬

追问是指针对某一内容追根究底地多次发问.有效的追问可启发学生的思维，帮助学生形成良好的问题意识，达到答疑解惑的目的[1].数学教学中的追问，一般有顺着学生思维与逆着学生思维两种情况.顺向追问一般是学生的回答不够深刻或比较片面，教师具有导向性的追问，让学生能深入思考，达到准确与深刻的地步；逆向追问则是在学生回答正确的基础上，反过来问学生答案的由来，以暴露学生的思维过程.

顺向追问更适合用于新知识点的教学，让学生在抽丝剥茧中逐渐认识到所学内容的本质与内涵；而逆向追问则适用于串联零散、碎片化的知识点，让学生在逆向问题的分析与解决中将零碎的知识编织成一张大网，让杂乱无章的内容变得更加系统化.鉴于此，笔者从自身的执教经验出发，浅谈数学课堂中的有效追问对学生数学思维的形成与发展的影响.

1 追问于思考不够深刻时

课堂中，常发现有一部分学生的思维会被教师或教材牵着走，从而出现沉默不语、懒得思考的现象.此时，有效追问，具有提神醒脑之功效.在学生思考积极性不高或对问题思考不够深刻的情况下，有效追问能立即刺激学生的神经细胞，让他们打起精神进行思考.同时，在问题的逐个解决中，学生体验到思考带来的愉悦感，从而对知识产生探究欲.

案例1“平行四边形”的教学

本章节的内容与其他几种图形(矩形、正方形、菱形等)的知识点具有异同点，不少学生学着学着就迷糊了，但又懒得去思考，总是处于一知半解的状态.为了激发学生的兴趣，让学生彻底搞清楚这些类似图形的性质，笔者特意设置了以下追问，以帮助学生更好地建构新知.

追问：(1)如何判定一个四边形是平行四边形？

(2)若在平行四边形基础上添加条件使之成为新图形，则你想增加什么条件？原图形变成怎样的新图形？

(3)若在菱形或矩形基础上增减一个条件，则你想增减什么条件？原图形会发生怎样的变化？

追问意图：这几种相似的四边形性质有着千丝万缕的联系，若逐个加以分析，学生虽然能说出来，但并不能明确这些图形之间具有怎样纵横交错的联系.三个追问的提出，不论回答哪个问题，首先，要清楚每种图形的性质，并在问题的思考与分析中对几种图形之间的关系产生了深刻的认识.此过程，在学生夯实基础的前提下，有效地激活了学生思维的灵活度，让学生对这几种图形的性质产生了更为深刻的理解，对本章节教学起到了显著的促进作用.

当学生思维处于疲软期时，有效追问可快速刺激学生的神经细胞，激发学生的思维意识，让学生进入深度思考状态，达到解决问题并建构新知的目的[2].因此，教师应时刻关注学生的课堂状态，选择在合适的时机给予合适、合理的问题刺激，这对提升课堂教学效率具有明显效果.

2 追问于学生思维的发散点

有效追问并非随意提出问题，而是在合适的时机有针对性地抛出一个接一个的问题.追问内容需与前一个问题有一定的相关性，常指向学生的思维发散点，让学生能从不同角度去观察与分析问题，在“横看成岭侧成峰”中达到知其然、知其所以然的目的.至于思维发散点的把握，需教师关注课堂与学生的状态.有价值的追问，方能凸显出问题的有效性.因此，何时、何处、如何问值得我们思考.

案例2“平方差公式”的教学

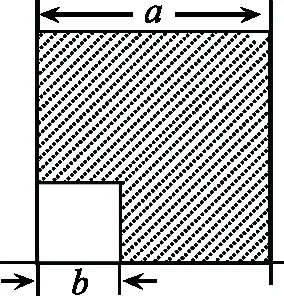
图1

如图1，小明从一张大正方形的纸张边上剪掉了一个小正方形，大、小正方形的边长分别为a，b.

问题(1)剩下图形的面积是多少？

(2)如图2，若将剩下的图形剪接成一个长方形，则长方形的长与宽分别为多少？面积又是多少？

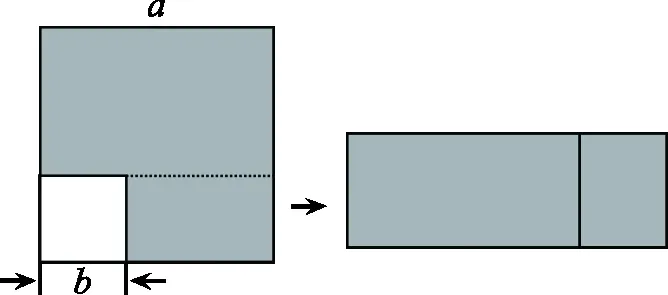
图2

(3)通过前面两问的分析与比较，是否能验证出平方差公式？

本问题难度较小，但只要亲手操作一下，即能很快找出问题的答案.因此，笔者让每个学生剪裁一张大正方形纸张，再截下一个小正方形.学生在操作、观察、比较与探索中拼出待求的长方形，问题在毫无悬念中很快得以解决.

为了让学生更加深刻地认识平方差公式，并学会从不同角度观察与思考问题，笔者提出追问：请大家寻找其他拼接方法来验证平方差公式.

学生在合作交流后，给出以下几种答案.

生1：如图3，可拼接成一个梯形，来证明平方差公式.

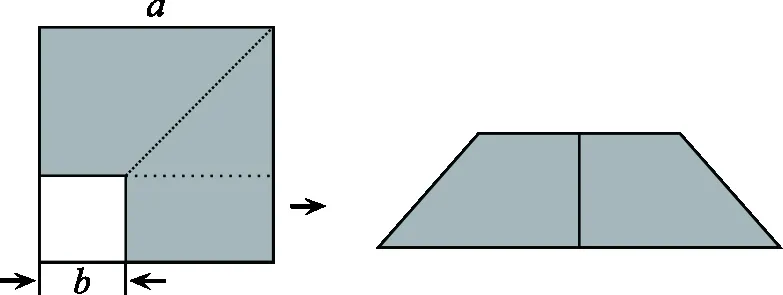
图3

生2：如图4，可将剩下的图形剪开，拼成一个平行四边形来验证.

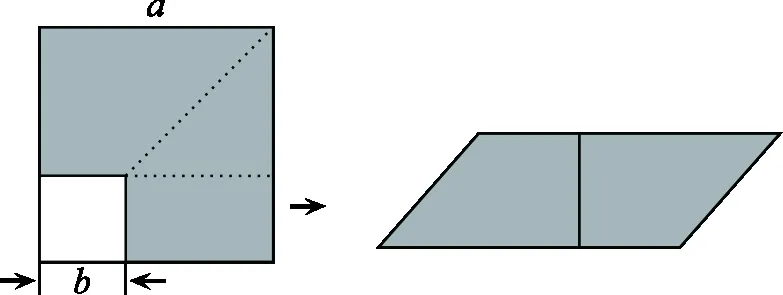
图4

生3：其实我们都被图2误导了，大家都想着用拼图来计算.事实上，可以将剩下的图形剪切为两个一样大小的直角梯形，通过梯形面积的计算即可得到平方差公式.

师：说说你的计算过程.

师：谈谈你们此刻的感受.

生4：没想到平方差公式可以用图形来验证，而且有多种方法，数学真是一门神奇的学科.

追问意图：这种方式摈弃了传统注入式的教学方法，而是引导学生先动手操作，边实践边思考，每个学生都能从自己习惯的角度去分析与观察问题，获得自主解决问题的办法；同时，受其他同学解题思路的影响，发现除了自身所看到的以外，还有更广阔的思维空间.这种有效追问的方式，激发了学生自主探究的能力，也有效拓展了学生的思维，让学生获得灵活面对各种问题的能力.

3 追问于教学问题的拓展点

教材所呈现的内容是针对大部分学生而设计的，教学时教师需从多个角度去发现与挖掘教材中更为深刻的内容，让学生形成思维的独创性.独创性是一种可贵的数学思维品质，对教学要求比较高.在问题的拓展点实施有效提问，能有效地激发学生产生独特、新颖的思维[3].

案例3“认识图形”的例题教学

如图5所示，△ABC是一块锐角三角形的钢板，AD为BC边上的高.已知BC=120cm，AD=80cm，若想将这块板加工成一个正方形，使新正方形的一条边在BC边上，两个顶点分别在△ABC的另外两条边上，求加工后正方形的边长.

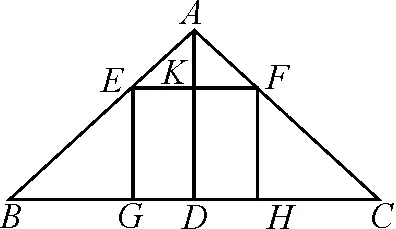
图5

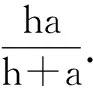
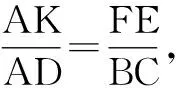
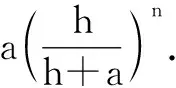
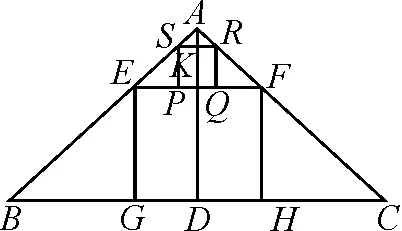
图6

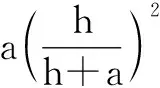
图7

追问3：如图7，在直角三角形ABC内有三个正方形，边长分别为a，b，c，求证：b=a+c.

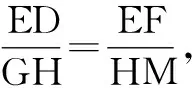
追问意图：逐层递进的追问，使学生更为深入地理解该部分知识，让思维具有独创性.追问1比较简单，处于学生的认知范围内，能很快激起学生探究的兴趣，因而解决此问没有障碍.随着追问难度的加深，学生的思维被彻底开发出来，学生在思维的驰骋中充分发挥各自的创造力，充分体现了思维的深刻性.

总之，问题是课堂教学的灵魂，在减负增效的背景下，高效性体现了教师的智慧与教育的艺术.利用有效追问能启发学生的思维掀起课堂的小浪花，演绎数学的精彩.因此，有效追问对培养学生的思维能力与数学核心素养具有深远的影响.