密集遮挡条件下的步态识别

高毅，何淼

（1.痕迹检验鉴定技术公安部重点实验室（中国刑事警察学院），辽宁 沈阳 110035；2.中国科学院 沈阳自动化研究所，辽宁 沈阳 110016）

1 引言

步态识别方法作为一种远距离非配合式身份验证方法，在安防、刑侦、社会保障等领域有重要应用。相比于人脸识别方案［1］，步态识别方法对于目标距离和分辨率的要求更低，也不需要拍摄清晰正面图像。相比于重识别方案［2］，步态识别方法对于目标服装配饰的改变鲁棒性更高，更适合于非配合式场景以及长时段目标搜索。对步态识别算法的研究在近几年来受到了越来越多的重视，成为新一代身份认证的关键技术［3］。

目前，主流的步态识别方法主要依赖目标轮廓序列作为输入，对目标身份进行识别，此外在近几年的研究中也有部分利用密集3D 表示作为输入的步态识别研究成果［4］，但是由于其对3D 姿态恢复［5］的依赖，落地应用相对较为困难。目前基于轮廓序列的步态识别算法主要分为三类：第一类方法将步态序列图像转化成单张步态能量图进行处理，后续的处理手段与人脸识别、行人重识别等方法类似。Chen［6］等人利用潜在条件随机场配合支持向量机对步态能量图进行处理，取得了较好的识别效果。Wu［7］等人在步态能量图的基础上利用卷积神经网络在不同场景下对多种预处理方法和网络结构进行了分析，得到的跨角度步态识别模型相比之前的方法精度有了较大提高。He［8］等人利用生成对抗网络学习不同视角下步态能量图的特征表示，对步态能量图进行了更一般化的表达。此类方法的网络结构较为简单，计算量更加可控，然而此类方法忽视了步态图像重要的时间信息，同时步态能量图的合成也使得部分空间细节信息变得模糊，使得方法对于相似目标的识别较为困难，普遍难以达到较高精度；第二类方法依靠时序卷积方法对步态轮廓连续序列图像进行处理，强调前后若干帧之间步态特征的连续变化，由于较高的短时识别效果得到了较好的发展。Liao［9］等人利用卷积神经网络提取目标的姿态关键点，并借助LSTM 分析其时序特征进行目标的识别。Wolf［10］等人将长步态序列切割成多个长度相等的短序列，并利用多视角的3D 卷积操作分析短序列内目标的步态轮廓信息。Wu［11］等人提出了针对步态识别问题的时空图注意网络，利用网络的一个分支对空间区域进行加权筛选，并构建了时空图描述时序的变化关系。然而此类方法最容易受到步频、采样频率等因素的干扰，在实际应用场景下性能会大幅降低；第三类方法以2019 年提出的Gaitset 方法［12］为代表，是一类不依赖步态图像顺序约束的步态识别算法，具有高度的灵活性，对于实际场景的应用具有明显优势。然而此类方法依然有其局限性。首先，和其他两类步态识别方法一样，Gaitset 方法的输入依赖于行人目标的轮廓提取，而无论使用实例分割方法还是使用运动目标检测方法，在行人密集遮挡较为严重的情况下所提取到的轮廓总会受到遮挡的影响，通过运动目标检测配合行人检测方法获取的轮廓会有冗余的响应，而通过实例分割方法获取到的目标轮廓会由于遮挡产生残缺，这种冗余和残缺会大幅降低步态识别方法的精度。第二，Gaitset 方法在对于背包、穿大衣等干扰场景的鲁棒性依然有待提高。最后，Gaitset 方法所提取的特征高达15 872维，对于实际使用中大范围长时段的步态匹配问题，如此高维的特征很难进行大规模快速匹配搜索。

针对上述问题，本文对Gaitset 方法进行了改进。一方面，在Gaitset 基础上添加基于随机二值膨胀的数据增广方法，在普通视角下模拟背包、穿大衣和密集遮挡场景的步态图像，提升算法对上述干扰的鲁棒性。另一方面，通过对HPP（Horizontal Pyramid Pooling）结构收益来源的分析，对HPP 结构进行退化，同时引入CoordConv方法增强特征的绝对位置辨识能力，既可以降低密集遮挡下其他目标的局部特征对于步态识别问题的干扰，又可以藉此简化Gaitset 方法后端结构，大幅减少模型的参数量和计算量。我们利用仿真得到的密集遮挡场景数据集、Casia-B 数据集以及Casia-C 数据集［13］对所提算法进行了测试。实验结果表明，所提改进对于Gaitset 方法均有明显效果提升。

2 密集遮挡条件下步态识别算法设计

2.1 密集遮挡场景步态轮廓仿真数据集

为对步态识别算法的抗密集遮挡鲁棒性进行定量分析，首先建立密集遮挡场景步态轮廓仿真数据集。本数据集依靠Casia-B 数据集的测试部分进行仿真生成，待测目标ID 为75～124，干扰目标ID 为1～124。

对于每张待测目标图像，随机选择来自随机其他ID 目标随机角度的随机轮廓图像作为干扰进行轮廓的合并。干扰图像的中心坐标范围为［0∶w，-h/2∶3h/2］，其中w和h为原始目标包络框的宽和高。生成数据如图1 所示。可以看到，得到的混合图像能够很好地模拟密集遮挡人群中目标轮廓的提取结果。当遮挡目标中心纵坐标处于［-h/2∶h/2］时，轮廓形态与目标身后存在其他行人干扰下监控视角的目标提取结果相似。当遮挡目标中心纵坐标处于［h/2∶3h/2］时，轮廓形态与目标被前方其他行人遮挡状态下监控视角的目标提取结果相似。最后，通过原始包络框位置重新将受干扰后的目标轮廓提取出来，得到待测图像。最终生成的数据集格式与Casia-B 数据集相同。

图1 密集遮挡场景步态轮廓仿真数据集Fig.1 Simulation dataset of gait contour in dense occlusion scene

2.2 基于随机二值膨胀的数据增广方法

数据增广方法在行人重识别领域大放异彩，REA 方法［14］在行人重识别领域对算法鲁棒性的提升具有明显效果。然而步态识别领域与行人重识别领域在图像特征中有着明显的不同。首先，步态识别方法的输入通常并非RGB 三通道的彩色图像，而是二值化的黑白目标轮廓掩膜。其次，步态识别领域遮挡干扰通常来源于能够运动的其他行人的轮廓，而非大量的固定遮挡物，形态普遍较为圆润。上述两个问题使得REA方法在步态识别领域不再有与行人重识别领域同等的明显效果。

为了提升算法对于部分遮挡、服装变化、配饰干扰等问题的鲁棒性，在步态识别领域提出基于随机二值膨胀的数据增广方法。首先随机选取图像的部分区域，将其提取出来，复制映射到与图像相同大小的全零矩阵中。得到待膨胀区域图像。进而利用随机大小和形状的膨胀核对待膨胀区域图像进行二值膨胀操作。膨胀核形状包括椭圆形和矩形。形状包括（3，3），（5，5），（7，7），（9，9），（3，7），（7，3）。膨胀后的图像和原图进行逻辑或运算操作，得到最终输出的增广图像。增广结果如图2 所示。可以看出，通过随机二值膨胀后的目标增广轮廓与目标受遮挡、服装变化以及配饰干扰情况下的干扰轮廓有一定的相似性。

图2 基于随机二值膨胀的数据增广效果Fig.2 Output of the data augmentation method based on random binary expansion

2.3 多尺度水平金字塔和CoordConv

在原始的GaitSet 算法中，后半部分的多尺度水平金字塔的参数量占了较大比重，降低了算法的鲁棒性。与此同时，多尺度水平金字塔输出的特征向量长达15 872 维，降低了后续匹配识别的速度，限制了算法的应用规模。

针对这一问题，首先对多尺度水平金字塔的精度收益进行分析。网络中存在两部分多尺水平度金字塔结构，一部分来自序列池化通道，即网络的主通道，另一部分来自多级全局通道，即网络的辅通道。与此同时，两个通道各自存在5个不同的尺度，即1，1/2，1/4，1/8，1/16，计算量和输出特征维度所占比例为1∶2∶4∶8∶16，依次递增。为验证HPP 结构不同尺度特征对于精度的贡献，对GaitSet 模型进行了裁剪测试，对比了0～180°之间11 个不同角度下的步态识别精度。本文中所有数据均为跨视角场景下的精度结果，即Probe 准确率是排除相同Gallery 视角的平均值。具体结果如表1 所示。

可以看出，HPP 结构中随着特征尺度的不断丰富，普通场景下获取的精度收益在不断降低，而干扰场景下的精度依然有大幅提升，此外计算量和参数量的增加速度却在不断提高。在这种情况下对HPP 结构进行优化和裁剪就变得极为重要。

直观地，通过裁剪小尺度特征图可以快速降低HPP 模块的参数量和输出特征向量的长度。然而表1 中的实验表明通过这种直观而简单粗暴的剪裁，得到的简化网络的特征精度同样会有大幅衰退。这种衰退主要有两方面原因：一方面，水平特征金字塔可以从侧面为特征提供一定的绝对位置信息，这种信息对于不同位置特征的区分以及前景遮挡和后景干扰具有重要意义。不同于处理自然图像时网络可以通过较大的感受野感受卷积补零的区域来获取大致的绝对位置信息，步态轮廓图像具有二值特性，网络无法分辨补零区域和原始背景区域，这种绝对位置信息也就无法通过卷积网络直接获取；另一方面，缩短特征向量的长度也会同时降低特征的部分表达能力。虽然过长的特征向量中存在大量冗余信息，但是不进行信息的冗余部分分析和筛选直接进行裁剪依然会裁掉大量关键的特征表达，降低最终的输出精度。

HPP 结构最早来源于行人重识别任务，其主要价值在于应对行人部件水平位置不对齐的问题，利用更少水平切割数的大金字塔尺度特征生成空间上相对松弛的距离表达。然而这种表达对于步态应用并不完全适用。重识别问题主要研究目标在不同相机拍摄场景下的匹配问题，通常由于摄像机的拍摄角度、拍摄距离以及拍摄时间的不同，目标在图像中的形态变化严重，很难严格对齐，但是摄像机提供的图像内目标纹理特征较为丰富，可以较好支撑非对齐状态下的特征提取和匹配，因此为了图像处理系统的简洁性，通常不在样本输入之前进行严格对齐，研究主要集中于对图像特征提取能力和鲁棒性的提升，需要算法对于图像间目标部件的不对齐问题进行适应。区别于重识别问题中图像丰富的纹理特征信息，步态序列中的单张图像内只有目标轮廓，信息远少于行人重识别任务，因此更加强调时序图像上手臂、腿部等重要部件的空间位姿对比，空间位置信息的时序变化对其十分关键，因此松弛的空间表达对于步态特征的学习是不利的。与此同时，由于每个样本都是序列图像而非单张图像，其内部本就存在对齐问题，通常在输入网络之前就需要将对齐问题提前解决，否则对于网络性能的影响是灾难性的，这一点在基于步态能量图的方法中体现尤其明显。而在空间严格对齐的情况下，HPP 结构并不会提升特征表达的信息量。如图3 所示，每个低分辨率的金字塔特征都能用更高分辨率的特征进行简单的平均或极值运算得到。最后，不同于标准SPP 空间金字塔，HPP 用在网络的最后端，对于多尺度特征的提取也并无明显作用。

表1 不同尺度的水平金字塔池化精度收益分析Tab.1 Analysis of accuracy benefit of horizontal pyramid pooling with different scales

图3 空间严格对齐的情况下HPP 结构的特征表达冗余问题Fig.3 Feature representation redundancy of HPP structure in case of strict spatial alignment

除了上述任务不适应问题之外，正如引言中提到的，HPP 结构引入了大量的参数量，并显著提升了目标特征表达的长度，一方面提升了算法在大规模检索时的计算代价，另一方面也给信息量本就比较少的步态特征提取问题带来了更多的过拟合风险。

因此本文并未对HPP 结构进行裁剪，而是直接对HPP 结构进行了改进，提出了退化水平金字塔结构，即DHPP（Degenerated Horizontal Pyramid Pooling）。如图4 所示，首先退化HPP 结构，仅保留116 的特征尺度，此时HPP 结构退化为PCB 结构。在此基础上，对平均池化和最大池化两个分支分别加入注意力结构对每个子区域选取的特征进行自适应加权和筛选。最终两个通道的输出特征按位相加得到最终的输出特征。与上述分析一致，在步态轮廓识别任务中我们发现退化后网络的参数量有了大幅降低，性能却反而有了小幅度提升。在针对遮挡问题的测试中，我们发现DHPP 去除了HPP 对于特征的空间位置表达相对松弛的问题，性能提升幅度更加明显。

图4 DHPP 结构示意Fig.4 DHPP structure

与此同时为进一步解决绝对位置信息难以获取的问题，在网络中引入了CoordConv 方法［15］。CoordConv 方法可以在网络中提供绝对位置信息作为特征补充，弥补卷积结构由于平移不变性造成的绝对位置信息缺失问题。这种问题在二值图像处理中表现得尤其严重。通过这种方法，可以一定程度降低剪裁多尺度水平金字塔对精度的影响。

2.4 网络训练方式和整体结构

在上述分析的基础上，对加入DHPP 结构的GaitSet 网络继续进行分析，判断退化后的小尺度水平分割特征在主通道和辅通道（即MGP）上的性能区别以及对于最终精度的影响。为了直观对比两个通道之间的区别，再此没有使用所提的数据增广方法以及引入的CoordConv 方法。分别利用原始数据集和密集遮挡数据集进行分析，判断两路通道对于不同场景下的适应性。具体结果如表2 所示。

表2 主/辅通道在不同场景下的识别精度Tab.2 Gait recognition accuracy of main and auxiliary channels in different scenarios

可以看出，网络辅通道的普通模式和背包模式特征表达能力通常略高于主通道，而主通道对于穿大衣这一严重干扰场景的鲁棒性明显更强。针对本文的主要应用，在密集遮挡场景下，主通道的整体价值要高于辅通道，对辅通道进行裁剪可以进一步降低网络的计算量以及参数量，并大幅降低特征向量的输出长度。

然而，如果在训练阶段就进行裁剪，仅通过主通道进行训练，变相减少了代价与特征之间的跳跃连接结构，减弱了信息的传播通路，降低了训练过程中的特征监督，会使得网络训练变得困难。如表3 所示，在训练阶段减除辅通道对于主通道的特征学习具有明显影响，而减除主通道代价分支之后辅通道的特征学习效果同样明显降低。

针对信息的传播通路的问题，我们使用训练联合-测试剪裁方法。训练过程中保留主通道的代价梯度信息方向传播，测试过程中将主通道完全剪裁，以降低算法的计算复杂度。网络整体结构如图5 所示。网络使用三元损失函数进行训练，其中margin 设置为0.2，具体如公式（1）所示。每批样本选择8 个ID 的16 个随机角度的步态轮廓图像集进行训练。每个图像集随机提取30 张乱序图像，图像分辨率为64×64。学习率设置为0.000 1。

表3 多通道训练与单通道训练的性能差异Tab.3 Performance difference between multi-channel training and single channel training

3 实验与分析

3.1 数据集与评价指标

为了定量评价算法的步态识别精度，本课题使用Casia-B 数据集中的ID 为1～74 的步态轮廓进行训练，并使用2.1 中生成的密集遮挡场景步态轮廓仿真数据集、Casia-B 数据集中ID 为75～124 的步态轮廓进行测试。此外为了进一步验证所提方法对目标不同行走速度的适应性，我们在Casia-C 数据集中也进行了训练、测试和对比。

图5 网络整体结构图Fig.5 Overall network structure

Casia-B 数据集是目前应用最广泛的步态识别数据集之一。数据集内同标注了124 个不同行人目标在正常、背包、穿大衣3 种形态下的步态序列图像。其中每个行人目标标注了正常状态下拍摄六组图像序列，背包状态下两组图像序列，穿大衣状态下两组图像序列。每组图像序列中均提取了0～180°中共计11 个角度图像的步态轮廓。该数据集并没有明确数据中的训练集和测试集范围，因此我们选择了目前最通用的方法进行数据的分割。训练集包括前74 个行人目标的全部数据，而测试集使用后50 人的图像。在测试集中使用普通条件的前4 个图像（NM-01-NM-04）作为目标参考图库序列，使用包括普通条件下后两个序列（NM-05，NM-06）、背包条件下的两个序列（BG-01，BG-02）以及穿大衣条件下的两个序列（CL-01，CL-02）作为待识别序列。Casia-B 数据集主要强调跨视角场景下步态识别方法的适应能力，同时也考验在目标衣着和配饰等表征发生变化时步态识别算法的鲁棒性。

密集遮挡仿真数据集通过Casia-B 数据集进行建立。在保持Casia-B 数据集原有视角变化和着装干扰的同时进一步提升了干扰的强度，目标除了衣着和配饰的变化之外，还会受到其他目标的遮挡，更有利于分析算法在密集遮挡场景下的鲁棒性。

Casia-C 数据集是一个在夜间场景下利用红外相机拍摄的大规模步态数据集。数据集中共包含153 人，每个人在包括正常行走、快速行走、慢速行走、背包行走4 种条件下进行步态采集。在本文的实验中将前33 人的步态数据作为训练集，后120 人的数据作为测试集。在测试集中使用普通条件的前2 个图像（fn00，fn01）作为目标参考图库序列，使用包括普通条件下后2 个序列（fn02，fn03）、背包条件下的2 个序列（fb00，fb01）、快走条件下的2 个序列（fq00，fq01）以及慢走条件下的2 个序列（fs00，fs01）作为待识别序列。Casia-C 数据集多用于测试步态识别算法对目标不同行走速度下行走姿态变化的鲁棒性，同时也可以进一步测试步态识别算法的全天时适应能力。

3.2 密集遮挡场景步态轮廓仿真数据集测试结果

本方法主要针对密集遮挡场景下的步态识别方法进行设计，首先使用自建的密集遮挡场景步态轮廓仿真数据集对算法性能进行测试，以GaitSet 方法作为基线算法，与改进算法进行比较。具体结果如表4 所示。

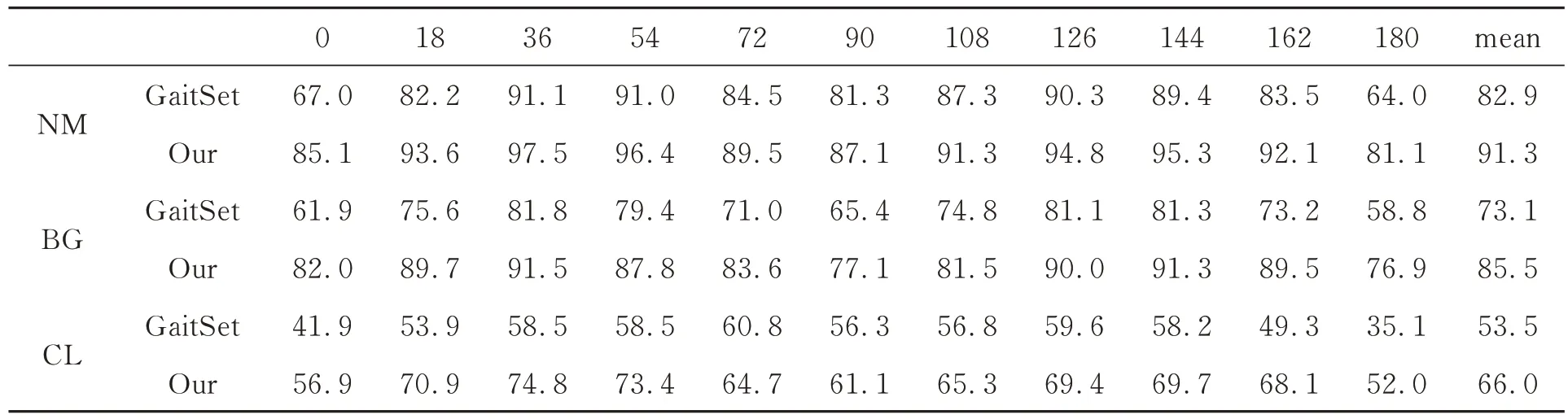
表4 在密集遮挡仿真数据集下所提算法与基线算法的性能对比Tab.4 Performance comparison between the proposed algorithm and the baseline algorithm in dense occlusion simulation dataset

可以看出，通过上述改进，改进后的方法对抗密集遮挡轮廓的鲁棒性相比于基线算法有了明显提高。通过精简，算法的输出特征维度有了明显降低，而在密集遮挡场景下鲁棒性仍然高于原始算法。

与此同时，可以看出服装和配饰对目标的局部遮挡能力越强，对步态识别方法的挑战就越大。背包场景下目标的两臂轮廓提取受到了一定的限制，而腿部轮廓变化并不受影响，对步态识别算法的精度影响相对较小。而穿大衣场景下目标膝盖以上部分的轮廓变化受到了大幅限制，算法仅通过小腿以下区域和两臂的轮廓特征变化对目标身份进行判断难度较大。本文所提方法在这两种干扰下性能所受的影响相比于基线算法都有所降低。

3.3 Casia-B 数据集测试结果

为了进一步验证算法的性能，在Casia-B 数据集上对比了更多近几年发表的相关算法，包括基于步态能量图的经典方法CNN-3D，CNNLB［7］，基于时序轮廓的经典方法STGAN［11］，近两年提出的最新方法Bi-Route［16］，ICNet［17］，Two-Path［18］，MBRDNet［19］以及我们的基线工作Gait-Set。具体结果如表5 所示。

很明显，本方法在非密集遮挡的理想条件下同样能够达到较高的步态识别精度，各项改进的加入并没有影响到算法在理想条件的效果。与此同时，方法对于服饰变化（穿大衣）以及配饰改变（背包）的鲁棒性有一定提高。所提算法相比于近几年提出的其他步态识别算法，整体精度有了一定提升。

基于步态能量图的方法精度相比于其他方法普遍较为落后，主要原因在于时序信息的丢失降低了方法能够提取的特征维度。大部分算法分别在36°和144°这2 个角度达到性能峰值，而在0°，90°和180°这3 个角度性能最差。这与不同视角下时序步态轮廓展示出的3D 姿态信息有着密切的关系。在侧面、正面和背面这三种情况下，步态轮廓信息表达出的关键部件空间变化维度会发生明显的降低，因此步态识别精度会大幅衰退。同时，和背面相比，正面轮廓能够较好表现出行人前脚轮廓的运动过程，步态特征辨识度相对更高。

3.4 Casia-C 数据集测试结果

接下来为了更加全面地测试所提算法的性能水平，同时验证所提方法对于行人在不同行走速度下姿态变化的鲁棒性，在Casia-C 数据集上进行了算法的性能测试和对比，对比方法包括FBC［20］，OFCD+PcA+LDA［21］以及我们的基线工作GaitSet。具体结果如表6 所示。

从实验结果中可以看出，所提方法对于目标行走速度不同带来的姿态变化鲁棒性较高。与此同时，在夜间背包场景下也可以看出所提方法相比于基线方法在局部遮挡鲁棒性上的优势。

表5 所提算法与其他最新算法在Casia-B 数据集上的性能对比Tab.5 Performance comparison of the proposed algorithm and other latest algorithms on Casia-B dataset

表6 所提算法与其他算法在Casia-C 数据集上的性能对比Tab.6 Performance comparison of the proposed algorithm and other algorithms on Casia-C dataset

3.5 消融实验

最后，为了验证提出的各项改进取得的效果，我们在两个数据集上对算法分别进行消融实验。首先在密集遮挡场景步态轮廓仿真数据集上进行测试，具体结果如表7 所示。其中C，R，D，T 分别对应引入CoordConv、随机膨胀、DHPP和联合训练裁剪，Dims 为输出特征向量长度。

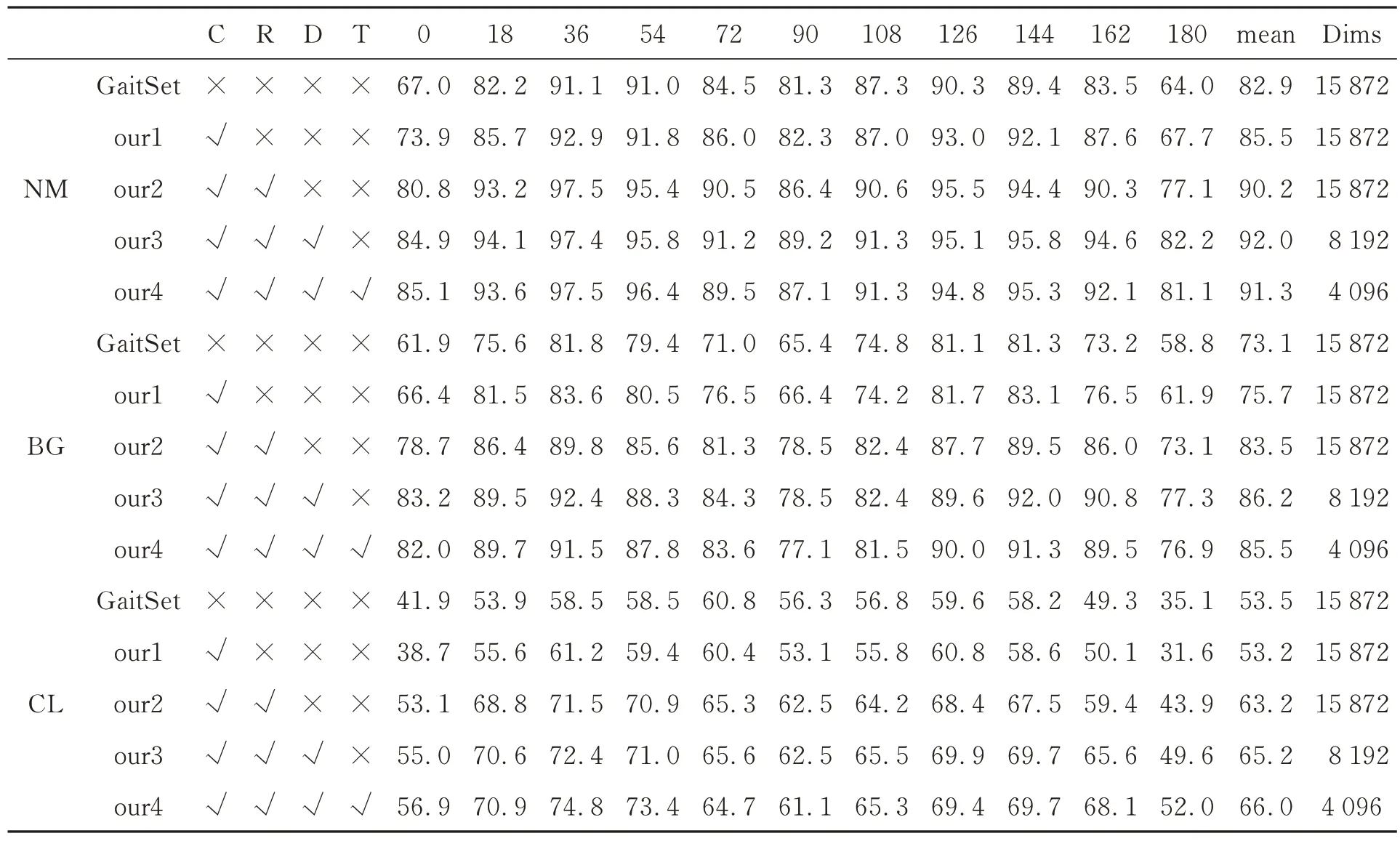
表7 在密集遮挡仿真数据集下所提算法的消融实验结果Tab.7 Ablation experimental results of the proposed algorithm on dense occlusion simulation dataset

可以看出，通过加入绝对位置信息，提升了步态局部特征的前后景区分能力，令特征提取更加集中于目标行人轮廓，算法在普通场景和背包场景的性能有了明显提升。通过加入基于随机二值膨胀的数据增广方法，提升了算法整体的抗过拟合能力，对于密集遮挡干扰鲁棒性和迁移能力有明显增强，从精度上看算法在密集遮挡数据集中三种场景下的精度均有大幅提升。与此同时，以上两项改进之间并不存在冲突，可以同时提升算法的识别精度和鲁棒性。最后，为了降低算法输出特征的维度，提高算法的实用性，对HPP 部分进行了改进，通过更加严格的特征空间表达和自适应的特征区域选取，算法整体精度进一步得到了提升，此外进一步配合联合训练方法对网络结构和输出特征进行裁剪，最终网络利用约四分之一的特征表达长度达到了远高于原始算法的精度水平。

进一步，我们在Casia-B 数据集上同样进行了消融实验。具体结果如表8 所示。

可以看出，通过加入CoordConv 提升绝对位置的感知能力，算法在背包场景下对干扰的鲁棒性有了明显的提高。进一步加入随机二值膨胀的数据增广方法之后，背包场景和穿大衣场景下的鲁棒性再次明显提升。但是这两种针对干扰问题提出的方法均对无干扰存在的普通场景下的精度带来了小幅影响。通过对HPP 结构的退化和改进，DHPP 结构大幅提升了算法的整体性能，利用仅一半左右的特征表达长度，不仅补足了之前CoordConv 方法和随机二值膨胀方法对普通模式精度的影响，算法对背包场景的鲁棒性也有了进一步提升。最后对方法进行联合训练和测试裁剪，精简了算法的结构，降低了计算量和参数量，同时再次减少了一半的特征表达长度，算法的精度并未受到严重影响，对于实际部署更加友好，最终得到的特征表达能力整体依然高于原始算法。

表8 在Casia-B 数据集下所提算法的消融实验结果Tab.8 Ablation experimental results of the proposed algorithm on Casia-B dataset

4 结论

针对实际应用中行人普遍结伴而行，造成步态轮廓提取过程中目标受到前景或后景的其他行人干扰的问题，本文提出了密集遮挡条件下的步态识别算法。本方法首先总结了此前经典的GaitSet 方法在实际应用中存在的问题。针对这些问题分别提出了解决思路。一方面通过提出基于随机二值膨胀的数据增广方法来提升算法对遮挡、背包、穿大衣等问题的鲁棒性；另一方面分析了水平金字塔池化模块的精度收益来源和局限性，根据分析结果对其进行改进，提出DHPP 结构，并引入CoordConv 方法配合联合训练策略来简化网络结构，并在保证算法精度的同时降低算法输出特征维度。实验结果表明，本方法大幅提升了步态识别算法针对密集遮挡场景下的鲁棒性，常规场景下算法整体精度相比于近几年提出的步态识别算法同样具有优势。