采用干涉条纹纹影法的轴对称温度场测量

吴军，宋丰成，潘智祥，张琛萍，郭润夏，张晓瑜

（1.中国民航大学 航空工程学院，天津 300300；2.中国民航大学 电子信息与自动化学院，天津 300300）

1 引言

航空发动机的运行状态监测在飞行安全领域发挥着重要作用［1-2］。在航空发动机工作时，尾气产生的温度场中蕴含着大量关于发动机燃烧状态的信息［3-4］。这些状态信息都可以对发动机运行状态控制提供理论依据与数据支持［5-6］。以航空发动机的尾气为例，根据火焰燃烧特性，温度分布按照中心对称并沿着空气流动方向逐渐降低形成三维温度场，采取接触式测温会破坏流场结构，影响温度测量，现阶段常用光学测量法通过测量空气折射率分布实现非接触式测温［7］。激光吸收光谱测温法是利用光在散射后发生能量衰减来对温度测量［8-10］，常适用于需要搭建大量测量结构的温度场截面测量，在尾气流场这样温度场测量中受到限制。

现代定量纹影测量技术由 Moreno-Hernández［11］提出，具有精度高，可视化效果好等优点。纹影系统结构近似为傅里叶光学处理器，使用刀口充当了空间频谱的半平面掩模，对通过待测流场的平行光束实现空间滤波，可以显示出折射率场中的纹影细节［12］。这一方法受到透镜尺寸的影响，一般测量范围在15 cm 左右，多用于实验室内测量。2013 年Martinez-Gonzalez［13］采用定标纹影法测量了加热金属板引起的空气自然对流中的温度场，2017 年，Alvarez-Herrera［14］通过改良纹影技术完成了发动机内部温度场重建。

反射式纹影技术，是20 世纪中期提出的一种将高速相机与反光屏幕和纹影技术相结合的简易纹影法。该方法早期被应用在航空弹道学和直升机旋翼的测试分析中，现在与高速相机摄像、反光屏幕等相结合进行纹影测量［15］。2017 年Gihyeon Min［16］在实验室条件 下用此方法对 蜡烛、沸腾热水壶、加热器和燃气火炬引起的空气湍流进行了成像。经过亮度补偿后，干涉精度对比原始纹影精度平均提高14.15 倍。2018 年，Martinez-Gonzalez［17］利用此方法设计了一种测量流体平面温度场的方法，并测量了商业热风枪焊接时喷嘴发出的热空气平面温度场。可以看出，与激光诊断技术［18］相结合的光学测量方法在温度测量方面具有更高的工程应用价值。结合二者优点的纹影测温方法具有非接触测量、对测量结果响应速度快和空间分辨率高的优势。由于传统的背景纹影法的局限性是测量范围基于相机的成像模型，不可避免存在图像畸变，而边缘位置图像偏移量本身较小，会导致整体测量精度的下降。本文结合纹影成像模型和激光干涉测温等原理，提出了利用干涉条纹光程差解算折射率分布的方法。该方法在保留背景纹影法测量设备简单的基础上，极大地提高了测量的稳定性与精确性。由于激光干涉条纹对折射率场变化敏感且有良好的相干性，因此产生的干涉条纹可以放大光线偏折角，进而有效提高纹影法温度测量精度。

2 干涉条纹纹影轴对称温度场测温原理

2.1 干涉条纹的形成及变形原理

条纹背景纹影法，是利用光线在通过固定狭缝后会发生的干涉现象对固定场内影响折射率分布因素的测量。

杨氏双缝干涉实验的条纹产生原理如图1 所示。相干光源S1和S2由单色点光源S垂直射到相邻的两个小孔上，此时两个小孔就相当于两个同相位的次级光源，光束在xOy平面上的成像区域叠加会产生条纹图样。这种干涉条纹是由强度相同，相位不同的光干涉产生的。

图1 两个点光源产生干涉的几何图示Fig.1 Geometric diagram of interference from a set of coherent light sources

设定干涉图样存在xOy平面上，该平面与S1S2的垂直等分线CO正交，且x轴平行于S1S2。假设两个小孔的间隔d相对于两孔连线到观察面的距离a很小，对于点成像平面上的P（x，y）而言，存在路径关系：

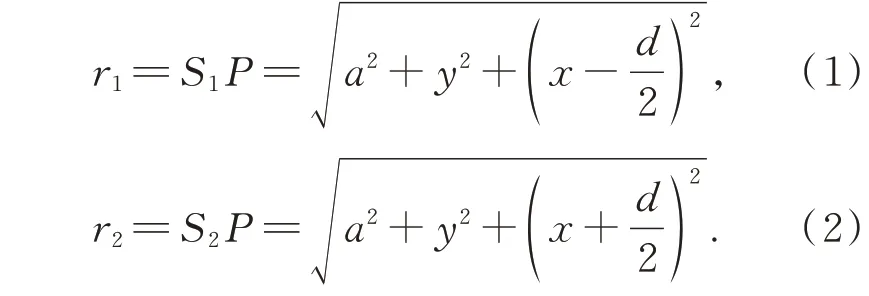
得到实际路径差：

根据温度场的变化，r1与r2路径上的折射率值发生改变，同一位置在温度场存在前后的光程差主要受到温度影响，从而改变相位差。在不考虑折射率变化的情况下有相位差关系：

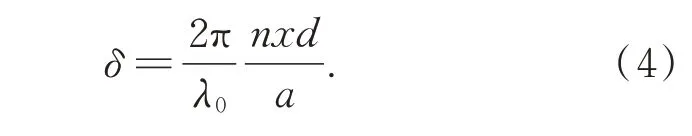
由于光在非均匀折射率场中传播时会受到介质的折射率影响改变传播速度，相干光源在经过特定的区域后，产生的相位差会发生变化。由于干涉条纹本身具有尺度的特性，在固定位置的纹影测量实验中，使用条纹干涉纹影测量的方法能够得到条纹偏移的真实距离，从而解算相位差。

条纹是根据相干光源叠加产生的，即等波长，相同传播方向，不同相位的光线叠加，可以看作两个振幅为a1的矢量波E1和E2的叠加：

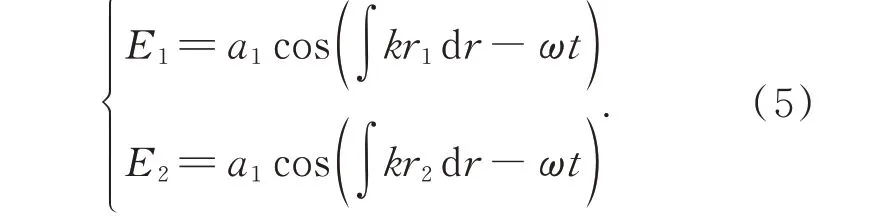
其中：ωt由于光源波长相同，频率一致，∫krdr为光线经过高温区域产生的相位变化值。

直接通过匹配光强条纹的偏移求得条纹偏移量，进而推出相位差的变化。相干光的相位变化值，可以得到光程差变化量，进而得到光路直线上折射率值的积分。

2.2 基于干涉条纹变形的轴对称温度场重构

在理想状态下，火焰温度场呈轴对称均匀分布。因此当火焰处于测量位置中心时，受到温度影响的光线折射率分布也均匀轴对称，从各个视角得到的纹影图像结果相同。假设火焰满足理想温度分布条件，就可以利用一个角度的测量信息反解出火焰的三维温度场分布。

对于轴对称的介质而言，Abel 反演公式可以实现从一维投影场重建二维平面结果。构建一个高斯分布的折射率场n，则有光线通过的积分路径如图2 所示。高斯分布的折射率场，有距离中心距离相同处折射率相同的对称特点，由于相干光线位置接近，实际产生的相位差等价于由不同的积分半径造成的积分差，其中r表示被测平面任意位置的轴向半径，R表示测量区域内的最大轴向半径。

图2 光线通过轴对称折射率场的相位差积分原理Fig.2 Principle of phase difference integration of light through an axisymmetric refractive index field

根据干涉条纹的产生性质，相位差是光程差与光频率的关系，当光线穿过轴对称折射率场时，由于光线的偏折角极小，在x处产生的相位差δ可以根据公式（8）计算：

其中的变量n为归一化折射率，即以测试场周围环境折射率为1 等比例求解的折射率分布。此归一化的折射率n分布可以由Abel 逆变换求得：

根据此公式求解积分函数时会存在奇点问题，因此求解时采用数值近似方法求解。设定两束相干光线的距离固定，且相干光线相邻两段Δr=rj-ri的相位差变化量为δj，积分得到n（ri）为不同位置的折射率梯度。变量i和j表示光线发生偏折区域的顺序数据点，即积分路径上的顺序。线性算子系数Dij与相干光线间距Δr无关系，利用反演算法可以确定：

将式（10）带入变换公式中，利用辛普森1/3rd进行求解：

带入得到线性算子系数Dij：

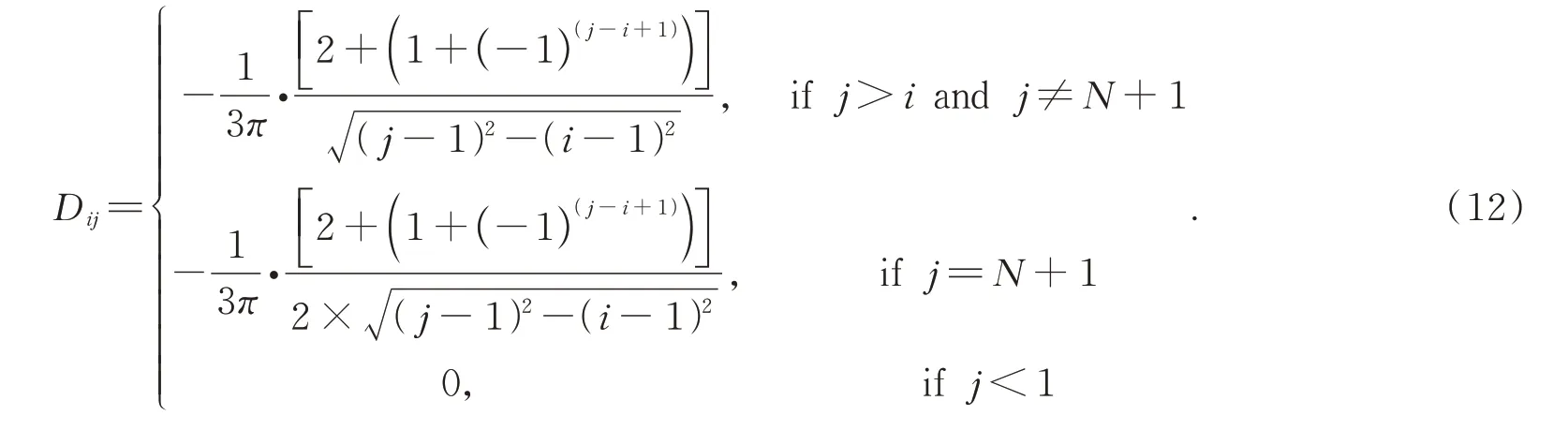
通过Dij外推后，可以得到消除i=j处的奇点，得到结果：

此时得到的Dij为相位变化值与折射率之间的关系。其中，1 标准大气压下，波长为644 nm的可见光在15 ℃且CO2含量450 ppm 的干燥空气中折射率是1.000 276 4。空气中光的折射率n受到传播介质的温度、密度以及光线的波长等条件限制，对于光线的折射率计算存在众多经验公式，符合实验室环境条件选取了Ciddor 公式［19］。将水蒸气含量百分比e=0，大气压P=101 325 Pa，光波长λ=0.54 μm，带入可以得到空气的折射率与温度之间的反比关系：

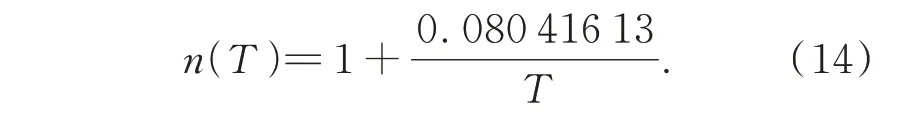
2.3 条纹系统对温度场重构的影响

图3 狭缝对于条纹影响示意图Fig.3 Diagram of the effect of slits on stripes

因为条纹图案是根据双缝干涉产生的，条纹间距反应了光程差的信息。在系统构型固定的情况下，条纹变化就可以反映该测量空间内空气折射率的变化信息，因此在固定系统构型时需要充分考虑干涉条纹的影响。由于激光干涉的特殊性质，在衍射光线夹角超过6°后，得到的干涉条纹的条纹间距就已经不能视为宽度相等，且随着条纹亮度衰减，对于不同宽度的双缝片的选取在实验中显得更加重要。在成像平面上，激光器发出的相干光的衍射效果可以近似为夫琅和费衍射，利用近似公式可以得到条纹的光强分布。当相干光线照射在宽度为d双缝上，根据惠更斯-菲涅耳原理，双缝上每个间隙都可以视为无数个新的子波源，子波源向各方向发出球面次波，这些次波在成像平面上叠加，可以得到平行于狭缝的条纹图样。a为双缝中每一条缝的宽度，λ为此激光波长。对于是夫琅和费近似，有成像平面上光强的公式［20］：

可以看出，纹影系统构型对条纹纹影法测量精度存在影响。根据公式（17），对影响成像平面上光强的变量进行仿真比较。

当波长λ=560 nm 时，对于夫琅和费单缝衍射的光线强度可以计算得出。取双缝中心对应成像平面为条纹中心，成像平面距离l+L=800 mm，对成像平面上条纹图像进行窗口为1的高斯滤波，得到不同狭缝的仿真结果如图4所示。

假设一束相干光通过（0，0）位置的双缝经过温度场，选取两组成像平面，根据公式（17）可以得到光线穿过折射率场后产生的相应的光程差，如图5 所示。

根据折射率场存在前后光程差变化，根据激光波长固定的原理，可以求解相位差，通过切面验证得到条纹偏移量结果如图6 所示。

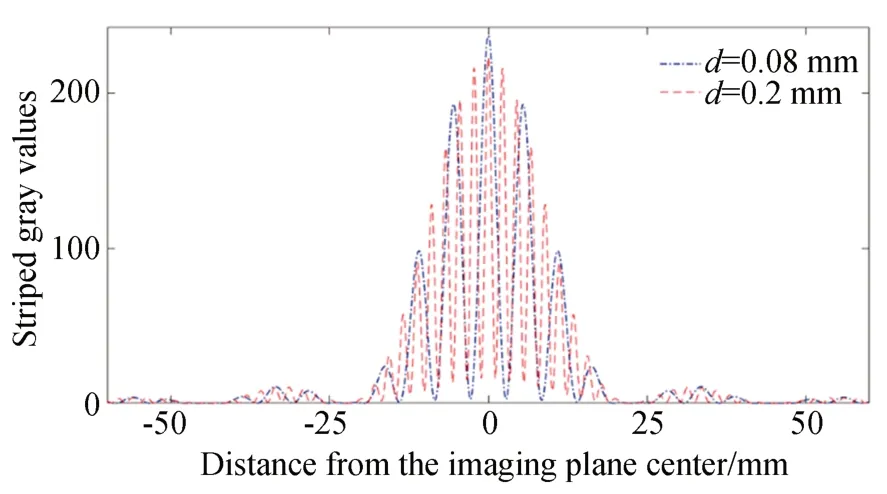
图4 不同宽度双缝衍射对应光线强度对比图Fig.4 Comparison of the light intensity corresponding to different widths of double slit diffraction

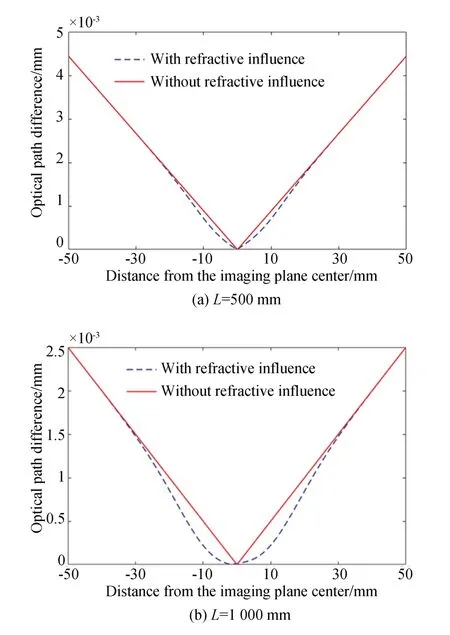
图5 不同成像平面的干涉条纹光程差Fig.5 Interference fringe optical range difference of different imaging planes

可以看出，调节干涉系统的大小对偏移结果影响成放大倍数关系。当固定双缝和成像平面的距离，调节火焰在干涉系统中位置时，条纹整体宽度无影响，但随折射率变化受到很大影响，如图7 所示，进而可以得到图8 所示的干涉条纹的偏移量。

图6 不同成像平面的干涉条纹偏移量Fig.6 Interference fringe optical range difference of different imaging planes

图7 不同火焰位置的干涉条纹光程差Fig.7 Interference fringe optical path difference of different flame positions

图8 不同火焰位置的干涉条纹偏移量Fig.8 Interference fringe offsets for different flame positions

当双缝和成像平面位置固定时，温度场距离光源越近在成像平面上得到的条纹偏移越明显。由于光线偏折角的角度很小，因此可以将光线传播路径近似为直线。由于激光传播的性质，光程差就是路径上折射率的积分。因此可以根据条纹偏移结果解算出火焰温度分布。

3 干涉条纹纹影测温的数值模拟

由2.3 节可知，不同的火焰中心温度对条纹的偏移量存在影响。设定高斯温度场火焰中心位于（1 000，0）处，双缝宽度为0.2，成像平面位于y=1 500 处（单位：mm），分别设定两组轴对称温度场，距离中心的温度如图9（a）所示，并根据经验公式求得两组温度场对应的折射率分布。

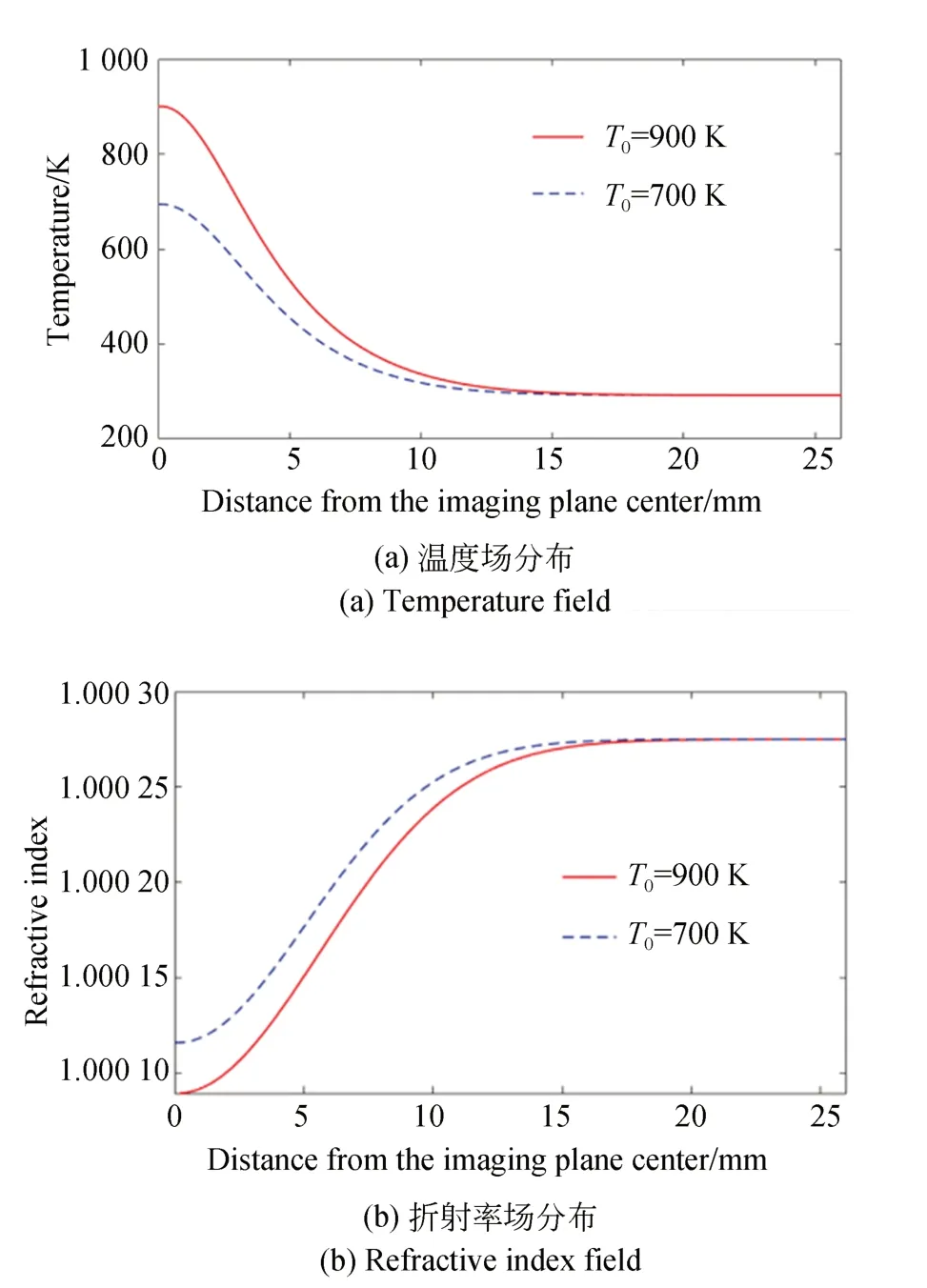
图9 数值仿真结果Fig.9 Numerical simulation

将折射率分布带入仿真程序中，可以得到不同中心温度火焰对应的干涉条纹偏移效果如图10 所示。可以看出，不同温度的轴对称场对应的折射率场不同，进而导致干涉条纹的最大偏移量位置，以及偏移量都不同。

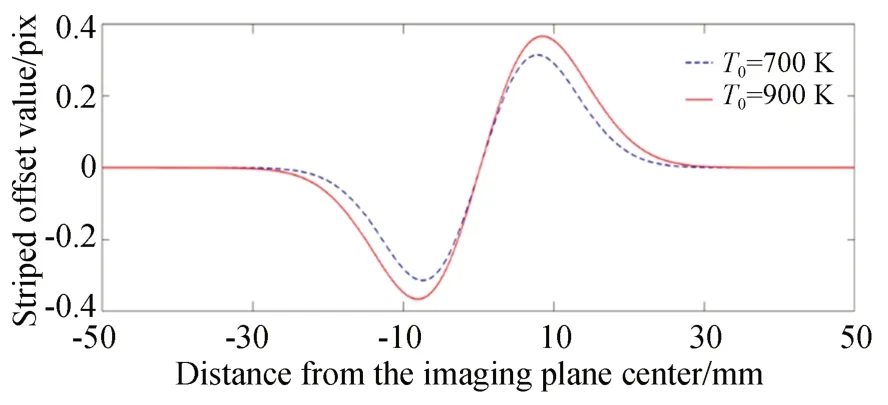
图10 不同火焰温度的干涉条纹偏移量Fig.10 Interference fringe offsets for different flame temperatures

可以利用δ（r）采用上述Abel 逆变换，可以反演求得空间中的折射率分布n（r），由于该给定温度场是标准高斯分布，选取中心角度折射率值进行对比。将中心温度为800 K 的条纹偏移量带入公式（6）中，可以计算折射率分布，径向温度分布图如图所示，由于区域范围对应实际宽度为20 mm 之内，选取200 组点进行拟合对比，结果如图11（b）所示。

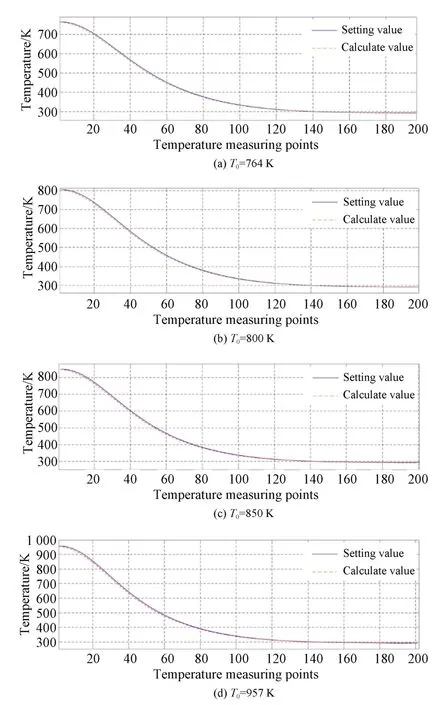
图11 不同中心温度下计算结果对比Fig.11 Comparison of calculation results at different center temperatures

分别选取4 种不同的中心温度，采用仿真方法计算条纹偏移对其产生的影响，并采用Abel 重建获得温度分布，如图11 所示。此处产生最大误差的原因是投影过程中采用了离散取值并进行的Abel 重建，反演算法时选取了边缘为可靠已知量，累计中会产生累计误差，当投影选取的离散间隔足够小时，误差可以消除。

通过图11 的数据对比，已知条纹变化量，可以得知对应温度分布中心温度。在这种温度场变化趋势固定的情况下，对中心温度多次求偏移拟合可以得到图12 所示的最大偏移量与温度的关系。因此可以根据测量得到的最大偏移量推导出中心温度。

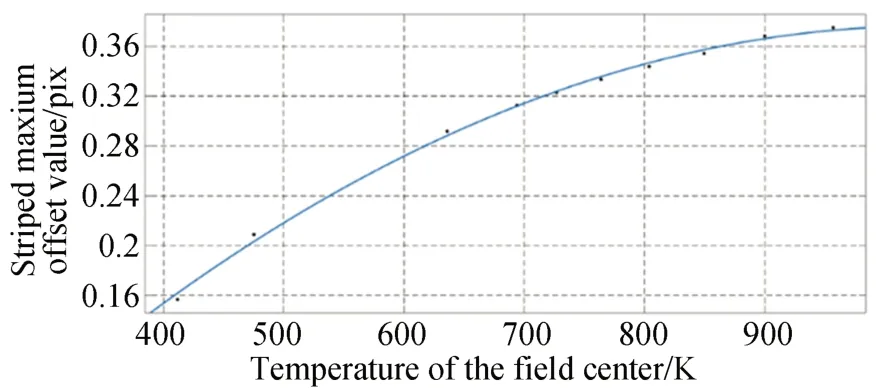
图12 条纹偏移量最大值随中心温度的变化Fig.12 Variation curve of maximum value of stripe deflection with center temperature

4 轴对称温度场条纹纹影重建测量实验

用酒精灯模拟轴对称温度场，其中由于火焰燃烧存在的不稳定性，温度真实结果是采用热电偶对火焰固定区域进行长时间测量的平均值。在实验室条件下，采用高精度铂铱热电偶（WRP-130S，测量温度范围为0～1 600 ℃）配备XMTA-308 型数字温度显示器以及高精度三坐标平移台对酒精灯火焰进行对应坐标的温度验证。利用条纹纹影法和背景纹影法同时重建酒精灯的火焰截面，辅以热电偶测得的实际温度值。搭建干涉条纹纹影测温系统如图13。

图13 实验系统图Fig.13 Experimental system diagram

在纹影系统之中，由于温度影响产生的折射率场的存在，激光器在成像平面上得到的干涉条纹会发生抖动，预先标定偏移量对激光频率造成的影响进行补偿。本实验中使用功率为50 mW的激光模组进行原理验证。如图14 所示，先进行小尺度（平面）验证，当波长为540 nm 激光时，在成像平面上得到的干涉图样条纹宽度在3 mm左右。

图14 干涉条纹图案Fig.14 Interference stripe pattern

由于50 mW 的激光经过衍射后，中央亮条纹整体亮度较高，得到条纹的光强分布曲线图15，即干扰偏移量最大值为4 pix，约单个条纹间距的10%。通过激光准直，可以精确地测量固定热电偶到火焰截面处。相机拍摄的干涉条纹由于明暗特性自身带有宽度信息。

图15 干涉条纹的灰度分布Fig.15 Grayscale distribution of interfering stripes

通过与无火焰状态下条纹光强的波形对比，利用相位角和光强成正比的关系，可以求出全部拍摄区域的干涉条纹偏移量如图16。根据推导的双缝干涉的光强公式，可以根据条纹的光强衰减变化即可求得相位差。

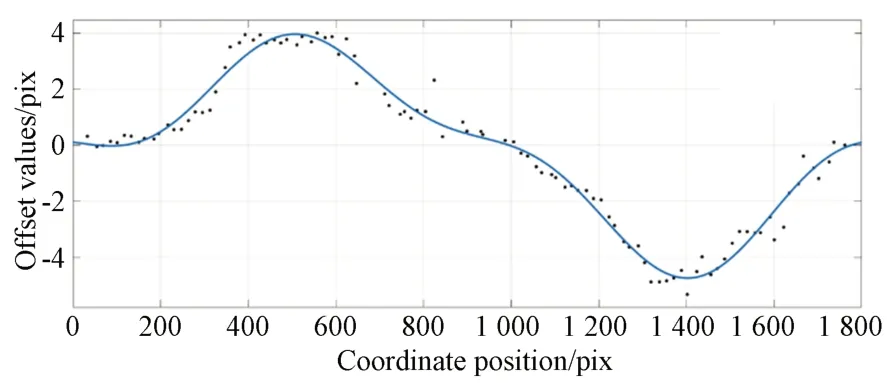
图16 干涉条纹的偏移量Fig.16 Offset of interference stripes

根据条纹的偏移量，可以积分得到归一化折射率的梯度分布，进而得到的重建温度场如图17所示。根据条纹宽度，可以确定相可以确定相机拍摄的范围为20 cm，而由于酒精灯位于狭缝和成像平面中间位置，即重建得到的火焰边界为10 cm 左右。

图17 酒精灯火焰重建温度场Fig.17 Reconstruction of temperature field by flame of alcohol lamp

采用背景纹影法重建火焰截面与此方法进行比较，如图18 所示。

实验将热电偶固定在高精度平移台上，每次沿同一方向移动5.00 mm，根据热电偶测量的酒精灯温度，和重建得到的温度场进行对比。结果如图19 所示。

图18 背景纹影测量实验场景图Fig.18 Background-Oriented Schlieren（BOS）system scene map

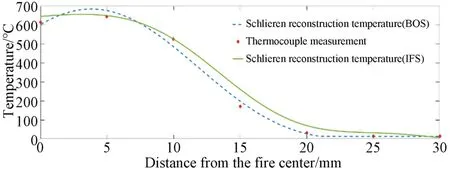
图19 酒精灯火焰重建结果图Fig.19 Alcohol lamp flame reconstruction results graph

考虑到热电偶测温存在传热不均匀的问题，整体重建结果较好。对于酒精灯火焰温度场的重建，背景纹影法平均误差为22.7 ℃，对应的测量误差范围为0.5 mm；相比条纹纹影法测量范围可达到0.2 mm，对应平均误差为15.8 ℃。

5 结论

本文详细地推导了干涉条纹纹影法轴对称温度场测温的原理，搭建了一个干涉条纹纹影系统，通过对轴对称温度场的仿真和实验，重建出轴对称火焰的温度分布。

提出了基于干涉条纹纹影系统的轴对称温度测量方法。通过相机拍摄激光干涉得到的偏移条纹信号，进而推断出待测区域的折射率场分布。利用相机的成像，与传统激光光谱测温方法相比，增大了测量区域。通过引入激光干涉，简化了传统纹影技术的复杂装置的同时，保留了纹影技术高分辨率的特点。数值模拟和对比实验的结果表明，本文提出的方法可以实现轴对称场的温度测量。在后续研究中，将进一步研究基于多角度层析重构的非轴对称温度场重构方法。