大口径主镜的六杆硬点定位机构参数优化

于致远，吴小霞，王富国

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049）

1 引言

望远镜是天文观测的工具，望远镜的性能决定了人们可观测宇宙空间的大小［1-2］。在地基大口径望远镜中，主镜的定位系统发挥了重要作用，其性能不仅关系到主镜的位姿保持精度，而且关系到主镜系统的固有频率，对望远镜的成像质量有重要影响［3-4］。大口径主镜定位系统大致可以分为以下三种类型：第一是采用实际定位点对主镜进行定位，以NTT［5］和VST［6］等望远镜为代表，在主镜的轴向和径向分别布置若干个定位点，定位点处用各种机构将主镜和镜室刚性连接，完全限制主镜的刚体位移；第二是采用虚拟定位点，以VLT［7］为代表，该方案在主镜的背部和侧面分别布置若干个液压缸，将背部的液压缸分成3个相同的扇形区域，将侧面的液压缸分为左右对称的2个区域，保持每个区域内的液压缸输出的压力相同，如此形成若干个轴向和径向的虚拟定位点，实现主镜定位；第三种是采用六杆硬点定位机构进行主镜定位，使用6 个相同结构的硬点连接主镜和镜室，不仅能实现主镜的定位，而且可以主动调节主镜的位姿。

六杆硬点定位机构是一种大型并联机构，在地基大口径望远镜中有广泛应用，例如LBT［8］、维拉·C·罗宾天文台望远镜（原名LSST）［9］、GMT［10］等。六杆硬点定位机构可以实现主镜位姿调节，无需轴向和径向定位的解耦，相比其他定位方案，六杆硬点定位在调节望远镜准直方面有明显优势，也可以应用于将大口径反射镜拼接形成主镜的方案。六杆硬点定位机构布置在主镜背部，因此主镜侧面无需布置定位机构，一定程度上简化了主镜定位系统的结构。

六杆硬点定位机构有广泛的发展前景，国内有学者开展了相关研究，胡佳宁等［11］总结了六杆硬点定位机构在国外大口径望远镜中的应用，对其结构特点和主要指标进行了对比和总结。徐宏等［12］研究了LBT，GMT 等望远镜使用的六杆硬点定位机构，总结并论述了六杆硬点定位机构的工作原理以及硬点中的位移促动器的结构特点。魏梦琦等［13］分析了六杆硬点定位机构的相关参数指标，对硬点分布半径、定位夹角、硬点长度等参数分别进行了优化。

为了将六杆硬点定位机构用于4 m 口径碳化硅主镜的定位，需要确保主镜的六杆硬点定位系统有足够高的固有频率以满足设计指标的要求。固有频率是主镜定位系统的关键技术指标，目前国际上主流的6～8 m 级望远镜，无论是采用弯月型薄主镜还是蜂窝轻量化主镜，其主镜系统固有频率普遍在15 Hz 以上，例如6.5 m 口径MMT 望远镜主镜系 统固有频率为20 Hz［14］，8.4 m 口径的LSST 望远镜 为16 Hz［15］，8 m口径的VLT 和Gemini均达到25 Hz以上［16］。

4 m 口径碳化硅主镜属于背部半封闭式蜂窝轻量化镜［17］，4 m 望远镜要求主镜系统的固有频率必须高于15 Hz 才能保证望远镜能够稳定观测，固有频率主要受到硬点的轴向刚度、主镜的质量和惯量、六杆硬点定位机构的构型参数等三个因素的影响，其中硬点的轴向刚度与硬点的结构有关，主镜的质量和惯量是由4 m 主镜的力学性质决定的，因此为六杆硬点定位机构选择合理的空间构型对于提高系统固有频率有重要意义。

为确保4 m 碳化硅主镜的六杆硬点定位机构的固有频率满足指标要求，对六杆硬点定位机构的构型参数进行了优化设计。首先对六杆硬点定位机构进行了动力学分析，推导了主镜六杆硬点定位系统的固有频率方程，建立了六杆硬点定位机构的构型参数、硬点的轴向刚度、主镜的质量和惯量与主镜系统的固有频率之间的函数关系。接着，通过有限元分析获得了硬点的轴向刚度。然后，基于固有频率方程，以最大化4 m碳化硅主镜系统的一阶固有频率为目标，使用遗传算法对六杆硬点定位机构的构型参数进行优化。最终获得了构型参数的优化结果。在最优构型参数下，主镜系统的一阶固有频率明显高于初始值，优化的效果显著，能够满足望远镜对4 m碳化硅主镜定位系统的固有频率要求。此外，还对六杆硬点定位机构在最优构型参数时的主镜系统进行了模态分析，并且校核了主镜在极限工况下的强度。

2 六杆硬点定位机构的工作原理和数学模型

2.1 六杆硬点定位机构的工作原理

六杆硬点定位机构本质上是一种大型并联机构，用于调节和保持大口径主镜的位姿，广泛用于地基大口径望远镜的主镜支撑系统。如图1所示，六杆硬点定位机构由6 个相同的硬点组成。硬点中设置有位移促动器。硬点的一端在Ai处通过柔性铰链连接到的主镜背板，另一端在Bi处连接到的镜室。主镜、硬点和镜室组成了一个类似并联平台的系统，称为主镜六杆硬点定位系统，本文简称为主镜系统。六杆硬点定位机构的原理与六自由度并联平台非常相似，调节硬点的长度的即可实现对主镜相对于镜室的位姿的调节。当保持所有硬点长度不变时，六杆硬点定位机构完全限制主镜的空间位移，实现主镜位姿的保持。

图1 六杆硬点定位机构的示意图Fig.1 Schematic diagram of six-hardpoint positioning mechanism

六杆硬点定位机构对主镜提供位姿调节和定位的功能，不用于提供支撑力，主镜的重力由多组布置在主镜背部的气压式力促动器承担，硬点理论上不受力，也不会对主镜产生力的作用。在望远镜工作过程中，由于主镜位姿改变或者惯性力、风载等因素的影响，硬点可能会出现受力的情况，此时硬点中的力传感器可以测量出力的大小，然后通过计算机进行解算，计算出所有硬点对主镜的合力和合力矩，然后通过气压促动器产生等效的校正力以抵消上述合力和力矩［18-19］。

2.2 六杆硬点定位机构的运动学模型

运动学模型是动力学建模的基础，六杆硬点定位机构的结构简图如图2 所示，图2 是图1 的简化，图2（a）表示六杆硬点定位机构处于初始位姿的状态，图2（b）表示进行位姿调节后的状态。图中O-xyz是定坐标系，与镜室固定；O1-x1y1z1是连体坐标系，与主镜固定；O2-x2y2z2是随动坐标系，其坐标原点与主镜中心点重合，各坐标轴方向与O1-x1y1z1的相应坐标轴相同。主镜作为刚体在空间中有6 个自由度，用包含6 个参数的向量q=［x y z α β γ］T表示主镜位姿，q可以分解为位置矢量t=［x y z］T和姿态矢量s=［α β γ］T。根据图3 中的几何关系可以直接得出六杆硬点定位机构的运动学逆解方程：

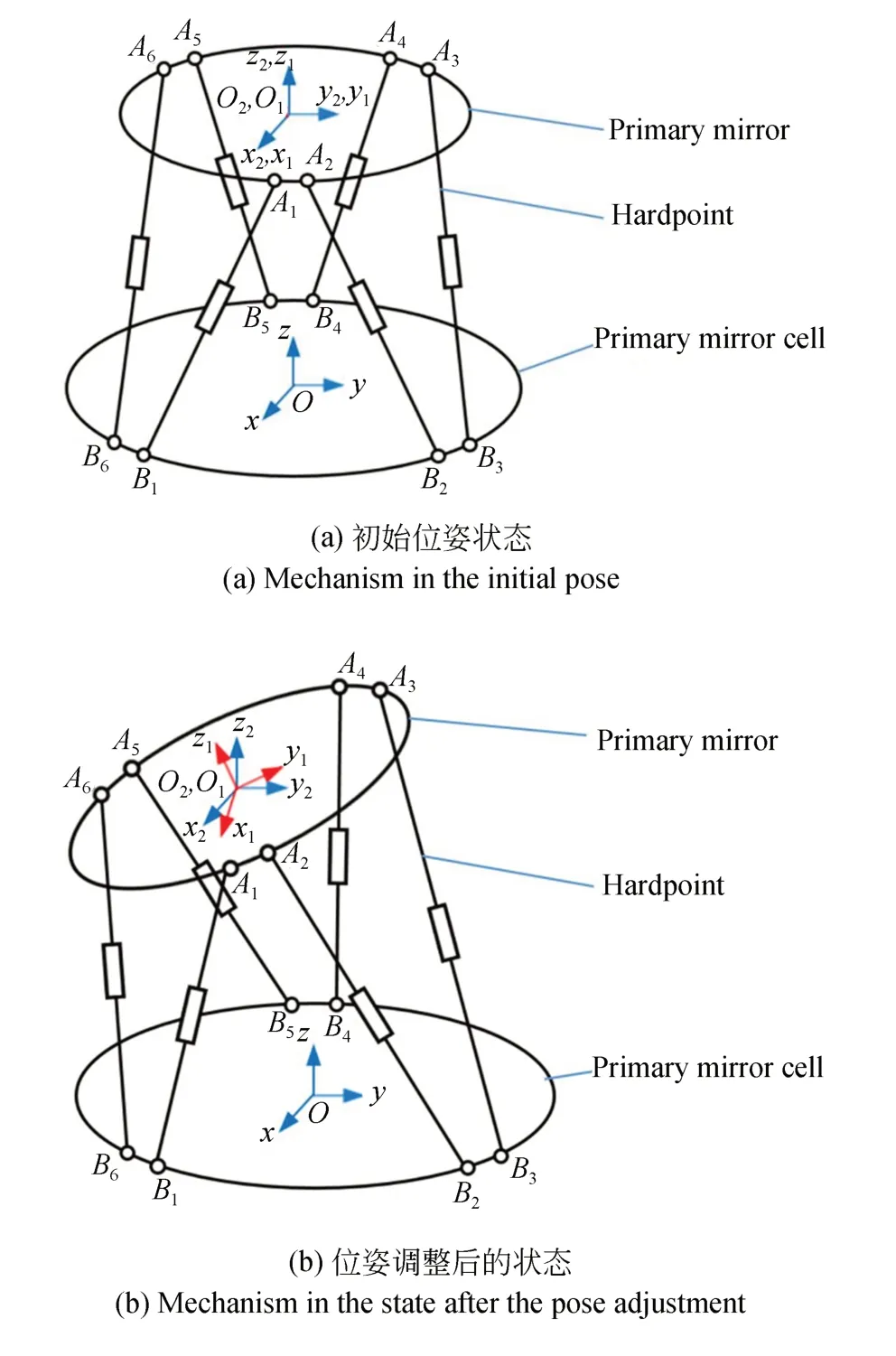
图2 六杆硬点定位机构的结构简图Fig.2 Structural diagram of the six-hardpoint positioning mechanism

其中：i=1，2，…，6，对应6 个硬点；li是硬点矢量，表示硬点的方向，硬点矢量的模是硬点的长度hi；t是主镜的位置矢量，是坐标原点O1在O-xyz中的坐标；ai是上支撑点Ai在坐标系O1-x1y1z1中的坐标，bi是下支撑点Bi在坐标系O-xyz中的坐标；R是坐标变换矩阵：

其中：α，β，γ是主镜绕坐标轴x2，y2，z2的转角，是姿态矢量s中的元素。在已知六杆硬点定位机构的构型参数的情况下，运动学逆解方程（1）给出了主镜位姿和硬点长度之间的关系。ai，bi，hi统称为六杆硬点定位机构的构型参数，通过构型参数可以确定六杆硬点定位机构的空间构型。

根据图2 中的几何关系，上支撑点Ai在定坐标系O-xyz中的坐标为：

其中：ai（O-xyz）是上支撑点在O-xyz中的坐标。定义主镜在定坐标系中的速度为q′=［t′，ω］T，ω是主镜的角速度。对式（3）求导可得上支撑点在定坐标系中的速度vai：

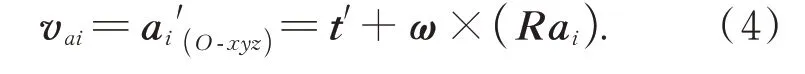
将上支撑点速度vai向硬点方向投影可得硬点的伸长速度li′：

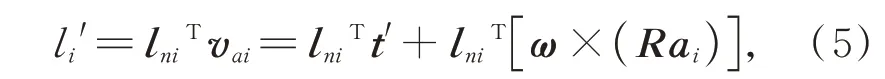
其中：lni是表示硬点方向的单位向量，表达式如式（6）所示：

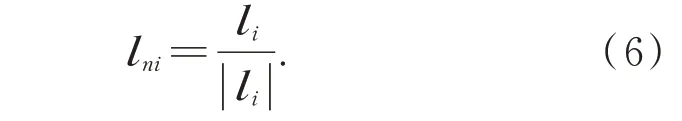
将硬点伸长速度表达式（5）写成矩阵形式为：

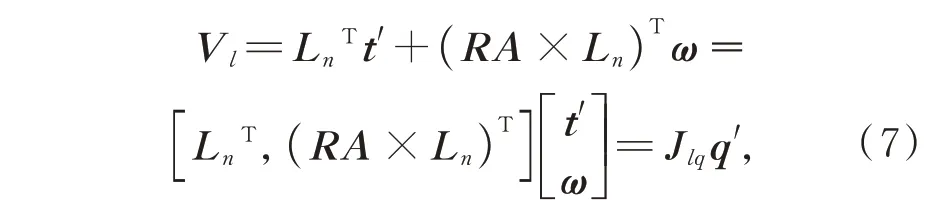
其中：Jlq=［，（RA×Ln）T］是表示主镜速度和硬点伸长速度关系的雅可比矩阵；硬点伸长速度矩阵Vl、硬点方向矩阵Ln、上支撑点坐标矩阵A的表达式如式（8）～式（10）所示：

2.3 主镜六杆硬点定位系统的动力学方程

由于硬点的质量远小于主镜的质量，因此在动力学分析中忽略硬点质量和惯性力带来的影响。此外，由于主镜的刚度远大于硬点的刚度，因此将主镜作为刚体分析，只考虑硬点的变形，不考虑主镜的变形。在这种情况下，主镜平动的动力学方程为：

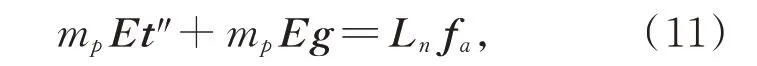
其中：mp是主镜的质量；g是重力加速度矢量；E为三阶单位矩阵；fa是各硬点对主镜的力组成的向量。主镜转动的动力学方程基于欧拉动力学方程：

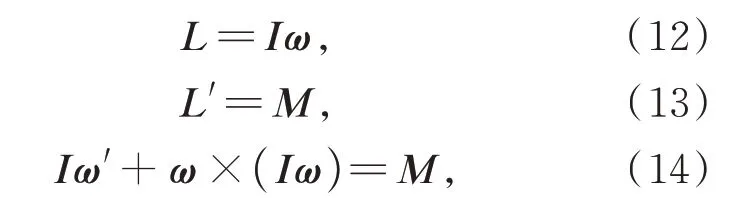
其中：L为研究对象的角动量；I是惯量矩阵；ω是角速度；M是所受的力矩。因此主镜转动的动力学方程为：

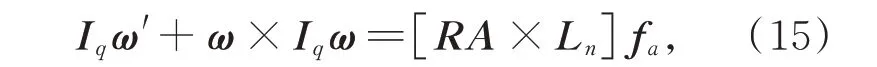
其中：Iq=RIpRT是主镜在定坐标系中的惯量矩阵；Ip是主镜在连体坐标系中的惯量矩阵。将主镜平动动力学方程（11）和转动动力学方程（15）合并为：

式（16）可以写成如下形式：

其中：M是主镜的质量惯量矩阵，C是主镜的哥氏向心项系数矩阵，G是主镜的重力矩阵。式（16）和式（17）即为主镜六杆硬点定位系统的动力学方程。

2.4 主镜六杆硬点定位系统的固有频率方程

固有频率是系统的固有属性，阻尼和外力对其没有影响，因此由式（17）得到主镜系统的振动方程为：

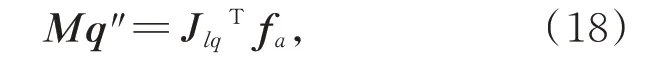
其中，fa是各硬点对主镜的力组成的向量，表达式为：

其中：K是由各硬点轴向刚度组成的对角矩阵，6个硬点的轴向刚度相同；ΔL是各硬点长度的变化量组成的向量，表达式为：

将式（19）和式（20）带入振动方程（18），得到主镜系统的运动微分方程：

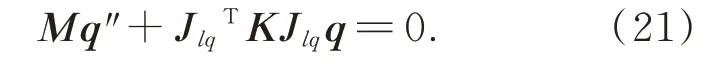
运动微分方程的特征行列式方程为：

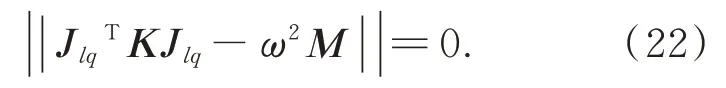
将式（22）称为主镜六杆硬点定位系统的固有频率方程，通过式（22）求解ω即可得到系统的前6 阶固有频率，单位为弧度/秒（rad/s）。可以通过式（23）进行单位换算：

其中，f是固有频率的另一种形式，单位为Hz。将Jlq和M的表达式带入主镜系统的固有频率方程（22）可得：

其中：mp是主镜的质量；Iq是主镜的惯量矩阵；K是硬点轴向刚度的矩阵；矩阵A中的元素是上支撑点的坐标；根据式（1）、式（6）、式（9），矩阵Ln由六杆硬点机构的构型参数决定。因此，固有频率方程（22）建立了六杆硬点定位机构的构型参数、硬点的轴向刚度、主镜的质量和惯量与主镜系统的固有频率之间的函数关系，可以求解系统的固有频率，也说明对于一个特定的主镜和一组特定结构的硬点，选择合适的构型参数可以使主镜系统具有更高的固有频率。综上，固有频率方程（22）可以用于六杆硬点定位机构构型参数的优化设计。

3 硬点轴向刚度计算

针对4 m 口径碳化硅主镜设计的硬点的结构如图3 所示，基于硬点的结构设计，对硬点中的元件分别进行有限元分析，计算他们的刚度，进而得出硬点的轴向刚度。如图3 所示，硬点中主要包括上柔性铰链、力传感器、扭矩限制器、分离机构、位移促动器、下柔性铰链等6 个元件，硬点的轴向刚度由这6 个元器件的刚度决定，由于所有元件的均为串联，因此硬点的刚度可以通过式（25）计算：

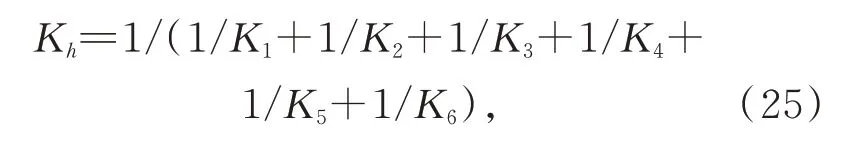
其中：Kh是硬点的轴向刚度；K1～K6分别是硬点中的6 个元件的刚度。

图3 硬点的结构示意图Fig.3 Schematic diagram of the hardpoint

在上述元件中，上柔性铰链、扭矩限制器、分离机构、下柔性铰链的结构比较简单，因此可以通过有限元分析直接计算他们的刚度，向各元件施加1 000 N 的轴向力以及相应的固定约束，得到元件的变形情况，然后通过公式计算他们的刚度：

其中：Ki表示各元件的刚度；F是轴向力的大小；Δxi是通过有限元分析得到的各元件的轴向变形量。各元件的变形云图如图4 所示，计算刚度的结果如表1 所示。

图4 硬点中部分元件的变形云图Fig.4 Deformation diagram of some elements in the hardpoint obtained by finite element analysis

表1 硬点中部分元件的轴向刚度的计算结果Tab.1 Calculation results of axial stiffness of some elements in the hardpoint

硬点中的力传感器使用Interface 品牌的1000 型轮辐式力传感器，通过查阅产品手册，得到了力传感器的轴向刚度为384 N/μm。

硬点中的位移促动器的结构相对复杂，其轴向刚度取决于促动器中的滚柱丝杠、支撑轴承、螺母座、轴套、外壳等多个元器件的刚度，促动器的轴向刚度由以下公式计算：

其中：KS和KN分别是滚珠丝杠中丝杠轴和螺母的轴向刚度，可以通过查阅产品手册获得，分别为380 N/μm 和73 N/μm；支撑轴承的刚度KB也通过查阅相应产品手册获得，刚度值为350 N/μm；KL，KZ，KW分别是螺母座、轴套、外壳的轴向刚度，均通过有限元分析获得，方法与硬点中的柔性铰链等元件的计算方法大致相同，3 个元件的变形云图如图5 所示，得到的轴向刚度分别为4 491.02 N/μm，4 300.46 N/μm，454.71 N/μm。将位移促动器中所有元件的轴向刚度带入式（27），得到促动器整体的轴向刚度为45.78 N/μm。

图5 位移促动器中部分元件的变形云图Fig.5 Deformation diagram of some elements in the actuator obtained by finite element analysis

最后，将6 个元件的轴向刚度带入式（25），得到4 m 碳化硅主镜的硬点的轴向刚度为33.044 N/μm。

4 构型参数的优化设计

基于固有频率方程（22）、硬点的轴向刚度、4 m 口径碳化硅主镜的质量和惯量指标，以最大化主镜系统的固有频率为目标，使用遗传算法对六杆硬点定位机构的构型参数进行优化。

4.1 优化目标

本文的六杆硬点定位机构构型参数优化的目标是最大化主镜系统的一阶固有频率。一阶固有频率是望远镜主镜系统最关键的技术指标之一。为了使望远镜能够稳定观测，要求望远镜有足够高的基本固有频率。而为了防止与望远镜的振动耦合，要求主镜系统的固有频率应高于望远镜的基本固有频率，一般要求至少为该值的两倍。如果固有频率低于指标要求，则振动耦合将导致成像质量降低［20］。主镜系统只有具备足够高的一阶固有频率，才能避免异常振动，保证望远镜观测稳定。因此，提高主镜系统的固有频率对望远镜的性能有重要意义。4 m望远镜要求主镜六杆硬点定位系统的固有频率高于15 Hz。

此外，由于主镜的质量和转动惯量已经确定，且硬点的轴向刚度不可能无限提高，因此主镜系统的固有频率实际上很大程度上就取决于六杆硬点定位机构的构型参数。虽然六杆硬点定位机构的运动学精度在一定程度上也受到构型参数的影响，但是相比构型参数对固有频率的影响，构型参数对运动学精度的影响很小。此外，由于硬点中位移促动器的行程较小，因此将灵巧度等指标作为优化目标的意义也不大。综上，本文最终选择将最大化固有频率作为优化目标。

4.2 优化变量及其取值范围

六杆硬点定位机构属于并联机构，其上支撑点Ai和下支撑点Bi的位置分别呈中心对称分布。用硬点的初始长度l0和支撑点的位置确定机构的构型，支撑点的位置需要4 个参数，如图6 所示，分别是上支撑点所在的圆的半径R1、相邻的上支撑点之间的夹角θ1、下支撑点所在圆的半径R2、相邻的下支撑点之间的夹角θ2。通过上述5 个参数可以完全确定六杆硬点定位机构的空间构型。2.2 节中提到将ai，bi以及硬点的长度统称为构型参数，由于ai和bi可以通过R1，θ1，R2，θ2求解，因此两种表示方法的意义是相同的。硬点初始长度的设计值为800 mm，无需优化，因此构型参数优化的优化变量为R1，θ1，R2，θ2。

优化变量的取值范围是根据结构的容许量确定的，首先注意R1和θ1，上支撑点Ai分布在主镜背板，4 m 碳化硅主镜属于背部半封闭式轻量化镜，背部有径向筋板和环向筋板，主镜背部的结构如图7 所示，为了保证主镜内部应力的合理分布，也考虑到结构的合理性，因此上支撑点Ai只能布置在径向筋板和环向筋板的交点，因此R1和θ1的取值范围如表2 所示。R2和θ2的取值范围主要考虑镜室的尺寸，初步设定R2的取值范围为350～2 000 mm，θ2的取值范围是0°～120°。此外，为了避免相邻硬点在空间尺寸上发生干涉，要求相邻的支撑点不能过于接近，因此将θ2的取值范围修正为10°～110°，同理，θ1的取值范围中的“0°”和“120°”应予剔除。

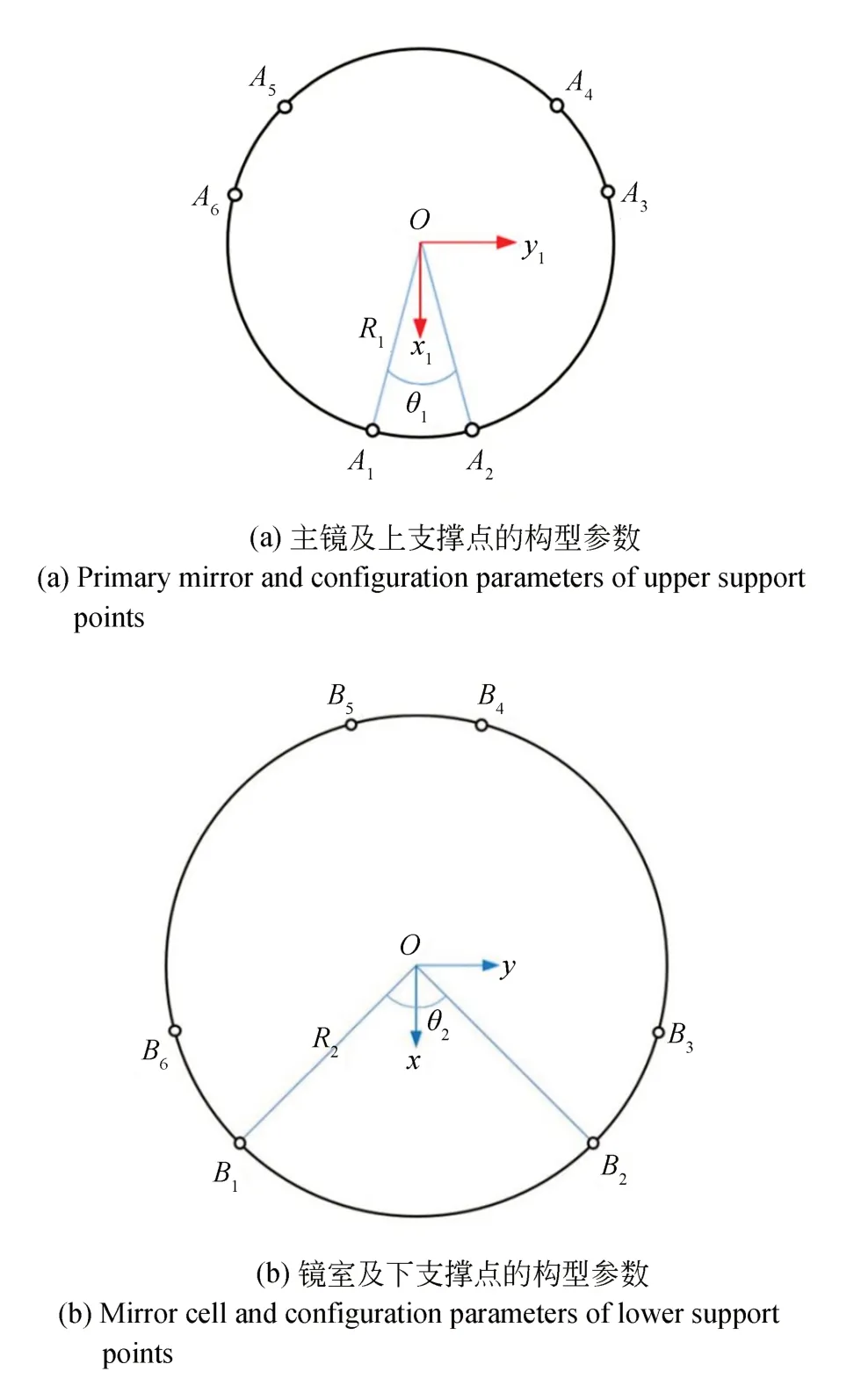
图6 六杆硬点定位机构的构型参数示意图Fig.6 Configuration parameters of six-hardpoint positioning mechanism

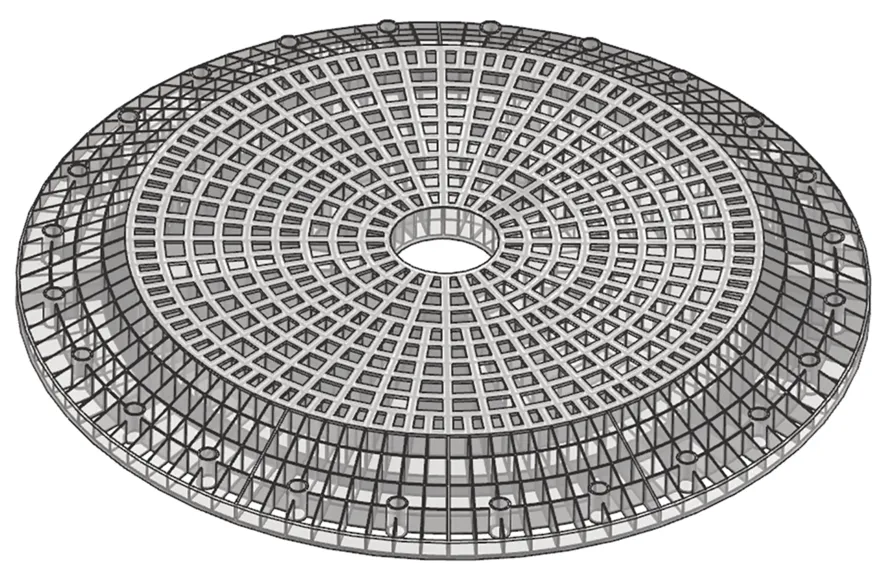
图7 4 m 碳化硅主镜的背部结构Fig.7 Backing plate of the 4 m SiC primary mirror

此外，上支撑点Ai和下支撑点Bi之间的距离在水平方向上的投影不能超过硬点的初始长度l0，因此优化变量还必须满足如式（28）所示的关系：

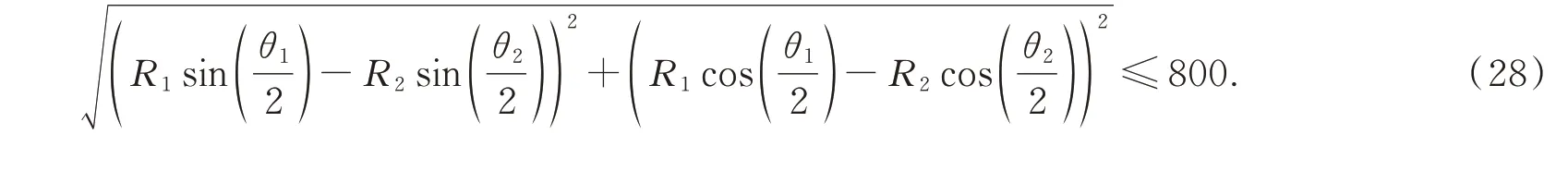
表2 上支撑点分布圆半径R1和上支撑点之间的夹角θ1的取值范围Tab.2 Value ranges of the radius R1 of the upper support point distribution circle and the angle θ1 between the upper support points

4.3 构型参数优化的方法

综上所述，本文的构型参数优化问题可表示为：

本文采用遗传算法进行构型参数优化，该算法提出于上世纪70 年代，是通过模拟生物自然进化过程搜索最优解的优化算法，其主要特点是有较好的全局搜索能力、可以自适应地调整搜索方向［21-22］。设定优化目标为最大化主镜系统的一阶固有频率，设定优化变量R1，θ1，R2，θ2及其取值范围。在优化中将硬点的轴向刚度按照第3 节有限元分析的结果设定为33.044 N/μm。此外，4 m碳化硅主镜的质量为1 684.4 kg，碳化硅材料的主要力学参数包括：密度3 050 kg/m3，杨氏模量3.92×1011Pa，泊松比0.25，将以上参数也带入优化算法。

5 结果与讨论

5.1 构型参数优化的结果

构型参数优化结果如表3 所示。通过遗传算法优化后，构型参数R1，θ1，R2，θ2的值分别为1 484 mm，30°，1 670 mm 和76°，4 m 碳化硅主镜系统在该构型参数下的一阶固有频率为30.83 Hz，能够满足4 m 望远镜对主镜系统的固有频率大于15 Hz 的要求。在遗传算法中设定的初始种群的个体数量为80，每次迭代样本数40，最大迭代次数14 次，最终产生了395 组数据。

表3 中同时列出了主镜系统在初始构型参数下的一阶固有频率，初始构型参数是根据经验初步分析选定的一组较优的参数，初始构型参数下主镜系统的一阶固有频率是14.69 Hz。将其与遗传算法得到的结果进行对比可知，在遗传算法得到的构型参数下，主镜系统的一阶固有频率相对初始参数提高了109.9%。将遗传算法得到的构型参数作为优化的最终结果，即R1，θ1，R2，θ2的最优值分别为1 484 mm，30°，1 670 mm 和76°。

表3 六杆硬点定位机构的构型参数的优化结果Tab.3 Optimization results of configuration parameters of six-hardpoint positioning mechanism

5.2 最优构型参数下的4 m 碳化硅主镜系统的固有频率计算和模态分析

分别用固有频率方程和有限元分析的方法计算4 m 碳化硅主镜系统的固有频率，对两种方法得到的结果进行对比和分析。

首先使用固有频率方程（22）计算主镜系统的固有频率，所有物理量均使用国际单位。根据最优构型参数和2.2 节的内容计算R，A和Ln，进而得到Jlq。然后基于硬点的轴向刚度值33.044 N/μm 得到矩阵K=diag（3.304 4×107，…，3.304 4×107）。4 m 碳化硅主镜的质量是1 684.4 kg，主镜的惯量矩阵Iq为：

进而得到主镜的质量惯量矩阵M=diag（1 684.4，1 684.4，1 684.4，1 659.4，1 659.4，3 283.2）。将上述物理量带入固有频率方程（22）并求解，使用式（23）进行单位换算，得到主镜系统的前6 阶固有频率的计算结果如表4 所示。由于方程（22）没有考虑主镜的变形，因此更高阶的固有频率无法用方程（22）求解。

然后，基于最优构型参数建立主镜和六杆硬点定位机构的模型，将硬点简化为杆件并设定轴向刚度为33.044 N/μm，导入有限元软件进行模态分析，得到主镜系统的前10 阶固有频率，如表4 所示。此外，还得到了系统的前10 阶模态振型，如图8 所示，图8（a）～图8（j）分别为主镜系统在最优构型参数下的1～10 阶振型，其中1～6 阶表现为主镜的刚体位移：1，2 阶为主镜的横向平移；3 阶为主镜沿光轴方向的平移；4，5 阶为主镜横向翻转；6 阶为主镜绕光轴方向的旋转，6 阶以上的振型则表现为主镜本身的变形。有限元分析的结果基本验证了前文的观点，即主镜系统的前6 阶振型体现为主镜的刚体位移，而更高阶振型体现为主镜的变形。

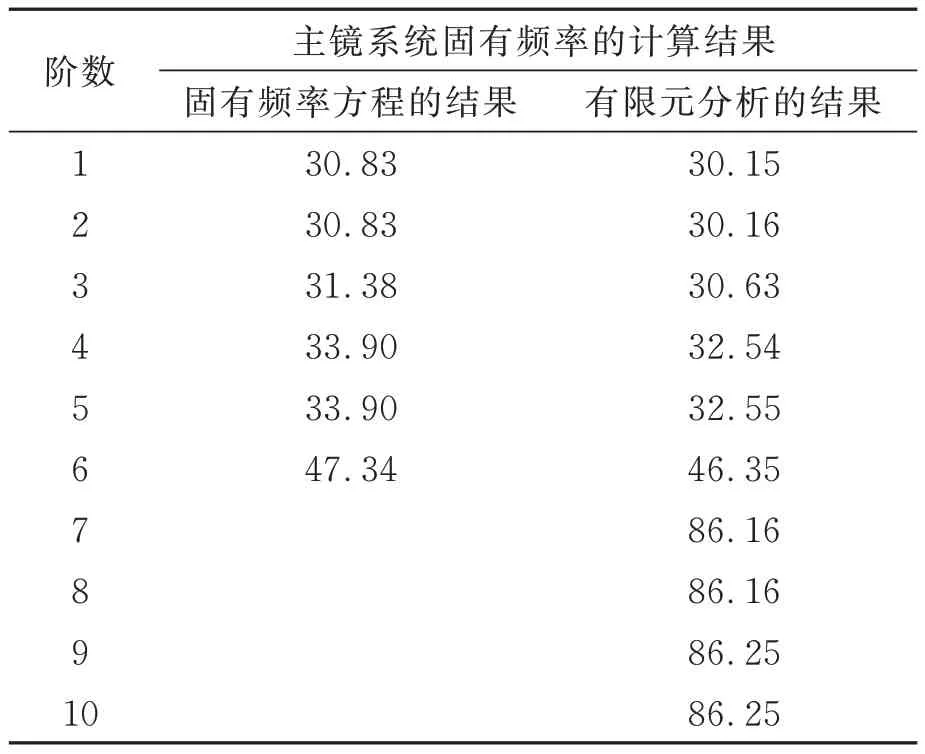
表4 主镜系统在最优构型参数下的固有频率Tab.4 Natural frequency of the primary mirror system under optimal configuration parameters （Hz）

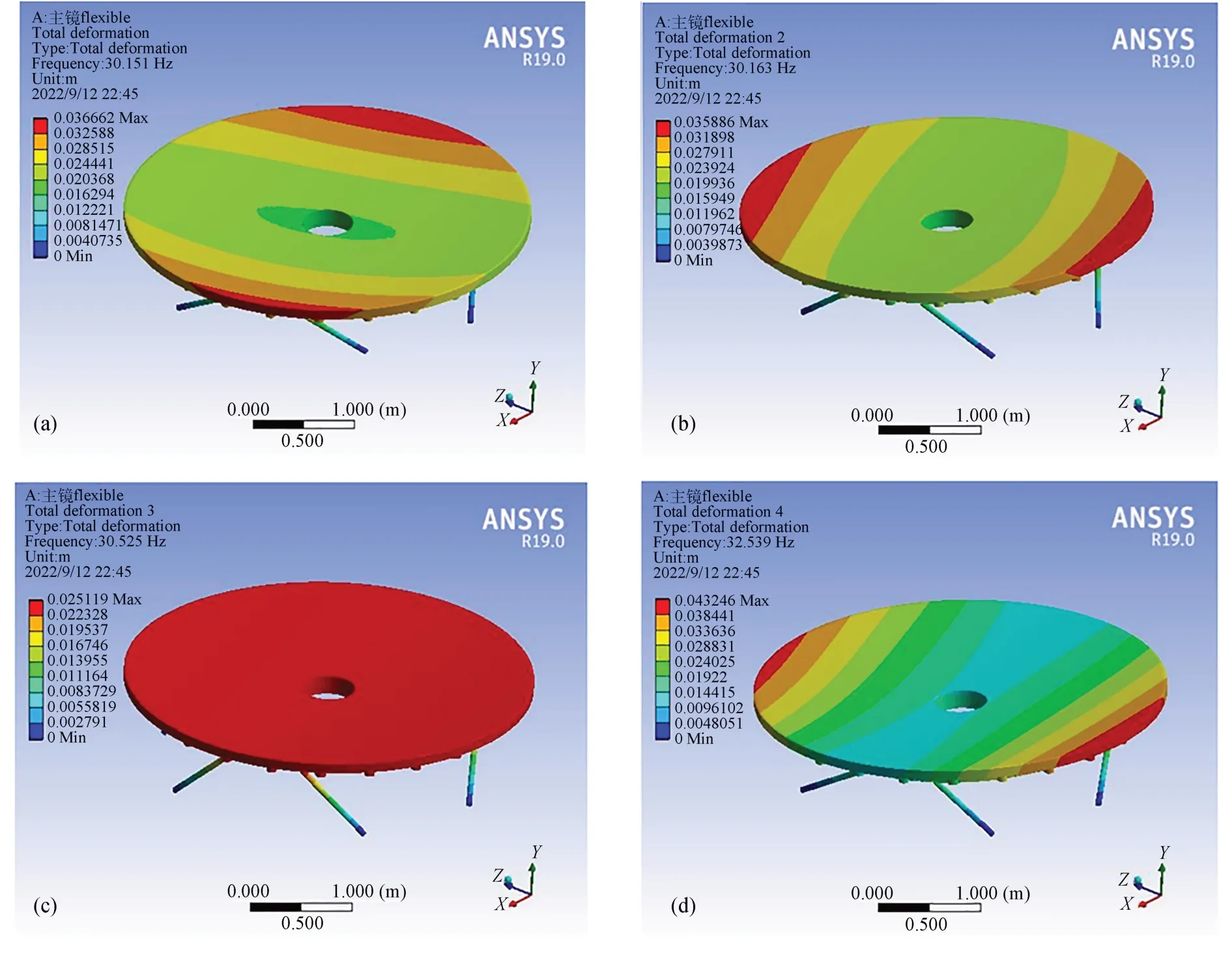
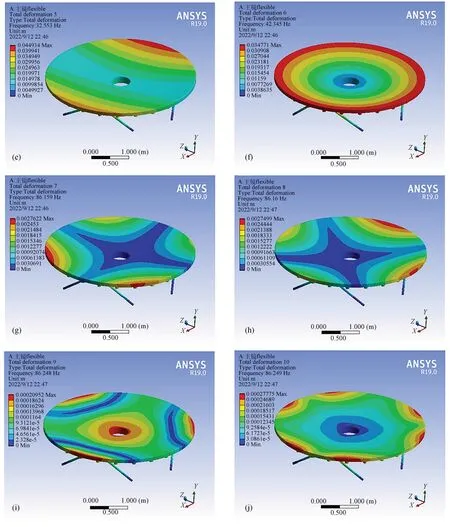
图8 4 m 碳化硅主镜的六杆硬点定位系统在最优构型参数下的1～10 阶模态振型Fig.8 First to tenth order modes of the six-hardpoint positioning system of 4 m SiC primary mirror under the optimal configuration parameters

结果表明，使用有限元计算的固有频率和通过固有频率方程计算的固有频率非常接近，说明本文推导的固有频率方程是正确的。然而表4 的结果说明，通过固有频率方程计算的结果与有限元分析的结果存在一定的误差，一方面是因为有限元分析本身存在一定的误差，另一方面是因为本文的固有频率方程没有考虑主镜的变形和硬点的质量，两个因素的共同作用导致了计算结果的误差，整体上看，误差的大小在可接受的范围内。

5.3 最优构型参数下主镜的强度校核

为了检验六杆硬点定位机构按最优构型参数排布时的主镜安全性，通过有限元分析计算了极限工况下的主镜内部应力，判断主镜是否安全。考虑到发生断电、地震等意外情况时主镜可能会因为受力过大而导致的损坏，六杆硬点定位机构中设置有安全装置，即在每个硬点中的分离装置，一旦其受力达到阈值，则可以快速降低刚度并提供一定的伸长或缩短，使得主镜落于安全防护组件上，从而保护了主镜。当硬点机构受力阈值设置为1 000 N 时，即每个硬点上施加1 000 N 的轴向力，有限元分析的结果如图9 所示，主镜中第一主应力的最大值出现在硬点与主镜的接触点处，第一主应力的最大值为0.87 MPa，该值远小于碳化硅材料100 MPa 的抗弯强度［23］。有限元分析的结果说明，六杆硬点定位机构按照本文的最优构型参数排布时，主镜在极限工况下可以保证安全。

6 结论

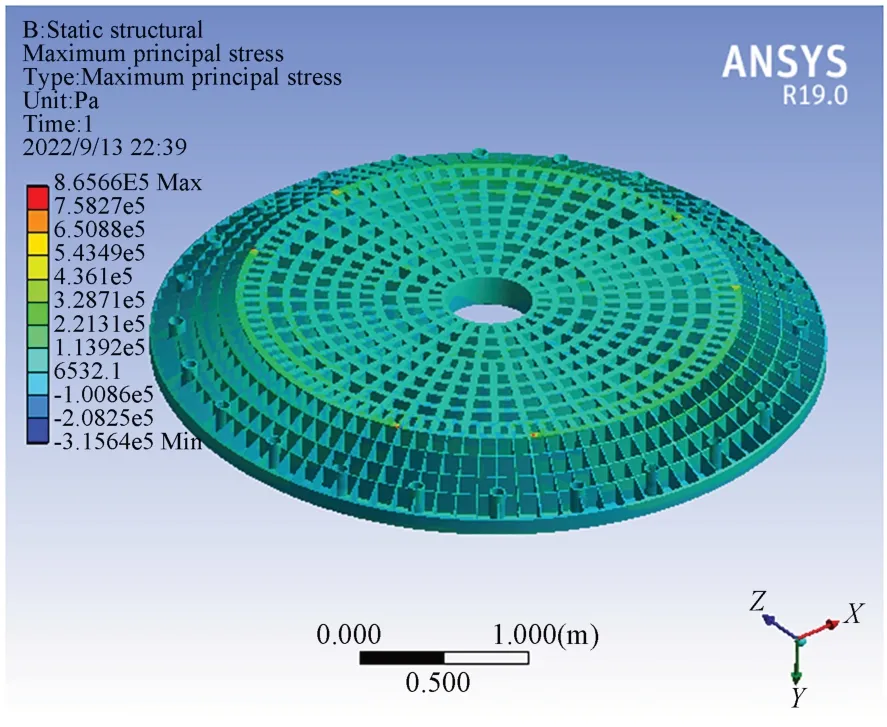
图9 主镜在极限工况下的最大主应力云图Fig.9 Maximum principal stress diagram of the primary mirror under extreme working condition

为了提高4 m 口径碳化硅主镜的六杆硬点定位系统的一阶固有频率，对六杆硬点定位机构的构型参数进行优化设计，获得了最优构型参数。首先推导了主镜系统的固有频率方程，建立了六杆硬点定位机构的构型参数与主镜系统的固有频率之间的函数关系。接着通过有限元分析获得了4m 碳化硅主镜的硬点的轴向刚度。然后基于固有频率方程，使用遗传算法对六杆硬点定位机构的构型参数进行优化。此外，还对最优构型下的4m 碳化硅主镜系统进行了模态分析。优化结果表明，构型参数R1，θ1，R2，θ2的最优值分别为436 mm，30°，600 mm 和109°，在最优构型参数下，主镜系统的固有频率达到30.83 Hz，相对初始值有较大提高，能够满足4 m 望远镜对主镜系统的固有频率大于15 Hz 的要求。本文的研究为4 m 碳化硅主镜的六杆硬点定位机构提供了最优构型参数，使主镜系统能够满足固有频率指标的要求，对保证望远镜的稳定观测有重要意义。此外，本文的构型参数优化方法可以应用于与各种口径的主镜配套的六杆硬点定位机构，为六杆硬点定位机构的参数优化提供了可行的方法。