微小磁性零件装配设备自动标定及误差补偿

任同群，江海川，张建昆，郭梦杰，王晓东

（大连理工大学 机械工程学院，辽宁 大连 116085）

1 引言

航空、航天技术的发展，对高性能微小器件的精度要求日益增高，在零件的加工精度和一致性得到保证的前提下，精密微小装配过程将直接影响零件最后的使用性能［1-2］。在装配设备搭建完成以后，由于加工误差和安装误差的存在，设备内的运动模块和测量装置等经常偏离理想位置，使后续位移转换和测量精度产生不可避免的损失，甚至导致装配失败。为了实现高精度的装配任务，往往需要复杂的运动学标定过程加以保证。

微小磁性零件装配设备集成度高、布置紧凑，整体呈现模块式的系统形式，各模块内部一般采用由精密位移滑台组成的二维或三维正交运动机构。其系统误差主要来自于模块内部滑台之间的垂直误差和不同模块对应方向滑台之间的平行误差。目前针对此类设备的标定方法，主要分为基于运动学模型的参数标定、自标定和基于神经网络的标定［3］。前两种方法都需要建立机器系统的运动学模型，但前者在进行数据采集任务时需借助外部精密测量系统，如激光跟踪仪［4-5］、激光干涉仪［6］和三坐标测量机［7］等。自标定则只需通过自身传感装置得到运动后的示数变化即可完成测量过程，进而将测量结果代入运动学模型中进行参数识别。Wang［8］借助机器视觉系统，使用九点标定方法得到了设备两个坐标系之间的转换矩阵；崔继文［9］使用CCD 相机观测辅助标记板的5 个位姿，建立了迭代二维自标定模型；谷乐丰［10］在执行器末端固定直线位移传感器，配合球杆装置建立球面约束和距离约束完成自标定中的测量任务。基于神经网络的标定方法［11-13］可以补偿系统非几何误差的影响，标定精度进一步提高，但需要大量训练样本，比较耗时。

鉴于微装配设备的结构特点，紧凑的空间设计导致外部测量装置布置困难；设备在服役期内需要定期标定，同时设备往往搭载视觉系统能够提供测量手段。因此，基于机器视觉的自标定方法尤其适合微装配设备的标定过程。但研究发现，目前采用自标定方法进行微装配设备标定时［14-16］还存在误差参数不完善、自动化程度低、时间成本高和标定精度低等问题。综上，本文针对微小磁性零件装配设备提出了一种自动标定方案及误差补偿方法。首先，考虑了Z向误差的影响，对误差参数进一步完善；其次，通过软件实现了标定流程自动化，对操作人员的要求降低的同时节约了时间成本；最后，采用粒子群算法对标定过程进行全局优化，进一步提高了标定精度。

2 误差补偿模型建立

微小磁性零件装配设备的任务是实现磁钢组件与底座的高精度自动化装配，要求装配位置精度小于15 μm，设备整体结构如图1（a）所示。设备整体呈现模块化的布置形式，按照功能的不同，可以划分为装配作业模块、视觉模块、组装工作台模块、上料手臂模块、上料台模块、上料转台模块和点胶标定模块等。将系统中的关键运动模块简化成图1（b）所示的形式，并在各模块上建立笛卡尔坐标系，其中UV表示相平面内的图像坐标系。

2.1 标定参数的确定

在执行装配任务前，磁钢组件已经被固定在组装工作台上，底座也由装配作业模块末端的夹指进行夹持。任务开始，首先控制视觉模块带动相机分别移动到底座和磁钢组件上方进行观测，接着将视觉模块的运动及相机视野中的坐标（由于相机视野有限，需要分别移动组装工作台模块和装配作业模块导轨将零件轮廓上的点通过坐标转换统一到同一坐标系中，再通过拟合算法得到两个零件的圆心坐标）向装配作业模块转换，最后控制装配作业模块导轨运动到指定位置，完成装配任务。

图1 微小磁性零件装配设备Fig.1 Micro magnetic parts assembly equipment

为了保证上述装配过程的精度，将视觉模块、装配作业模块和组装工作台模块确定为标定的对象。图1（b）中各坐标系X轴建立方向与模块X导轨一致，因而不同模块坐标系之间存在扭转偏差，各模块Y向或Z向导轨也与对应的坐标轴之间存在偏角。为了更方便地表示各模块之间的转换关系，在系统上建立世界坐标系XwYwZw，使其各轴方向与视觉坐标系方向一致。另外，相机作为测量工具，其本身的扭转偏差会对测量过程起到直接影响。同时考虑像素尺寸和Z向导轨移动对XY平面坐标的影响，归纳出需要标定的参数如表1 所示，各坐标系方向关系及误差角如图2 所示。

表1 设备标定参数Tab.1 Calibration parameters of equipment

需注意的是，该设备使用的是定焦机器视觉系统，相机与被观察件之间的距离是确定的，所以装配作业模块Z导轨夹持底座在不同高度时，视觉模块也需要运动到相应高度进行观察。因此，将视觉模块Z导轨与装配作业模块Z导轨之间的夹角（实际为两模块Z导轨移动时特征点位置相对于移动距离的比例变化关系）作为标定参数，不进行视觉模块Z导轨本身倾斜的标定。

2.2 运动转换模型推导

运动转换的基本思想是不考虑坐标系原点位置，只关注坐标系和导轨方向性的影响，进行相对位移之间的转换。

将世界坐标系作为模块之间的运动转换中介，建立各模块导轨与世界坐标系之间的运动转换关系，为后续装配过程作铺垫。转换矩阵由各模块坐标系与世界坐标系之间的旋转矩阵和各模块坐标系与自身导轨之间的补偿矩阵结合而成。

在推导过程中将运动转换分成XY平面和Z方向两部分进行讨论。

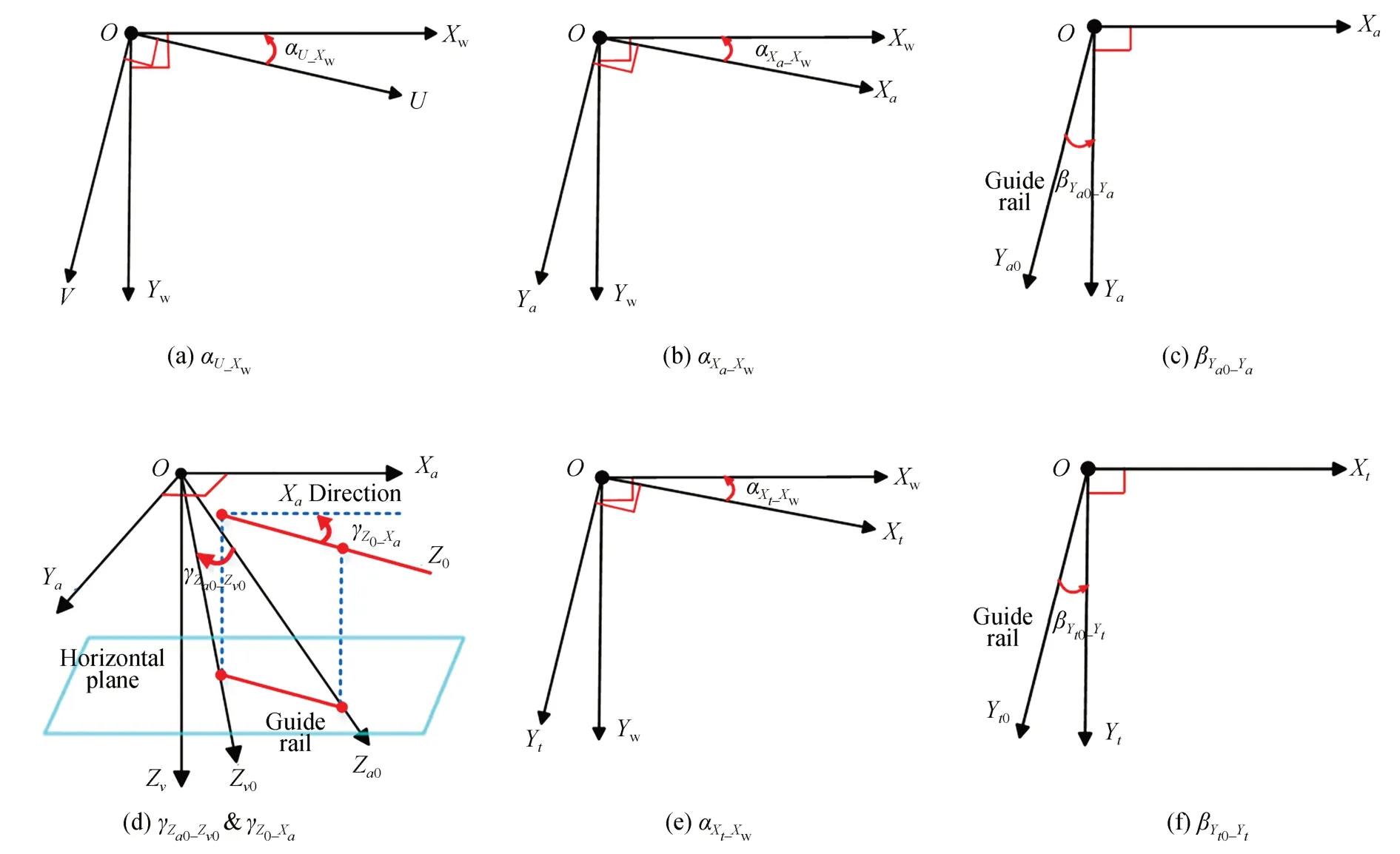
图2 坐标系及误差角示意图Fig.2 Schematic diagram of coordinate system and error angle

在XY平面内，由于视觉模块没有Yv0导轨（设定其虚拟的方向与Xv0导轨垂直），且视觉坐标系和世界坐标系均以视觉模块Xv0导轨作为建系基准，所以视觉模块导轨的相对运动和世界坐标系中的运动是相同的，如式（1）所示。“Δ”表示相对坐标，以下公式中意义相同。

图像坐标系和世界坐标系之间是简单的旋转关系，同时考虑像素尺寸转化的影响，如式（2）所示：

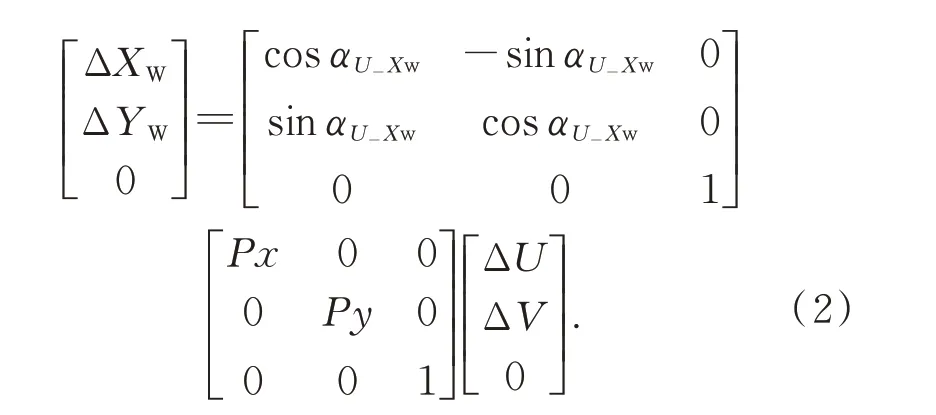
将世界坐标系中的相对坐标向装配作业模块导轨的运动进行转换，如式（3）所示；相应地，将装配作业模块导轨的运动向世界坐标系中的相对坐标进行转换，如式（4）所示：

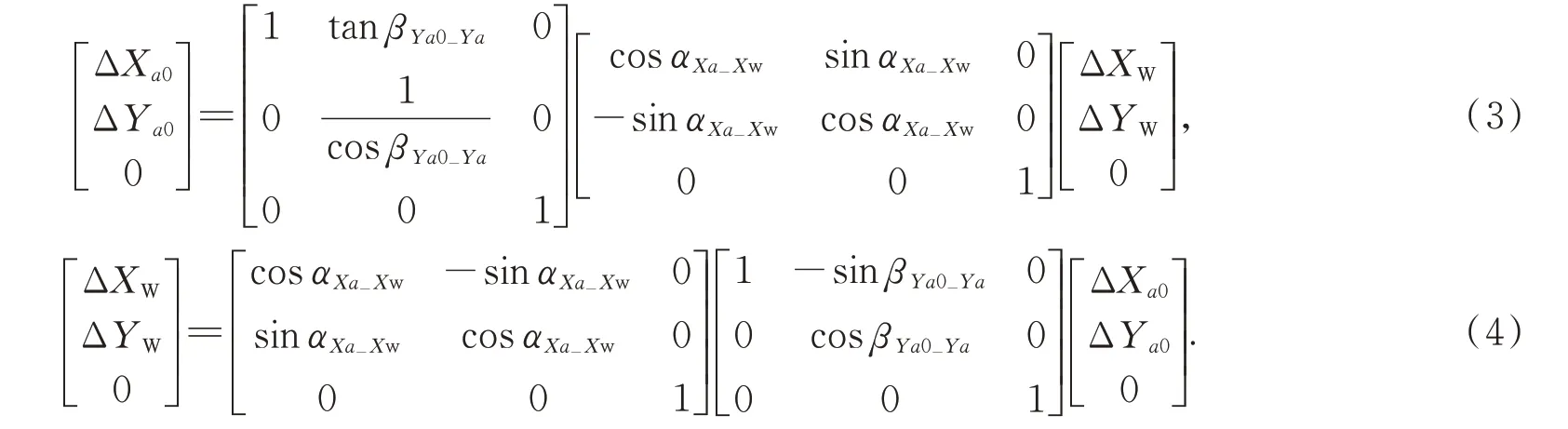
组装工作台模块导轨与世界坐标系之间的转换关系和装配作业模块在XY平面内与世界坐标系之间的转换关系类似，更改成对应角度即可。

在Z方向，由于没有将视觉模块Z导轨本身的倾斜作为标定参数，而标定了视觉模块Z导轨与装配作业模块Z导轨之间的夹角，所以这里将视觉模块Z导轨的运动直接向装配作业模块导轨转换，如式（5）所示：

2.3 基于装配任务的误差补偿模型推导

基于上述装配过程的描述和推导的运动转换模型，首先从XY平面和Z方向两个方面分别讨论误差补偿过程，最后整合成统一的误差补偿模型。

在XY平面内，先将两个零件在图像坐标系内的坐标差值和视觉模块导轨的运动转换到世界坐标系中，如式（6）所示；再将世界坐标系中的位置差转换到装配作业模块的导轨运动中，如式（3）所示。

在Z方向，直接将视觉模块Z导轨的运动向装配作业模块导轨转化，如式（5）所示。

进一步将式（3），式（5），式（6）进行整合，得到基于装配任务的误差补偿模型，如式（7）所示。

3 误差参数标定原理

3.1 线性标定原理

在进行误差线性角度标定时，基本思想是：将标定板固定到需要标定的模块上，控制相应导轨进行运动，并观察运动前后标定板上特征点在相机视野中的位置变化，最后将运动信息和坐标信息代入理论模型中计算，即可得到误差角。

在进行X向角度标定时，以世界坐标系Xw轴与组装工作台坐标系Xt轴夹角αXt_Xw标定过程为例，如图3 所示。

将标定板固定在组装工作台模块上，视觉模块移动到其上方；通过图像处理得到标定板上的特征点A在图像坐标系中的V向坐标n1；然后两模块X导轨同时向正方向运动L 脉冲，特征点A在图像坐标系中的V向坐标变化为n2，B点代表两模块X导轨平行时特征点的理论坐标，由图3中的几何关系可得：

图3 X 向误差角度标定Fig.3 Error angle calibration in X direction

在进行图像坐标系和世界坐标系之间的夹角αU_Xw标定时，标定板固定不动，需要视觉模块带动相机观察标定板上两个已知距离的不同特征点；在进行Y向角度标定时，由于视觉模块没有Y导轨，所以视觉模块保持不动，需要移动组装工作台模块或装配作业模块Y导轨，同样通过相机观察两个已知距离的不同的特征点。后续计算过程类似，不作过多赘述。

在进行Z向角度γZa0_Zv0标定时，标定模型如图4 所示。将标定板固定到装配作业模块上，视觉模块移动到其上方，通过图像处理得到标定板上的特征点A在图像坐标系中的形心坐标A1（m1，n1）；接着两模块Z导轨同时向正方向移动，装配作业模块运动了L脉冲，视觉模块运动后重新聚焦共运动了L1脉冲，重新观察特征点A的坐标A2（m2，n2），C点代表两模块Z 导轨平行时运动后的理论坐标。

经过分析发现，我们需要的是两导轨运动时误差随导轨运动距离的变化关系，因此这里将两模块Z导轨之间的夹角γZa0_Zv0重新定义，如式（10）和（11）所示，令：

再由图4（b）可得两模块Z导轨同时运动引起的误差变化方向与装配作业坐标系Xa轴夹角：

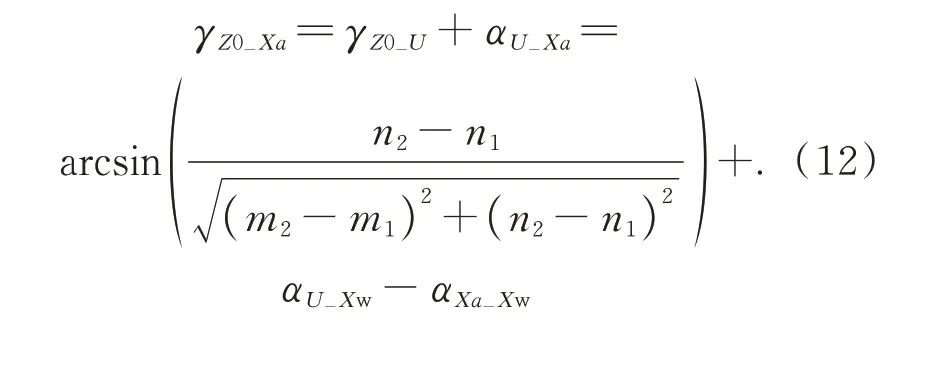
图4 Z 向误差角度标定Fig.4 Error angle calibration in Z direction

3.2 全局优化原理

经过分析，上述线性标定方式中还存在误差传递和累积的显著问题：由于各参数在标定过程中具有一定的顺序性，如组装工作台坐标系与世界坐标系X轴夹角αXt_Xw在求解过程中会用到图像坐标系与世界坐标系夹角αU_Xw、所有角度标定都会用到像素值Px和Py等。当前置参数出现标定误差时，必然会将误差传递到后续参数的计算中，造成误差累积现象。

为了进一步提高设备定位精度，需要对基于装配任务的误差参数进行全局优化，得到适用于整个装配区域的最优参数。粒子群算法（Particle Swarm Optimization，PSO）是一种模仿鸟群觅食行为的智能优化算法，通过群体中个体之间的协作和信息共享来进行迭代，适用于多元函数的最优解求解问题；与其他优化算法相比，PSO具有调节参数少、收敛速度快等优点［17-19］。因此，尝试使用粒子群算法进行误差参数的全局优化。

粒子群算法的标准流程可以描述为：

（1）对粒子群进行初始化，这其中包括种群规模、速度范围、惯性权重和学习因子等参数的设置；

（2）对各粒子的适应度进行计算，得到粒子的个体极值和群体极值，其中适用度值由适用度函数进行计算，适应度函数需要根据优化问题进行自行设置；

（3）根据公式（13）和（14）对粒子的速度和位置分别进行更新：

其中：i表示第i个粒子，j表示 粒子的维数；t表示迭代次数；ω表示惯性权重，用于提高粒子的收敛速度，一般取0.5～1；c1和c2表示算法的学习因子，c1用来使粒子趋向个体最优位置，c2用来使粒子趋向全局最优位置，一般取值0～2；r1和r2为［0，1］中的随机数；vij（t）为第t次迭代时粒子i的当前速度，需要根据实际问题对其范围进行设置；xi（t）为第t次迭代时粒子i的当前位置；pbestij（t）表示个体i的当前最优极值，gbest表示整个粒子群的最优极值；

（4）再次进行适应度函数计算，并对粒子的个体极值pbestij（t）和群体极值gbest进行更新；

（5）根据终止条件进行判断，若满足条件则计算终止；若不符合要求，则重回步骤（3）继续进行迭代，直到满足要求。终止条件需要根据实际情况进行设置，可以是精度要求或迭代次数等。

根据上述原理，使用粒子群算法对误差参数的线性标定过程进行了优化设计：

（1）粒子设置。基于装配任务，将式（7）中的7 个误差参数设置为七维的粒子：

（2）在装配区域内进行坐标采集。装配作业模块夹持标定板，视觉模块带动相机观察到标定板上的一个特征点，分别控制视觉模块和装配作业模块沿各自导轨方向运动相同的脉冲数（由于视觉模块没有Y向导轨，所以在进行Y方向位移时仅装配作业模块运动），记录下视觉模块运动脉冲数［ΔXv0ΔYv0ΔZv0］T、特征点在图像坐标系中的坐标变化［ΔUΔV0］T和装配作业模块运动脉冲数［ΔXa0ΔYa0ΔZa0］T。如图5 所示（彩图见期刊电子版），为了更好地及整个区域，选择面对角线AB，AC，AD以及一条体对角线AE 作为采集路线，按照上述过程控制两模块在红色点位上运动，得到12 组运动数据。

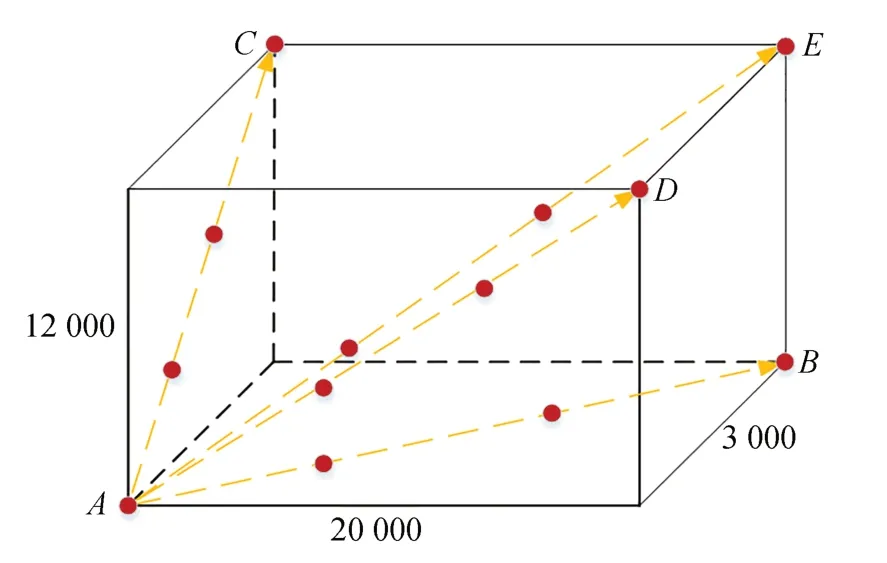
图5 装配区域采集点位置Fig.5 Collection point location in assembly area

（3）结合误差补偿模型，进行适应度函数设计。将粒子代入到式（7）的等式右边，结合上述运动过程中采集的数据进行计算，得到等式左边装配作业模块的运动计算值［ΔXΔYΔZ］T，将其与采集数据中的实际值［ΔXa0ΔYa0ΔZa0］T进行比较，计算各方向误差的平方差之和，再将12组数据的误差相加作为该算法的适应度函数，如式（15）所示：

（4）寻找最优解。设置合适的参数和种群数，通过多次迭代，将最终error 最小的一组粒子作为优化后的标定参数。

4 标定实验及验证

根据标定任务设计了多用途的标定板及其在装配作业模块和组装工作台模块上的固定结构，如图6 所示。标定板委托“深圳清溢光电股份有限公司”制作，工艺为湿法刻蚀。中间细方框线宽的设计尺寸是500 μm，出厂前对其线宽进行检测，均匀的选取了10 个测量位置，精度检测结果如表2 所示，其制造误差在1 μm 以内。标定板的设计要考虑从以下两方面：一方面，标定板的整体及特征尺寸需要与模块末端结构大小及相机视野范围相匹配；另一方面，标定板上的图案包含了所有参数标定过程中的需求特征，同时可进行标定结果的验证工作。

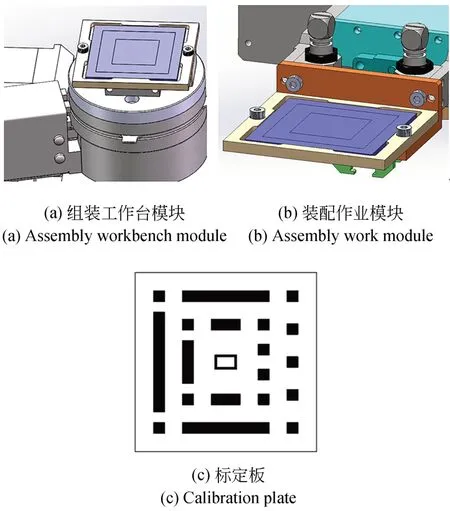
图6 标定装置结构图Fig.6 Calibration device structure diagram

表2 标定板检测结果Tab.2 Calibration plate test result （μm）

4.1 标定实验

基于.NET 平台开发了自动标定软件，对标定过程中的运动、误差角的计算以及标定结果的保存等进行了封装，并设计了如图7 所示的标定顺序，实现了“一键式”的标定效果。除手工装夹和更换标定板位置之外，所有标定过程均自动进行，降低了对操作人员的技术要求；同时整个标定流程可在6 min 内完成，极大提高了标定效率。

将标定板分别固定在组装工作台模块和装配作业模块上，借助设备中的光学显微视觉系统进行自动标定实验，标定现场如图8 所示。

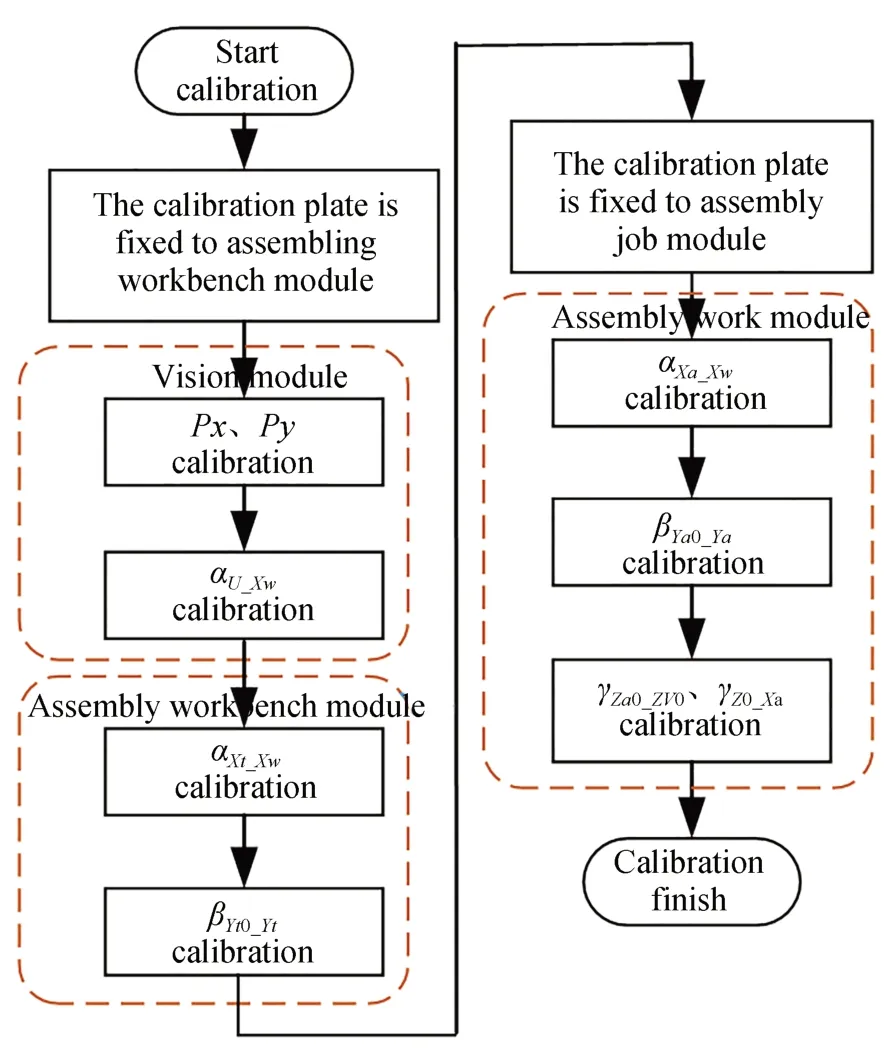
图7 标定流程Fig.7 Calibration process

图8 标定实验Fig.8 Calibration experiment

在装配区域内进行标定实验，受标定板图案尺寸及导轨行程的影响，确定组装工作台模块的标定范围为28 000 μm×21 000 μm（2 个自由度），装配作业模块的标定范围为40 000 μm×37 000 μm×15 000 μm（3 个自由度），均在包含装配区域且大于装配区域的范围进行。标定结果如表3 所示。

针对表3 中与装配过程相关的7 个参数进行粒子群优化。首先在20 000 μm×3 000 μm×12 000 μm 的装配区域范围内，进行了如图5 所示的12 组运动数据的采集；对粒子群算法的各类参数进行确定，根据经验及如表4～表5 采取控制变量的对比实验方法得出，以相邻适应度函数error之间的差值是否小于10-6μm 作为迭代收敛的判断标准，在总体测试时间可接受范围内，选取平均误差（定义如式（16）所示）更优的参数值：取种群粒子数N为1 000，迭代次数t为100；惯性权重ω为0.5；学习因子c1和c2为2；根据误差参数本身的大小设置了各自的速度和位置范围；为了克服粒子群算法容易陷入局部最优的缺陷，同时加快其收敛速度，采用前述线性标定的结果对粒子进行了初始化。经过粒子群优化后的标定结果如表6 所示。

表3 标定结果Tab.3 Calibration results

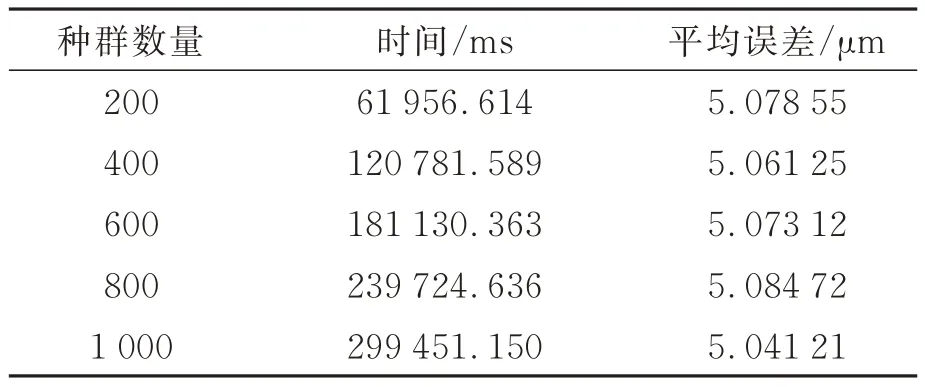
表4 粒子群种群数量对比实验Tab.4 Population comparison experiment of PSO

表5 粒子群学习因子对比实验Tab.5 Learning factor comparison experiment of PSO

表6 粒子群优化后的标定结果Tab.6 Calibration results after PSO

4.2 标定结果验证

将标定板固定到装配作业模块上，移动各模块导轨，使标定板上某个特征点出现在相机视野中，当视觉模块和装配作业模块沿各自导轨运动后会引起特征点的坐标变化。选择4 个不同方向的矢量位移［10 000，2 000，0］T，［10 000，0，8 000］T，［0，2 000，8 000］T，［10 000，2 000，8 000］T作为验证路径（如［10 000，2 000，8 000］T表示视觉模块X导轨和Z导轨分别运动10 000 μm 和8 000 μm；装配作业模块X，Y和Z导轨分别运动10 000 μm，2 000 μm 和8 000 μm），控制视觉模块和装配作业模块导轨在装配区域内不同位置沿着上述路径各随机运动了6 次，记录下特征点在图像坐标系中的实际坐标变化（ΔU，ΔV）；分别使用优化前和优化后的误差参数，配合运动转换关系，计算理论上运动后的坐标差值（ΔUT1，ΔVT1）和（ΔUT2，ΔVT2）；使用式（17）和（18）分别计算未优化的结果与实际的偏差E1和优化后的结果与实际的偏差E2。

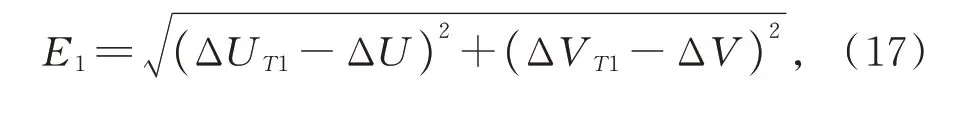
实验结果如图9 所示。

图9 粒子群优化前后验证数据对比Fig.9 Comparison of validation data before and after PSO

对优化前后误差的均值和极值进行计算，如表7 所示。

从图9 和表7 可以看出，线性标定方法中通过线性路径标定出的参数在整个装配空间内适用性较差，经过粒子群算法优化后的标定模型有效降低了误差累积的影响，标定出的参数更具有全局适用性；且验证得到的误差补偿模型在整个装配空间内的定位精度在6 μm 以内，符合装配任务要求。

同时图（a）中的实验现象也表明，在XY平面内（图（a）中的验证路径属于XY平面），线性标定的误差要略优于粒子群全局优化后的误差。这主要是因为，在线性标定中XY方向上的参数是在XY平面内标定得出的，没有Z方向运动的影响，在该平面进行验证时只引入了XY平面内的运动误差；而粒子群全局优化的标定参数是通过整个装配空间求最优解得到的，在XY平面进行验证时，除该平面内的误差，也间接引入了Z向运动误差的影响。

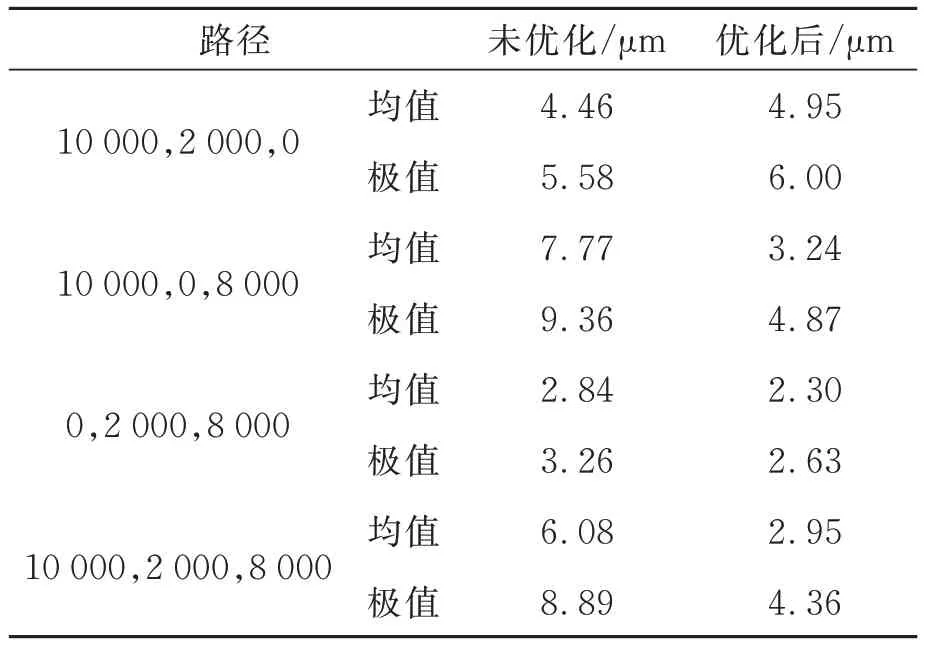
表7 粒子群算法优化前后误差比较Tab.7 Comparison of errors before and after PSO

表8 装配实验Tab.8 Assembly experiment

将标定的数据代入2.3 节中的误差补偿模型，进行8 次装配实验，结果如表8 所示。受装配策略及零件磁力等因素的影响，装配后的磁钢组件及底座的位置精度有所波动，但都在精度允许范围内，证明了标定参数的精确性及该标定方法的有效性。

5 结论

本文针对微小磁性零件装配设备提出了一套自动标定及补偿方法。首先根据设备结构特点建立各模块坐标系，确定了对装配任务产生影响的误差参数，并推导了各模块与世界坐标系之间的运动转换模型和基于装配任务的误差补偿模型。然后基于机器视觉和专用的标定板，提出了误差参数标定原理，并给出了通过粒子群算法对参数进行全局优化的方法。最后进行了线性标定实验和粒子群优化实验并进行了精度验证。

实验结果表明，经过粒子群优化后的标定方法使系统开环控制精度在6 μm 以内，满足了磁钢组件与底座的装配精度要求。同时，该方法还具备了自动化和高效率等优点。本文提出的标定方法也具有通用性，可以微调后用于同类微装配设备的标定工作。不仅如此，基于机器视觉的自标定方法也为导轨之间平行度和垂直度的测量提供了一种简单易行的思路。