基于离散元法的颗粒饲料粘结参数标定及其破碎过程分析

■王 雷 张永林 李 彬 路婉秋 杨 柳 刘晓鹏

（1.武汉轻工大学机械工程学院，湖北武汉 430023；2.武汉轻工大学动物科学与营养工程学院，湖北武汉 430023）

饲料是养殖业的基础，可为动物生长、生产提供所需营养保障[1-2]。传统的饲料加工成型方法主要有两种：制粒和膨化。制粒饲料（颗粒饲料）因具有避免动物挑食、报酬率高、流动性好、便于管理等优点，在家禽养殖生产过程中得到了广泛应用[3-8]。制粒饲料（颗粒饲料）是由粉状原料在制粒机内经水热调质、机械挤压聚合成型，因其表面粗糙度较大、物料成分之间的聚合力较小，导致颗粒饲料在筛分、喂料、输送、喷涂、干燥、包装等加工环节中，易因加工机械内部的挤压、剪切而发生破碎，从而造成营养成分损失、颗粒饲料品质降低[9-10]。由于难以通过实际试验对颗粒饲料在各环节加工机械内部的运动与受力状态进行实时监测与分析[11-14]，颗粒因机械力而产生破碎的机制尚不明确，因此，难以有针对性地对加工机械的关键结构、运行参数进行优化，改善颗粒饲料的受力特性，从而有效降低其破碎率。

离散元法是研究离散单元之间的互作关系的方法[15]。随着计算机仿真技术的发展，该方法现已在分析颗粒的运动规律、受力状态、参数标定等方面得到广泛应用[16-17]。彭飞等[18]探究了饲料调制器中饲料的运动规律，并采用计算流体动力学与离散元耦合的方法对调质器的工作过程进行仿真建模和作业参数优化。殷洁鑫等[19]对蛋鸡饲料破碎度进行了研究和评定，通过优化旋刀破碎机刀片的旋转速度，降低了破碎物中的含粉率。刘晓鹏等[20]开展了漏斗法和提升法的颗粒状饲料动、静态流动堆积过程分析，并根据二次正交旋转组合仿真试验对颗粒状饲料的离散元接触参数进行了标定。彭飞等[21]提出了一种基于注入截面法的休止角测定装置与方法，对颗粒饲料的离散元接触参数进行了标定。曹丽英等[22]应用离散元法和流体仿真耦合法，分析了物料颗粒在锤片式饲料粉碎机内的运动轨迹。综上分析，应用多用途离散元素法建模软件EDEM仿真可较真实地模拟颗粒的各项物理特性，但在该方法的应用上，鲜有针对颗粒饲料破碎方面的研究。

本研究针对颗粒饲料在加工过程中易发生破碎，且因破碎机制尚不明确，难以通过优化加工机械的关键结构、运行参数来降低颗粒破碎率的实际问题，以母猪颗粒饲料为研究对象，采用原颗粒聚合法（颗粒之间通过Bonding键连接）建立离散元仿真模型，结合台架试验对仿真模型的粘结参数[单位面积法向刚度（Kn）、单位面积剪切刚度Kt）、临界法向刚度（Cn）、临界剪切刚度（Ct）]进行测试与标定，并解析颗粒饲料的破碎过程，以期明确颗粒饲料在受力状态下的破碎过程，为优化加工机械的关键结构及运行参数、降低颗粒破碎率提供理论依据。

1 材料与方法

1.1 颗粒仿真模型

以武汉海大饲料有限公司生产的母猪颗粒饲料为研究对象（见图1a），反复测试可得其基本尺寸参数：平均直径为4.5 mm，平均长度为9 mm。应用Solidworks 软件建立与饲料形状尺寸相符的三维模型，在EDEM软件中采用原颗粒聚合法对三维模型进行填充，如图1b 所示。所填充的球形颗粒之间通过Bonding 键粘结聚合一体，Bonding 键的力学属性是影响该仿真模型抵抗破碎力的关键因素，该力学属性主要取决于4个粘结参数：单位面积法向刚度（Kn）、单位面积剪切刚度（Kt）、临界法向刚度（Cn）、临界剪切刚度（Ct），可按公式（1）计算[23]：

图1 饲料样品及其离散元仿真模型

式中：Fkn、Fkt——分别为法向挤压力、剪切力（N）；

Fknmax、Fktmax——分别为最大法向挤压力、最大剪切力（N）；

Δxn、Δxt——分别为挤压位移、剪切位移（mm）；

Sn、St——分别为当量挤压接触面积、当量剪切接触面积（mm2）；

Snmax、Stmax——分别为最大受力状态时的挤压接触面积、剪切接触面积（mm2）。

1.2 台架试验

根据式（1）可知，为确定粘结参数，需确定颗粒所受挤压、剪切作用时的力、位移、受力作用面积等参数。其中，挤压力、剪切力、位移可应用质构仪开展剪切与挤压试验获取，受力接触面积则采取图像染色处理的方法进行估算。

1.2.1 挤压与剪切试验

应用TA.XTC-18型质构仪（上海保圣实业发展有限公司）开展颗粒饲料的挤压和剪切试验，如图2a、图2b所示。取200个三轴尺寸相同的颗粒饲料为试验对象（挤压试验100个，剪切试验100个），设置圆柱压头的下压速度分别为0.1、0.2、0.3、0.4、0.5 mm/s，剪切压头的下降速度分别为0.6、0.8、1.0、1.2、1.4 mm/s，挤压与剪切位移均为4.5 mm，每组试验均重复20次。试验可分别获取“Fkn—Δxn”曲线、“Fkt—Δxt”曲线，如图2c、图2d所示。通过该曲线可获取最大法向挤压力（Fknmax）、最大剪切力（Fktmax）。上述曲线线性阶段的斜率可表示为：

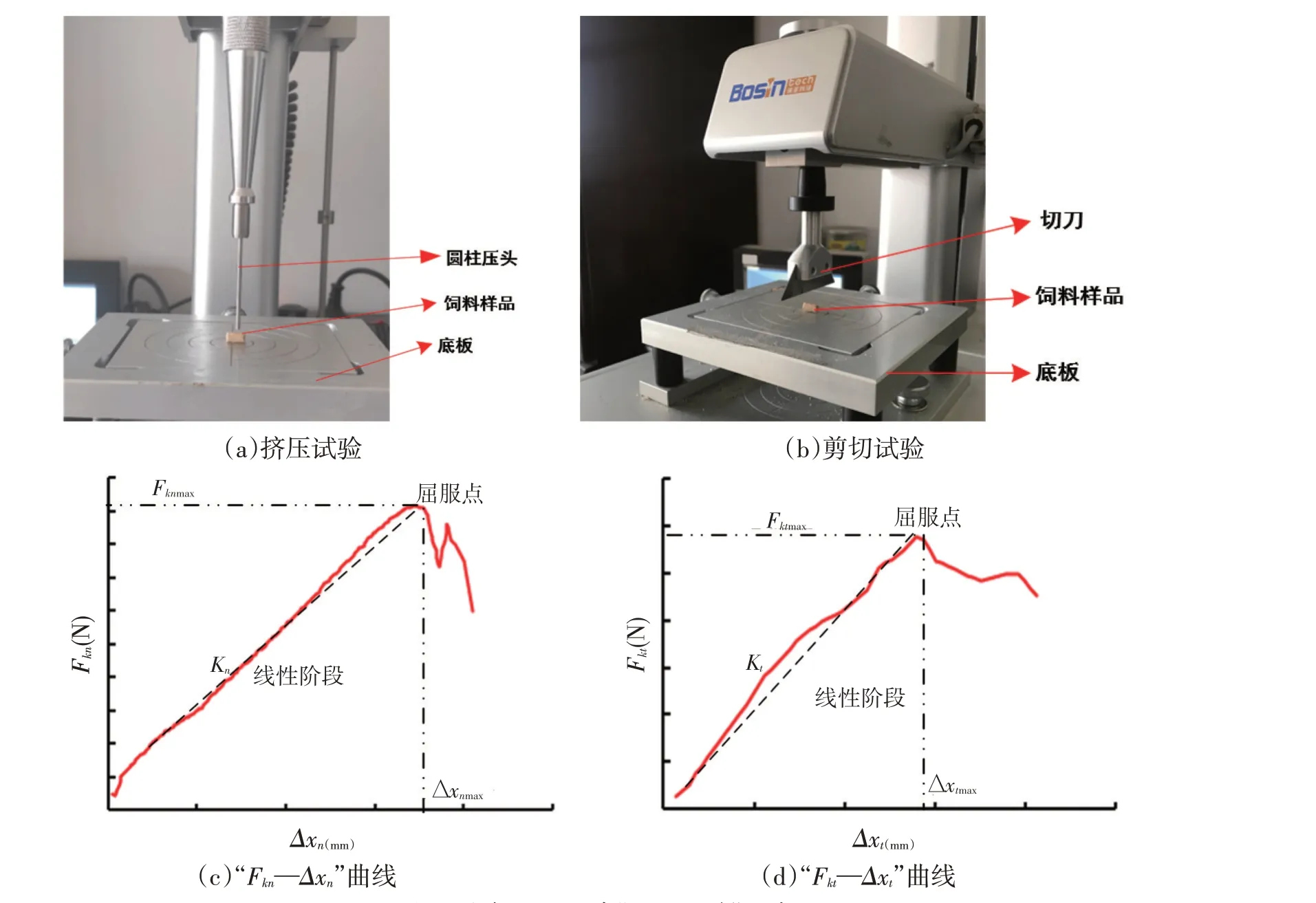
图2 台架试验及其“力—位移”曲线

式中：kn——“Fkn—Δxn”曲线线性阶段的斜率；

Kt——“Fkt—Δxt”曲线线性阶段的斜率；

Δxnmax——分别为受最大挤压力时的压头位移（mm）；

Δxtmax——分别为受最大剪切力时的压头位移（mm）。

1.2.2 接触面积估算

将圆柱压头（直径2 mm）底部（粘贴薄纸片）、切刀压头（厚度0.4 mm）刃口侧部均涂有红色染色墨水。当饲料样品处于最大挤压状态时，圆柱压头与饲料样品完全接触，故圆柱压头截面积即为此时的挤压接触面积Snmax；根据前文所得“Fkt-Δxt”曲线，设置切刀压头的剪切位移为Δxtmax。将刚好切断的饲料样品取出，应用Super eyes 图像设备（深圳超眼科技有限公司）采集染色图像，并在Image J软件中分析计算光滑断面的染色面积。试验重复5 次，取均值即为最大受力状态时的剪切接触面积Stmax。

挤压、剪切的当量接触面积，则需在每次挤压、剪切试验前（试验重复5次），手动调节圆柱压头位置与饲料样品刚刚接触、切刀压头刃口与饲料样品刚刚贯入。采用与前文相同方法对每组试验的染色面积进行分析计算，记录每组挤压、剪切试验的染色面积分别为：{sn1、sn2、sn3、sn4、sn5}、{st1、st2、st3、st4、st5}。染色试验如图3所示。饲料样品的当量挤压接触面积、当量剪切接触面积取值范围为：

图3 染色试验

1.3 EDEM仿真试验

根据式（1）、（2）、（3）可计算出临界法向刚度（Cn）、临界剪切刚度（Ct），但单位面积法向刚度（Kn）、单位面积剪切刚度（Kt）只能确定其取值范围。本研究通过开展EDEM 仿真试验对Kn、Kt进行标定。在EDEM 软件中按实际比例建立如图4 所示仿真模型。参阅参考文献[18，20]，仿真相关参数如表1 所示。选择Kn、Kt为试验因素，开展二因素五水平的二次回归正交旋转组合试验，试验水平编码为-1.68、-1、0、1、1.68。试验指标为挤压、剪切台架试验与仿真试验的综合误差（δ），表示为：

表1 离散元仿真参数

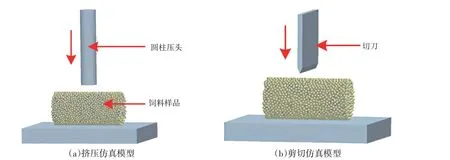
图4 EDEM仿真模型

式中：F′knmax、F′ktmax——仿真试验的最大法向挤压力、最大剪切力（N）。

2 结果与分析

2.1 挤压试验

对不同压速的试验数据Fkn求平均值，试验结果如图5 所示。试验结果表明，不同压速下测得的“Fkn—Δxn”曲线没有明显的差异，表明压速对挤压试验结果没有显著的影响。根据式（2）计算得到不同压速曲线线性阶段斜率（kn），可知kn值波动不大；不同压速的20 次试验的屈服值平均值（Fknmax）以及破坏时挤压位移基本一致，kn值、Fknmax均值如表2所示。

图5 不同压速的“Fkn-Δxn”曲线

表2 kn、Fknmax测试结果

2.2 剪切试验

与挤压试验分析中一致，对不同剪切速度的试验数据Fkt求均值，试验结果如图6 所示。试验结果表明，不同剪切速度的“Fkt—Δxt”曲线没有明显差异，表明剪切速度对挤压试验结果没显著影响。由式（2）得到不同剪切速度曲线线性阶段斜率kt值，剪切速度的20 次试验的屈服值的平均值（Fktmax）变化不大，kt值、（Fktmax）均值如表3所示。

表3 Kt、Fktmax试验结果

图6 不同剪速的“Fkt—Δxt”曲线

2.3 粘结参数计算与估算

当饲料样品处于最大挤压状态时，圆柱压头与饲料样品完全接触，因此Snmax即为圆柱压头的截面积，取值为3.14 mm2；通过不同压速挤压、剪切染色试验可得，饲料样品的当量挤压接触面积、当量剪切接触面积、最大受力状态时的剪切接触面积如表4 所示。根据式（1）计算不同压速下临界法向刚度、临界剪切刚度的均值：Cn=2.93×107Pa，Ct=2.22×106Pa。

根据不同压速的挤压、剪切染色试验可得，当量挤压接触面积（Sn）取值为2.22～3.14 mm2、当量剪切接触面积（St）取值范围为3.22～5.11 mm2。根据表2中kn、Fknmax的取值及式（1）、（2）、（3），可得单位面积法向刚度（Kn）取值为4.09×1010～5.78×1010N/m3，由此预估单位面积法向刚度Kn的量级范围为[1010,1011]。根据表3 中Kt、Fktmax的取值及式（1）、（2）、（3），可得单位面积剪切刚度（Kt）取值为4.8×109～8.93×109N/m3，初步确定单位面积法向刚度（Kt）的量级范围为[109,1010]。

2.4 仿真标定

通过开展二次回归正交旋转组合试验对单位面积法向刚度（Kn）、单位面积剪切刚度（Kt）进行标定。以Kn、Kt为试验因素，以式（3）计算得到的综合误差为试验指标。试验水平及编码如表5所示，试验设计与结果见表6。

表5 试验因素编码（N/m3）

表6 二次回归正交旋转组合试验设计与结果

应用Design-Expert 8.0.6.1 软件对试验结果进行方差分析，结果见表7 所示。方差分析结果表明，二次全模型P＜0.01，应用二次模型方程拟合效果较好，模型决定系数R2为95.47%。通过二次多元回归拟合的回归模型如图7所示，回归方程为：

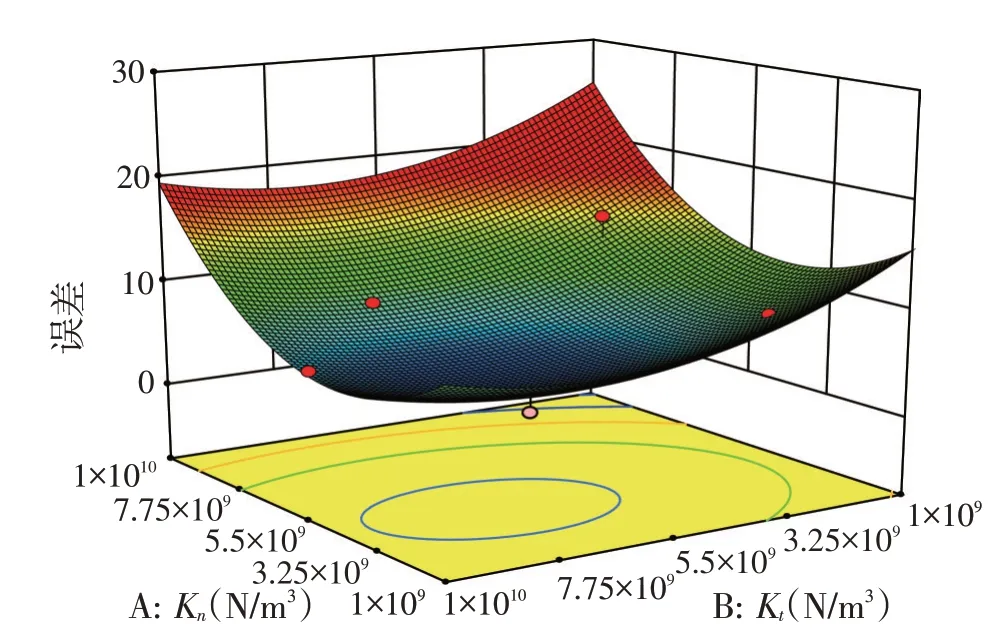
图7 回归模型响应面图

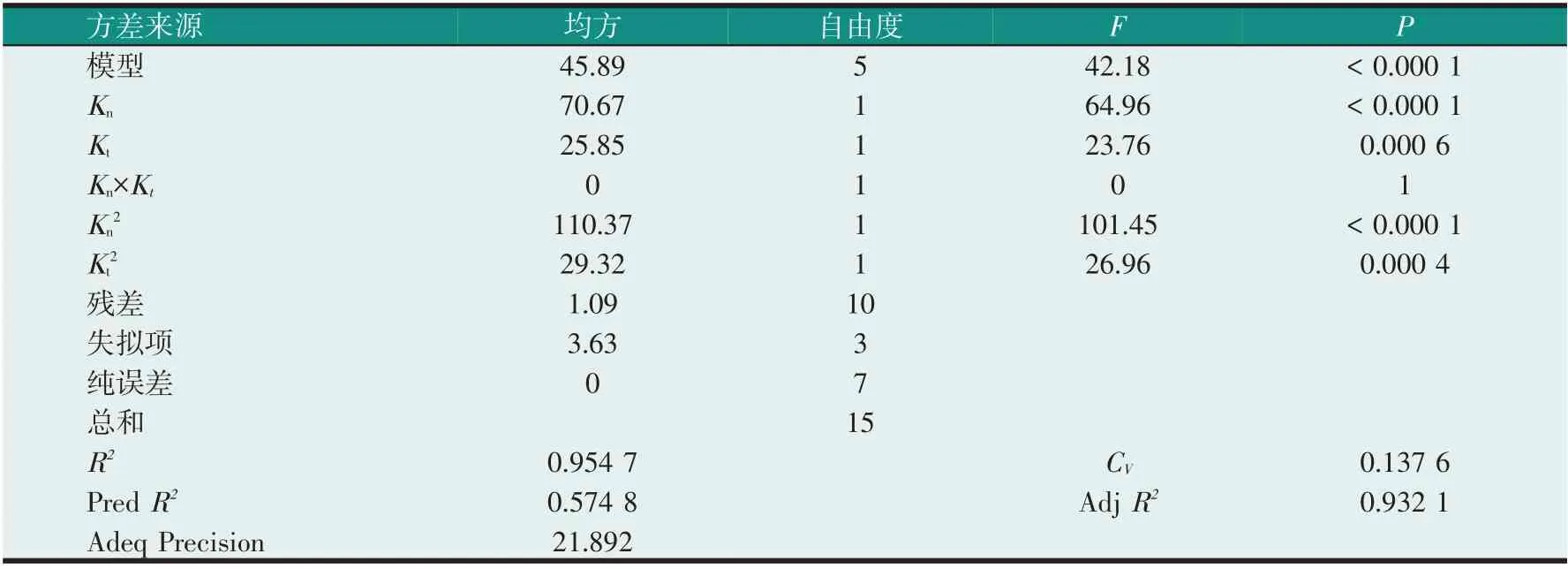
表7 粘结参数响应曲面试二次全模型方差分析

当δ取最小值2.41%时，得单位面积法向刚度（Kn）、单位面积剪切刚度（Kt）分别为4.11×1010、7.13×109N/m3。此时计算的Kn、Kt即为标定值。

2.5 结果验证

为验证标定粘结参数的可行性和准确性，以标定后的粘结参数为基础建立离散元仿真模型，并进行挤压、剪切台架试验（每组试验重复20 次，取均值），得到仿真试验与台架试验的临界破碎力及其相对误差，如表8 所示。结果表明，破坏力误差均在5%以内，且挤压和剪切仿真试验中均存在良好的线性阶段，建立的模型和标定的参数能够真实模拟颗粒饲料的破碎。

表8 破坏力误差分析（N）

3 破碎过程分析

根据图5、图6可知，力的作用速度对颗粒饲料的破碎无影响，破碎过程主要与其受力方式有关（挤压、剪切）。开展挤压、剪切方式下的颗粒饲料破碎过程仿真，设置圆柱压头挤压速度为0.3 mm/s、切刀压头剪切速度为1.0 mm/s，两种受力方式下的颗粒破碎过程及Bonding 键的破坏数量分别如图8 所示。其中，Bonding键的破坏数量可在EDEM软件Analyst模块中分析获取。

颗粒在受挤压作用的过程中（见图8a、图8b），圆柱压头与饲料样品最初接触时，饲料样品因受压力开始收缩，发生微小的塑性变形，此时Bonding键破坏数量较少。随着圆柱压头进一步下降，饲料样品内部颗粒不断被挤压，Bonding键破坏数量显著增加，从侧面产生裂纹。随着不断地挤压，饲料样品从裂纹处开始产生断裂，并伴随着部分颗粒整体分离、散开，此时Bonding 键破坏数量达到峰值，表明颗粒在断裂的同时伴随着产生大量的颗粒破碎，造成饲料粉化，受破坏形成的颗粒断面较为粗糙。当饲料样品产生断裂后，圆柱压头对颗粒基本不产生破坏作用，Bonding键的破坏数量显著降低。

颗粒在受剪切作用的过程中（见图8c、图8d），随着切刀不断向下运动，与切刀接触的颗粒在剪切力的带动下与原来粘结一起的颗粒产生分离，Bonding 键的破坏数量显著增加，并伴随着少量的颗粒脱落，大量颗粒未出现明显的破碎，未产生粉化现象。

图8 颗粒饲料挤压、剪切破碎过程分析

综上所述，本研究的饲料样品承受剪切破坏的能力不及其承压能力（见图5、图6），但剪切破坏时不易产生粉化。由于饲料粉化会造成营养成分的流失，因此，在设计饲料加工、运输机械结构及调控其运行参数时，应尽量避免颗粒饲料遭受过大的挤压而产生粉化、破碎。

4 结论

①通过开展挤压、剪切、染色台架试验，对建立的颗粒饲料离散元模型粘结参数Cn、Ct进行了测试与计算，确定了临界法向刚度（Cn）为2.93×107Pa、临界剪切刚度（Ct）为2.22×106Pa。

②应用台架试验结合EDEM 仿真的方法，通过开展二次正交旋转组合试验，对颗粒饲料离散元模型粘结参数Kn、Kt进行了标定，确定了单位面积法向刚度Kn为4.11×1010N/m3、单位面积剪切刚度（Kt）为7.13×109N/m3。

③开展了颗粒饲料的挤压力、剪切台架试验与仿真试验对比，结果表明，台架试验与仿真试验测得的颗粒破坏临界力相对误差在5%以内，表明标定的参数准确可靠。

④颗粒饲料破碎过程分析表明，饲料样品承受剪切破坏的能力不及其承压能力，但剪切破坏时不易产生粉化。在设计饲料加工、运输机械结构及调控其运行参数时，应尽量避免颗粒饲料遭受过大的挤压而产生粉化、破碎。