注重关联和比较

贺艳

摘  要：

教学苏教版小学数学三年级下册《认识面积》一课，调整教学内容，引导学生关联并比较周长和面积，从而对面积建立正确的“第一印象”。具体包括：基于描述性定义、基于度量本质以及在数量关系视角下，比较周长和面积。

关键词：小学数学；面积；周长；比较

本文系江苏省教育科学“十四五”规划2021年度课题“小学数学教师单元整体教学能力提升的实践研究”（编号：JC/2021/16）、江苏省南京市中小学教学研究第十四期重点课题“指向深度理解的小学数学单元整体教学研究”（编号：2021NJJK14Z32）的阶段性研究成果。

一、教前思考

苏教版小学数学三年级下册第六单元《长方形和正方形的面积》，安排了两部分内容：一部分是“面积的概念、面积的比较和测量以及面积单位”，即例1—例3；另一部分是“长方形和正方形的面积计算以及面积单位之间的进率”，即例4—例7。根据以往的教学经验，如果按照教材编写的内容和顺序组织教学，学生学完新课后，遇到面积、周长的综合题（如第二部分后的练习九和整个单元后的复习题中的一些习题）时，常常会将面积和周长混淆，具体表现在面积和周长的判断、面积单位和长度单位的使用、面积计算方法和周长计算方法的使用等方面，典型错误如图1所示。

究其原因，从内容的角度看，周长和面积都是平面图形的属性，前者是封闭图形周围边线的长度，后者是封闭图形内部区域的大小；对于同一个平面图形而言，常常是“周内有面，面外有周”。因此，周长和面积是紧密联系的两个概念，学习时自然容易混淆。从教学的角度看，根据苏教版小学数学教材的安排，学生在三年级上册（第三单元《长方形和正方形》）学习周长的内容，在三年级下册学习面积的内容；而学习面积内容时，在新授课中基本不涉及周长内容（只在例3中类比长度单位引入面积单位，以及在例3后的“想想做做”第2题中要求比较1厘米和1平方厘米）。因此，周长和面积独立教学，缺少关联和比较，学生自然容易混淆。于是，我尝试在《认识面积》

一课（三年级下册第六单元第一课，新授课），调整教学内容，引导学生关联并比较周长和面积，从而对面积建立正确的“第一印象”，避免从一维的周长到二维的面积的负迁移。

二、教学过程

（一）基于描述性定义，比较周长和面积

根据教材例1，教师引导学生观察、触摸黑板面、数学书的封面、课桌面、数学本的封面、文具盒面、直尺面等，感受、比较它们的大小，从而基于感性认识——面有大小，得出面积的描述性定义：面的大小。

然后，教师播放两个视频——一个是用手摸凳子的一周，一个是用手摸凳子的表面（分别如图2、图3所示），引导学生比较：都是在用手摸凳子，有什么不同？学生回答：一个摸的是凳子一周的长度，是凳子的周长；一个摸的是凳子表面的大小，是凳子的面积。教师让学生再找一些物体，摸它的一周和表面，并说一说它的周长和面积分别在哪里。由此，让学生基于描述性定义，明确周长和面积的联系和区别：都是封闭图形的属性，一个表示周围边线的长度，另一个表示内部区域的大小。

（二）基于度量本质，比较周长和面积

根据教材例2，教师引导学生思考比较无法通过观察、触摸以及重叠比较大小的两个面大小的方法，从而引出数方格这一先度量（对统一的“面积单位”进行计数）后比较的方法，让学生认识到：作为面的固有属性，面积是（更小的、基本的）面的积累，不比较大小时，也是可以度量多少的。

然后，教师出示圖4，让学生说出其中图形的周长和面积。学生通过数线段和数方格的方法得到：周长为16，面积为12。教师追问：16个什么？12个什么？也就是说，它们的单位分别是什么？学生交流得到：16个小方格边长，12个小方格面积。由此，引导学生基于度量本质，感悟周长和面积的联系和区别：周长和面积都可以通过度量得到，都表示度量单位的累加；周长是长度单位的累加，面积是面积单位的累加。

（三）在数量关系视角下，比较周长和面积

师  既然周长和面积紧密联系——对于同一个平面图形

来说，“周内有面，面外有周”，那么，它们之间会有怎样的数量关系？猜一猜：对于同一个平面图形来说，周长越大，面积越怎么样？面积越大，周长越怎么样？

生  我觉得，周长越大，面积越大；面积越大，周长也越大。

师  是这样吗？我们来验证一下。根据这个猜想，如果面积不变，那么，周长也应该不变。请同学们拿出方格纸，画出一个面积是12个小方格大小的图形，并求出它的周长。

（学生画图。）

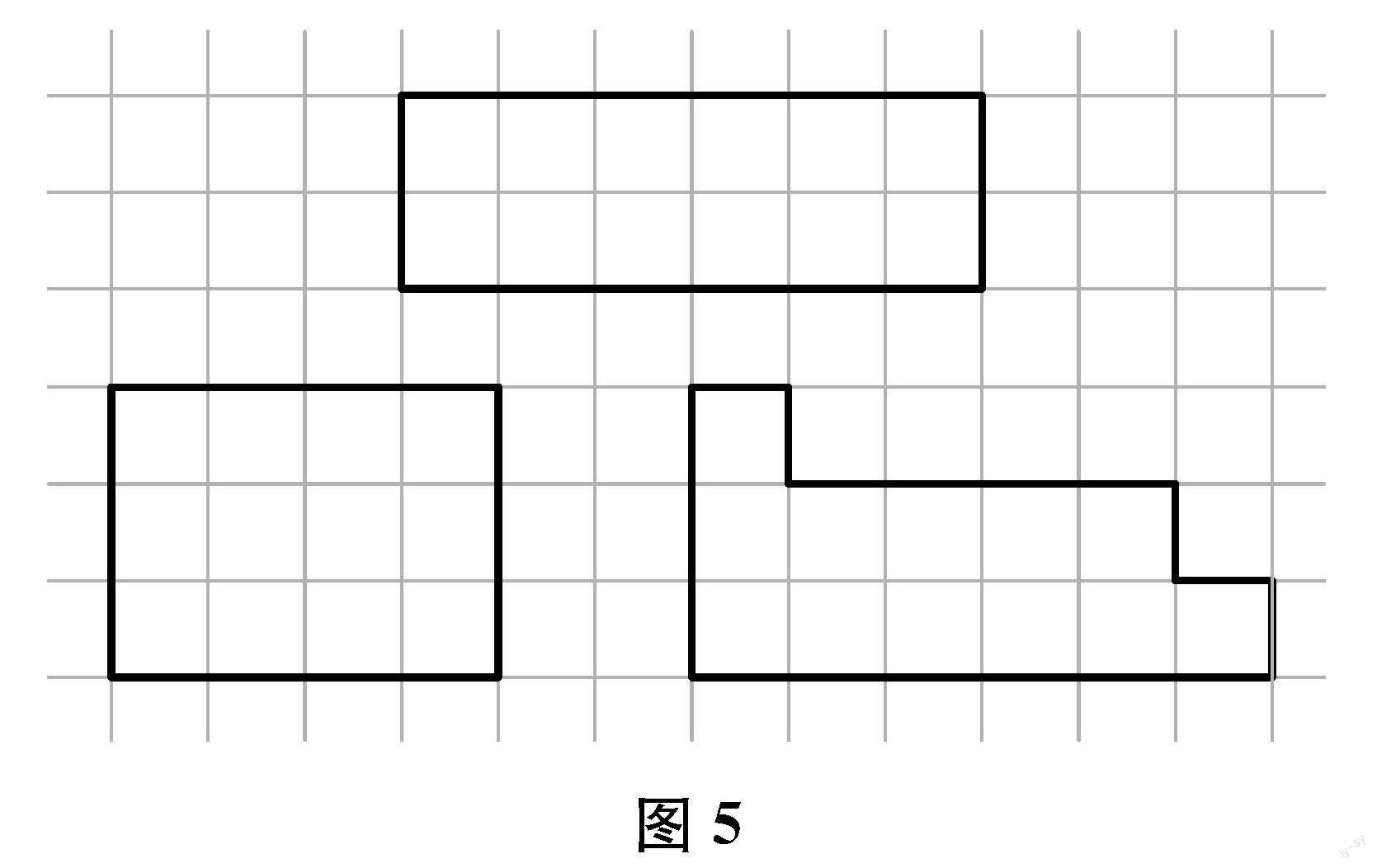
师  （展示学生作品，如图5所示）这三个图形的面积都是12个小方格大小吗？它们的周长相等吗？

生  三个图形的面积都是12个小方格大小，但是，它们的周长不相等，分别是16个小方格边长，14个小方格边长，18个小方格边长。

师  你有什么发现？

生  我发现，面积相等的图形，周长不一定相等。

师  换句话说，“周长越大，面积越大”并不成立。再来看周长不变时面积变不变。请同学们画出一个周长是20个小方格边长的图形，并求出它的面积。

（学生画图。）

师  （展示学生作品，如图6所示）这四个图形的周长都是20个小方格边长吗？它们的面积相等吗？

生  四个图形的周长都是20个小方格边长，但是，它们的面积不相等，分别是16个小方格大小，24个小方格大小，25个小方格大小，21个小方格大小。

师  你有什么发现？

生  我发现，“面积越大，周长越大”也不成立。

师  由此看来，周长和面积之间没有明确的数量关系。是不是与我们猜想的不一样？

生  我还发现，围成正方形的面积最大。

师  很有价值的发现！实际上，面积一定时，周长有最小的情况，没有最大的情况；周长一定时，面积有最大的情况，没有

最小的情况。这是数学中很重要的结论。随着数学学习的不断深入，同学们会逐渐深刻地认识这个结论。

在前两个角度的比较下，学生能认识到周长和面积是紧密联系的两个概念。本环节考察周长和面积的数量关系，引导学生发现：面积不变时周长可变，周长不变时面积也可变。从而在进一步的比较中，对周长和面积的概念有了深刻理解，同时体会到“变与不变”（控制变量）的数学思想（科学方法）。