14Cr9Mo1.5Co1.2NbNB转子钢材料 蠕变疲劳寿命预测研究

黄亮 艾迪 田宇 马新博 王丽艳

(哈尔滨汽轮机厂有限责任公司，黑龙江 哈尔滨 150046)

蠕变疲劳交互作用的本质是蠕变损伤和疲劳损伤的相互关系。疲劳的主要损伤形式是裂纹在晶内扩展，蠕变的主要损伤形式是空洞在晶界形核和长大。当蠕变和疲劳损伤依次和同时发生时，一种损伤对另一种损伤的发展过程将产生一定的影响，从而加速或减缓总损伤，进而影响疲劳寿命，即为蠕变疲劳交互作用[1]。

汽轮机转子在高温高压条件下工作，汽轮机组在频繁启停过程中，会伴随着温度的升高或降低，温度分布不均匀引起的热应力变化，使汽轮机转子不仅产生蠕变损伤，还会产生疲劳损伤，且蠕变损伤及疲劳损伤往往会发生交互作用[2-4]。当局部的蠕变疲劳载荷高于材料的疲劳极限时，材料会发生塑性变形，从而萌生裂纹，进一步降低转子在服役工况下的使用寿命，导致材料提前失效。因此，采用不同的方法对转子钢材料进行疲劳蠕变寿命预测具有重要的工程实际意义[5]。

目前，已有相关研究人员提出了不同的蠕变疲劳寿命预测模型。COFFIN提出了频率分离法，但由于未考虑压缩保载可能产生的拉伸平均应力，以及对裂纹产生的焊合作用，因此预测精度不高[6-7]；MANSON提出了应变范围划分法，具有较高的预测精度，得到了广泛的应用，但不适用于寿命非常短或保载时间过长的情况[6,8]；何晋瑞在应变范围划分法的基础上提出了应变能划分法，该模型具有较高的预测精度，但试验量较大，且该理论没有对微裂纹萌生之前的裂纹“扩展”“张开”做出解释[6,9]。

对于工程构件其运行工况是极其复杂的，在实验室条件下模拟蠕变疲劳时一般采用以下几种波形：第一种波形为无保持时间的对称循环疲劳即连续疲劳，也可根据需要采用非对称循环，即快拉伸-慢压缩或慢拉伸-快压缩；第二种波形为拉伸保持蠕变疲劳；第三种波形为压缩保持蠕变疲劳；第四种波形为对称保持蠕变疲劳[9]。且蠕变疲劳交互作用会受循环的应变幅(或应力幅)、应变速率(或频率)、保持时间、波形和环境等因素的影响[1]。

表1 14Cr9Mo1.5Co1.2NbNB钢的化学成分分析结果(质量分数，%)

本文对14Cr9Mo1.5Co1.2NbNB转子钢材料在620℃下进行了以下两种试验：(1)加载波形采用三角波，进行不同应变的低周疲劳试验；(2)加载波形采用梯形波，进行不同应变、不同保载时间的蠕变疲劳试验。并采用经验法及应变幅分割法两种寿命预测方法对14Cr9Mo1.5Co1.2Nb NB转子钢材料进行蠕变疲劳交互作用寿命预测，为转子的安全运行提供理论支持。

1 试验材料及方法

1.1 试验材料

以14Cr9Mo1.5Co1.2NbNB为试验材料，该材料用于超超临界机组高中压转子，通常在620℃下使用，其化学成分如表1所示。

1.2 试验方案

高温低周疲劳试验：试验设备采用MTS810-10t电液伺服疲劳试验机，如图1所示；试验温度为620℃；应变速率为0.002 s-1；应变分别为0.0035、0.0045、0.0055；应变比为-1；加载方式为三角波；将三个热电偶分别用细铁丝绑在上面卡具靠近试样的位置、试样中部及下面卡具靠近试样的位置，通过上、中、下三个热电偶测量试样标距段内的温度。

图1 MTS810-10t电液伺服疲劳试验机

高温蠕变疲劳试验：试验设备采用MTS810-10t电液伺服疲劳试验机；试验温度为620℃；应变分别为0.0035、0.0045、0.0055；应变比为-1；保载时间分别为10 min、20 min、30 min；加载方式为梯形波；将三个热电偶分别用细铁丝绑在上面卡具靠近试样的位置、试样中部及下面卡具靠近试样的位置，通过上、中、下三个热电偶测量试样标距段内的温度。

某科技公司的销售人员Jack照常8点半出门坐地铁去上班，地铁站距离公司还有3公里左右的路程，Jack用手机扫开一辆共享单车，骑行到公司。下午，要外出见客户，Jack约了一辆滴滴顺风车。司机师傅很能聊，一路上跟Jack聊得很愉快。见完客户已是晚上7点，手机显示电量不足，Jack来到一个Shopping Mall扫开了一个共享移动电源。走出Shopping Mall，下雨了，Jack再次拿出手机，扫开了一把共享雨伞……

装好引伸计，关好炉门，仔细检查引伸计的陶瓷棒不与矩形孔的任何一边接触。用石英棉把炉子的上下缝隙塞严，以减少散热，提高加热和保温的效率。试验采用温度控制器控制炉温和升温速率，待炉温达到620℃并恒温保持30 min后，开始试验。

2 蠕变疲劳寿命预测模型介绍

对于服役于蠕变疲劳条件下的构件，蠕变疲劳寿命即服役寿命是至关重要的，是构件设计必需的基本数据，也是对服役一定时间的构件进行安全性评估的依据[9]。蠕变疲劳寿命受诸多因素的影响，包括应变幅、应变速率、频率、加载波形、保载时间等因素，因此很难找到适合各种条件下的统一模型[9]。本文采用经验法和应变幅分割法建立14Cr9Mo1.5Co1.2NbNB转子钢材料的蠕变疲劳寿命预测模型。

2.1 经验法

2.2 应变幅分割法

在一个应力-应变循环中会包含塑性应变和蠕变应变，也会包含拉应变和压应变，这些不同性质的应变会以不同的方式影响总损伤。线性累积损伤法只考虑总应变幅而未区分不同性质的应变，会产生较大的误差。应变幅分割法的目的是将应力应变循环按其变形性质分为若干分量，分别评价各分量引起的损伤。如图2所示，AC为拉伸塑性应变，CD为恒应力拉伸蠕变应变，DB为压缩塑性应变，BA为压缩蠕变应变[9,11]。

(1)塑性应变幅Δεpp：为可逆塑性应变，等于拉伸和压缩塑性应变中较小的一个。

(2)蠕变应变幅Δεcc：为可逆蠕变应变，等于拉伸和压缩蠕变应变中较小的一个。

(3)塑性-蠕变应变幅Δεpc：拉伸塑性应变被压缩塑性应变反向后还有剩余应变；压缩蠕变应变被拉伸蠕变反向后还有剩余应变，两个剩余应变相等。这个剩余应变代表拉伸塑性应变和压缩蠕变应变所构成的应变幅。

图2 典型的蠕变疲劳循环

(4)Δεcp：代表压缩塑性应变和拉伸蠕变应变所构成的应变幅。对于一个循环来说，Δεpc和Δεcp中只能有一个。即，总的非弹性应变幅等于各应变幅之和：

Δεt=Δεpp+Δεcc+Δεpc

Δεt=Δεpp+Δεcc+Δεcp

NΔεα=C

考虑各应变幅之间的交互作用，设总的非弹性应变幅为Δεt，各应变幅分数如下：

则综合寿命与各分寿命的关系为：

式中，Nf是各应变幅共同作用下的综合寿命。

应变幅分割法的最大优点是能够得到给定循环的不同类型应变引起的损伤值，尤其在没有任何特殊假定的情况下包含了压缩应变对寿命的影响[9]。此模型利用蠕变疲劳循环中各个非弹性应变分量来描述塑性、蠕变及塑性-蠕变交互作用对高温蠕变疲劳损伤的贡献，在蠕变作用明显的情况下具有良好的适用性[9]。

3 试验结果分析与讨论

3.1 低周疲劳试验

14Cr9Mo1.5Co1.2NbNB高温低周疲劳试验采用轴向应变控制，应变比为-1，使用伺服闭环控制系统对试验过程进行控制和数据采集。选取循环峰值拉伸应力下降到曾出现的最大循环峰值拉伸应力σmax的50%时的循环周次作为失效循环数Nf，以Nf/2作为循环稳定滞回周次。其试验结果如表2及图3所示。

表2 14Cr9Mo1.5Co1.2NbNB低周疲劳结果

图3 不同应变下的低周疲劳寿命和应变分量

3.2 蠕变疲劳试验

14Cr9Mo1.5Co1.2NbNB高温蠕变疲劳试验采用应变保持，加载方式为梯形波。选取循环峰值拉伸应力下降到曾出现的最大循环峰值拉伸应力σmax的20%时的循环周次作为失效循环数N。由低周疲劳试验数据可得出不同应变下的塑性应变幅，由蠕变疲劳试验数据可得出不同应变下的塑性-蠕变应变幅，其试验结果如表3及图4所示。

采用经验法及应变幅分割法两种方法建立14Cr9Mo1.5Co1.2NbNB转子钢材料620℃下的蠕变疲劳寿命预测模型。采用经验法得到的蠕变疲劳寿命计算值及误差见表4及图5，经拟合，其蠕变疲劳寿命预测公式为：

(lgNf)0.5=-3.79096-2.26234S+0.7387S2

+0.31845S3+1.1507×10-4

+0.51152H-0.2573H2

表3 14Cr9Mo1.5Co1.2NbNB蠕变疲劳结果

图4 不同应变保载时间下蠕变疲劳寿命、蠕变应变分量

表4 经验法蠕变疲劳寿命计算值及误差

图5 不同应变下蠕变疲劳寿命实测值与计算值比较

表5 应变幅分割法蠕变疲劳寿命计算值及误差

采用应变幅分割法得到的蠕变疲劳寿命计算值及误差见表5及图6，塑性应变幅Δεpp单独作用相当于不发生蠕变的低周疲劳，塑性应变幅与疲劳寿命之间满足下述关系[1]：

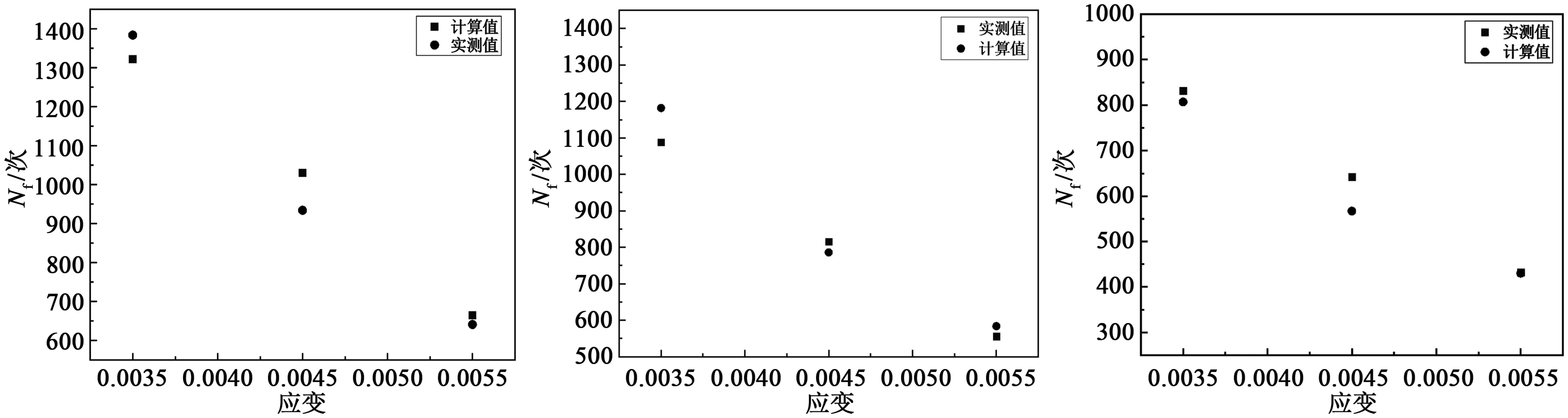
(a)保载10 min (b)保载20 min (c)保载时间30 min

NfΔεpα=C

根据表2低周疲劳试验结果，经拟合，其拟合结果为：

Npp0.99Δεpp=2.82

Ncp0.64Δεcp=0.10。

由表4及表5数据可以得出，试验寿命与预测寿命的相对误差均较小。证明了建立的寿命预估表达式能够较好地预测本次试验条件的失效寿命。

4 结论

采用经验法及应变幅分割法建立了14Cr9Mo1.5Co1.2NbNB转子钢620℃下的蠕变疲劳寿命预测模型，两种蠕变疲劳寿命预测模型均具有较高的精度，预测寿命与实际寿命的误差均较小，可为转子的安全运行提供理论支持。