天然气管网动态仿真三种隐式差分法对比研究

李春奇，袁献忠，李 俊，郭 乔

(1.中国石油化工股份有限公司天然气分公司，北京 100029； 2.国家管网集团川气东送天然气管道有限公司，湖北 武汉 430223； 3.西安石油大学 石油工程学院，陕西 西安 710065)

引 言

作为一种清洁、高效的化石能源，天然气的利用受到世界各国的重视，长距离管道运输无疑是最方便、经济的天然气运输方式。由于季节、天气、用户数量、突发事件等因素的影响，管道内的天然气流动一般是不稳定和瞬态的，对于愈加大型化的天然气管网，管道内的流动更加复杂。对流动参数的准确预测是保证天然气管道安全运行的前提。在这种情况下，管网仿真的作用就显得尤为重要[1]。

输气管道流动状态可由质量守恒方程、动量守恒方程和能量守恒方程描述，有多种方法可求解三大守恒方程。由于特征线法[2]、MacCormack[3]法均受制于稳定条件的约束，时间步长只能取得很小，如果仿真过程较长，则需要消耗较长的计算时间。而隐式差分法计算步长比较方便，能够选取较大的时间步长，减少计算次数和时间[4]。

对于隐式差分法，存在多种差分格式。国内众多学者[5-12]将不稳定流方程以有限差形式应用于位居四点网格中心的点子。Kiuchi[13]，Abbaspour和Chapman[14]，对时间项采用向前差分进行离散，对流项采用中心差分进行离散，并称这种差分格式为Implicit Cell Centered Method；郑建国[15]，王鹏[16-18]，向月[19-20]在Implicit Cell Centered Method的基础上，对偏微分方程组的非线性项进行泰勒展开，保留一阶项忽略高阶项。不同的差分格式直接影响管网仿真的计算精度，不同的差分格式适用于不同的求解方式，进而影响仿真计算速度，因此，寻找方程组合适的差分格式至关重要。

1 仿真理论

1.1 管道模型

管道模型用于描述管道内的流动状态，对于管道横截面积不发生变化的管道，可建立质量守恒方程、动量守恒方程和能量守恒方程[7]，并将其统一写为向量形式[16]

(1)

其中各参数见表1。

表1 管道数学模型相应变量的含义Tab.1 Meaning of variables in pipeline mathematical model

其中，p为流体压力，Pa；m为质量流量，kg/s；T为流体温度，K；Tg为环境温度，K；A为管道截面积，m2；ρ为流体密度，kg/m3；t为时间变量，s；θ为管段倾角，rad；w为流体流速，m/s；x为沿管道变量，m；g为重力加速度，m/s2；d为管道内径，m；D为管段外径，m；z为高程，m；cv为流体比热容，J/(kg·K)；K为总传热系数，W/(m2·K)；λ为摩阻系数，无因次，可由柯尔布鲁克公式计算，即

(2)

式中：Re为雷诺数，无因次。状态方程选择BWRS状态方程。

1.2 隐式差分法

为求解式进行离散化，使用不同的差分格式得到不同的离散方程，进而得到不同的计算结果，因此研究中心有限差分法、Implicit Cell Centered Method以及Implicit Cell Centered Method线性化法3种方法的差分格式以及相容性。

1.2.1 差分格式

将管道在空间上划分为N等分，每一等分长度Δx，在时间上每一时间步长为Δt，纵坐标表示时间，横坐标表示空间，如图1所示。

(1)方法1：中心有限差分法

中心有限差分法是将不稳定流方程以有限差形式应用于位居四点网格中心的点子，离散格式为

(3)

(4)

(5)

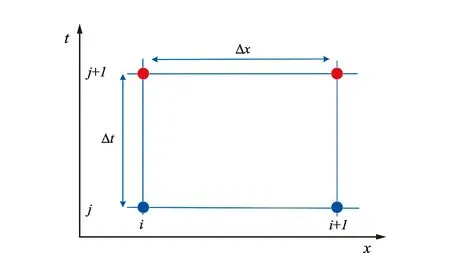
图1 隐式差分法网格图Fig.1 Grid diagram of implicit difference method

(2)方法2：Implicit Cell Centered Method

Implicit Cell Centered Method是对时间项采用向前差分进行离散，对流项采用中心差分进行离散，离散格式为

(6)

(7)

(8)

(3)方法3：Implicit Cell Centered线性化

Implicit Cell Centered线性化是在Implicit Cell Centered方法离散格式的基础上，对式中的B、F在上一时间层处进行泰勒展开，并忽略2阶无穷小项，具体格式为

(9)

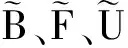
1.2.2 相容性分析

相容性意味着当时、空步长均趋近于零时，离散方程逼近微分方程，也就是说当时、空步长趋近于零时，如果离散方程的截断误差趋近于零，则称此离散方程与微分方程相容[21]。对于管道模型，3种不同方法的相容性如下：

定义微分算子：

(10)

对于方法1，定义差分算子

(11)

因此，方法1的截断误差为

(12)

同理，方法2的截断误差为

(13)

方法3的截断误差为

(14)

对于3种差分格式，当时、空步长趋近于零时，其对应的截断误差也趋近于零，因此3种格式都具有相容性。但是由于方法3采用了泰勒展开，这就导致该方法要求相邻时间层的B、F、U相差不能过大，否则将存在较大的截断误差。

1.3 方程组求解方法

将管道划分为n个管段后，针对每个管段建立质量守恒、动量守恒以及能量守恒方程，并联立边界条件，即可求解管道中每个节点的压力、流量和温度。一般而言，求解非线性方程组要比求解相同维度的线性方程组的计算速度慢，方法1和方法2所建立的方程组是非线性方程组，可以使用牛顿拉夫逊法求解，对于方法3则是将非线性项线性化后，可建立稀疏线性方程组，求解该稀疏线性方程组，因此方法3的计算速度较快。

2 结果对比

2.1 算例描述

为了对比仿真结果，分别以3种差分格式应用于同一个仿真案例。水平管道内径600 mm，管道长度为5 km，粗糙度为0.025 mm，标准状态：压力为101.325 kPa，温度为20 ℃。天然气组分见表2。

表2 天然气主要组分Tab.2 Main composition of natural gas

初始时刻管道处于稳定状态：进口压力为6 MPa，温度为30 ℃，流量为0 Nm3/h。零时刻以后，进口恒定压力6 MPa，在第6 s时刻出口流量变为3×105Nm3/h，保持到第18 s，并瞬变为0 Nm3/h，直至36 s仿真结束，如图2所示。

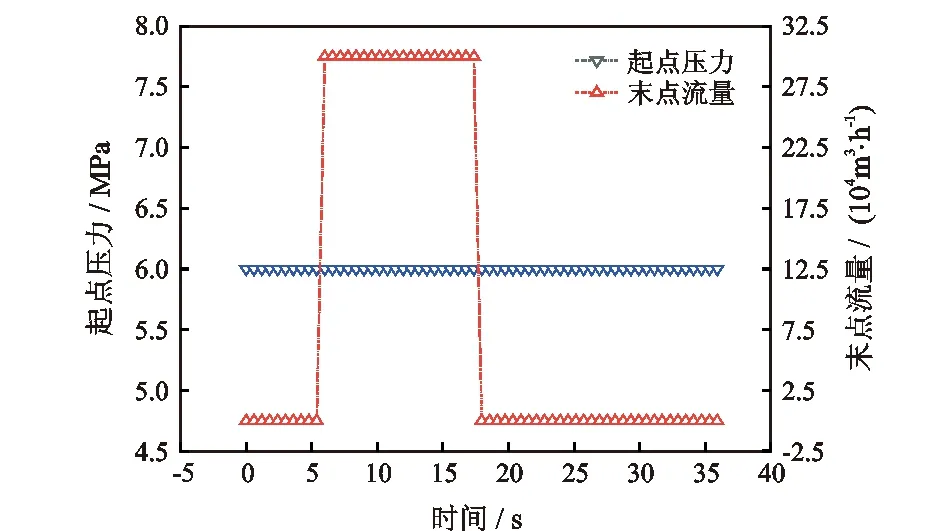
图2 边界条件Fig.2 Boundary conditions

2.2 计算精度

为了对比计算精度，分别以3种差分格式求解上述仿真案例，分别设置空间步长、时间步长为0.2 km、0.6 s，并且在相同的条件下与PNS油气管网仿真软件[22]计算结果对比，分析第12 s、24 s、30 s以及36 s时刻的流量、压力分布(图3)。

图3 不同时刻的流量、压力分布图Fig.3 Flow rate and pressure distribution at different times

从图3可以看出，在第12 s、24 s以及36 s时刻，方法2、方法3两种方法的流量分布以及压力分布基本重合，且与PNS仿真结果吻合度较高。而方法1计算的流量和压力分布与PNS计算结果存在较大偏差，并且无论在哪个时刻，方法1所计算的流量分布和压力分布均存在不符合客观规律的波动。

2.3 计算速度

在求解管道动态仿真时，以第i时层的水力热力参数作为初始值，求解第i+1时层的，而计算速度又与方程组初始值有关，为了避免初始值不同对求解速度的影响，因此只观察管道流动突变时刻时的单层计算速度，此时方程组的初始值均相同，即上一时层的计算结果。

不同的分段数意味着构建不同规模的方程组，分段数越大，方程组维数越多。为了对比不同分段数下的计算速度，分别对比将管道划分为5段、10段、20段和25段时的仿真耗时(图4)。

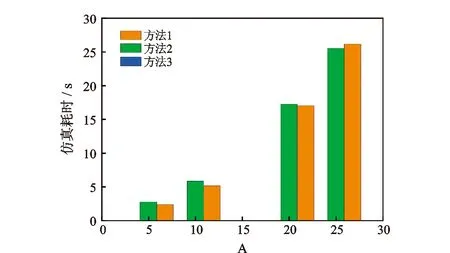
图4 3种方法仿真耗时Fig.4 Time consumption of three simulation methods

从图4中可以看出，无论在哪一时刻，方法3计算耗时基本为0，计算速度远高于另外两种，而方法2与方法1计算速度相差无几。这是由于方法1与方法2需要通过迭代求解非线性方程组，并在迭代的过程中，需要更新流体物性，这就导致每迭代一次的耗时不仅包含非线性方程组的求解耗时，也包括每次迭代时的流体物性更新耗时，仿真耗时较大；而方法3直接求解线性方程组，无需迭代也无需更新物性，故而计算速度较快。

3 结 论

(1)相容性：3种方法均具有相容性，即当时间步长和空间步长趋近于零时，离散截断误差也趋近于零。

(2)计算精度：中心差分法计算精确性较差，无法正确描述天然气管道的动态仿真过程，而Implicit Cell Centered和Implicit Cell Centered线性化法计算精度相当。

(3)计算速度：由于中心差分法与Implicit Cell Centered法计算速度较慢，而Implicit Cell Centered线性化法直接求解线性方程组，并且计算过程中不需要更新物性，计算速度非常快，故在后期的天然气管网动态仿真研究中推荐使用Implicit Cell Centered线性化法。