天然气管网反输工况下的运行优化

周 军，秦一雄，彭井宏，梁光川，赵云翔

(1.西南石油大学 石油与天然气工程学院，四川 成都 610500； 2.北京燃气集团(天津) 液化天然气有限公司，天津 300450)

引 言

天然气由于其燃烧的高效和清洁性，逐渐取代了煤炭、石油等传统化石能源。我国天然气供应长期以传统管道气(PNG)为主体，为缓解国内能源供应紧张问题，加快了液化天然气(LNG)进口终端建设，形成了多气源供应格局[1]。随着国家管网公司的成立，天然气市场“X+1+X”体系的形成，LNG因其供应输送的灵活性和高热值的特点，在国内的天然气市场中表现出强劲的竞争力。目前，我国下游用户需求气量持续上涨，而部分管网实现了下游LNG的管网反输功能，有效缓解了上游气源供气能力有限的状况，增加了管网供气方案的多样性。因此，在上游气源供气能力小于下游用户需求气量时，管道运营商如何合理选择各气源供应量，确定管道运行方案，提高管道运行效益显得十分迫切和重要。

关于天然气管网运行优化的相关问题，国内外学者已进行了大量研究[2-5]。针对该问题，通常通过构建包含目标函数、约束条件和决策变量的数学模型，并选用求解算法达到求解优化的目的。常见的优化目标为压缩机站能耗最小化[6-8]、气体输送量最大化[9]、经济效益最大化[10-11]等，构成单目标优化问题。多目标问题是指同时考虑多个优化目标，但这些目标之间相互矛盾，需通过优化手段实现管道整体运行状态最优[12-14]。在数学优化模型中，压缩机的运行作为关键的优化变量，压缩机的开关机及开机台数等变量会产生离散化问题、非线性规划问题[15]和混合整数非线性规划问题[16]。在求解算法方面，最早使用的是传统的优化算法[17-19]，后续出现随机优化算法[20-22]，以及商业求解器[23-25]。

本文选择以管道运行经济效益最大化为优化目标，以气源供气量、压缩机开机数和转速为决策变量建立相应的运行优化模型。该模型中还涉及节点压力、管道水力、压缩机运行等约束条件。在此基础之上，选择国内某管道为优化实例，利用GAMS建模系统和SBB求解器进行优化求解并对优化结果进行经济和技术分析。

1 数学模型

天然气长输管道系统是指将天然气从气田或处理厂运输到城市门站的管道，运行压力较高(一般在4～10 MPa之间)、管径较大(一般在500～1 000 mm之间)，典型天然气长输管道系统如图1所示。实际上，天然气输送系统远比图1中所示的结构复杂，天然气干线存在许多的分支，形成多种形式的复杂管网拓扑结构。

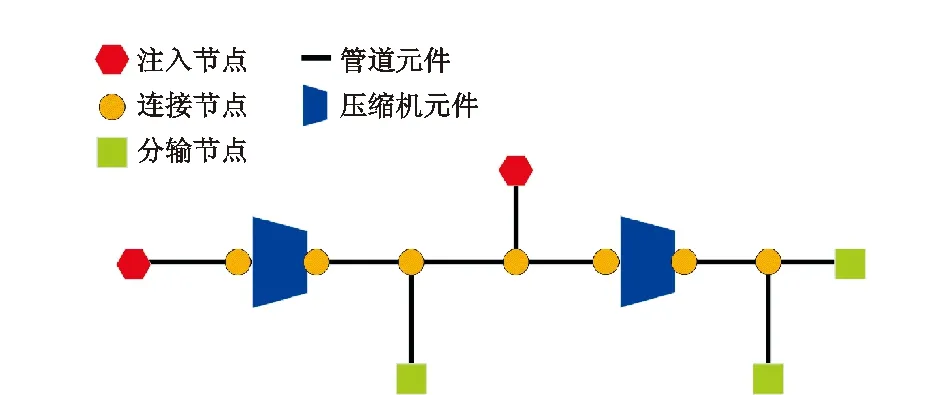
图1 典型天然气长输系统的结构Fig.1 Structure of typical long-distance natural gas transmission system

为了更好地建立管道优化数学模型，运用运筹学中有向图理论G=(N,U)来表示混合气源管网系统，其中N为节点i的集合，包括注入节点IN、连接节点TN和分输节点DN，所有i满足i∈N；U为元件e的集合，包括管道元件PL和压缩机站元件CS，所有e满足e∈U。

节点与集合间关系为

N=NIN∪NTN∪NDN。

(1)

式中：NIN为注入节点集合；NTN为连接节点集合；NDN为分输节点集合。

元件与集合间关系为

U=UPL∪UCS。

(2)

式中：UPL为管道元件集合，集合中元素用k表示；UCS为压缩机站元件集合，集合中元素用j表示。

基于以上理论，建立天然气管道运行优化模型[26]。

1.1 系统假设

多气源协同供应的天然气管网的运行优化问题十分复杂。在实际情况中，天然气在管网中流动时，气体的水力参数和热力参数等会随时间变化而变化，处于一种不稳定状态(瞬态)。但通常我们研究的是管道日运行规划问题，时间较短，且长输管线中气体温度会达到等于或接近环境温度的恒定值，因此使用稳态工况近似分析瞬态问题。

1.2 目标函数

随着LNG相关产业的发展，以及未来天然气消费量的不断增长，多气源的供应使得管网供气方案有了新的选择，而如何在满足下游用户需求气量的前提下，实现管道运行经济效益最大化一直是管道运营商关注的主要问题，管道运行经济效益主要由售气收益减去系统成本得到，系统成本又包括购气成本和压缩机运行成本。管道运行经济效益最大化目函数

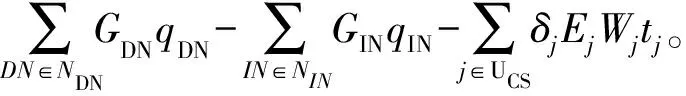
(3)

式中：GDN为分输点处天然气销售价格，元/m3；qDN为分输点处天然气需求气量，m3/d；GIN为注入节点处天然气购买价格，元/m3；qIN为注入节点处天然气供应气量，m3/d；δj为压缩机站的压缩机开机数；Ej为压缩机站能耗价格，元/(kW·h)；Wj为压缩机站单机功率，kW·h；tj为压缩机单日运行时间，h。

1.3 管道模型

(1)管道水力计算公式

由于管道内壁粗糙，天然气在管道内流动时会产生一定的摩阻损失，造成天然气能量损失，导致压力随管线下降。水平输气管道水力计算公式

(4)

(5)

式中：qk为标准状况下天然气的体积流量，m3/s；C为常数，C=0.038 4；Psp,k为管道首端压力，MPa；Pep,k为管道末端压力，MPa；Dk为管道内径，m；λk为沿程损失系数；Zk为天然气压缩因子；Δ为天然气相对密度；Tk为天然气平均温度，K；Lk为该管段长度，m；Ra为空气的气体常数，Ra=287.1 m2/(s2·K)；P0为标准状况压力，P0=1.013 25×105Pa；T0为标准状况温度，T0=293.15 K。

(2)沿程损失系数计算

沿程损失系数(水力摩阻系数)主要作用在运动方程中，与天然气流态和管道的粗糙程度等因素有关，是影响管道沿程压降的主要因素，进而影响仿真结果的准确性。管道摩阻系数计算公式有Weymouth、Colebrook、Pan(A)、Pan(B)等，可根据管径和流态范围选择不同的公式。其中，最常用的就是Colebrook公式，该方程适用于紊流的3个区域，且计算精确度高，如下所示：

(6)

(7)

式中：εk为输气管道内壁相对粗糙度，mm；λk为水力摩阻系数；Rek为雷诺数；ρo为标准状况下空气的密度，ρo=1.206 kg/m3；μ为天然气动力黏度，N·s/m2。

(3)压缩因子计算

压缩因子是一个无量纲量，表明了真实气体与理想气体之间的差异，是进行管道水力计算时必须考虑的一个校正因子。压缩因子Z随着气体组成、所处的压力与温度的不同而改变，通常运用经验公式进行计算。BWRS方程是基于大量试验数据得到的状态方程，其精确度在所有经验公式中最高，计算公式为[27]

(8)

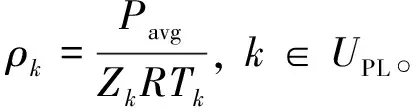
(9)

式中：Zk为管道天然气压缩因子；R为天然气的气体常数，R=428.5 m2/(s2·K)；A0、B0、C0、D0、E0、a、b、c、d、α、γ为状态方程的11个参数；ρk为天然气密度，kg/m3。

1.4 压缩机站模型

天然气管网中压缩机的布置方式会根据实际需求的不同而设置，压缩机串联可增加排气压力，并联可增加排气流量。对于长输管网，由于管输流量较大，压气站内多采用并联方式布置压缩机。

(1)压缩机特性方程

在压缩机运行过程中，当流量过低时，将出现喘振现象；而流量过高，又将出现滞止现象，两种现象都将影响压缩机的工作性能，因此，压缩机的处理流量需满足设计的工作区间约束，如图2所示。由图2可知，离心压缩机的工作区间约束由压头特性曲线组成。离心式压缩机的效率特性曲线如图3所示。

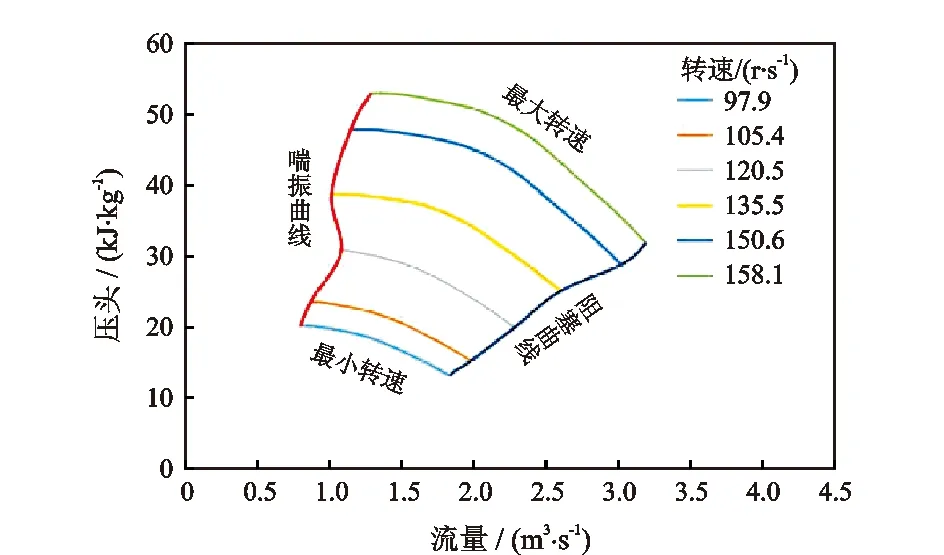
图2 压缩机工作区间示意图Fig.2 Schematic diagram of compressor working interval

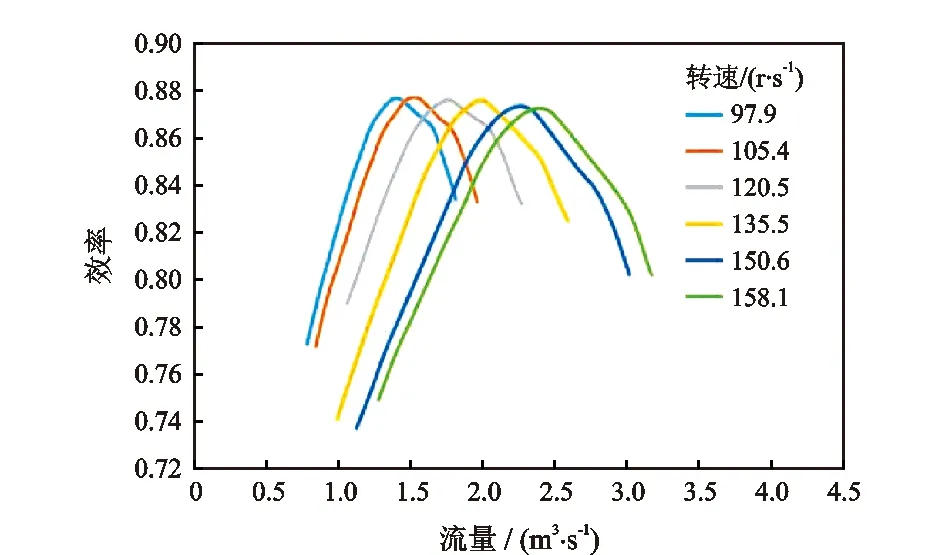
图3 压缩机效率特性曲线Fig.3 Characteristic curves of compressor efficiency

在压缩机优化建模的过程中，压缩机的特性曲线并不能直接使用，需要将其拟合成特性方程。方程以流量和转速为变量，根据非线性最小二乘法回归确定压缩机特性曲线拟合的方程系数A、B、C、D。

离心压缩机压头

j∈UCS。

(10)

离心压缩机效率

j∈UCS。

(11)

式中：ηj为压缩机效率；A2、B2、C2、D2为由特性曲线拟合的效率系数。

喘振最小流量约束方程为

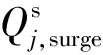
滞止最大流量约束方程为

(13)

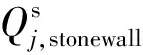
压缩机的排气压力可根据式(10)计算，即

(2)压缩机能耗计算

压缩机指示功率是指直接用于对天然气进行压缩增压的功率，即

(15)

式中：Nj为指示功率，kW；Mj为气体质量流量，kg/s。

压缩机轴功率是指驱动设备传递到压缩机主轴上的功率，在传输过程中会由于机械损失消耗一定的功率，即机械效率，此外还需要辅助功率进行修正，因此

(16)

式中：Nj，s为压缩机轴功率，kW；ηj，m为机械效率；Nj，A为辅助功率，kW。

电动机的使用具有清洁高效、动力提供稳定等特点，离心压缩机驱动设备多选用电动机，耗电量

(17)

式中：Wj为耗电量，kW·h；tj为驱动时间，h；Nj，t为压缩机总功率，kW；ηj，e为驱动效率。

1.5 约束条件

(1)节点流量平衡约束

根据质量守恒定律，在任意节点处，流入节点的流量之和应与流出节点的流量之和相等：

(18)

式中：qi为节点流量，m3/d，当天然气从节点流入管网系统，取值为正，当天然气从节点流出管网系统，取值为负；βie为与第i个节点与第e个元件之间的连接关系系数，βie=0代表第i个节点与第e个元件不相连接，βie=1代表天然气从第e个元件流入第i个节点，βie=-1代表天然气从第i个节点流出到第e个元件；qe为元件流量，m3/d。

(2)注入节点流量约束

注入节点处天然气的供应量受到产地的产量影响，具有最大产量和最大处理能力约束，注入节点流量应满足最大流量约束：

0≤qIN≤qIN,max。

(19)

式中：qIN，max为注入节点最大供气量，m3/d。

(3)分输节点流量约束

天然气输送的主要目的是满足不同区域和不同用户的用气需求，因此，在各分输节点处流量应达到节点用户最小需求气量

qDN,min≤qDN。

(20)

式中：qDN，min为分输节点最小需求气量，m3/d。

(4)分输节点压力约束

通常末端天然气用户在接收天然气后，会再输送至其他用户，因此，在各末端分输节点处压力应满足节点用户最低需求压力

PDN,min≤PDN。

(21)

式中：qDN,min为分输节点最低需求压力，MPa。

(5)管道压力约束

为防止高压天然气在管道内流动时，对管道内壁产生较大的应力，造成管道变形，从而影响天然气的安全输送，规定管输运行压力不可超过管输的最大允许运行压力：

Pk≤Pk,max。

(22)

式中：Pk为管道运行压力，MPa；Pk,max为管道最大允许运行压力，MPa。

(6)压缩机约束

压缩机的压比一般约为1.2～1.4，增压能力有限，为满足下游压力需求，需要规定压缩机的最小进气压力：

ps,min≤ps。

(23)

式中：ps，min为压缩机允许的最小进气压力，MPa。

同时，为保证天然气安全输送，压缩机的出口压力不可超过最大排气压力：

pd≤pd,max

(24)

式中：pd，max为压缩机允许的最大排气压力，MPa。

在压缩机的运行过程中，根据管网实际运行情况，调度人员会通过调节压缩机转速来控制压缩机的运行情况。由离心压缩机工作区间可知，压缩机的转速存在一定的限制范围，压缩机最大、最小转速约束

nj,min≤nj≤nj,max。

(25)

式中：nj，min为压缩机最小转速，r/s；nj，max为压缩机最大转速，r/s。同时，压缩机的处理流量也存在一定的界限，超出界限将会产生喘振和阻塞等现象，因此压缩机的流量约束应满足

qj,surge≤qj≤qj,stonewall。

(26)

式中：qj,surge为压缩机最小进气流量，m3/s；qj,stonewall为压缩机最大进气流量，m3/s。

压缩机站内的单台压缩机设备存在最大和最小轴功率约束

Wj,min≤Wj≤Wj,max。

(27)

式中：Wj,min为压缩机最小功率，kW；Wj,max为压缩机最大功率，kW。

1.6 决策变量

根据目标函数及约束条件建立的数学模型中，优化变量为注入节点处天然气供应气量qIN、各压缩机站开机台数δj和转速nj。其中，注入节点处天然气供应气量和压缩机转速为连续性变量，压缩机开机台数为离散变量。同时具有线性约束条件和非线性约束条件，构成了一个混合整数非线性规划问题(MINLP)，具有一定的求解难度。

2 求解方法

针对本优化问题，选择通用数学建模系统GAMS(General Algebraic Modeling System)软件进行编程求解。本文建立的MINLP模型在GAMS中可由DICOPT求解器和SBB求解器求解。DICOPT求解器基于等式松弛策略外部逼近算法的扩展，SBB求解器基于混合整数线性规划标准的分支定界(B&B)法和一些GAMS支持的标准NLP求解器的组合。对于含有重要和困难组合部分的模型，DICOPT可以更好地执行，而对有较少的离散变量的模型，除了更困难的非线性外，SBB可更好地求解[28]。本文模型中的离散变量仅由压缩机的开机方案产生，离散变量较少，所以调用SBB求解器对模型进行求解。

本文使用GAMS 24.8.2 进行编程，计算机配置为Intel(R) Core(TM) i5-4200H CPU 2.80 GHz的处理器和16 GB 的运行内存(RAM)。

3 算例研究

本文选择国内某管道作为研究算例。目前，该管道已实现末站反输，供气方式从仅由陆上气田供气转为海陆双气源保供，末站设计年反输规模为25.2×108m3。现阶段该管道全长2 229 km，含有1条干线、1条专线、4条支线，管道结构示意图如图4所示。在没有反输任务时，具有2个注入节点IN1和IN2，7座压气站和28个分输节点；在进行反输任务时，应先满足末端分输节点DN28需求气量再进行反输，因此，具有3个注入节点IN1、IN2和IN3，8座压气站和27个分输节点。管道设计运行压力10 MPa，干线管道内径995 mm，管道壁厚21 mm，管道内壁绝对摩阻系数0.01 mm。

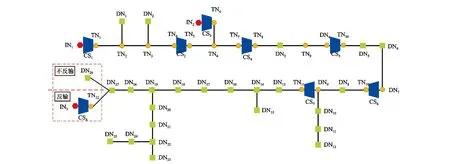
图4 管道示意图Fig.4 Schematicdiagram of pipeline system

过去5年注入节点IN1和IN2的日供气量变化如图5所示。由图5可知，注入节点IN1为该管道的主要注入节点，第1年开始，节点IN1供气量约为2.0107m3，随着注入节点IN2的引入，IN1供气量略有下降，并通过注入节点IN2的供气量互补，从第4年开始IN1供气量波动减小，供气量仍小幅度持续升高，最终日供气量维持在(2.3～2.5)107m3。第1年初，注入节点IN2开始供气，并在第3年初趋于稳定，日供气量维持在(1.4～1.6)107m3。第5年注入节点IN1和IN2日供气总量约为(3.7～4.1)107m3。根据重庆石油天然气交易中心提供的管道天然气成交单价和上海石油天然气交易中心提供的LNG出厂价格指数，确定各注入节点购气价格，见表1。

过去5年每日下游总需求气量如图6所示。由图6可知，下游总需求气量逐年递增，第5年每日下游总需求气量较第1年增长60%，使用Origin 2021b软件对下游总需求气量进行线性拟合，并通过拟合结果对未来5年的需求气量进行预测，如图7所示。

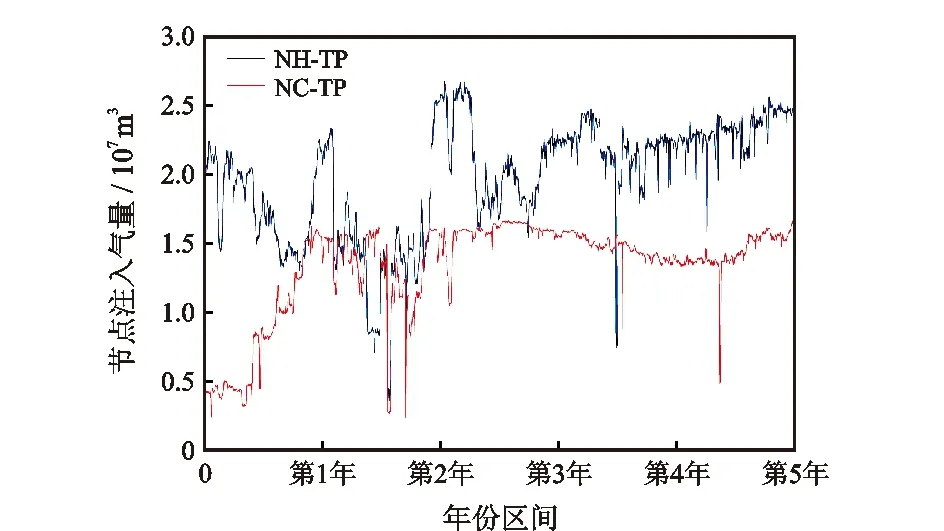
图5 不同时期各注入节点日供气量Fig.5 Daily gas supply of each injection node in different periods

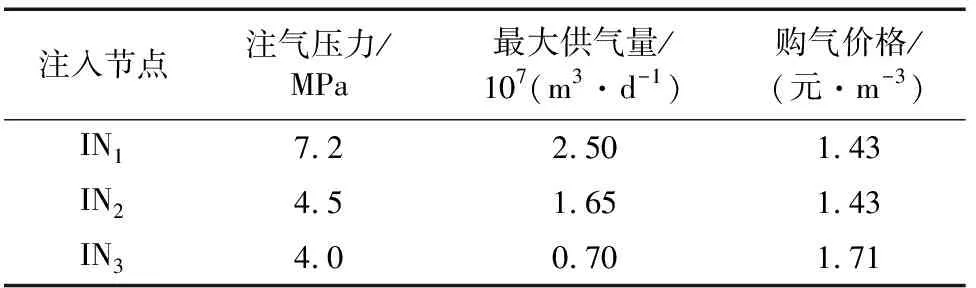
表1 各注入节点供气边界及购气价格Tab.1 Gas supply boundary and gas purchase price of each injection node

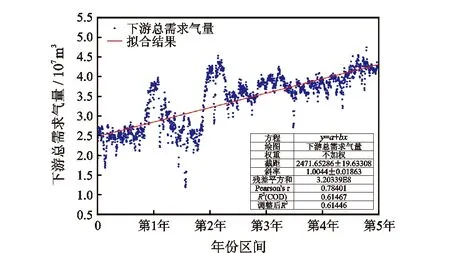
图6 不同时期每日下游总需求气量Fig.6 Total daily gas demand ofcustomer in different periods

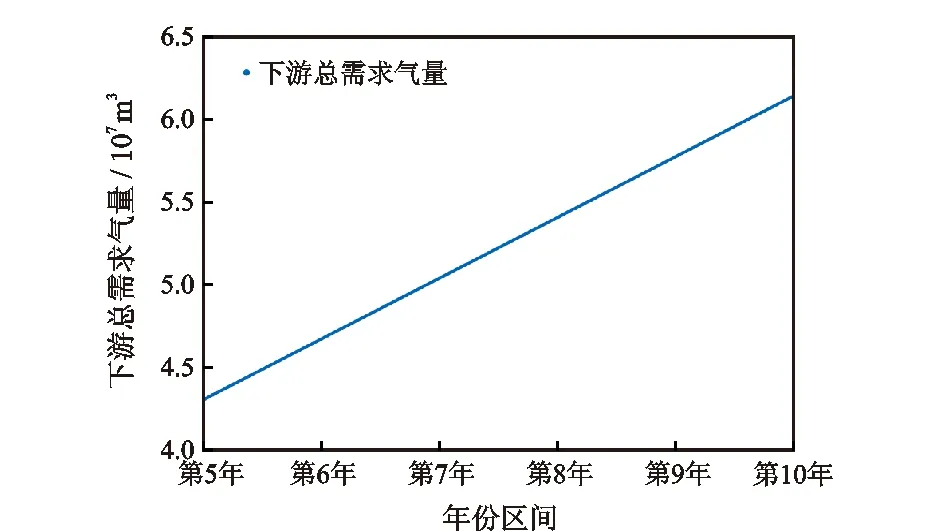
图7 未来5年不同时期每日下游总需求气量Fig.7 Total daily demand of customer in different periods over the next 5 years

以该管道第4年某日的实际运行工况和第6年某日预测工况为例展开研究。第4年当日管道总输量为4.072 4×107m3/d，第6年当日管道总输量为4.854 6×107m3/d，反输时先满足分输节点DN28需求气量，并根据反输设计规模，注入节点IN3具有0.7×107m3/d的反输能力。在第6年时，上游气源供气能力不变，供气压力不变。根据《关于调整天然气基准门站价格的通知(发改价格〔2019〕562号)》，确定各分输节点天然气基准门站价，管道中各分输节点处的流量分配情况及售气单价如图8所示。由图8可知，下游分输节点较多，大部分分输节点需求流量较小，维持在0.2×107m3/d左右，其中需求流量超过0.4×107m3/d的分输节点共有4处，分别为DN2、DN15、DN21和DN27。要求下游末端节点压力不低于4 MPa。

图8 各分输节点需求流量及售气单价Fig.8 Gas flow-rate demand and unit price at each distribution node

干线各压缩机站内均配置相同型号的离心式压缩机，并采用2用1备的形式并联布置。在8座压气站中，所有压缩机均由电动机驱动，单台压缩机最大功率分别为7 200 kW、11 000 kW和15 000 kW 3个等级，各压缩机配置参数见表2。由于各压缩机站建设投产时间不同，因此具有的增压能力不同，各压缩机的特性也不同。此外，根据管网运行公司在2020年发布的产品运行报告计算压缩机运行费用系数为0.56 元/(kW·h)。同时，要求各压缩机的进气压力不低于3 MPa。

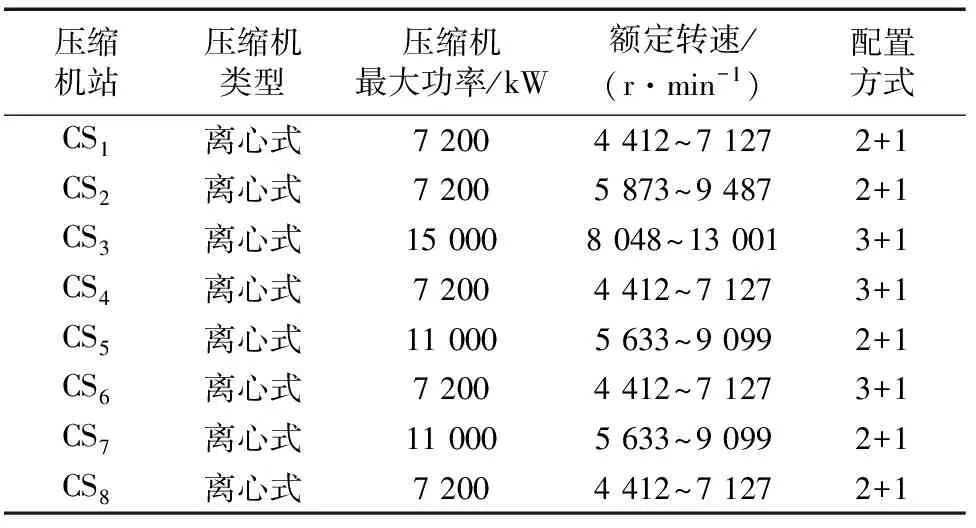
表2 各压缩机站配置参数Tab.2 Configuration parameters for each compressor station

4 结果和讨论

为了确定注入节点供气量、压缩机开机数和压缩机转速对管道运行效益的影响，本文选择了4种管道运行方案进行优化，并对优化结果进行分析和讨论。方案一为注入节点IN3反输至分输节点DN27的管道运行方案；方案二为注入节点IN1和IN2以最大供气能力输送的情况下，注入节点IN3反输至分输节点DN27的管道运行方案；方案三为注入节点IN3反输至分输节点DN26的管道运行方案；方案四为现场管道运行方案。不同反输方案和现场方案的费用对比情况见表3。由表3可知，影响管道运营商获得的经济效益的主要因素是售气利润。在需求增长的情况下方案二的运行经济效益最高，方案三的运行经济效益最低，二者相差16.5万元，对比两种管道运行方案可知，虽然方案三能耗费用较低，但对管道运行经济效益影响较小，较低的售气利润会带来较低的运行经济效益。方案一和方案二均反输至分输节点DN27，但方案二中注入节点IN1和IN2的供气量较多，由于燃气生产成本影响，管道气购气价格低于LNG购气价格，所以方案二的售气利润高于方案一，致使方案二的运行交易较高，所以在满足下游用户需求的条件下，选择管道气仍会带来较大的运行经济效益。结合方案一和方案二对比方案三可知，注入节点IN3反输的位置越远，管道能耗费用越低，但这也需要较多的反输气量，购气成本增加，售气利润降低。结合方案一、方案二和方案三对比方案四可知，下游需求气量的增长会带来更多的售气利润，但也增加了压缩机的处理气量。总体来说，进行管网反输会降低管道能耗费用，增加运行经济效益。

表3 不同管道运行方案下各注入节点供气量及运行费用对比Tab.3 Comparison of gas supply of each injection node and operation cost under different pipeline operation schemes

不同运行方案下的压缩机开机方案见表4，各压缩机站内压缩机转速如图9所示。结合表4和图9可知，各运行方案均主要在输气管道干线后端进行增压，下游各压缩机站增压量较为均匀，压缩机转速普遍维持在6 000 r/min左右，但这也产生了一定的增压能耗费用。在压缩机站CS2处，由于注入节点IN2注气压力较低且供气量大，所以压缩机转速较高，会产生较高的能耗费用。

表4 不同管道运行方案下的压缩机开机方案Tab.4 Compressor startup schemes under different pipeline operating schemes

图9 各压缩机站内压缩机转速Fig.9 Compressor speed in each compressor station

不同运行方案下管道干线压降如图10所示。由图10可知，基于不同管道运行方案中注入节点的供气量变化，管道增压方式会发生改变。方案一和方案三中注入节点IN1和IN3的供气量波动较小，相差48.2104m3/d，所以产生的增压方式基本相同。方案二在压缩机站CS3处进行了增压，这是因为该方案在注入节点IN1处采用了气源最大供气量，在气源处增压会产生较高的能耗费用。方案三在压缩机站CS3后的干线增压方式与方案一和方案二相同。方案一、二和三在压缩机站CS7处增压至7.5～7.7 MPa，在CS8处的出口压力均为5.2 MPa，说明模型优化求解结果良好。方案四为满足末端节点压力要求，全线压力较高，产生了较高的管道能耗费用。

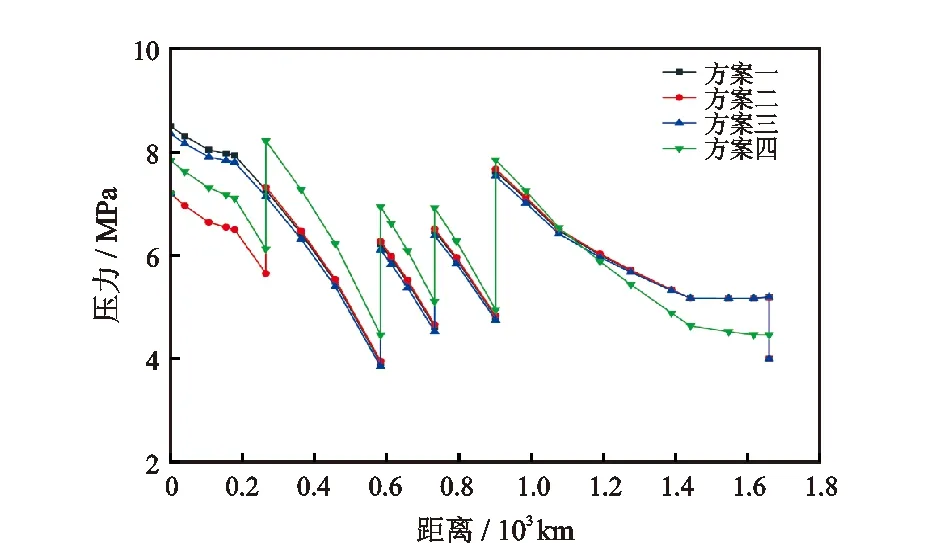
图10 不同运行方案下管道干线压降Fig.10 Pressure drop of main pipeline under different operation schemes

5 结 论

(1)在下游需求气量增长，上游供气压力不变，供气量达到上限时，进行管网反输会有效缓解供气紧张问题，且产生的管道运行能耗费用比常规输送更低；

(2)在进行管网反输时，反输气量越多，管道运行能耗费用越低，但售气利润也会随之降低，最终导致管道运营商获得的经济效益降低；

(3)在上游气源供气量充足时，常规输送带给管道运营商的经济效益仍比进行管网反输时高，管网反输仅适应上游气源供气能力不足时的情况。因为管道气的价格低于LNG的价格，且管道运行经济效益主要受售气利润影响。