成品油管道分输计划优化的并行模拟退火算法
陈海宏 ,左丽丽,吴长春,李清平
1 中国石油大学(北京)油气管道输送安全国家工程实验室/城市油气输配技术北京市重点实验室,北京 102249
2 中海油研究总院深水工程国家重点实验室,北京 100028
成品油管道运行与管理的重要内容之一是制定批次计划。可行的批次计划需满足站场分输/注入流量、站场分输/注入条件、管段运行流量、批量和批次次序等约束[1]。对于中石油现有成品油管道,借助于批次计划模拟软件,计划编制人员手工制定一个月的管道批次计划通常需耗时半天以上。为提高计划编制人员的工作效率,许多研究人员提出了批次计划优化模型与算法,并开发了相应的优化软件[2-9],明显缩短了计划编制时间。针对成品油管道批次计划优化问题,文献[10~13]采用离散时间方程建立了混合整数线性规划(MILP)模型,而文献[14~19]采用连续时间方程建立了批次计划优化的MILP模型。与离散模型相比,连续模型的规模更小,计算时间更短,优化结果质量更高[20-22]。当问题规模较小时,通过CPLEX商业优化软件一般可在较短时间内获取MILP模型最优解。随着问题规模的扩大,CPLEX软件的计算时间将大幅增加,其往往只能获取MILP模型较优解,有时甚至无法获取可行解,故CPLEX不适合于管道规模大、计划周期长、批次数目多、油品种类多的情况。为保证在较短时间内产生较优解,文献[11]提出采用模拟退火(SA)算法优化单点注入、多点分输成品油管道分输计划。然而,对于大规模问题,SA算法应用效果依旧不佳。为改善SA算法的优化效果,实现SA算法并行计算,本文提出构造分输计划新方案的两阶段法,并改进了目标函数。
以单点注入、多点分输成品油管道为研究对象,已知管道沿线各站场里程、各管段内径、各分输站分输流量上/下限值、各管段运行流量上/下限值、计划期内管道起点输入各批次的时间与流量、计划期开始时刻管道内各批次的油品种类、体积与位置、计划期内各中间分输站每种油品的分输需求体积,在满足管道运行约束的前提下,优化管道沿线各中间站分输计划,包括站场分输各批次的开始时刻、结束时刻、流量与体积。
1 并行模拟退火算法
1.1 算法总体框架
成品油管道分输计划优化的并行SA算法逻辑框架(图1)主要包含8个要素:目标函数、初始解构造方法、新解构造方法、新解接收准则、初始温度Tmax、终了温度Tmin、降温速率r、Markov链长度S。
(1)分输计划初始方案构造方法采用空间递推法(Space Recursive Method, SRM)[11]。按照SRM法,从上游站场至下游站场,依次基于经验规则编制各分输站分输计划初始方案。
(2)分输计划新方案构造过程分为两个阶段:第一阶段利用变量邻域解构造方法局部调整分输计划原方案;第二阶段基于分输作业衔接性规则微调第一阶段产生的分输计划新方案。
(3)在每次迭代过程中,同时分别构造多个新的分输计划,并选择一个最好的新解作为本次迭代的最终解,从而实现SA算法并行计算。若同时存在多个最好的新解,则从中随机选择一个。
(4)分输计划新方案接收准则为Metropolis准则:若新解优于旧解,则接收新解;否则,按概率接收新解。概率计算公式为:

其中,prof为差解被接收的概率;fn为新解目标函数值;fo为旧解目标函数值;T为SA算法的当前温度。
1.2 目标函数
以计划期内管道沿线所有管段运行流量波动幅度之和最小作为目标函数。

其中,JS为站场总数;KS为时间节点总数;g1为计划期内各管段运行流量总体波动幅度之和,m3/h;g2为计划期内各管段运行流量瞬时波动幅度之和,m3/h;cpj为管段j权重系数,用于避免运行流量的波动集中在某些管径较大、里程较长的管段上,建议取值为管段j体积容量与管道总体积容量的比值;csj,k为0、1变量,csj,k=1 表示时段(tk-1,tk)和(tk,tk+1)内管段j运行流量不相等,csj,k=0则表示运行流量相等;QDj,k为时段(tk,tk+1)内管段j运行流量,m3/h;QAj表示计划期内管段j运行流量的平均值,m3/h。计划期划分方法:选取计划期内管道沿线各站场执行分输/注入作业的开始时刻与结束时刻作为时间节点,将计划期划分为若干时段。
1.3 分输计划初始方案构造方法
为降低成品油管道分输计划优化问题的求解难度,假设计划期内任一中间站对同一批次至多执行一次分输作业。实际上,目前中石油成品油管道分输计划的编制基本上符合该假设。基于该假设,采用SRM法[11]构造分输计划初始方案。按照SRM法,从上游站场至下游站场,依次基于经验规则构造管道沿线各分输站分输计划初始方案。确定某站场是否分输某批次的原则:计划期内该批次可以到达该站场、该站场对该批次所含油品存在分输需求。确定某站场分输各批次体积的原则:按计划期内批次过站体积的比例将该站场分输每种油品的需求体积分配至各个批次。确定某站场分输某批次流量的原则:优先选取分输流量允许范围内的中间值。确定站场分输某批次时间的原则:为保证初始方案有较大的调整空间,将每次分输作业安排在批次过站时间窗的中间时段。
1.4 分输计划新方案构造方法
分输计划新方案构造过程(图2)可分为两个阶段。第一阶段为采用变量邻域解构造方法调整分输计划原方案;第二阶段为基于分输作业衔接性规则微调第一阶段产生的分输计划新方案。
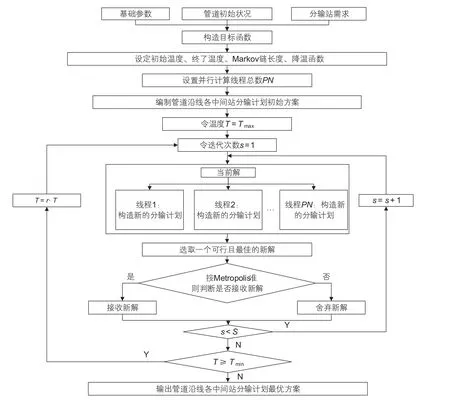
图1 成品油管道分输计划优化的并行SA算法示意图Fig. 1 Schematic diagram for optimizing delivery schedules of a multiproduct pipeline by parallel SA algorithm
(1)基于变量邻域解构造方法调整分输计划原方案
A 随机选择一个中间分输站sj。
B 随机选择一个批次si,其油品类型为sp。
C 若计划期内被选中站场未分输被选中批次,则增加一个新的分输作业;否则,从分输时间、分输流量、分输体积3个变量中随机选择一个变量,利用变量邻域解构造公式调整被选中分输作业的执行计划。变量邻域解构造公式[23]如下:
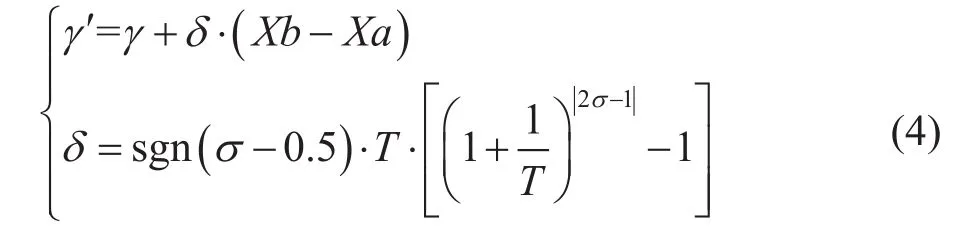
其中,γ为决策变量,Xa≤γ≤Xb;γ’表示γ的邻域解;T表示SA算法的当前温度;σ为0~1随机数;sgn为符号函数。
(2)基于分输作业衔接性规则微调分输计划
为提高分输计划新方案的质量,第一阶段基于变量邻域解构造法调整被选中分输作业后,尝试将该分输作业与其它中间站执行的分输作业进行衔接。若第一阶段调整的分输作业或者新增分输作业的执行开始/结束时刻与相邻某站场所执行分输作业的开始/结束时刻的时间间隔小于φ小时,则衔接这两个分输作业。φ一般可取5 h。

图2 分输计划新方案构造流程Fig. 2 Flowchart for generating a new delivery schedule
1.5 参数设置
根据SA算法理论可知,算法迭代总次数由外循环与内循环共同控制。初始温度、终止温度与降温函数可用于控制外循环执行次数,Markov链长度可用于控制内循环执行次数。根据文献[11]中SA算法参数设置方法进行参数设置,具体如下:
初始温度:Tmax= 1000 ℃。
终止温度:Tmin= 1 ℃。
Markov链长度:S =1000。
降温函数:T’=r×T。其中,r表示降温速率,0<r<1。需根据具体测试情况,综合比较优化结果的质量与计算耗时确定r最佳取值。
并行线程数PN:需根据具体测试情况,综合比较优化结果的质量与计算耗时确定PN最佳取值。
2 算例分析
以某成品油管道PA为例,验证并行SA算法优化管道分输计划的有效性。管道PA总长2000 km、内径544.8 mm、沿线共建有8个站场(编号分别为E0~E7);管道沿线各管段运行流量允许范围为400~1200 m3/h,沿线各中间分输站分输流量范围见表1。管道PA测试的计划周期为0~670 h,已知计划期内管道起点输入计划(表2)、计划期内管道沿线各中间站每种油品分输需求体积(表3)和初始时刻(0 h)管道内各批次的油品种类、体积及位置(表4),利用并行SA算法优化管道PA分输计划。
2.1 冷却系数r的影响
影响SA算法稳定性的最主要因素是冷却系数r。一般来说,r越大,SA算法优化结果质量越高,优化耗时越长,算法稳定性也越高。根据具体管道测试情况,综合优化结果质量与耗时可确定r推荐值。不考虑并行计算,设定不同的r值,应用SA算法优化管道PA分输计划(图3)。当0.05≤r≤0.85时,随着r增加,优化结果质量呈明显上升趋势。当0.85≤r≤0.95时,随着r增加,优化结果质量提升幅度较小,但计算耗时显著增加。因此,将r推荐值设定为0.85。

表1 管道PA沿线中间分输站分输流量允许范围Table 1 Delivering flow rate limits of intermediate stations along pipeline PA
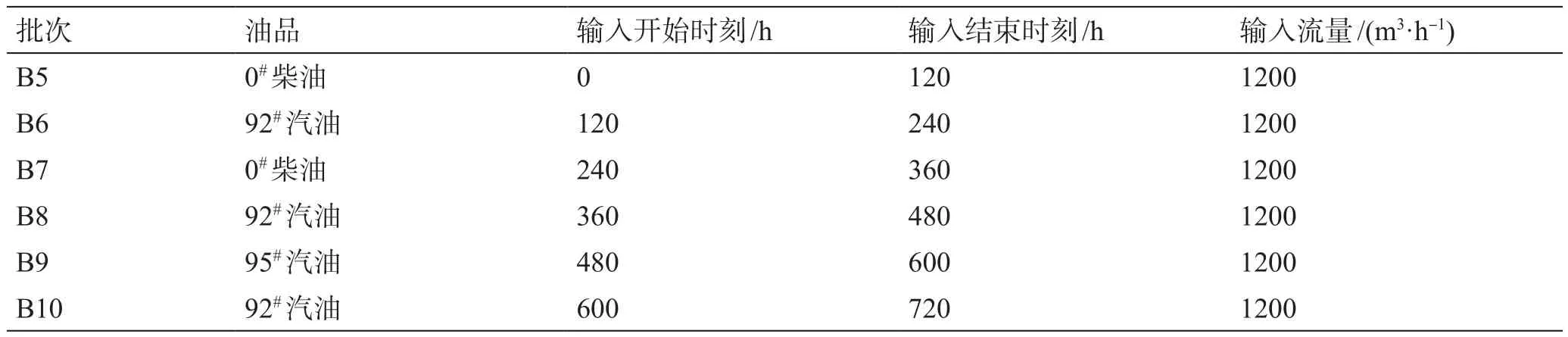
表2 计划期内管道PA起点输入计划Table 2 Inputting schedules for the initial station of pipeline PA during the scheduling horizon
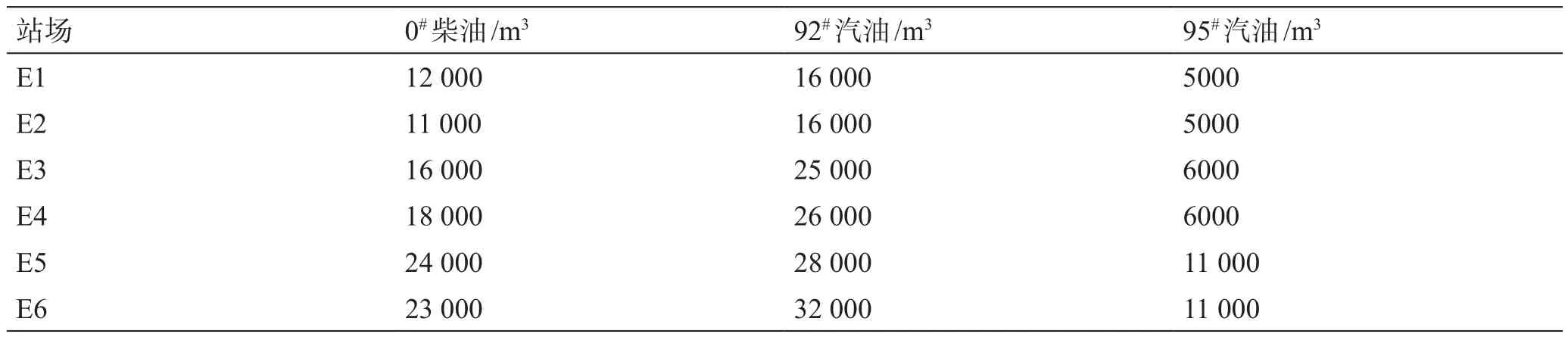
表3 计划期内管道PA中间分输站对各油品的分输需求体积Table 3 Product demands of intermediate stations along pipeline PA during the scheduling horizon

表4 初始时刻管道PA内各批次油品的种类、体积及位置Table 4 Product type, volume and location of every batch in pipeline PA at the initial moment
2.2 并行线程数PN的影响
令r=0.85,设定不同的并行线程数目PN,应用并行SA算法优化管道PA的分输计划(图4)。
(1)当1≤PN≤8时,随着PN增加,并行SA算法计算耗时呈线性增长。并行SA算法采用的并行策略为:每次迭代时,同时产生若干个新解,并选择质量最高的解作为本次迭代的最终解。总迭代次数不变,但每次迭代时由于增加了各线程之间的等待耗时,使得并行SA算法的计算耗时随PN增加而增大。当PN=8时,计算时间约为6 min,满足单条管道分输计划编制工作允许计算时间的要求。
(2)当1≤PN≤6时,随着PN增加,优化结果质量呈明显上升趋势,目标函数值由5010 m3/h降低至4490 m3/h。当6≤PN≤8时,随着PN增加,优化结果质量提升幅度较小,目标函数值由4490 m3/h降低至4480 m3/h,但计算耗时却由325 s增加至386 s,增长约19%。
综合考虑优化结果质量与计算耗时,将PN推荐值设定为6。与PN=1相比,当PN=6时,优化结果目标函数值降低约10%。
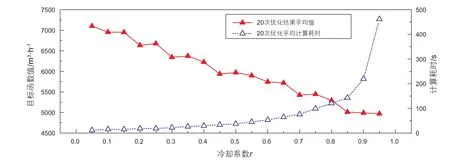
图3 不同冷却系数下,SA算法优化管道PA分输计划的结果Fig. 3 The optimization results for pipeline PA provided by SA algorithm with different cooling factors
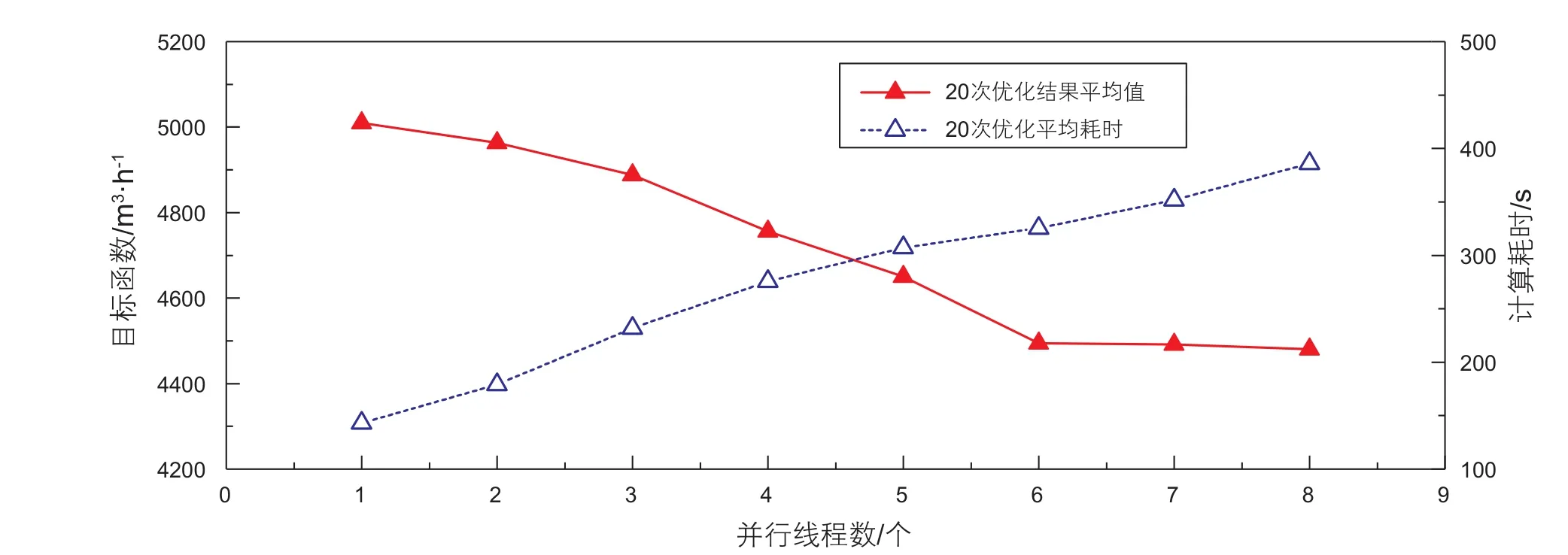
图4 当r=0.85时,不同并行线程数下,并行SA算法优化管道PA分输计划的结果Fig. 4 The optimization results for pipeline PA provided by parallel SA algorithm with different parallel threads when r=0.85
2.3 优化结果展示
令r=0.85、PN=6,20次应用并行SA算法优化管道PA分输计划,平均耗时约5.4 min,优化结果目标函数平均值为4490 m3/h。图5为某次利用并行SA算法产生的管道PA分输计划,优化结果目标函数值为4386 m3/h。图5中P1、P2、P3分别表示0#柴油、92#汽油、95#汽油。计划期内,中间分输站E1—E2、E3—E4、E5—E6之间所执行的分输计划具有很好的衔接性,保证了管道沿线各管段流量运行平稳。
2.4 并行SA算法与CPLEX对比
文献[10]采用离散时间方程建立了成品油管道分输计划优化的MILP模型,并利用CPLEX求解模型。基于文献[10]建立的MILP模型,利用CPLEX优化管道PA的分输计划。实际生产中,单条管道分输计划编制工作允许的计算时间一般不超过10 min。将计算时间设定为10 min,CPLEX成功产生了管道PA的分输计划,优化结果目标函数值为6021 m3/h。CPLEX与并行SA算法的计算过程如图6所示。与CPLEX相比,并行SA算法优化结果的目标函数值降低约27%,计算耗时降低约46%。从优化结果来看,并行SA算法明显优于CPLEX。
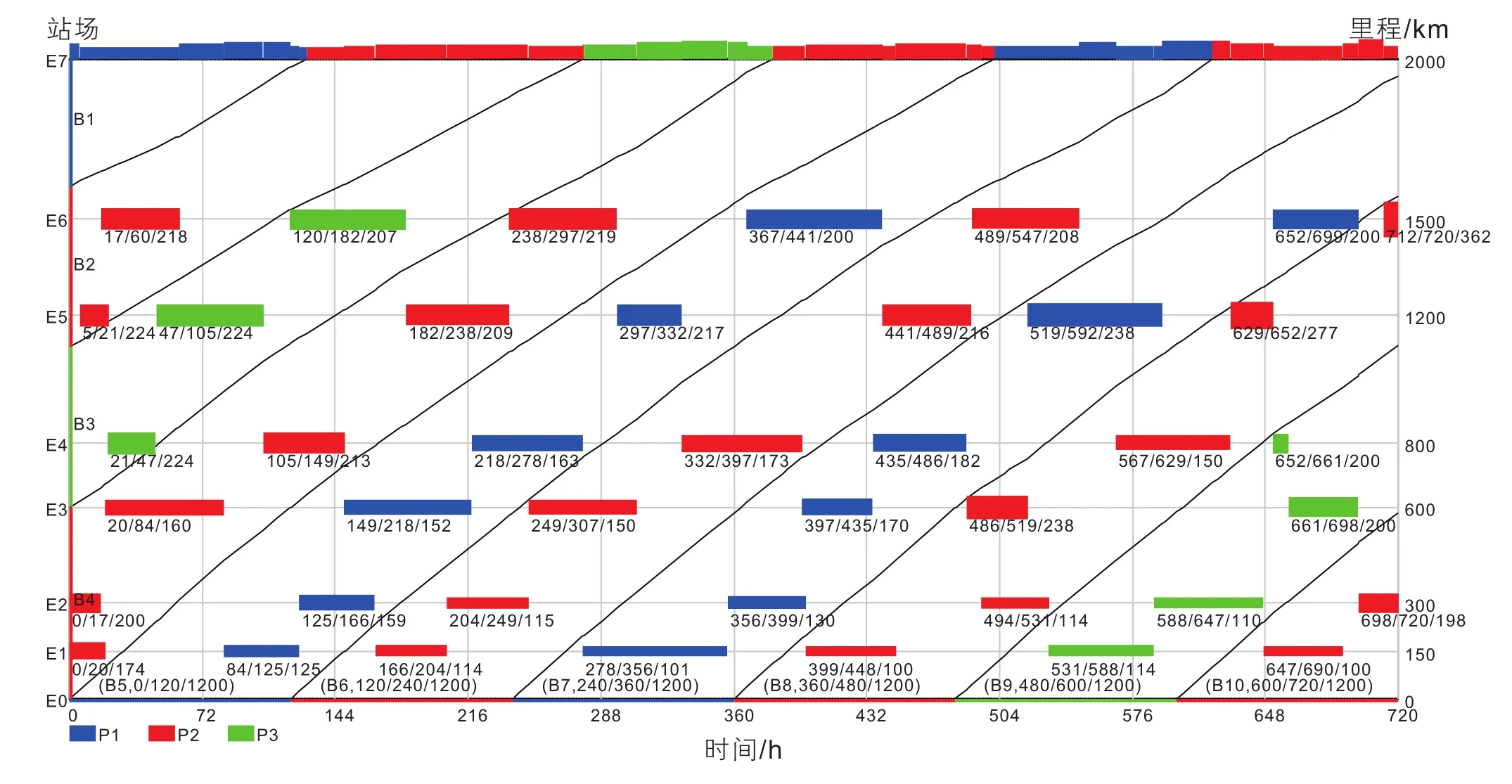
图5 当r=0.85、PN=6时,应用并行SA算法产生的管道PA分输计划Fig. 5 The delivery schedules of pipeline PA provided by parallel SA algorithm, when r=0.85 and PN=6

图6 CPLEX、并行SA算法优化管道PA分输计划的迭代过程Fig. 6 Computational processes about optimizing delivery schedules of pipeline PA using CPLEX and parallel SA algorithm
3 结束语
通过在SA算法中引入并行计算,建立了适用于成品油管道中间站分输计划优化的并行SA算法,其综合性能不仅优于非并行SA算法,而且优于CPLEX商业优化求解器。不同于非并行SA算法,并行SA算法最大的特点是:从当前迭代点出发同时构造并检验多个邻域解,选择其中最好者作为本次迭代产生的新迭代点。对于某成品油管道PA,将并行计算线程数取为6个,并行SA算法可以保证在计划编制工作可接受的计算时间内(不超过10 min)产生较优的成品油管道分输计划。基于并行SA算法产生的管道PA分输计划具有很好的衔接性,符合计划编制人员编制批次计划的要求,保证了管道沿线各管段流量运行平稳。与非并行SA算法相比,并行SA算法的优化结果目标函数值降低约10%。与CPLEX优化求解器相比,在10 min的计算时间内,并行SA算法的优化结果的目标函数值降低约27%。

