基于双约束的流体和岩性因子的叠前直接提取方法
马琦琦,孙赞东
中国石油大学(北京)地球物理学院,北京 102249
0 引言
地震波数据中蕴含了丰富的有助于揭示地下岩层及其孔隙流体特征的信息。随着勘探难度的加大以及勘探技术的进步,基于地震资料的地下岩性探测以及孔隙流体识别已成为现阶段油气勘探的关键技术[1]。在高品质的地震数据基础上,储层、流体识别的精度主要依赖于选取的弹性参数对于岩性和流体的敏感度以及提取弹性参数方法的可靠性[2-4]。
国内外学者利用弹性参数对储集层识别及流体检测方面做了大量的研究。Gregory和Domenico[5-6]提出了利用纵横波速度比VpVs识别流体;Fatti等[7]利用泥岩基线进行了烃类流体的检测;Goodway等[8-9]阐述了拉梅参数λ、μ和密度ρ的组合(例如,λµ、λρ、μρ)可以有效地识别储层和流体;Russell等[10]结合了孔隙弹性理论提出了Russell流体因子用来识别流体;印兴耀等[11]对基于Russell流体因子F和纵波阻抗Ip的两项弹性阻抗反演进行了研究;Du等[12]指出Russell流体因子可以有效识别烃类流体。
叠前数据相对于叠后数据,包含更多的地下介质信息[13]。叠前AVA/AVO(振幅随入射角度/偏移距变化)反演技术是提取隐藏在叠前地震数据中的岩性、流体信息的重要途径[14-15]。许多学者基于纵波反射地震数据进行了叠前反演的研究,然而纵波反射系数对横波信息和密度是不够敏感的[16]。因此,由于拥有更丰富的弹性信息,基于纵波和横波信息的叠前联合反演相对仅采用纵波数据的叠前纵波反演,可以获得更加优质的反演结果[17-19]。Stewart[20]首先提出了叠前联合反演方法,并利用纵、横波数据提取了纵波速度反射系数 ΔVpVp和横波速度反射系数 ΔVsVs;Buland和Omre[21]利用马尔科夫链的方法实现了联合反演;Viere和Landro[22]提出利用最小二乘估计算法求解PP和PS反射系数的近似线性表达式;Rabben等[23]利用Metropolis-Hastings算法实现了联合反演;张广智等[24]推导了基于脆性因子、泊松比和密度的近似方程,并利用联合反演提取了以上弹性参数;Lu等[25]采用泰勒展开和均值漂移法提高了叠前联合反演结果的准确性;杜炳毅等[26]推导了基于Gassmann流体项、剪切模量和密度的转换波公式,实现了基于这三个参数的联合反演;王彦飞等[16]提出了基于粒子滤波提供先验信息的L1范数约束的算法来进行联合反演,进一步提高了反演的精度。
在前人研究的基础上,本文提出了基于双约束的流体因子F、岩性因子μρ和密度ρ的联合反演方法。首先推导了基于F、μρ和ρ的纵波和转换波反射系数方程,并参考致密砂岩储层建立正演参数模型对新推导的公式进行精度分析,为实现F、μρ的直接提取奠定了基础,弹性参数的直接提取可以有效避免间接计算引入的累积误差。在实践中,由于地震资料质量不高、子波提取不准等问题,反演本身是一个不适定的问题,虽然PP-PS联合反演在一定程度上降低了解的不适定性,但是仍有必要在目标函数中增加适当的正则化约束来提高反演的稳定性。因此,本文借助贝叶斯理论引入模型参数的先验分布构建正则化项,以提高反演的稳定性,并在目标函数中加入改进的低频约束项,不仅得到了可靠的低频信息,还提高了反演的鲁棒性。由于反演的目标函数是有关模型参数的非线性公式,通常假定背景纵横波速度比为常数,而这种方法往往会降低反演精度,本文引入了重加权迭代算法来求解方程,在不断的迭代过程中更新背景值,以提高反演结果的精度。最后,将提出的新方法应用到了模型资料和实际资料中。对比结果表明该方法具有一定的可行性和实用性,提供了一种可靠的流体和岩性因子的直接提取方法。
1 方法原理
随着勘探程度的不断加深,非常规油气勘探成为了全球油气资源勘探的重要组成部分,其中,致密储层的勘探是非常规油气领域研究的热点问题之一[27]。Zhou和Hilterman[28]通过对大量实测数据分析,认为参数Russell流体因子F对固结碎屑岩储层的适用性最高,可以满足对具有低孔、低渗的特点、固结程度较高的致密储层孔隙流体的敏感指示。不同的流体具有不同的F值,因此根据流体项F可以区分干燥和饱和岩石以及饱和岩石中的流体类型;剪切模量μ代表了储层骨架的特性,表征了岩石的岩性特征,密度ρ也能显示储层的岩性特征,Goodway[8]提出两者的乘积μρ可以做为优质的岩性因子,有效地进行储层的识别。因此,利用纵横波叠前联合反演获取高精度的F和μρ,可以有助于解决致密储层识别和流体检测等问题。
1.1 FMD公式推导
叠前联合反演的理论基础是Zoeppritz公式,但是因为其表达形式复杂,许多学者对其进行了简化近似。Russell等人[29]基于孔隙弹性介质理论推导了基于Gassmann流体项f的纵波反射系数Rpp的线性近似方程,具体表达式如下:

上式中为纵波反射角和透射角的平均角度;γsat为上下层介质饱和岩石纵横波速度比的平均值;表示干岩石的纵横波速度比的平方,该值的具体计算方法可以基于实验室测量或者利用Gassmann方程的计算得到[10,30],具体到实际应用来说,应该根据研究区条件灵活选择估算方法,从而得到适用于研究区的数值;和Δµ分别为上下层介质剪切模量的平均值和差;f还可以表示为β2M,其中,β为Boit系数(抽空条件下每个单位体积变化中孔隙体积的变化),M为模量(在不改变孔隙体积的前提下,把流体压入地层孔隙所需要的压力),f和Δf分别为上下层介质Gassmann流体项的平均值和差。
Russell在Gassmann流体项基础上又提出了Russell流体因子F,其表达式为

公式(2)中Ip,Is分别为纵波阻抗和横波阻抗。
为了研究基于F、μρ和ρ的纵横波联合反演方法,首先根据孔隙介质理论推导基于这三个参数的的纵波以及转换波公式。针对纵波Rpp公式,我们首先从公式(1)的密度项提取公式(3)和公式(4)

则剩下的密度项为


公式(6)即为基于F、μρ和ρ的纵波近似系数表达式,在本文中称作FMD公式。
Aki和Richards[31]在入射角度较小且反射界面两侧的弹性参数变化不大的假设基础上推导了转换波Rps反射系数表达式:

公式(7)中,为转换波反射角和透射角的平均角度;、和分别为上下层介质纵波速度、横波速度和密度的平均值;ΔVp、ΔVs和Δρ分别为上下层介质纵波速度、横波速度和密度的差。已知横波速度与剪切模量和密度的关系式为根据微分性质可以得到则公式(7)可以改写为公式(8)
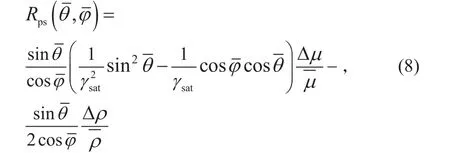
首先,从公式(8)的密度项提取公式(9)

则公式(8)中剩下的密度项为
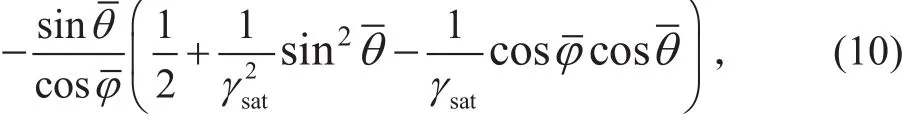
则公式(8)可以改写为FMD方程的转换波反射系数表达式:
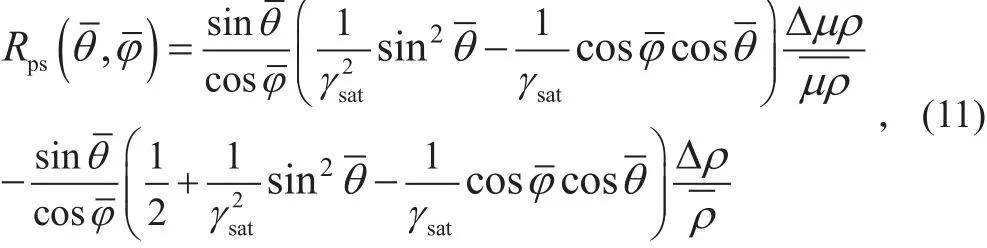
1.2 FMD公式精度分析
为了验证FMD公式的合理性,本文参考某致密砂岩储层的实测井数据,设计了两套模型对新推导的公式(6)、(11)进行精度分析。模型参数取值如表1所示,其中,模型1的两套砂岩层填充的孔隙流体均为水,上覆岩层的孔隙度为10%,下伏岩层的孔隙度为5%;模型2中两套岩层的孔隙度均为10%,但是上覆岩层的孔隙流体为气,下伏岩层的孔隙流体填充的是水。分别利用精确的Zoeppritz公式、Aki&Richards近似公式、Russell近似式以及本文新推导的FMD公式求取纵波反射系数,以及利用精确的Zoeppritz公式、Aki&Richards近似公式和FMD公式求取转换波反射系数,并进行对比。图1和图2分别是根据模型1和模型2数据得到的不同纵波反射系数、转换波反射系数曲线对比图。其中,黑色实线代表精确Zoeppritz公式,红色实线代表Aki&Richards公式,蓝色实线代表Russell公式,绿色虚线代表新推导的FMD公式。在图中可见,利用新公式求得的两套模型的纵波和转换波反射系数在35°内时与精确Zoeppritz公式得到的反射系数值误差非常小,并且在模型一中的求得的横波反射系数比Aki&Richards公式的精度要高一些。因此,FMD公式的精度在中、小角度入射情况下可以满足联合反演的要求,是直接提取相关弹性参数的理论基础。

表1 致密砂岩气储层模型参数Table 1 Parameters of gas reservoirs in tight sandstone
1.3 叠前联合反演方法
求解公式(6)和公式(11)时需要针对纵波数据以及转换波数据各联立M(M取大于等于3的整数)个方程,其中每个入射角θi(i=1,2…M)对应一个方程,假设每道有M个入射角度,N个采样点,设则公式(6)可以写作
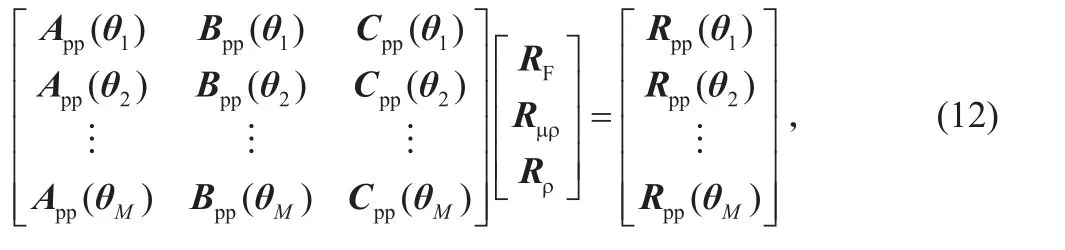
其中,

为了表达简便,公式(12)可以写为

其中,

同理,转换波公式可以改写为
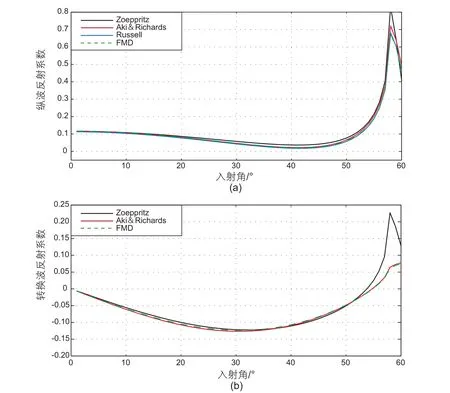
图1 模型1纵波反射系数(a)与转换波反射系数(b)对比图Fig. 1 Comparison of PP wave re flection coef ficients(a) and PS wave re flection coef ficients(b) of model 1

公式(14)中

其中,
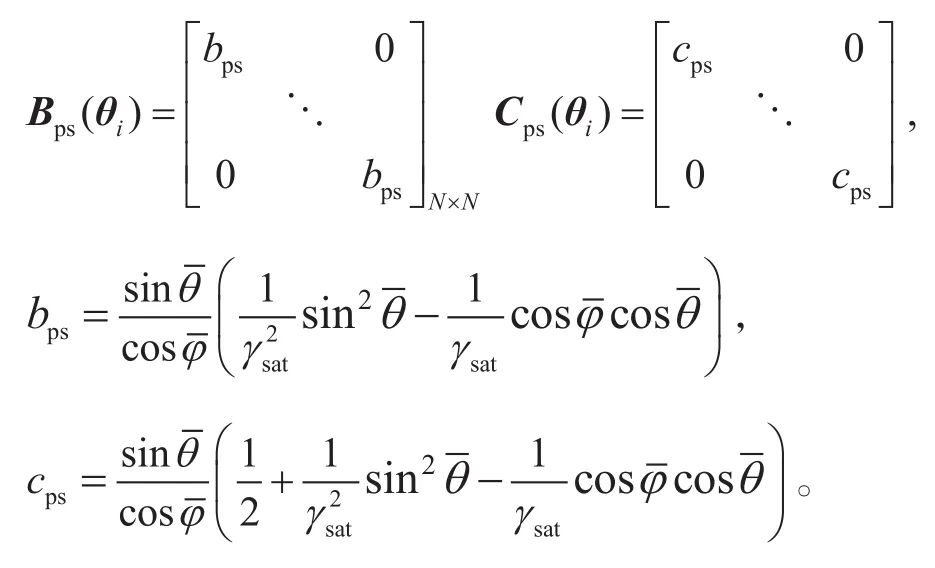
则通过求解公式(13)、(14)即可得到待求参数,但是在实际运算中公式(13)和公式(14)有较强的不适定性,因此本文借助贝叶斯反演[32],将模型参数的先验信息引入反演的正则化项中,可以有效地改善反演问题的不适定性问题。根据贝叶斯理论,模型参数的后验概率密度分布等于
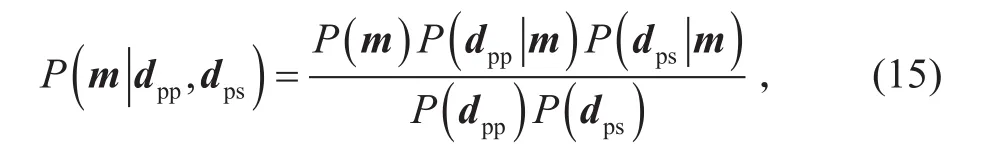
其中,P(m)为模型参数的先验分布;为似然函数,表征道集数据的噪声分布;当后验概率分布函数的形状不变的情况下,P(dpp)P(dps)为常数,可以忽略。
在面对实际资料时,叠前道集数据含有一定程度的噪声,本文假设噪声是互不相关的,均值为0且服从高斯分布的似然函数,纵、横波道集数据的噪声似然函数可表示为
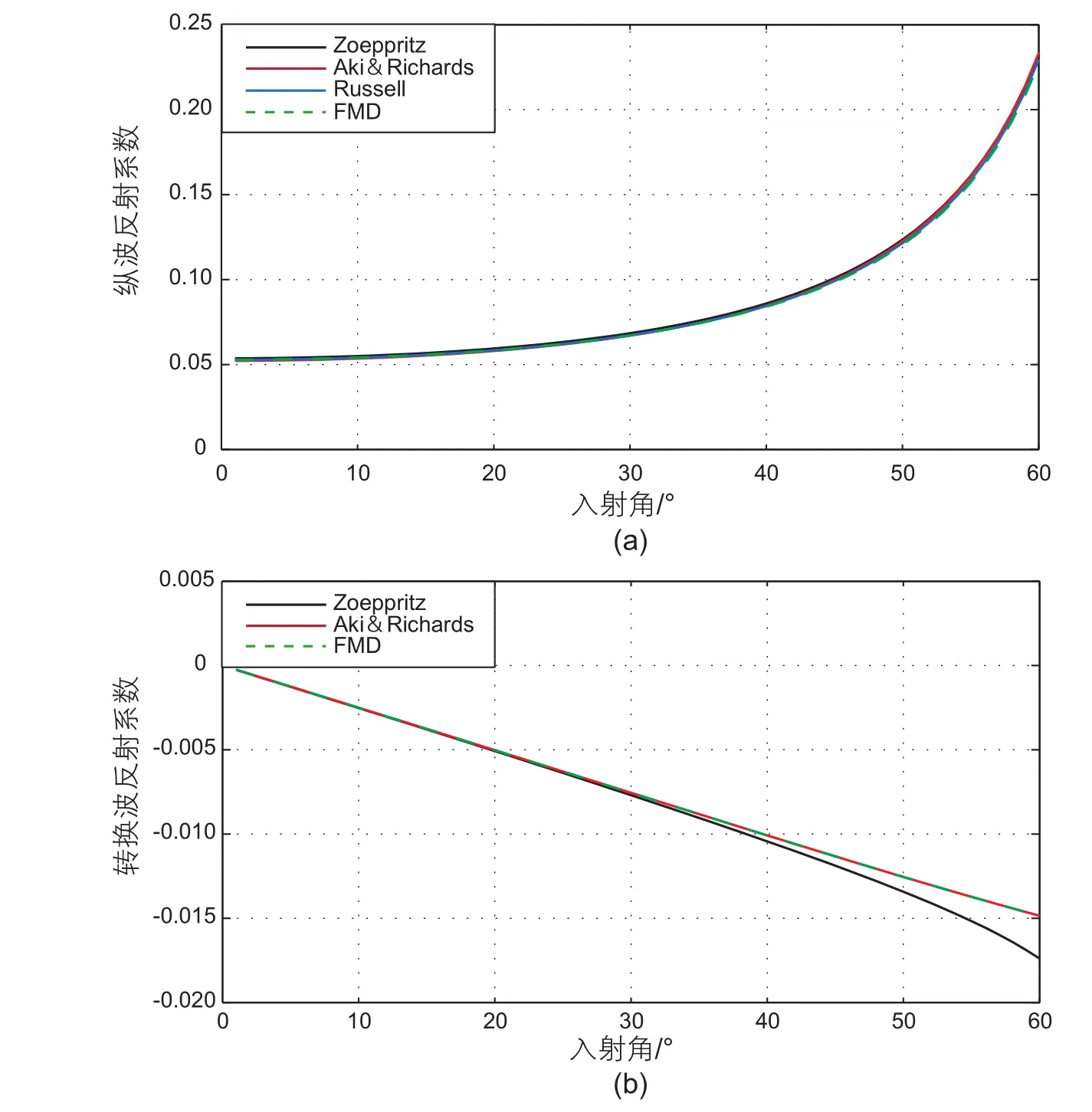
图2 模型2纵波反射系数(a)与转换波反射系数(b)对比图Fig. 2 Comparison of PP wave re flection coef ficients(a) and PS wave re flection coef ficients(b) of model 2

其中,Cnp=,Cns=分别为纵波数据和横波数据噪声的协方差;,分别为纵波数据和横波数据噪声的均方差;I为单位矩阵。
模型参数的先验分布可以分为单变量和多变量的,考虑到本文同时提取的三个参数的相关性,选取多变量分布可以降低由于三参数之间的相关性造成的反演病态问题。高斯分布仅可以产生一致性加权系数,这样会影响反演结果的稀疏性,而柯西分布可在求解过程中可以得到非一致加权系数,产生稀疏效果,更具有地质意义。因此,本文采用多变量柯西分布[33]作为模型参数的先验分布,具体公式为
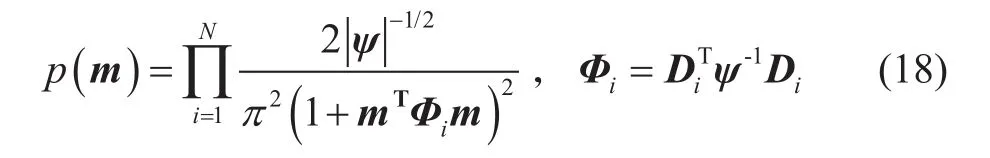
其中,ψ为相关矩阵,可以通过最大期望估计法得到[33]。Di为3N×3N的矩阵,其表达式为

把公式(16)、(17)、(18)带入到公式(15)中,可以得到模型参数的后验概率密度为

对公式(20)进行代数变换,便可以得到目标函数F(m),其中目标函数为

由于低频地震数据采集成本巨大,大多数的地区仍以常规采集为主,而常规采集中地震数据的低频信息受噪声影响严重,导致低频信息无法从地震数据中获得[34],因此反演过程中需要合并可靠的低频信息。低频信息不仅提供了反演参数的整体趋势,还增加了频带宽度,从而提高了反演结果的分辨率。因此,为了获得低频信息,还需要在目标函数中增加低频约束。常用的低频约束T如公式(22)所示

其中,PF,Pμρ,Pρ为积分矩阵,PFm,Pμρm,Pρm分别表示待求参数F、μρ、ρ的自然对数;LF,Lμρ,Lρ分别为真实的F、μρ、ρ自然对数的低频成分,可以由初始模型进行滤波得到;λF,λμρ,λρ分别为F、μρ、ρ的正则项的权系数。以F为例,

通常,在实际操作中,低频约束权系数的选择通常基于工程师的经验,通过不断修改加权系数来尝试获得最佳的反演结果。通过公式(22)可见,常规的低频约束是使反演得到的弹性参数的自然对数逼近模型的低频成分,这种约束方法对加权系数非常敏感,加权系数的选择不当则会影响反演结果的精度。因此本文在目标函数中引入了改进的低频约束T′,表达式如下所示

其中,HF,Hμρ,Hρ分别为弹性参数的低通滤波矩阵。可以看到改进的低频约束项使反演得到的弹性参数自然对数的低频成分逼近模型的低频成分[35],这种方法对加权系数相对不敏感,不仅降低了人为因素的干扰,还在反演过程中降低了对中、高频信息的影响,从而提高了反演精度。加入低频约束项后,新得到的目标函数为:

最后,可采用迭代重加权最小二乘来求解目标函数,在迭代过程中可以不断更新公式(24)中的得到F、μρ、ρ的反射系数,然后利用道积分即可得到F、μρ、ρ。
2 模型测试
为了验证本文提出的方法的可行性和抗噪性,本文选取了一组实测致密砂岩井数据进行测试。首先,在反演前对实测数据进行了Backus平均[36]处理,将数据从测井尺度转化为地震尺度,然后又进行了时深转换,使数据从深度域转换到了时间域。图3中蓝色实线表示处理后的实测井数据,黑色实线表示初始模型。然后,基于精确的Zoeppritz方程正演得到了实测井数据在不同采样时间和不同角度(5°,15°,25°和 35°)下的纵波和转换波反射系数,利用30 Hz的雷克子波与反射系数进行褶积,得到纵波以及转换波的角道集合成记录,如图4所示。为了验证本文提出的直接提取F、μρ、ρ方法的抗噪性,对合成记录加入了信噪比为2的高斯随机噪音,加入噪音后的角度道集合成记录如图5所示。
图6和图7分别为利用联合反演和仅利用纵波数据反演得到的结果与实测数据的对比,图中蓝色实线为理论值,红色实线为反演得到的值,黑色实线为初始模型,通过对比可见,虽然仅利用纵波数据也能得到合理的反演结果,但是三个参数的反演结果精度均低于联合反演结果的精度,因为纵波数据对横波和密度信息不敏感,而F、μρ、ρ参数均包含这两种信息,因此联合反演相对纵波反演可以有效提高F、μρ、ρ参数反演的精度。图8和图9为信噪比为2的情况下联合反演和纵波反演的结果,从图中可见在含有噪声的情况下,联合反演相对纵波反演同样可以得到精度更高的F、μρ、ρ的反演结果,具有较好的抗噪性。但是在实际应用中,大部分的情况下只有纵波数据,转换波数据比较少见,因此本文利用纵波反演方法进行了基于FMD公式直接求取弹性参数以及间接计算方法的对比。其中,间接计算是利用Aki & Richards近似公式反演得到纵波速度、横波速度、密度,然后利用它们计算得到F、μρ。图10为仅利用信噪比为2的纵波数据直接计算以及间接算得到的反演结果对比。为了更加清晰的对比,我们求取了图10中两种方法得到反演结果与理论值的相关系数(表2),其中相关系数指越大说明反演结果越趋近理论值,反演结果精度越高。从表中可以看到直接反演结果精度要高于间接计算得到的结果,因为直接反演可以有效避免间接计算引入的累积误差。
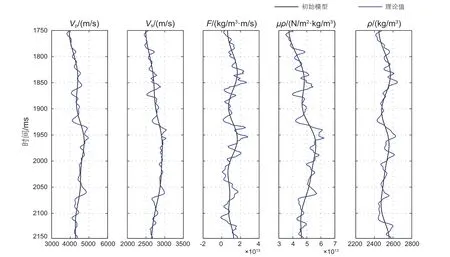
图3 理论井数据及初始模型Fig. 3 Theoretical well-logging data and the initial model for inversion

图4 合成角度道集;(a) PP波;(b) PS波Fig. 4 Synthetic angle gathers. (a) PP gathers; (b) PS gathers

图7 基于PP波数据反演结果与实测井数据对比(不含噪音)Fig. 7 Comparison of inversion results with real logging data base on PP-wave inversion (noise free).

图8 基于PP-PS波数据反演结果与实测井数据对比(S/N=2)Fig. 8 Comparison of inversion results with real logging data base on PP-PS joint inversion (S/N=2).

图9 基于PP波数据反演结果与实测井数据对比(S/N=2)Fig. 9 Comparison of inversion results with real logging data base on PP-wave inversion (S/N=2).
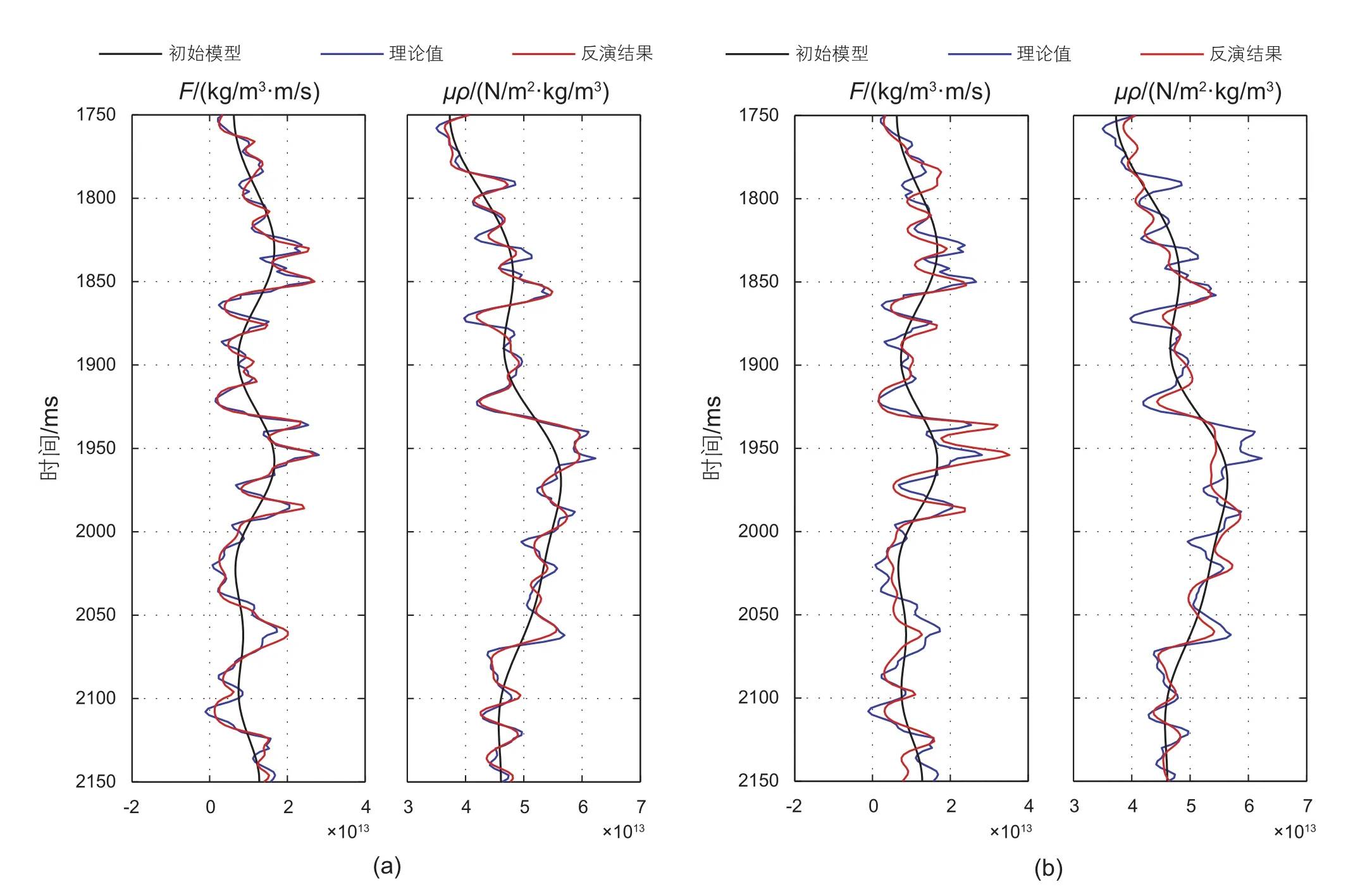
图10 直接反演结果与间接反演结果对比 (S/N=2);(a) 直接反演;(b)间接反演Fig. 10 Comparison of direct inversion results and indirect inversion results (S/N=2). (a) direct inversion;(b)indirect inversion

表2 反演结果相关系数统计表Table 2 Comparison of the correlation coefficients of the inversion results
3 实际资料测试
为了进一步验证FMD方程提取F和μρ参数的适用性,本文利用基于FMD方程的PP波反演和间接提取方法应用到了实际资料中。该研究区储层呈低孔、低渗特征,为典型的致密储层。首先,对保幅的叠前道集进行了预处理,并结合研究区实际情况,对叠前角度道集进行了分角度叠加,得到了 5°-15°,15°-25°,25°-35°的分角度叠加数据体(图11),图11(a)的剖面中黑色椭圆标记处有含气储层发育,图中黑色虚线所在位置为验证井所在位置。然后,利用层位数据和井数据建立初始模型。最后,基于纵波数据,分别利用本文提出的基于FMD方程的直接反演方法和常规的间接反演方法对研究区进行F、μρ参数的提取。

图12 反演结果对比剖面;(a) 新方法提取F;(b) 新方法提取μρ;(c) 间接计算F;(d) 间接计算μρFig. 12 Comparison of the inversion results.(a) inverted F by new method;(b) inverted μρ by new method;(c) inverted F by indirection method;(d) inverted μρ by indirection method
参数F能够反映流体的情况,参数μρ对储层岩性有一定的指示作用,因此在实际应用时,应将二者进行综合对比解释。通过岩石物理分析可知,研究区内含气储层具有低F和高μρ的特征。图12为反演结果对比图,其中图12(a)和图12(b)为基于FMD方程得到的反演结果,图12(c)和图12(d)为间接算得的结果,通过对图12(a)和图12(c)的对比可见,在黑色椭圆处发育的含气储层中,间接计算得到的参数F剖面图上含气储层响应不明显,而利用FMD方程直接求得的参数F结果在含气储层处有较为强烈的响应;在图中的黑色方框内部,间接计算得到的F出现了流体响应的假象,而直接计算的结果并未存在这种假象;因此,若按照图12(c)的结果进行油气藏描述,会导致烃类流体预测的失败;通过对图12(b)和图12(d)的对比可见,利用FMD方程直接计算得到的参数μρ相对间接计算,横向上更加连续,对于储层的细节刻画更加清晰(图中红色椭圆内部),有助于提高储层预测精度。
为了更加明确地看到两种反演结果的区别,本文在验证井的井点处(图11(a)黑色虚线)针对两套反演结果分别提取了伪井曲线,并使其与Backus平均处理后的实测井曲线做对比,如图13所示。通过伪井曲线的对比可见,利用FMD方程直接计算的方法提取的F、μρ参数与实际井曲线更加吻合。弹性参数的精度影响了储层和流体预测的精度,因此利用本文提出的基于FMD方程直接提取F、μρ参数的方法有助于提高油气藏描述的精度。

图13 伪井反演结果对比;(a) F;(b) μρ;Fig. 13 Comparison of the inversion results of the pseudo well.(a) F;(b) μρ;
4 结论
本文新推导的基于F、μρ参数的纵波、转换波反射系数方程精度满足反演需求,为直接提取F、μρ参数提供了理论依据;将贝叶斯理论和双项约束结合,直接从叠前数据中提取F、μρ参数是切实可行的,并且稳定了反演过程;通过数字模型和实际资料的测试对比验证了新方法的有效性,并且本文提出的反演方法相对直接求取方法有更高的抗噪性和精度,因此本方法具有较为广阔的应用前景;在提取参数F时涉及干岩石纵、横波速度比λdry的求取,而λdry参数的精度也影响了反演结果的精度,接下来还要进一步研究如何求的高精度的λdry值。

