非连续铺砂裂缝支撑机理及形变规律研究

陈星宇，尹丛彬，肖剑锋

中国石油川庆钻探工程有限公司井下作业公司，成都 610052

0 引言

我国在致密砂岩气、页岩气等非常规油气资源勘探开发领域近年来获得重要突破，初步评价表明我国非常规天然气资源量为(890～1260)×1012m3。以苏里格致密砂岩气藏为例，其储层具有低渗、低压、低丰度“三低”特征(渗透率介于 0.06×10-3～2×10-3μm2之间，压力系数为0.86，平均储量丰度为1.4×104m3/km2)，自然条件下无产能，需通过水力压裂改造改善储层渗流条件以获取工业产能。常规水力加砂压裂作为储层增产改造最为有效的技术手段之一，主要通过向地层连续泵注携砂液来确保压后获得人工支撑裂缝，以填砂裂缝内支撑剂颗粒的间隙作为油气渗流通道，但受储层闭合压力作用及支撑剂颗粒嵌入、破碎等因素影响，压后支撑剂颗粒间隙将被压缩，大幅降低了人工裂缝导流能力，因此改造效果往往达不到预期。同时，由于该区域致密砂岩气藏具有纵向砂体分布“薄、多、散、杂”、储层非均质性极强、储层高含水等压裂改造难点，压后多出现气井产量偏低、部分井气水同产现象严重、生产压力下降快、单井稳定产能低等问题，严重制约了该区块致密砂岩气藏的高效开发。

脉冲式加砂压裂在泵注阶段高频交替注入携砂液与压裂液，可在水力裂缝内非连续铺置支撑剂砂团，利用非连续砂团间裂缝开启空间作为油气流动通道，获得较连续充填人工裂缝高出若干数量级的导流能力，从而改善裂缝内油气流动效率，降低闭合压力及支撑剂嵌入等不利因素对长期导流能力的消极作用，为压后获得预期效果提供支撑。

研究表明，脉冲式加砂压裂的现场实施效果受压裂参数、储层物性及设备性能等多重因素影响。Fischer利用接触力学建立得到塑性材料应变特征基本方程[1]。Tinsley通过简化模型建立了缝内非连续铺砂压裂设计方法并取得了较好的现场应用效果[2]。Bazan等人在前人研究的基础上推导得到非连续支撑裂缝形变解析表达式[3]。Hou等人通过数值模拟计算发现脉冲式加砂压裂人工裂缝内支撑剂砂团横向间距与纵向间距相等时，同等条件下裂缝残余缝宽最大[4]。同时，Zheng等人采用串并联理论研究发现人工裂缝内支撑砂团内部渗透率可忽略不计，裂缝渗透率主要依赖于砂团间流动通道，且支撑剂砂团形状规整度将影响流体流动阻力[5]。页岩气储层缝网压裂时采用段塞泵注既可以降低摩阻，还可以提高裂缝导流能力[6-8]。以上研究主要围绕非连续支撑条件下裂缝一维形变规律展开，与现场施工参数结合程度较低，且未考虑缝内支撑剂砂团本身形变对裂缝残余缝宽(支撑剂砂团未支撑区域（砂团间隔区)受地层闭合压力作用后裂缝壁面间距）的影响，因此无法准确评价压后残余缝宽特征。笔者以非连续铺砂裂缝室内实验评价为基础，应用接触力学原理对裂缝中砂团支撑区域及未支撑区域形变展开研究，建立了三维空间内非连续支撑裂缝形变计算模型，同时结合储层岩石力学特征参数及现场压裂施工参数对裂缝形变规律展开计算分析，为脉冲式加砂压裂非连续铺砂裂缝优化设计提供了理论基础。

1 非连续多层铺砂技术原理

脉冲式加砂压裂依靠特殊混砂设备将含支撑剂的携砂液与压裂液高频交替注入，同时添加特殊纤维材料，以确保支撑剂段塞流动的稳定性。携砂液段塞与压裂液形成脉冲单元体，经密集多簇射孔孔眼二次分散后进入人工裂缝内形成非连续铺置，从而减小裂缝壁面接触面积，提高缝内有效孔道率，降低缝内流体的流动阻力[9-10]。同时缝内非连续支撑孔道将降低地层闭合压力、支撑剂颗粒破碎、嵌入以及残液滞留等因素对裂缝导流能力的伤害，从而减少支撑剂用量，并降低压裂施工作业风险，实现压后高产稳产的生产目标。

相较于常规水力加砂压裂[11]，脉冲式加砂压裂由于通过高频交替注入支撑剂段塞与压裂液，形成了非连续铺砂裂缝，并以缝内非连续铺置支撑剂砂团间的沟槽作为油气流动空间，其缝内流体流动状态与常规水力压裂连续铺砂裂缝的明显不同(见图1)。因此，如何确保支撑剂砂团间沟槽有效开启、降低压后未支撑区域的闭合风险是脉冲式加砂压裂工艺成功的关键。

图1 缝内油气流动特征对比(左：常规加砂压裂；右：脉冲式加砂压裂)Fig. 1 Comparison of oil & gas flow charcteristics between conventional fracturing and high-frequency plug fracturing

2 非连续支撑壁面稳定机理研究

脉冲式加砂压裂水力裂缝内支撑剂砂团呈非连续分布状态。压裂施工结束后随着缝内净压力减小，支撑剂砂团在地层闭合压力作用下将出现轴向压缩和径向扩展，同时在缝内未支撑区域裂缝壁面将发生一定程度的弯曲变形(见图2)。因此，对于非连续支撑裂缝而言，缝内油气流动通道是否长期有效取决于缝内非连续铺置支撑剂砂团受压形变程度及未支撑区域形变后残余的有效缝宽。在支撑剂砂团稳定性评价实验的基础上，建立非连续铺置支撑剂砂团受压变形计算模型及未支撑区域裂缝壁面形变计算模型，以此评价储层闭合压力作用下支撑剂砂团受压变形规律及未支撑区域裂缝壁面形变特征，为优化脉冲间隔时间等压裂设计参数提供理论依据。

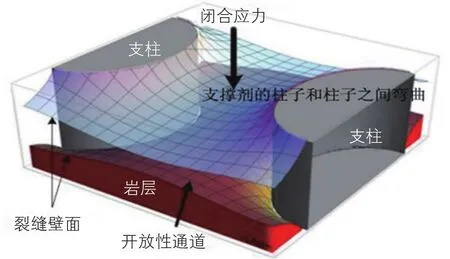
图2 地层闭合应力作用下裂缝壁面变形示意图Fig. 2 Deformation of fracture under formation closure stress

2.1 支撑剂砂团受压稳定性

在脉冲式加砂压裂过程中，由于支撑剂颗粒基本处于饱和液体环境中，颗粒间黏结力可忽略不计。伴注纤维在高黏度携砂液的作用下相互缠绕形成的空间网状结构(见图3)，对支撑剂砂团形成有效包裹，后期随压裂液返排，在储层闭合压力作用下砂团将被逐渐压实。

实际单位脉冲周期内，支撑剂段塞进入水力人工裂缝后其形态为不规则形态，在同一携砂液砂浓度条件下各支撑剂砂团质量相等。因此，计算中将现场实际不规则形态支撑剂砂团简化为等径圆柱状支撑剂砂团，并通过支撑剂砂团制备模具将20/40目携砂液制成等径圆柱状支撑剂砂团，经恒温箱高温烘干后放入API导流室垫片上，使用油压机测定不同闭合压力作用下支撑剂砂团轴向受压形变量。实验参数见表1。

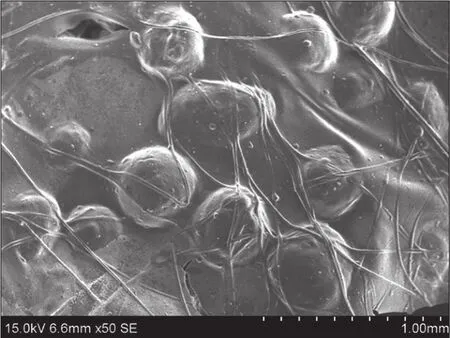
图3 纤维压裂液环境中支撑剂颗粒分布图Fig. 3 Proppant grain distribution in fiber fracturing fluid

表1 支撑剂砂团压缩变形实验参数表Table 1 Parameters of proppant sand pillar compressive deformation tests

实验结果表明，随闭合压力增加，人工模拟裂缝内非连续铺置支撑剂砂团主要经历前期径向扩展和后期轴向压实两个过程，后期轴向压实决定了支撑剂砂团半径以及砂团间的导流空间(见图4～图6)。

保持支撑剂砂团体积不变，利用岩土力学中邓肯—张本构模型[12]对实验数据进行拟合，可得到支撑剂砂团扩展半径与闭合压力及携砂液砂浓度关系方程。

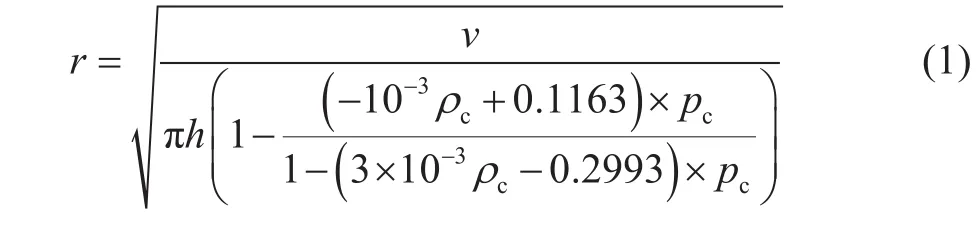
式中，r表示砂团扩展半径，mm；pc表示闭合压力，MPa；v表示支撑剂砂团体积，mm3；h表示支撑剂砂团初始高度，mm；ρc表示携砂液砂浓度，kg/m3。

图4 非连续铺砂裂缝受压前铺置图Fig. 4 The discontinuous sanding fractures before compression

图5 非连续铺砂裂缝受压后支撑剂砂团形态Fig. 5 Shape of proppant sand pillars in discontinuous sanding fractures after compression

2.2 未支撑区域裂缝壁面形变计算模型

支撑剂砂团体积主要受携砂液脉冲泵注时间、携砂液砂浓度及泵注排量等参数影响，未支撑区域体积由压裂液脉冲泵注时间及泵注排量决定。综合支撑剂砂团受压形变特征实验研究结果及弹性半空间形变基本方程，建立非连续铺砂裂缝综合形变计算模型，对砂团支撑区域及未支撑区域裂缝壁面形变展开定量计算。

储层闭合压力条件下，缝内支撑剂砂团支撑区与未支撑区呈现不同的形变特征。砂团形变特征由前文所述数学方程进行表征，未支撑区裂缝壁面形变特征通过接触力学弹性半空间内形变量计算方程描述。

将储层闭合应力沿人工裂缝面(缝长、缝高、方向)展布简化为均匀分布状态(见图7)，根据接触力学基本原理[13-14]，在弹性半空间中形变量随位置的分布所遵循的基本方程为：

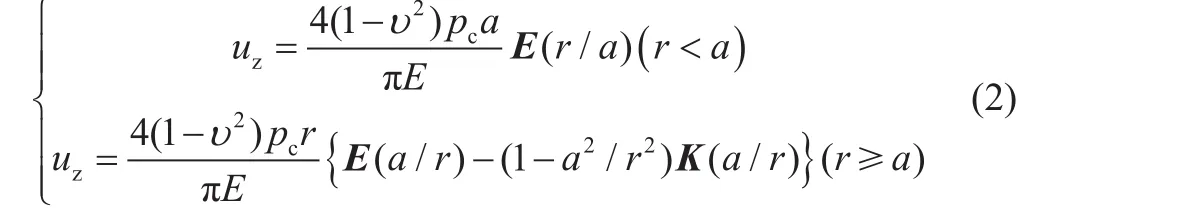
式中，E(r/a)是模为(r/a)的第二类完全椭圆积分，K(a/r)是模为(a/r)的第一类完全椭圆积分，E(r/a)的展开式如式(3)所示。

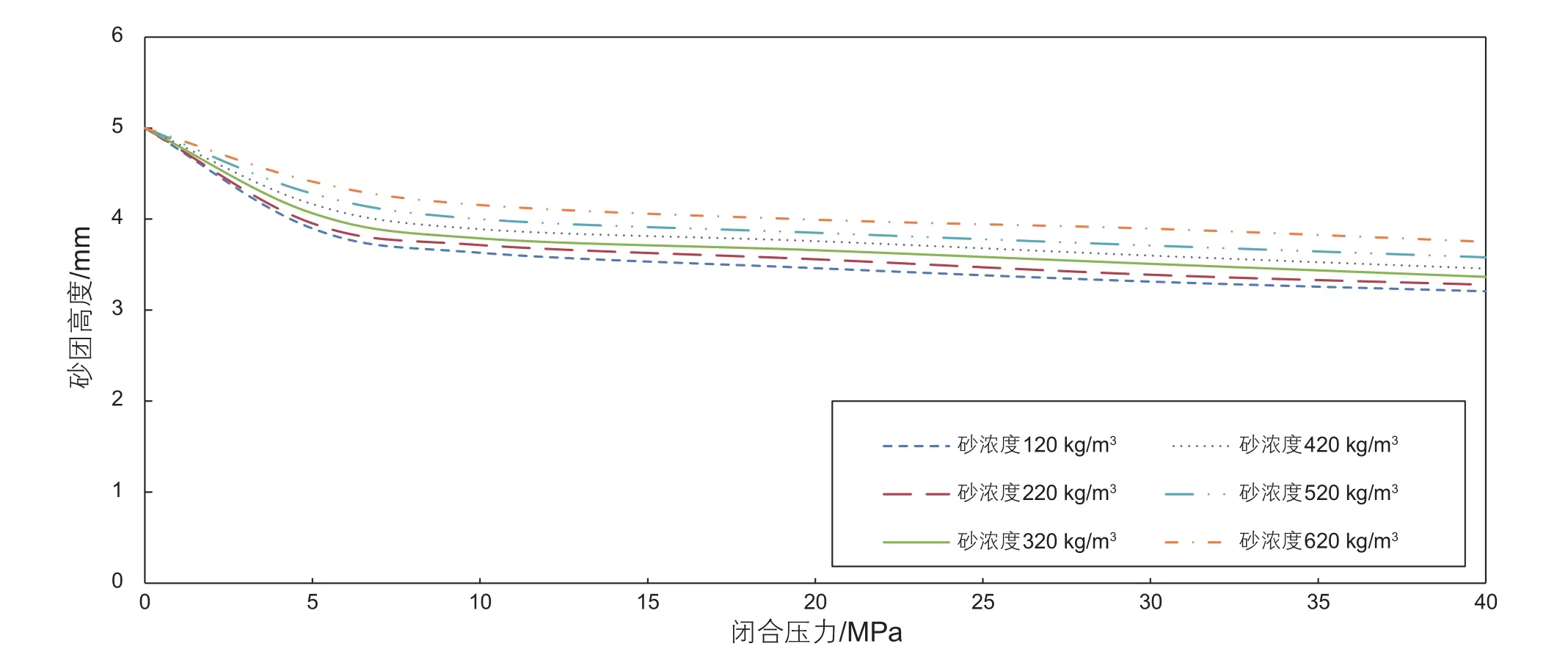
图6 支撑剂砂团受压形变规律曲线图Fig. 6 Deformation curves of proppant sand pillar under compression

其中，uz表示形变量，mm；υ表示泊松比；E表示杨氏模量，MPa；a表示砂团受压扩展后的半径，mm；r表示形变计算点距离砂团的中心距离，mm。

因躯体感觉系统疾病或者损伤造成的慢性疼痛就是神经病理性疼痛（neuropathic pain，NeP），有着较高的发病率，其中脊髓损伤患者发病率最高，可以达到70%。作为疼痛传导调节受体，N-甲基-D-天冬氨酸受体（N-methyl-D-aspartate receptor，NMDAR），可以将神经元对于疼痛刺激敏感度提高，通过将自身受体活性改变的方式，还能将周围神经免疫细胞激活，通过将大量炎性因子释放出来，在这种作用及改变下，会将重要的Nep机制产生，即痛觉过敏。下面将具体对神经病理性疼痛中NMDAR受体作用分析。

将缝内非连续分布支撑剂砂团简化为圆形柱状均匀分布(见图8)，以单位脉冲周期内砂团及周围未支撑区域作为计算单元。忽略支撑剂颗粒及压裂液压缩性，单元体内支撑剂砂团体积及压裂液体积的几何关系满足体积守恒原理，如下式：

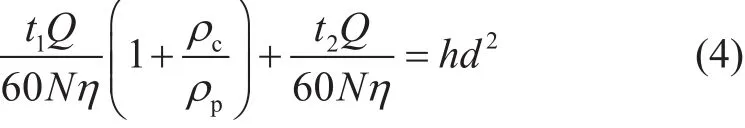
图7 半平面裂缝形变图Fig. 7 The fracture deformation in half space

其中，t1表示携砂液段塞时间，s；t2表示压裂液段塞时间，s；Q表示排量m3/min；ρc表示携砂液砂浓度，kg/m3；ρp表示支撑剂体积密度，kg/m3；N表示射孔孔眼数；η表示射孔有效率；d表示砂团间距，mm。

接触力学[13]中接触点形变基本方程是建立在一维条件上的，在裂缝平面形变计算时需要将一维模型进行扩展。根据公式(3)可以计算得到不同施工参数条件下砂团几何尺寸及相对位置，以各个砂团中心为原点，对裂缝平面各点与各砂团原点的距离进行计算，在此基础上利用形变模型积分，可以得到平面各点形变量，通过叠加多砂团对裂缝形变的影响，最终得到模型内支撑区域和未支撑区域内各点的三维综合形变结果(见图 9)。

3 算例分析

由支撑剂砂团受压形变拟合方程及缝内未支撑区域裂缝壁面形变计算模型分析可知，储层岩石力学参数、单位周期内脉冲时间及携砂液浓度等参数对压后非连续铺砂裂缝有效开启程度有直接影响，压裂设计参数与储层特征参数的合理匹配将有利于获得更大的残余缝宽。以苏里格地区某区块致密砂岩气藏为例，利用三维裂缝形变计算模型对未支撑区域裂缝壁面形变规律展开计算。

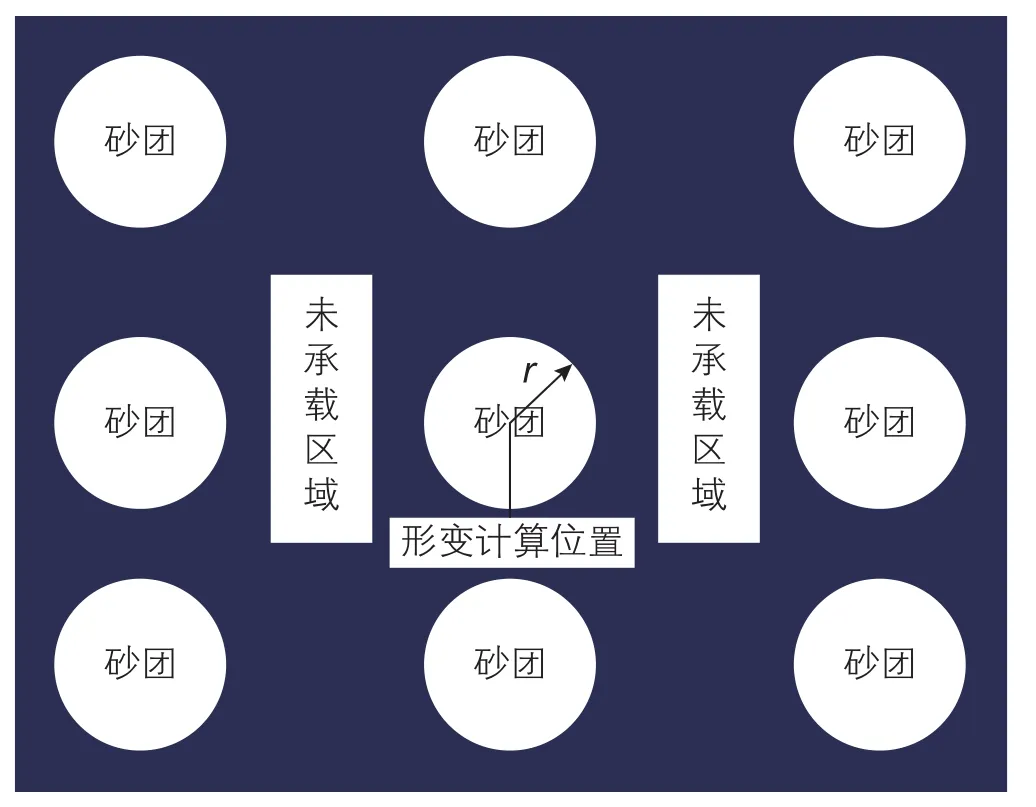
图8 平面裂缝形变计算示意图(砂团为圆形砂团)Fig. 8 Figure of two-dimensional deformation of discontinuous sanding fracture(the shape of sand group is de fined as circle)

表2 算例基本参数Table 2 Parameters of simulation example

3.1 脉冲时间与泵注排量的影响

由式(2)可知，脉冲周期决定了支撑剂砂团及未支撑区域体积大小(动态缝宽条件下)—成正比关系，但尚未研究闭合应力作用下裂缝形变及残余缝宽(决定后期油气流通通道)的变化规律及一定条件下临界取值[15]。

利用matlab数值编程软件对不同脉冲时间、泵注排量下支撑剂砂团尺寸及未支撑区域裂缝壁面变形展开计算，模型基本参数见表2，脉冲时间取现场实际常用范围8～22 s，泵注排量2 ～6 m3/min。模拟计算结果见表3和表4。

由计算结果可知，随脉冲间隔时间、泵注排量增大，支撑剂砂团体积及未支撑区域体积均增加，此时支撑剂砂团支撑区域裂缝接触闭合风险将减小，但由于未支撑区域体积增大将加剧该区域裂缝壁面弯曲变形程度，该区域接触闭合的风险将增大。

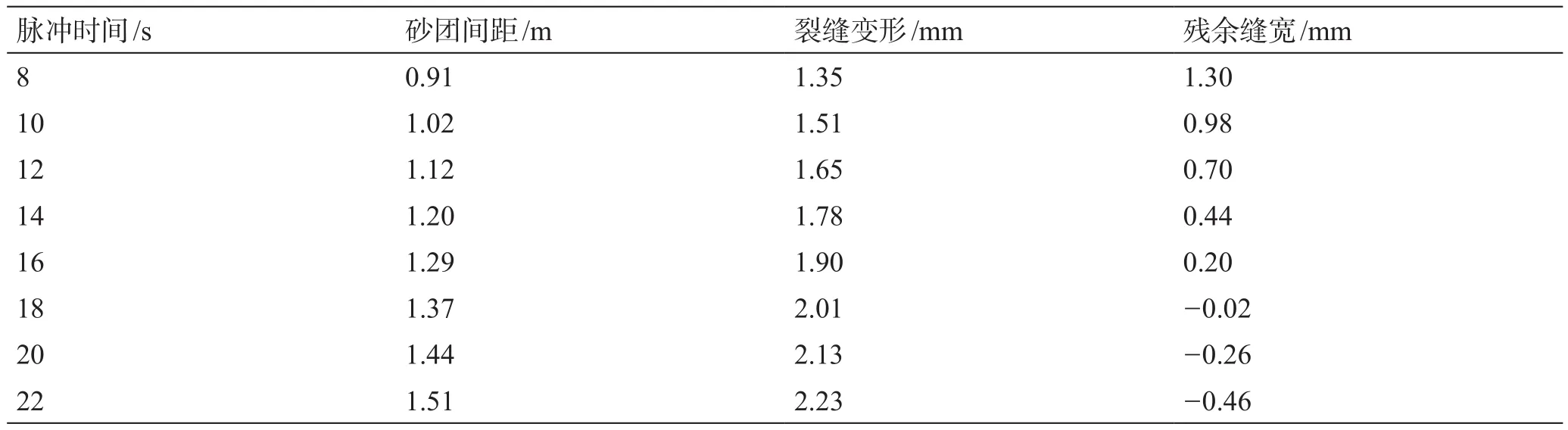
表3 不同脉冲间隔时间下残余缝宽计算结果Table 3 Simulation results of residual width with different pulse intervals

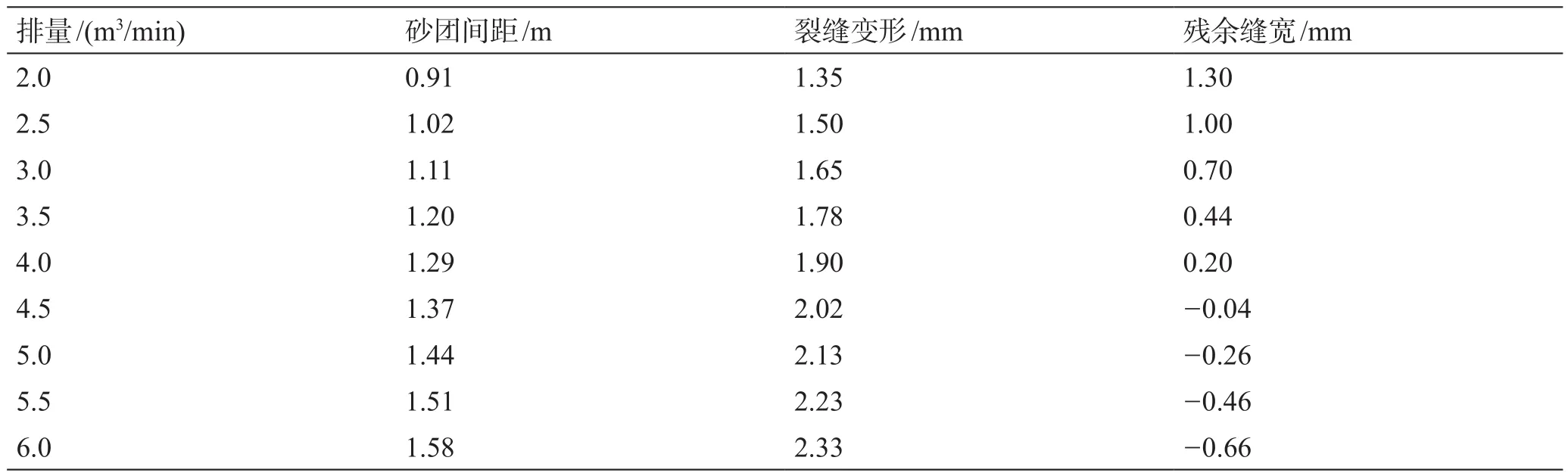
表4 不同排量条件下残余缝宽计算结果Table 4 Simulation results of residual width with different pump rates

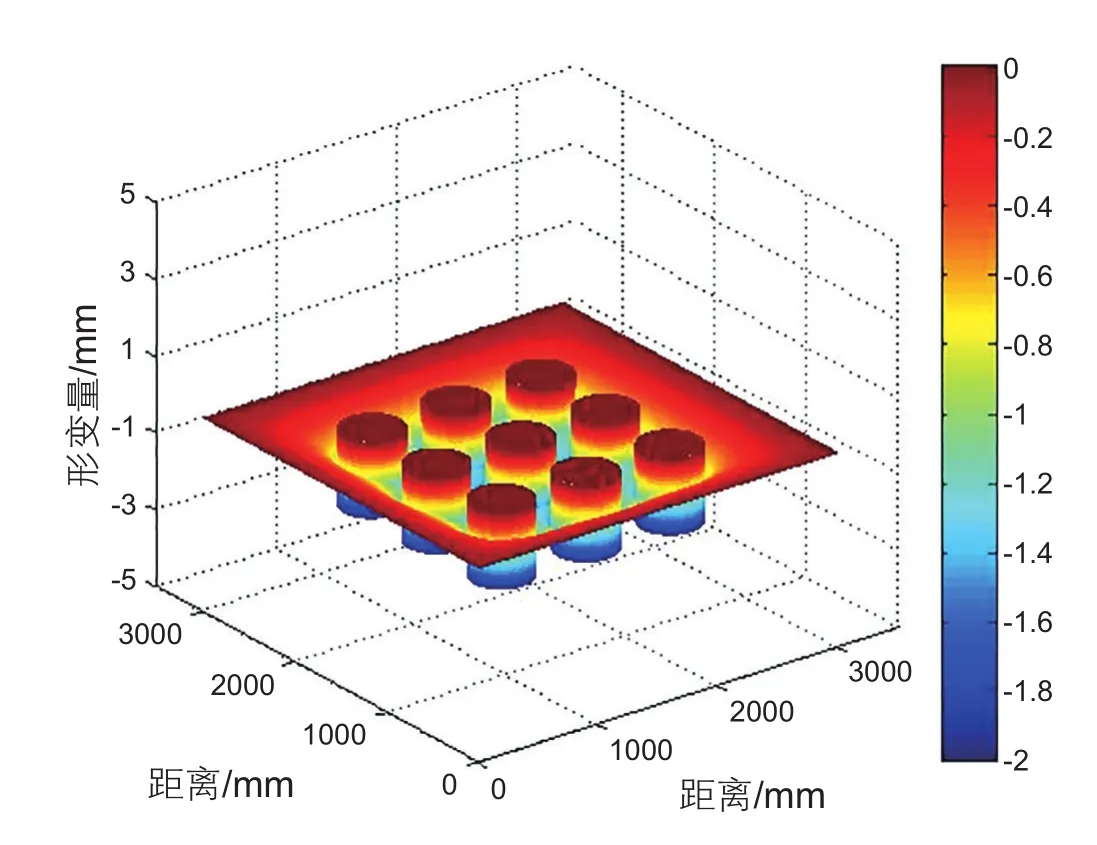
图9 未支撑区域裂缝壁面形变量三维场图Fig. 9 Three-dimensional deformation quantity of unloaded fracture area

对比不同脉冲时间及泵注排量下裂缝形变曲线和计算结果可知(见图10～图11)，在弹性半空间裂缝受压情况下，砂团不同位置在轴向上变形程度差异较大，在砂团半径范围内，计算位置距离砂团中心越远，砂团形变趋势越快。而在未支撑区域裂缝形变趋势则逐步减缓，可以看出砂团的形成能够一定程度减少裂缝未支撑区的闭合，但是不同脉冲时间所形成的砂团在降低裂缝闭合能力上有较大差别。在携砂液砂浓度为320 kg/m3，排量为3 m3/min，裂缝宽度为4 mm条件下，当脉冲时间超过18 s时，裂缝变形量超过2 mm，裂缝残余宽度降低至负值，即裂缝存在闭合风险；而在其他参数不变的条件下，排量超过4.5 m3/min时，未支撑区域残余缝宽为负值，即沟槽区域出现闭合。因此，为确保非连续支撑裂缝支撑剂砂团未支撑区域压后处于开放状态，推荐现场实施脉冲时间范围为8～16 s，施工排量不超过4.0 m3/min。

3.2 携砂液砂浓度影响

携砂液砂浓度改变时，支撑剂砂团抗压能力即裂缝支撑效果将随之改变。研究携砂液砂浓度与非连续铺砂裂缝未支撑区域残余缝宽的定量关系有助于优化压裂设计参数。保持计算模型其余参数不变(见表2，脉冲时间取12 s)，携砂液砂浓度在120～620 kg/m3时，计算未支撑区域裂缝壁面形变量。计算结果见表5、图12。

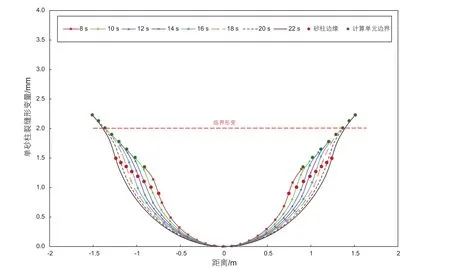
图10 不同脉冲时间裂缝形变曲线Fig. 10 Curve of fracture deformation with different pulse intervals

图11 不同排量裂缝变形曲线Fig. 11 Curve of fracture deformation with different pump rates

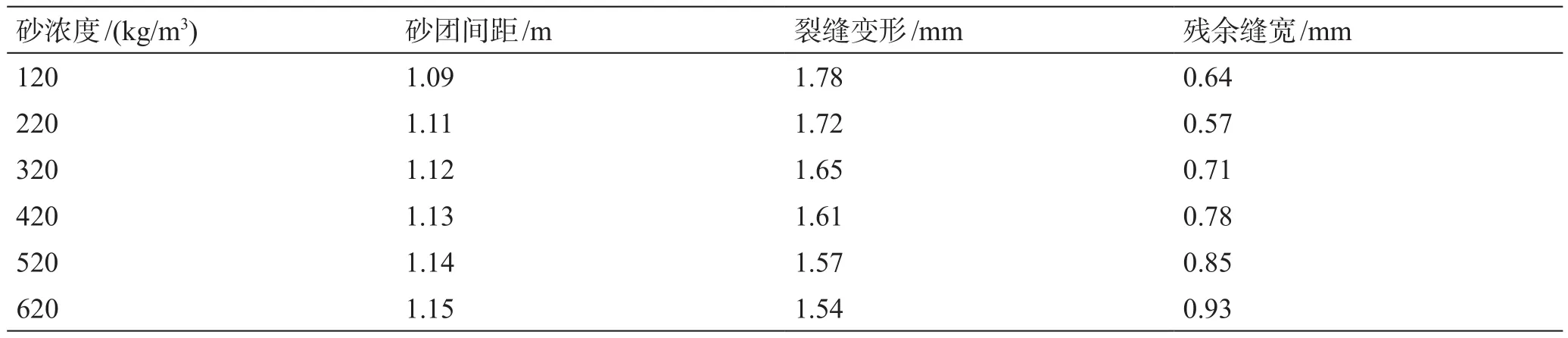
表5 不同携砂液砂浓度条件下残余缝宽计算结果Table 5 Simulation results of residual width with different carrying fluid concentrations

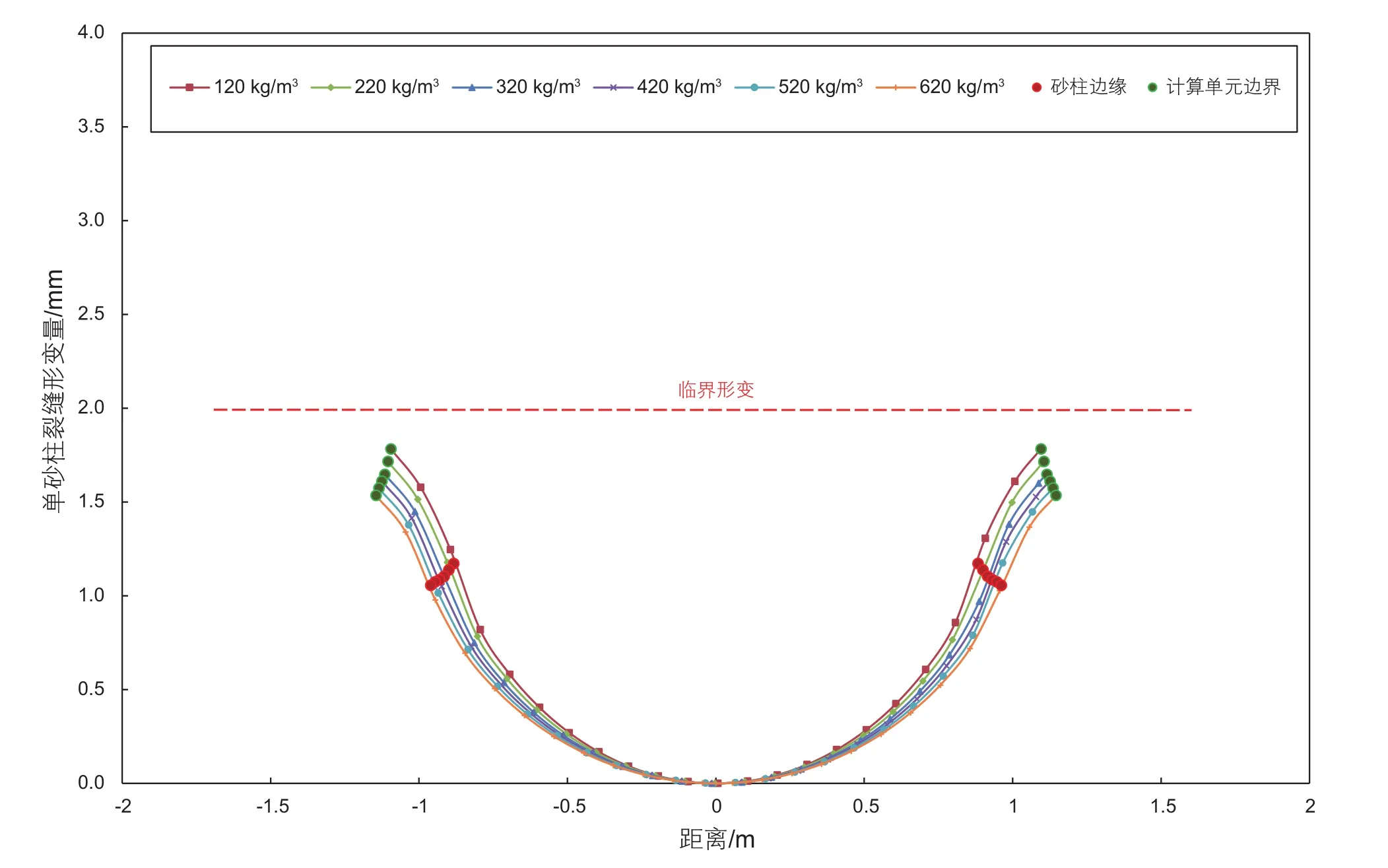
图12 不同携砂液砂浓度裂缝变形曲线Fig. 12 Curves of fracture deformaiton with different carrying fluid concentrations

由计算结果可知，携砂液浓度增加时，支撑剂砂团体积将随之增加，脉冲间隔时间保持不变时，未支撑区域几何尺寸将随之减小，支撑剂砂团与未支撑区域裂缝壁面形变量均减小。当裂缝初始缝宽为4 mm，脉冲间隔时间为12 s，携砂液砂浓度增加至620 kg/m3时，未支撑区域裂缝壁面形变量小于初始半缝宽值，此时非连续铺置支撑剂砂团间沟槽仍处于开启状态，即携砂液浓度对裂缝壁面形变影响较小。但随携砂液砂浓度增大，压裂施工砂堵风险也随之增加，因此现场工艺实施过程中携砂液浓度应根据储层条件及施工压力响应调整。

3.3 岩石力学参数影响

由接触力学原理可知，非连续支撑裂缝缝内砂团及裂缝壁面形变量受地层岩石杨氏模量及泊松比影响。据式(3)分析可知，杨氏模量与泊松比合并处理后得到有效杨氏模量，表达式如下：

式中，E′表示岩石有效杨氏模量，MPa，E表示杨氏模量，MPa，υ表示泊松比。

在其余参数不变的条件下(见表2，脉冲时间取12 s)，计算不同有效杨氏模量对非连续支撑裂缝残余缝宽值的影响，结果见表6、图13。据计算结果分析可知，同等受力条件下，有效杨氏模量增高，岩石弹性性能增强，未支撑区域裂缝壁面形变量减小，其残余缝宽增大。同时改变脉冲间隔时间，计算不同有效杨氏模量条件下，压后非连续支撑裂缝未闭合的临界值，得到脉冲时间与有效杨氏模量的关系图，见图14。

分析有效杨氏模量—临界脉冲时间关系图可知，在给定储层条件下，随储层有效杨氏模量增加，临界脉冲时间相应增加，即储层刚性相对较强时，较长的脉冲间隔时间，使未支撑区域裂缝壁面较刚性较弱的储层更不易接触闭合，这可为压后生产流体流动提供更为高效的流动通道。

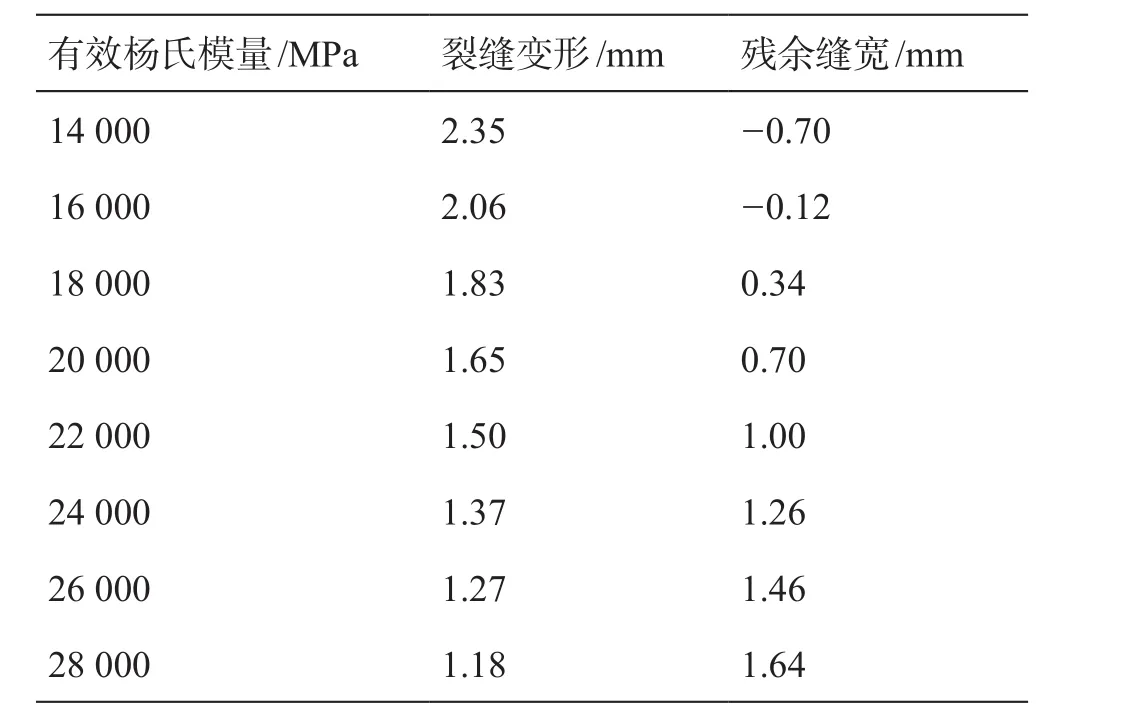
表6 不同有效杨氏模量模拟计算结果Table 6 Simulation results with different effective Young modulus

图13 不同有效杨氏模量裂缝变形曲线Fig. 13 Curves of fracture deformation with different effective Young modulus

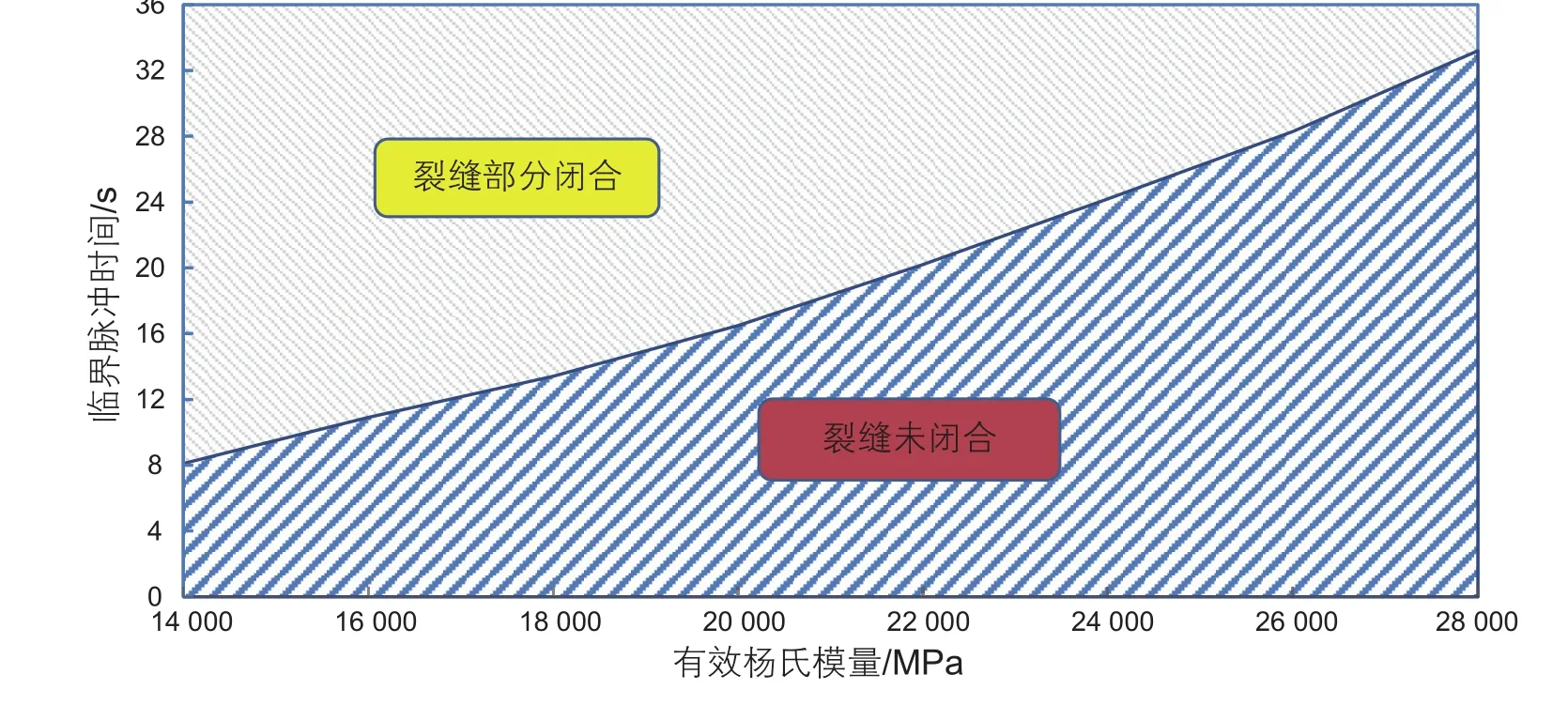
图14 有效杨氏模量—临界脉冲时间关系Fig. 14 Relationship between effective Young modulus and critical value of pulse interval

4 结论

(1)支撑剂砂团的室内受压稳定性实验表明，随着闭合压力增大，人工模拟裂缝内非连续铺置支撑剂砂团主要经历前期径向扩展和后期轴向压实两个过程。前期过程主要影响未支撑区域几何空间大小，后期轴向压实则对非连续支撑裂缝稳定性影响更大。

(2)所得非连续支撑裂缝和压后未支撑区域裂缝残余缝宽受储层闭合压力、岩石杨氏模量、泊松比及支撑剂砂团尺寸、砂团间距等因素影响。利用接触力学计算模型可定量评价给定储层条件下支撑剂砂团、砂团间距、岩石力学参数、泵注参数等因素对残余缝宽的影响。

(3)计算实例结果表明：泵注排量及脉冲时间对压后未支撑区域裂缝残余缝宽影响趋势一致，随泵注排量、脉冲间隔时间增大，支撑剂砂团稳定性增加但未支撑区域闭合风险增大。岩石有效杨氏模量越大，未支撑区域裂缝壁面形变量越小，裂缝闭合风险越小。携砂液砂浓度较高时压裂施工砂堵风险增大，因此现场实施过程中携砂液浓度大小应根据储层条件及施工压力响应调整。

(4)苏里格致密砂岩气藏直井压裂改造多采用油管分级压裂模式，结合裂缝残余缝宽模拟计算结果，建议脉冲式加砂压裂的脉冲时间控制在8～16 s，以确保非连续铺砂裂缝未支撑区域保持有效开放。