水力压裂微地震监测中应力场的复杂性对应力反演的影响

陈筱青，王润秋*，江勇勇，黄炜霖，储仿东，尹陈

1 中国石油大学(北京)油气资源与工程国家重点实验室，北京 102249

2 中国石油集团东方地球物理勘探有限责任公司，涿州 072751

3 中国石油集团川庆钻探工程有限公司，成都 610051

1 引言

微地震监测是水力压裂中用于估计岩层情况的一种技术[1]，从20世纪六十年代开始就广泛应用于油气储层动态监测和煤矿开采等诸多领域[2-7]。微地震监测的诸多任务中很重要的一项就是震源机制和应力状态的研究，其目的在于阐明微破裂的起因并且更好地认知裂缝状态[8-10]，裂缝的破裂和发育还与岩石中的应力方向密切相关[11]。对震源破裂过程定性和定量的研究能够有效地优化压裂方案和储层改造，从而提高油气井的采收率。

在很多情况下，水力压裂过程中微地震的产生是由于地应力场的扰动或地层压力的变化。当高压液体注入岩层中会使地下孔隙压力大于地层的最小主应力，以至于裂缝或者破裂面上的有效主应力减小，这样就会破坏围岩和断层的稳定性，从而产生很多破裂或者活化之前已有的断层[12]。应力场不仅影响了油气田注水过程中自然裂缝的发展，还与井位优化、人工裂缝的方向和流量有着密切的关系。因此，在制定压裂方案时应该考虑到压裂区域的应力状态，其在水力压裂的形式和延伸方向上的确定性，可以防止裂缝失稳并有效地控制液体流向。

在求解应力场的探索过程中，前人提出许多方案。Anderson通过分析断层系统的动力学机制构建了古应力轴的方位，之后定量的研究应力主轴方向便成为了主要的研究方向[13]。最早开始研究剪切应力与断层几何关系的是Wallace[14]，之后Bott通过研究应力张量与断层滑动的关系提出了断层滑动方向与断层面上剪切应力方向一致性的假设[15]，后人将这两人的观点合并称为Wallace-Bott假设，并作为之后大多数求解应力场方法的基本出发点[13]。在这一假设的基础上，Angelier系统地利用出露地表的断层擦痕来求解应力场的主轴方向[16]；Etchecopar充分利用地表的断层节理数据，通过网格搜索算法来反演应力张量[17]。

在前人提出的一系列求取应力状态的方案中，其中广泛应用的一种方法是由震源机制反演应力状态。Michael在1984年提出了一种最容易实现的线性反演方法，该方法假设所有断层面上的剪切应力为常值，并且认为这些断层都是由相同的构造事件诱发[18]。同时，Gephart和Forsyth[19]利用网格搜索的方法做了大量工作，通过对比不同的参考坐标轴而不是比较破裂面上剪切应力和滑动向量方向的差异，从而在整个解空间搜索最优解。他们还将应力张量转换到主轴坐标系中并根据主轴应力大小(特征值)定义了形状因子R。形状因子可以明确地表示出三轴主应力的相对大小[19]：

σ1，σ2，σ3分别表示最大、中间和最小主应力。因此形状因子R的变化范围是0～1，它控制了应力椭球的形状。如果σ2和σ3近似相等，那么R接近于1，这就意味着震源是单轴压缩；如果σ2和σ1近似相等，那么R接近于0，这就意味着震源是双轴压缩[20]。在此之后，Angelier提出了一种剪切应力滑动分量方法SSSC[21](Shear Stress Slip Component)，该方法是寻找能够使剪切应力滑动分量值最大的应力张量。他定义剪切应力滑动分量向量为剪切应力向量在滑动方向上的正交投影，使剪切应力滑动分量最大就意味着剪切应力平行于滑动矢量。

上述根据震源机制求解应力场的3种方法基于几个共同的假定：(1)断层沿分解的剪切应力方向滑动；(2)岩石具有均匀的物理特性；(3)震源机制的独立性[22]。基于之前的理论，Abers和Gephart利用不同地震事件的初动通过搜寻主应力轴的方向同时反演应力张量和每个震源机制[23]。然而，根据震源机制反演应力的方法都面临着同一个难题，就是如何从两个正交节面中选取真实的断层面。Michael进行了一系列的数值实验发现，断层面的不确定性会直接影响到求取应力张量的准确性，还会导致形状比扭曲[24]。为了解决这一难题，Vavryčuk提出根据断层面的不稳定性来识别真实的断层面，即在已知的应力状态下选取更不稳定的节面作为真实的断层面[25-26]。他将断层面的不稳定性这一约束运用到Michael的线性反演方法中，使反演结果的准确性得到了显著的改善。

这些反演方法大多是以震源机制为基础求取一个最优的应力模型，使之最大程度上符合所有的破裂面。然而在微地震监测中，由于水力压裂裂缝的尺度相对较小，并且分布形态又较为复杂，所以很难求取一个理想的应力模型使之符合研究区域中所有的破裂状态，最根本的原因是由于水力压裂过程中应力状态较为复杂，均一性较差。Hardebeck和Michael在2006年提出了阻尼区域尺度应力反演来研究区域应力状态的时间-空间变化[27-28]。他们的方法将研究区域或者时间划分成一些小分区，在所有的分区中同时反演应力状态，并且通过选取合适的阻尼因子使得相邻分区反演的应力方向差异最小[29]。这种方法大大改善了由于时空变化较大对应力反演的影响，但是在水力压裂微地震监测中，由于研究区域较小，且微地震事件的分布十分密集，如何对观测事件进行有效的空间划分还需要深入探究。为了确定水力压裂过程中应力场的复杂性对应力反演结果的影响以便更好地解决这一问题，本文将模拟均一应力场条件下和复杂应力场情况下的震源机制解，通过应力反演得到对应的应力模型并分析反演结果的误差值。另外分析了加入不同水平的噪声以及应力场在不同复杂程度的条件下反演结果产生的误差情况。为了避免由于断层面的不确定性造成的反演误差，本文在应力反演过程中采用的是Vavryčuk的迭代联合反演方法[25-26]。

2 应力反演方法

Michael的线性反演方法是Vavryčuk的迭代联合反演方法的基础[25-26]，基本思想是求取一个应力张量使得剪切应力分量与每个断层面上的滑动分量夹角最小。Michael假设断层面上剪切应力的方向向量N就是剪切运动的滑动方向s，用矩阵形式可表示为[18]：

其中，G是根据每个震源机制的断层法向向量n求取的矩阵，并且可以扩展到已知断层方向和滑动方向的K个震源机制。

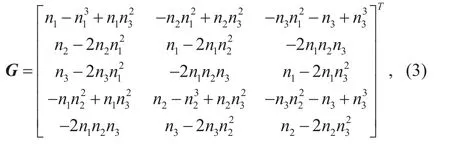
法向向量n可以根据震源机制解的走向φ、倾角δ和滑动角λ求取：

s是由断层面的滑动分量组成的单位方向向量，可扩展到K个震源机制。由震源机制解表示为：

由于断层滑动方向不能约束应力张量中的各项同性成分，Michael限定应力张量的迹为零[18]：

于是，应力分量t只有5个未知分量：

最后，可以采用L2范数的广义线性反演[30]求解公式(2)，得到：

在震源机制确定的两个节面中，只有一个是真实的断层面，另一个是辅助断层面，真实断层面稳定性更差因而更容易受到剪切破裂的影响[31]。摩尔-库伦破裂准则表示，只有当节面上的剪切应力超过临界值时断层才能被激活，根据这一准则可以对发生破裂的可能性进行量化。断层面上的剪切应力与临界值的差值越大则越不稳定，也就越容易被激活，这个断层面即为真实的断层面。Vavryčuk提出一个参数I来量化断层的不稳定性[25]：

I的取值范围从0(最稳定)到1(最不稳定)。τc和σc分别为最优断层面上的剪切应力和有效正应力；τ和σ分别为所分析断层面上的剪切应力和有效正应力。由于式(9)与绝对应力值无关，所以不稳定性I是一个相对值。选取不稳定性I值较大的节面作为真实断层面后，再结合上述Michael的线性反演方法进行迭代，直至得到最优的应力模型。完整的应力反演过程如图1所示。

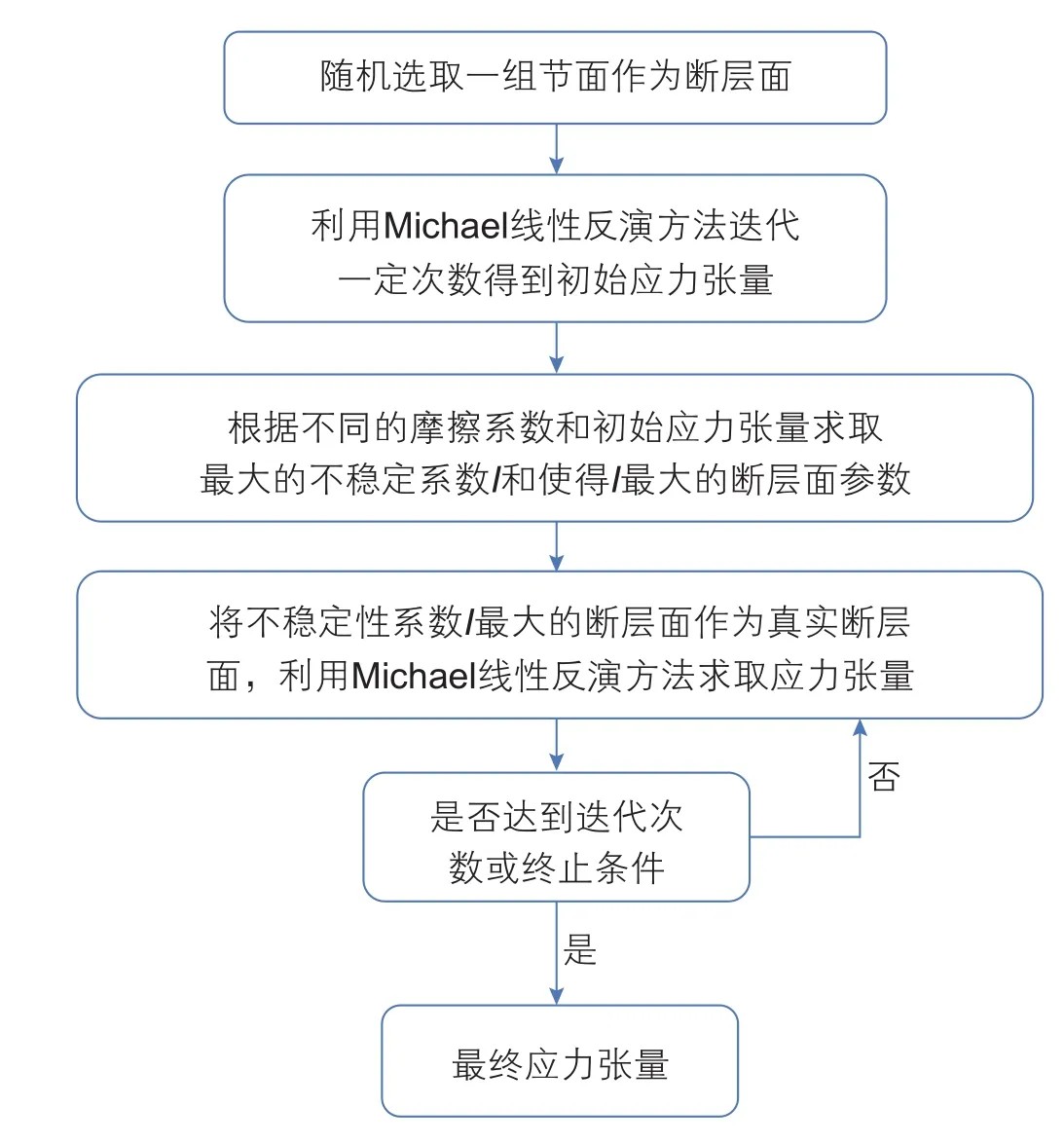
图1 迭代联合应力反演流程图Fig. 1 Flow chart of iterative joint inversion for stress

3 合成数据分析

为了确定应力场的复杂性对应力反演结果的影响，我们设计了两组数值实验。第一组实验以单一类型的应力模型作为“真实”的应力场，选取对应的震源机制作为观测资料，并加入不同的噪声水平，分析其对应力反演的影响；第二组实验选取了多种类型的应力模型对应的震源机制，给定相同的噪声水平，用以观测应力场的不均匀性对应力反演的影响。由于水力压裂过程中张裂隙的能量远小于剪切破裂的能量，在波形记录中很难观测到张裂隙产生的地震波[20]，所以本文在研究过程中选取的震源机制都是DC类型的。

3.1 均一应力场

在这一组数值实验中我们选取了正断层震源机制对应的应力模型作为“真实”应力场，应力主轴 的 方 向 分 别 为σ1=(45°，90°)，σ2=(225°，0°)，σ3=(315°，0°)(方位角和倾角)，对应的断层面解为(45°，45°，270°)(走向、倾角和滑动角)，如图 2所示。震源球中(左图)白色区域(P轴)对应压应力方向，红色区域(T轴)对应拉应力方向。极坐标投影图(图2b)中绿色圆圈、叉号和十字依次表示最大主应力σ1、中间主应力σ2和最小主应力σ3的方向，切向代表应力轴的方位角(0°～360°)，径向代表应力轴的倾角(0°～90°)，投影点与圆心的距离越大对应的倾角越小，投影点落在圆周上对应倾角为0°，投影点落在圆心处对应倾角为90°。图中清晰可见应力模型的三个主应力轴的方向依次对应主压应力轴(P轴)、零轴(B轴)和主拉应力轴(T轴)的方向。震源机制由归一化的偏应力张量求取，因此，不需要应力值的绝对大小。由于在实际反演应力场的过程中所使用的震源机制资料总是具有一定的不确定性，我们将这种不确定性视为噪声。

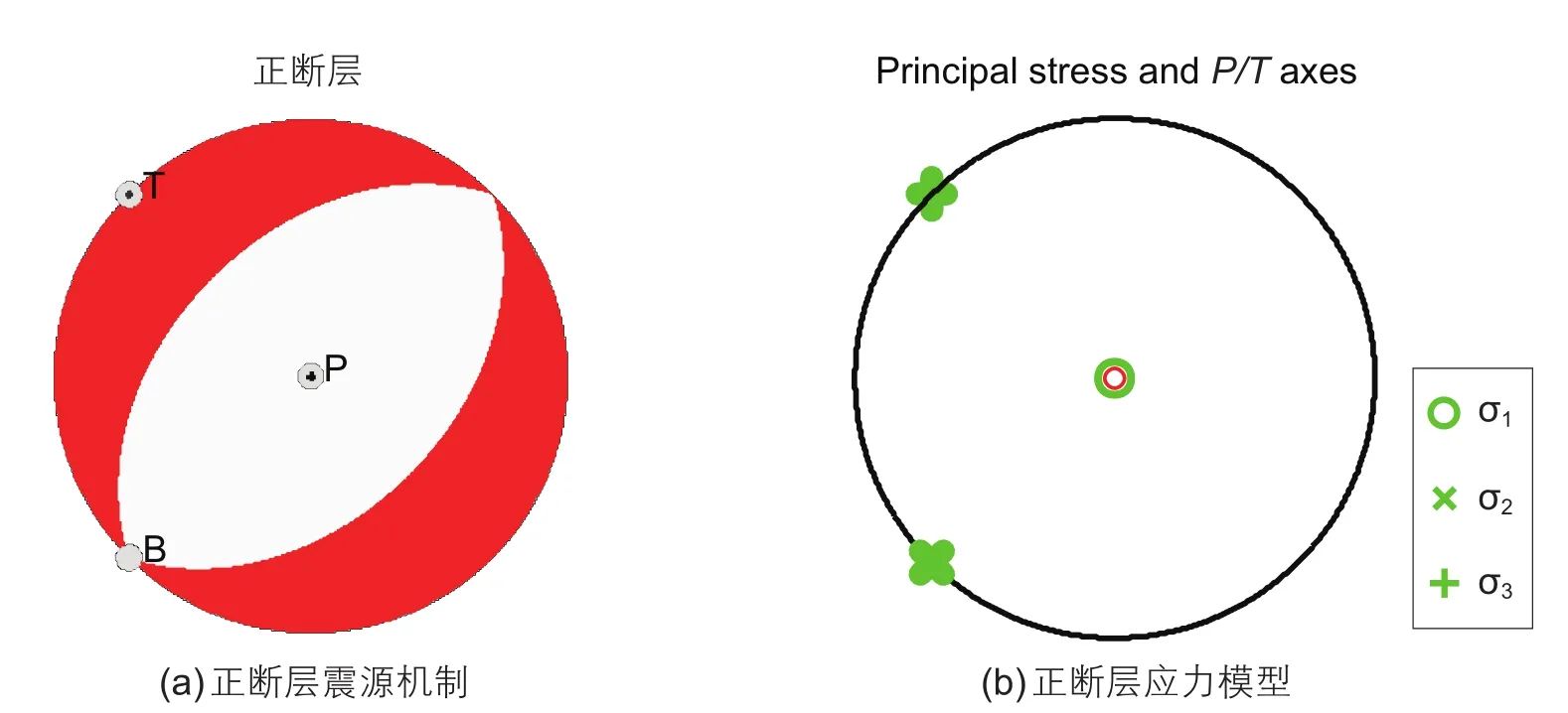
图2 正断层震源机制及对应的应力模型Fig. 2 Focal mechanism a of normal fault and corresponding stress model b

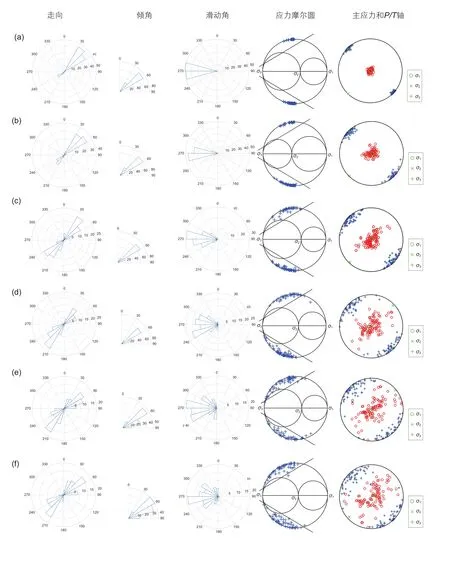
图3 不同噪声水平的震源机制对应的断层面解的分布情况及应力反演结果图，(a)～(f)对应噪声水平分别为5°，10°，20°，30°，40°和 50°Fig. 3 Distribution of fault plane solutions and stress inversion results of corresponding focal mechanisms with different noise level of 5°, 10°, 20°, 30°, 40° and 50°(a-f)

在本组数值实验中，我们将这种噪声表示为观测资料的断层面法向与“真实”震源机制的断层面法向之间的夹角，考察的随机噪声水平最大值分别为5°，10°，20°，30°，40°和 50°，这分别对应了添加噪声之后的断层面法向与“真实”的断层面法向之间夹角的最大值。在本次实验中选取的观测资料数目为100，在不同的噪声水平下使用相同的反演参数求解对应的应力模型。

图3给出了加入不同水平的噪声后观测资料的断层面解的分布情况以及应力反演结果，a～f依次对应了最大噪声水平分别为 5°，10°，20°，30°，40°和 50°的情况。其中前3列分别是断层面的走向、倾向和倾角的玫瑰花图，图中清晰可见走向围绕在45°左右扰动，倾角围绕在45°左右扰动，滑动角围绕在270°左右扰动，并且随着噪声水平的增加断层面解的扰动也逐步增大。我们选取的断层面解都满足摩尔—库伦破裂准则[32]：

其中τ和σn分别为断层面的剪切应力和正应力；S0为岩石的内聚力；µ为摩擦系数；P为岩石的孔隙压力。本文中我们取岩石内聚力S0为0.2[33]，将孔隙压力P看作0，由于应力反演过程中对摩擦系数并不敏感，所以我们给定摩擦系数µ为0.6[26]。在图2第4列的应力摩尔圆中，蓝色十字代表各个断层面上剪切应力与正应力的对应关系，可以看出基本所有的十字都落在破裂线之外，说明我们选取的断层面上剪切应力都大于岩石内聚力和有效正应力共同形成的阻力，满足摩尔-库伦破裂准则。

图3中第五列为Vavryčuk的迭代联合反演方法[25-26]得到的应力反演结果，用极坐标的下半球投影展示，图中红色圆圈表示P轴的投影分布，蓝色十字表示T轴的投影分布。图中的P轴和T轴的方向均随着噪声水平的增大而变得离散，与断层面解的玫瑰花图相对应，但是仅凭肉眼无法分辨出主应力轴方向的细微偏差。反演结果的误差如表1和图4所示，滑动误差表示反演得到的剪切应力方向与所有断层面上的滑动方向之间夹角的平均值；滑动标准差表示上述夹角的标准差；应力轴误差表示反演得到的3个主应力轴与对应的“真实”应力轴之间的夹角，应力方向误差表示应力轴误差的平均值。由于根据震源机制求解应力场的一个重要假设就是断层沿分解的剪切应力方向滑动，所以我们用滑动方向与剪切应力的偏差来衡量反演结果的可靠性。从表1和图4中可以看出滑动误差和滑动标准差均随着震源机制噪声水平的增加而变大，并且滑动方向的误差对噪声水平的敏感性相较应力方向对噪声水平的敏感性要大得多。图4b的柱状图更直观的表示出反演得到的应力方向的误差随噪声水平的增加整体呈上升趋势，但是无论哪种噪声水平情况下反演得到的应力主轴与“真实”的应力主轴差别不大，所有应力主轴的偏差都不超过8°，这一点从图3第5列的应力反演结果图中也得以验证。这说明在均一应力场的情况下，噪声水平的大小即震源机制的不确定性对于求解应力模型的影响不大，但是会对滑动方向的误差统计带来一定程度的影响。

表1 不同噪声水平下应力反演结果的误差值Table 1 Errors of stress inversion results with different noise

3.2 复杂应力场

为了得到观测应力场的不均匀性对应力反演的影响，我们在第二组数值实验中构建了多种类型的应力模型共同作用下的复杂应力场。我们仍然以第一组实验中的正断层震源机制对应的应力模型为主，观测资料数目所占比例始终不小于50%。在观测资料中依次加入左旋斜滑正断层、右旋斜滑正断层、走滑断层、逆断层、右旋斜滑逆断层和左旋斜滑逆断层的不同震源机制类型所对应的应力模型，即构成复杂应力场的震源机制类型从2种累计到7种，除正断层外，其余各震源机制类型占相同比重。不同震源机制类型对应的应力模型和断层面解如表2所示。本组实验中的观测资料数目仍为100，震源机制的不确定性均采用10°的随机噪声误差。以包含的震源机制类型数目表示应力场的不均匀程度，使用相同的反演方法和相同的参数反演应力状态。

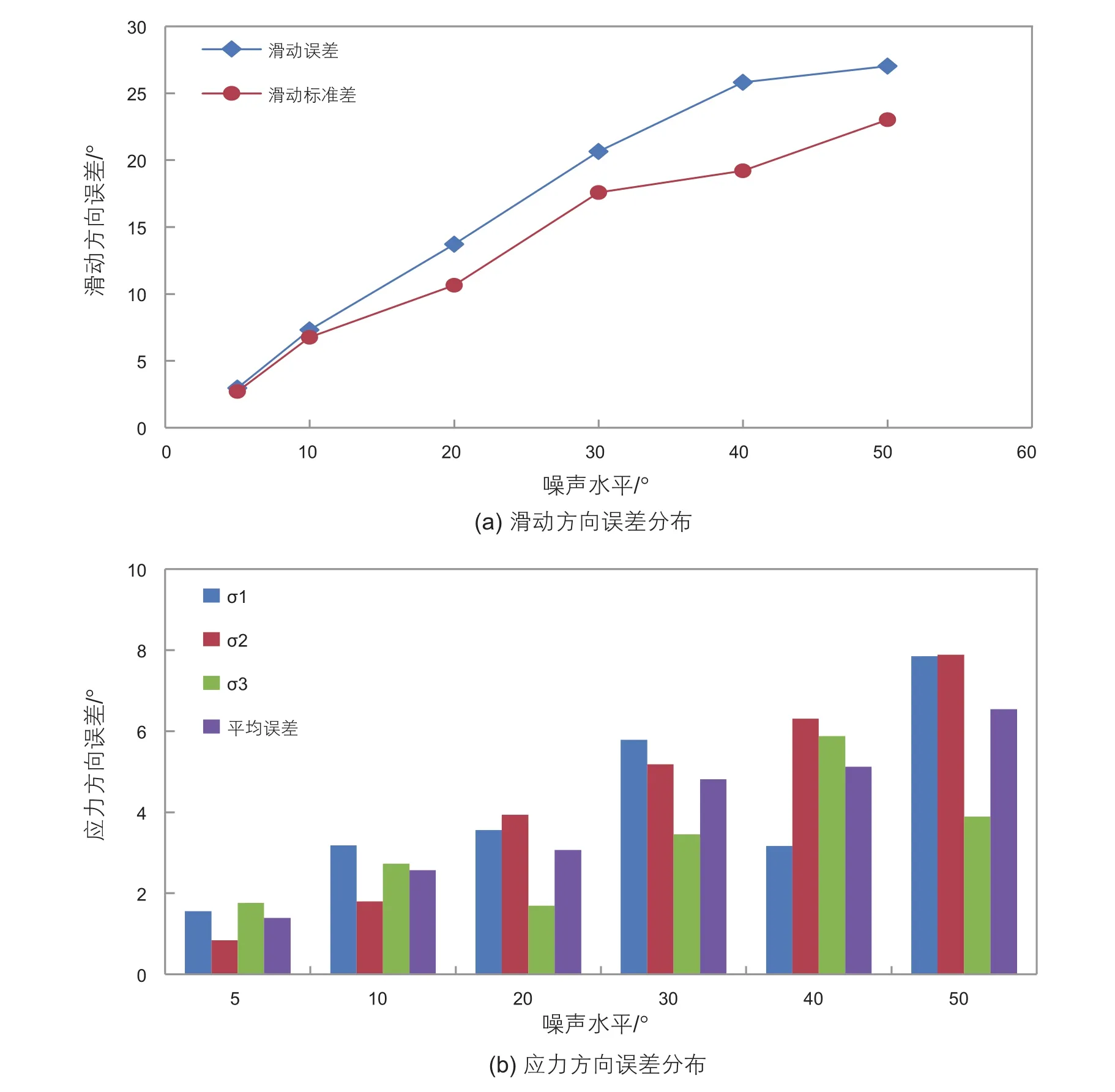
图4 不同噪声水平情况下应力反演结果误差分布Fig. 4 Errors distribution of stress inversion results with different noise, (a) distribution of slip deviation; (b) distribution of stress direction error

表2 不同震源机制类型对应的应力模型和断层面解Table 2 Stress models and fault plane solutions of different focal mechanisms

图5 不同复杂程度的应力场对应的断层面解的分布情况及应力反演结果图，(a)～ (f)对应复杂程度分别为2～7Fig. 5 Distribution of fault plane solutions and stress inversion results of corresponding stress fields with different complexity of 2～7 (a～f)

图5展示的是观测资料中依次加入不同类型的震源机制进行应力反演对应的断层面解的分布情况和应力反演结果，a～f依次对应了震源机制类型数目分别为2～7种的情况。从前3列的玫瑰画图可以看出，断层面解的走向、倾向和滑动角的分布随着应力场复杂程度的增加均呈现出逐渐分散的趋势，同时第5列应力反演结果图对应的P轴和T轴方向分布也逐渐变得离散。值得注意的是，图5d～f的应力摩尔圆中可以看出，当加入逆断层、右旋和左旋斜滑逆断层3种类型的震源机制后，有相当一部分蓝色十字并没有落在破裂线之外，即这些点对应的断层面上剪切应力与正应力的关系不满足摩尔-库伦破裂准则。这说明当观测应力场的复杂程度较高时，直接反演得到的单一应力模型不可能符合观测资料中所有的断层类型，一些断层面在这样的应力状态下无法满足破裂条件，这种情况下的应力反演结果存在较大的误差。不同复杂程度的应力状态下反演得到的应力模型如图5第5列所示，虽然加入了多种类型的震源机制，但是在以正断层类型占主要成分的条件下，反演得到的结果则更趋于正断层对应的应力模型。此外，图中d～f由于较多的断层面解不符合破裂条件，所以应力反演的结果在正断层类型所占比例不变的情况下出现了较大的偏差，更说明了在复杂应力状态下反演单一应力模型的不可靠性。

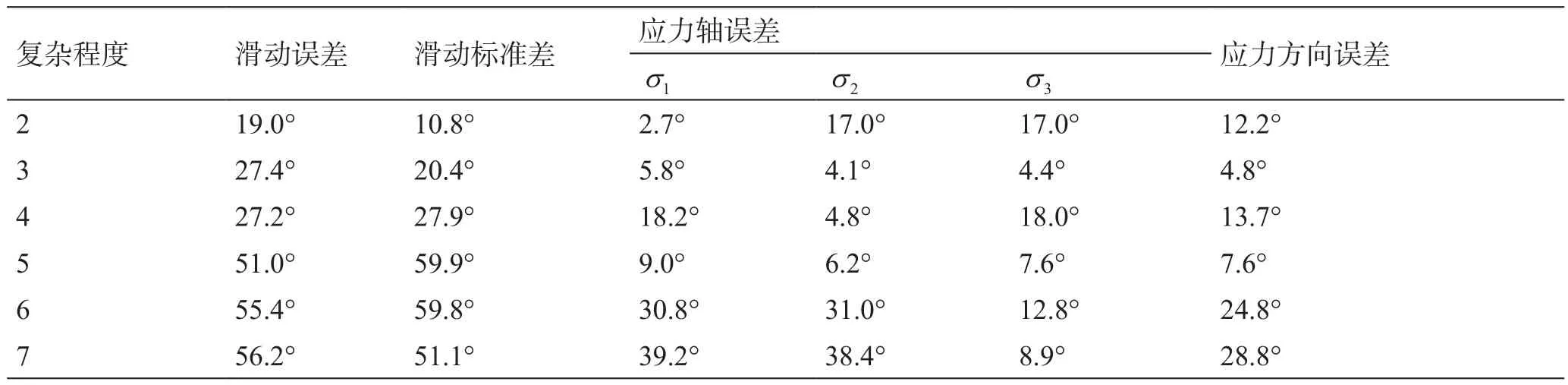
表3 不同复杂程度的应力场中应力反演结果的误差值Table 3 Errors of stress inversion results in corresponding stress fields with different complexity

图6 不同复杂程度的应力场中应力反演结果误差分布Fig. 6 Errors distribution of stress inversion results in corresponding stress fields with different complexity, (a) distribution of slip deviation; (b) distribution of stress direction error

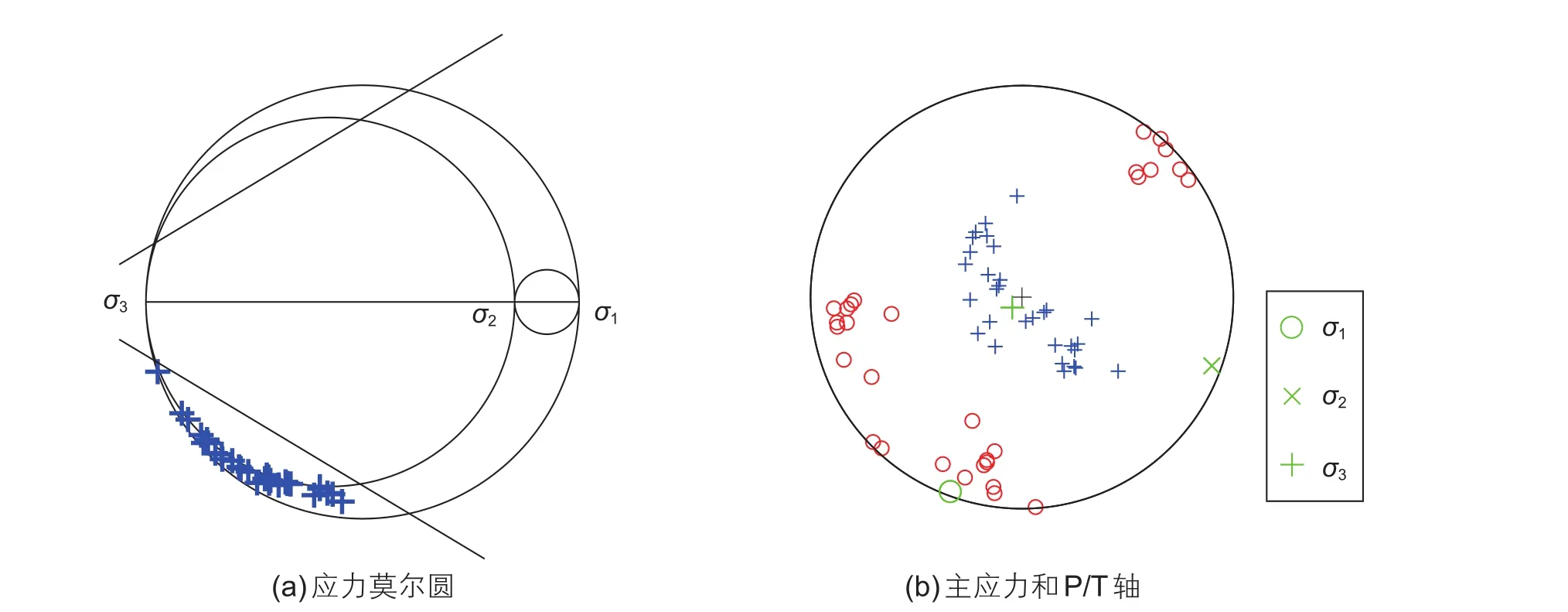
图7 逆断层、右旋斜滑逆断层和左旋斜滑逆断层对应的三种震源机制构成的观测资料进行应力反演的结果Fig. 7 Stress inversion result from focal mechanisms constituted of reverse fault, reverse right-lateral oblique fault and reverse left-lateral oblique fault, (a) Mohr circle diagram, (b) Principal stress and P/T axes

图8 正断层和逆断层对应的两种震源机制构成的观测资料进行应力反演的结果Fig. 8 Stress inversion result from focal mechanisms constituted of normal fault and reverse fault, (a) Mohr circle diagram, (b)Principal stress and P/T axes

表3和图6给出了随着应力场不均匀性的增大应力反演结果的误差值。从图6a可以更直观的看出随着应力场的复杂程度增加即观测资料的震源机制类型增多，滑动误差和滑动标准差的值均呈上升水平，并且通过对比图4a可以发现，滑动方向的误差值明显较高，这说明与震源机制的不确定性对滑动方向误差产生的影响相比，应力场的复杂程度产生的影响要大得多。值得注意的是当震源机制类型数目增加到5时，滑动方向的误差值有一个明显的陡增，这一显著变化也对应了图5d-f反演结果的不可靠性。另一方面，当应力场的不均匀程度变化时，应力主轴的误差变化(表3和图6b)并没有明显的规律性，这可能是由于我们用于对比的应力模型是占比为50%的正断层对应的应力模型，本身就具有一定的不确定性，所以这种情况下以此来衡量应力主轴的误差值并不可靠。由此可见，在复杂程度较高的应力条件下，应力反演的滑动方向误差要比应力主轴的误差更能反映出反演得到的应力模型对所有断层面的适用性。

此外，为了探究较大的反演结果误差是否由于最后加入的3种类型的震源机制(逆断层、右旋斜滑逆断层和左旋斜滑逆断层)本身造成的，我们将它们单独作为观测资料进行应力反演。得到的反演结果如图7所示，从应力摩尔圆(图7a)中可以看出，获取的应力模型使得所有的断层面都满足摩尔-库伦破裂条件，反演得到的应力模型滑动方向误差平均值为32.4°，标准差为20.9°，误差值的大小与表3中只有3种类型震源机制条件下反演结果的误差值相差不大。说明震源机制类型的数目大于5时较大的反演误差确实是由于应力场的复杂性较高造成的，这也进一步证明了在较为复杂的应力场条件下，反演求解单一的应力模型是不可靠的。

由于观测资料中加入的前两种类型的震源机制分别是左旋斜滑正断层和右旋斜滑正断层(图5a、5b)，这两种断层类型都是以正断层为主，同时伴随有走滑分量，与正断层的震源机制具有一定的相似性，所以在与正断层一起进行应力反演时可能引起的反演结果中误差值相对较小，反演得到的应力模型也可以使得所有断层面都满足破裂准则。作为对比，如果我们在一开始就加入逆断层对应的震源机制，在已知有正断层和逆断层两种类型的应力条件下使用相同的参数进行反演，那么，得到的应力模型滑动方向误差平均值为19.7°，标准差为13.6°，与表3中对应的两种类型条件下误差大小处于相同水平。但是从反演得到的应力摩尔圆(图8a)中能够发现有大约一半的断层面处于破裂线以内，不满足破裂条件。并且反演得到的应力模型(图8b)与逆断层对应的应力条件是一致的，而此时观测资料中以正断层为主，所以这样的反演结果并不可靠。虽然此时观测资料中仅仅只有两种类型的震源机制，但是正断层和逆断层两种类型的震源机制差异较大，所对应的应力场更是大相径庭，那么同时存在这两种震源类型的应力场也是较为复杂的，求取单一模型的应力反演方法在这种情况下并不适用。

图9 微地震监测实际数据的断层面解分布及应力反演结果。(a)大庆油田压裂数据；(b)长宁区块压裂数据Fig. 9 Distribution of fault plane solutions and stress inversion results of real fracturing data in microseismic monitoring. (a)data in Daqing oil field, (b) data in Changning block

4 实际数据分析

为了检验数值实验得到的结论，我们选择了具有上述合成数据特征的两组微地震监测实际数据来进行测试。图9a对应了大庆油田某井的部分水力压裂事件，从走向、倾角和滑动角的玫瑰花图可以看出震源机制的断层面解相似程度较高，均一性较好，这些断层面的走向大多沿着北偏西20°左右，倾角集中在60°～90°的范围，而滑动角大多接近270°，接近正断层类型。我们同样利用Vavryčuk的迭代联合反演方法[25-26]对这组实际数据进行应力反演，所有断层面的P/T轴方向及反演得到的应力主轴方向如图所示，σ1=(242.2°，79.9°)，σ2=(332.6°，0.1°)，σ3=(62.7°，10.1°) (方位角和倾角)，近似正断层对应的应力状态，应力摩尔圆显示几乎所有断层面对应的应力关系都满足该应力状态下的摩尔-库伦破裂准则。反演结果对应的滑动误差为23.2°，滑动标准差为24.4°，与表1和表3的误差值对比，可以看出应力反演的结果是可靠的，误差值可能是由于应力场具有一定的不均匀性或者数据本身的误差值造成的。

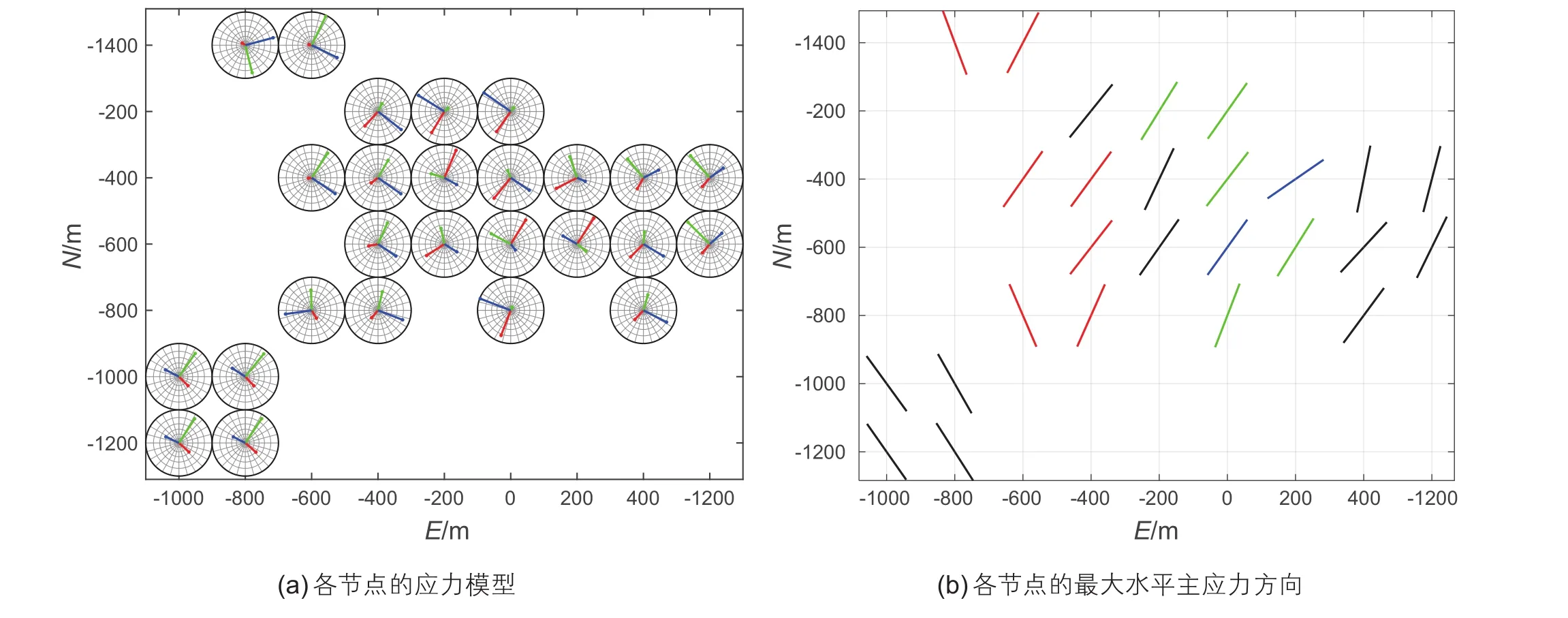
图10 阻尼区域应力反演结果Fig. 10 Results of damped regional-scale stress inversion. (a) Stress models at every grid node; (b) direction of the maximum horizontal principal stress at every grid node

图9b对应长宁区块某井的部分压裂事件，断层面的走向、倾角和滑动角的玫瑰花图分布较为离散，说明震源机制的差异性较大，非均匀性水平较高，从断层面的P/T轴方向分布也可以看出震源机制类型较为复杂。反演得到的应力主轴方向如图中绿色标志所示，σ1=(40.3°，16.7°)，σ2=(161.8°，60.2°)，σ3=(302.7°，23.9°)(方位角和倾角)，显而易见，反演得到的应力模型无法契合大部分震源机制对应的断层面，并且从应力摩尔圆的分布图也可以看出相当一部分的断层面在该应力状态下无法到达破裂条件，所以反演结果的误差值较高，滑动误差为54.3°，滑动标准差为49.9°。可见，应力场的非均匀程度对应力反演的影响很大。为了优化该区域的应力反演结果，我们又利用Hardebeck的阻尼区域应力反演方法[28]对这一组水力压裂事件进行试算。为了降低随机选取真实断层面而导致的误差，我们先通过计算断层面的不稳定性I[25-26]，选取I值较大的节面作为真实断层面，之后将研究区域以200m为间隔进行网格划分，不同的事件按位置划归到距离最近的节点，得到26个包含事件的有效节点，并在相邻节点之间加阻尼因子，通过计算选取最优的阻尼因子为1.1。对所有节点同时进行阻尼应力反演，最终得到各个节点的应力模型如图10a所示，图中红色、绿色和蓝色线段分别表示σ1、σ2和σ3的方位角和倾角在极坐标下的投影，可以看出各个节点的应力状态都不尽相同。不过由于相邻节点之间有阻尼因子进行约束，所以相邻节点反演得到的应力方向差异较小，不易出现较大的突变。

图10b给出了各个节点处最大水平主应力的方向，可以看出最大水平主应力大多呈NE或N-NE方向分布，西南区域的最大水平主应力转为沿N-NW方向。其中红色代表正断层类型，绿色代表走滑断层类型，蓝色代表逆断层类型，黑色代表斜滑断层类型，表明了该区域应力场的复杂程度较高。反演结果的滑动误差为46.1°，滑动标准差为45.0°，与直接反演结果的滑动方向误差值相比有一定程度的降低，但是误差值依然较大，可能与网格划分有一定的关系。对于如何解决该复杂区域应力状态的反演问题，我们在另一部分研究工作[34]中进行了深入探讨，有效改善了应力反演的效果。

5 结论

在水力压裂微地震监测中，对于裂缝尺度较小并且应力场较为复杂的情况下，如果只是反演得到单一应力模型往往误差较大。本文通过两组数值实验，以Vavryčuk的迭代联合反演方法为基础，分析了应力场的不均匀水平对应力反演结果的影响。

第一组实验的观测资料只包含一种类型的震源机制，即“真实”应力场是均一的简单应力场的条件下，随着观测资料中的噪声水平不断提高，应力方向和滑动方向的误差均随观测资料的噪声水平增大而增大。但是应力主轴方向的偏差始终很小，而滑动方向的误差对噪声水平的增加却敏感的多。这表明在均一应力场的作用下，噪声水平的大小即震源机制的不确定性对应力反演结果的准确性影响较小，但是会影响滑动方向的误差大小。

第二组数值实验中构建了多种类型的应力模型共同作用下的复杂应力场。随着观测资料中构成复杂应力场的震源机制类型从2种累计到7种，应力场的复杂程度相应增加，滑动方向的误差值显著增大，并且远大于震源机制的不确定性造成的误差值。另外，应力场的复杂程度较高会导致反演得到的单一应力模型不可靠，部分断层面无法满足破裂条件。这些结果都证明了求取单一模型的应力反演方法在复杂应力场条件下并不适用。在第二组数值实验中应力场不均匀程度的变化对应力主轴的误差却没有规律性的影响，而滑动方向的误差则更能反映出反演结果的可靠性。

两组实际数据的反演结果验证了上述结论。大庆油田某井的部分水力压裂事件震源机制的断层面解相似程度较高，均一性较好，反演得到的单一应力模型能够较好的适用于绝大多数断层面特征。而长宁区块某井的部分压裂事件由于震源机制的差异性较大，非均匀性水平较高，使得反演得到的应力模型无法契合大部分震源机制对应的断层面，相当一部分的断层面在该应力状态下无法到达破裂条件。由此可见，应力场的非均匀程度对应力反演的影响很大。

致谢

本文在研究过程中得到了东方地球物理公司的微地震监测实际数据支持，在此表示感谢。