关于正项级数几个习题的联系与推广
2023-02-07 01:21华梦霞
南阳师范学院学报 2023年1期
陈 庆, 华梦霞
(南阳师范学院 数学与统计学院,河南 南阳 473061)
做好习题是使学生了解数学思想方法和精神实质的有效途径之一.在教学中若能引导学生发现不同习题之间的联系,进而联系不同章节之间的学习内容,将有助于进一步加深学生对知识的理解,培养其发散思维.本文将对数项级数的两个习题进行联系,同时给出其在无穷积分情况下的表现形式.
文献[1]第169页例3.2.1,文献[2]第26页总练习题分别给出了如下习题:
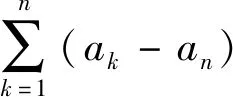


命题1{an}单调递减趋于0, 则

证明:“⟸” 即为习题1.






若仅知{an}单调递减,不知{an}是否收敛于0,可将命题1结论改写为如下形式.
命题2{an}单调递减,则以下论述等价:



(2)⟹(1) 由{an}单调递减,得{a1-an}单调递增.



数项级数和无穷积分之间存在着密切的联系,利用一般测度的积分,许多时候可将积分与级数统一处理[3-5]. 因此在数项级数、无穷积分中有许多相联系、相对应的知识模块或结论. 这在习题中往往也有体现.在教学中,如果能有意识地加强此方面的引导,将有助于学生理解数项级数和无穷积分之间的联系,同时为更好地学习实变函数、泛函分析等后继课程,从不同课程知识更深地理解部分习题打下基础[6].
如文献[7]第282页有如下习题:


显然习题2与习题3极为相似, 在教学中,可以引导学生思考:既然习题2与习题3关系密切,那么在处理无穷积分敛散性时,能否得到与命题1、命题2类似的结果,并适时地向学生介绍如下结果.






于是对∀N>u,


命题4f(x)在[a,+∞)上单调递减,则以下论述等价:




(2)⟹(1)f(x)在[a,+∞)上单调递减,∃M>0,当u>a+1时,
即

所以

又x∈[a,a+1],有f(x)≥f(a+1),从而



猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
数学物理学报(2022年1期)2022-03-16
新世纪智能(数学备考)(2021年11期)2021-03-08
新世纪智能(数学备考)(2020年11期)2021-01-04
中学生数理化·高一版(2019年9期)2019-10-12
数学年刊A辑(中文版)(2018年1期)2019-01-08
中文信息(2017年12期)2018-01-27
山西大同大学学报(自然科学版)(2016年6期)2016-01-30
中央民族大学学报(自然科学版)(2015年2期)2015-06-09

