超疏水锯齿表面振动液滴的动态特性

黄宝罗，贾志海，康学良，潘桂暖

超疏水锯齿表面振动液滴的动态特性

黄宝罗，贾志海，康学良，潘桂暖

（上海理工大学，上海 200093）

在振动的超疏水锯齿表面上，液滴表现出明显的运动特征，探究在该过程中液滴的运动机理及影响因素。采用铝片制作一系列具有一定倾角和高度的非对称锯齿状表面，使用疏水涂层Glaco Soft 99均匀喷涂，并干燥其表面，重复多次实验，直到表面具有稳定的超疏水性。加载一定的振动，对表面振动液滴的动态行为进行研究。在一定的振动范围内，当频率的作用范围为10～100 Hz，振幅的作用范围为0～2 mm时，随着振动参数的增加，超疏水锯齿表面上的液滴会产生4种不同的行为，即静止、定向蠕动、跳跃、破裂等。实验表明，超疏水锯齿表面振动液滴的最快运动速度为8 cm/s。针对液滴的定向蠕动行为，运用力学分析方法，建立了液滴运动的物理模型，并分析了振动特征参数、锯齿表面参数、液滴体积对液滴运动特征的影响。对于一定尺寸的液滴，存在一个由共振频率和最优振幅组成的最佳的振动加速度，可使液滴达到该条件下的最优运动速度。同时，通过改变锯齿表面的结构参数，可使液滴运动速度更快，并且随着液滴体积的增加，液滴运动速度呈现先增快、后减慢的趋势。

液滴；超疏水；锯齿表面；振动；定向驱动

操控液滴运动在强化换热[1]、抑制结冰[2]、液体运输[3]等领域有着广阔的应用前景。从Linke等[4]利用不对称锯齿状表面首先实现了液滴定向运动以来，采用非对称表面操控液滴运动成为了重要的研究方向。研究者对这种非对称表面进行了大量的研究，认为液滴在这种非对称表面上形成的非对称力是促使其运动的根本原因。

近年来，基于非对称表面结构的研究得到了广泛的关注，许多不同形式的表面结构被设计出来，如径向辐射式表面[5-6]、微脊状疏水表面[7-8]、楔形梯度表面[9-10]等。研究者通过不断改变表面结构拓扑形式，对液滴在各种不同表面的行为特征、运动机理等进行了探讨。由于这种非对称表面结构的驱动力较微弱，液滴的运动速度较缓慢[11]，移动的距离也非常有限[12]，有时甚至只有几毫米，因此采用外界刺激强化液滴的运动速度成为目前常用的方法，如温度场[13]、电场[14]、磁场[15]、光照[16-17]等。近年来，机械振动方法也被引入操控液滴运动的研究中，一些研究者采用振动方法研究了液滴的浸润状态转变特征[18-19]，认为振动特征参数显著影响着液滴的浸润状态转变过程。然而，采用振动诱导液滴运动的研究还不多见[5,20]，在振动作用下液滴的运动机理及振动特征参数对液滴运动的影响还不清楚。探究在振动条件下，如何操控液滴成为重点研究方向，该技术的发展也为解决一些常见工业难题提供了新的思路。例如，冷凝器的冷凝换热过程往往伴随着膜状凝结现象的产生，这是工业领域常见的一大难题。水膜的产生大大增加了表面热阻，从而降低了传热性能。这类问题在动力、能源、化工、电力等实际工程应用中仍普遍存在，目前还无较好的解决方法，文中利用振动的液滴操控技术有望实现凝结水膜的破裂和快速输送，提高设备的传热性能。

文中采用铝片制作不同结构参数的非对称锯齿表面，探讨通过机械振动对锯齿表面液滴的动态行为，建立液滴运动的物理模型，分析振动特征参数、锯齿表面特征参数、液滴尺寸对液滴运动特征的影响。文中研究将为后续采用机械振动操控液滴运动提供理论支持。

1 实验表面和装置

实验使用的锯齿表面由线切割工艺加工制作，通过改变齿高和锯齿倾角来改变锯齿的表面参数。使用疏水涂层Glaco Soft 99均匀喷涂锯齿表面，然后置于90 ℃环境下烘干，重复多次实验，使锯齿表面具有稳定的超疏水性，如图1a所示。利用接触角测量仪测量锯齿表面的液滴表观接触角，介质采用去离子水。

实验装置如图1b所示，首先将锯齿表面置于振动台上，使用微量进样器在锯齿表面沉积1滴液滴。将振动台产生的垂直振动作为振动源，利用信号发生器和功率放大器对振动源输出的振动频率和振幅进行控制。实验台使用的振动频率为10～100 Hz，振幅为0～2 mm。依次打开信号发生器和功率放大器控制振动的频率和振幅。利用高速摄影仪（Fastec Imaging Hispec 3），以1 000帧/s的频率来捕捉液滴的动态特征。

图1 实验表面和装置

2 结果与讨论

2.1 振动液滴的动态行为

将1滴80 μL的去离子水液滴轻轻沉积在=30°、=1.2 mm的锯齿表面，对锯齿表面加载一定的振动，=40 Hz，振幅分别取0.3、0.4、1.2、2 mm。随着振幅的变化，液滴会依次表现出静止、定向蠕动、跳跃、破裂等行为。当振动台提供的能量较小时，不足以克服液滴的重力和运动阻力，液滴在原地不动，只在垂直方向伸缩，将此时的液滴状态称为静止状态，如图2a所示。当振动的能量达到某一阈值时，液滴开始稳定地沿着锯齿直角边方向做定向运动，此时液滴不会脱离表面，而是在表面蠕动，将此时的液滴状态称为定向蠕动行为，如图2b所示。随着振动能量继续增加，液滴逐渐在运动过程中与表面脱离，液滴弹跳着向前运动，如图2c所示，将此时的液滴状态称为跳跃行为。当振动能量进一步增加，液滴形变剧烈且极不稳定地运动，并伴随着液滴破裂现象的发生，如图2d，将此时的液滴运动状态称为破裂行为。

2.2 力学分析

选择定向蠕动行为作为研究对象，分析液滴运动的机理。在振动作用下，液滴会侵入锯齿沟槽，如图3所示，导致液滴两端的动态接触角发生了变化，并在三相接触线上产生了非对称作用力。在该作用力的作用下，液滴产生向锯齿直角边的定向运动（定义为正方向）。将运动过程中液滴前进端动态接触角定义为前进角A，另一端定义为后退角R。

液滴在运动过程中产生的驱动力D的计算见式（1）。

图2 振动液滴在同一块锯齿表面（β=30°，h=1.2 mm）的静止、定向蠕动、跳跃、破裂行为

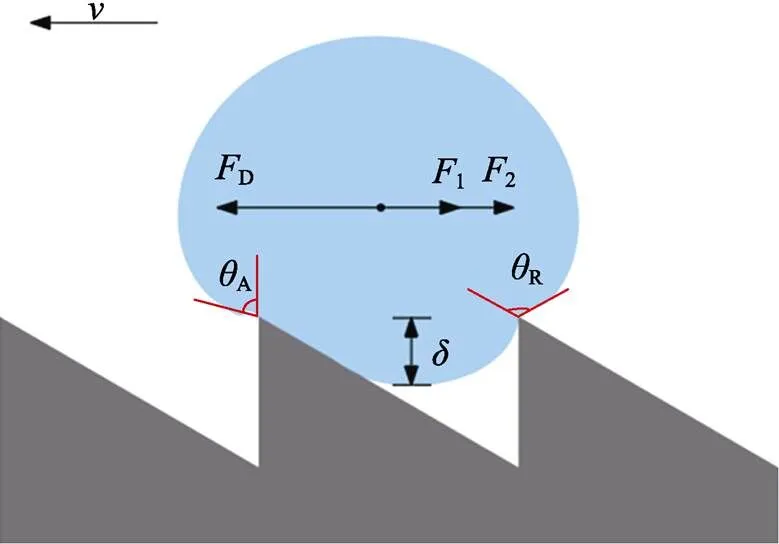
图3 液滴在锯齿表面上运动时的受力分析

式中：为取决于接触线形状的系数，由实验确定；为液滴宽度；L为液体的表面张力；A为前进角，R为后退角。

在驱动力D的作用下，液滴沿着锯齿表面开始运动，在一定时间内，液滴质心在水平方向的位移距离为D，则驱动力做功D，见式（2）。

液滴在锯齿表面运动时，在水平方向会受到阻力，当液滴移动D时，阻力做功，见式（3）。

这里f包含2个部分。根据文献[21]，液滴在运动过程中与锯齿产生碰撞，导致部分动能损失，引起这部分动能损失的力的计算见式（4）。

由于振动液滴会侵入沟槽内部，在运动过程中还需克服一定的势能障碍，这部分能量损失对应的力的计算见式（5）。

液滴受到的总阻力f的计算见式（6）。

式中：1、2为系数，主要取决于锯齿表面的结构尺寸；为液滴侵入的深度；为液滴密度；为液滴半径；为液滴速度；为重力加速度；为锯齿底边长。

液滴在运动过程中的动能增量D计算见式（7）。

液滴在运动过程中，驱动力做功D转换为阻力做功f及动能增量D，见式（8）。

液滴运动速度的计算见式（9）。

式中：1为某时刻由实验测得的真实速度；2为时间间隔后的理论速度，它与实际速度的比较如图4a所示。

选取时间步长为10 ms，采用液滴质心在水平方向的运动速度代替液滴整体的运动速度。将10 ms中液滴质心在水平方向的位移距离定为D。理论速度与实验测得的实际速度的比较如图4所示。从图4a中发现，随着时间的变化，速度曲线呈现较大的波动。这是因为液滴在运动过程中会发生波动，即在振动的作用下存在铺展和收缩的过程。同时，液滴在运动过程中处于锯齿的不同位置，导致前进角和后退角不断变化，甚至出现前进角大于后退角的情况，从而出现瞬间的驱动力方向与运动方向相反的情况，但在惯性的作用下，液滴依旧保持原方向运动。在两者的共同作用下，造成速度曲线出现较大的波动。需要注意的是，对于时间步长的选取不宜超过20 ms，因为随着时间步长的增加，液滴在宏观上的速度趋于稳定，而驱动力依旧为瞬态值，会出现实际速度趋于平缓而理论速度依然波动较大的情况。对不同锯齿表面液滴的理论速度与实际速度进行了比较，如图4b所示，液滴在水平方向的实际速度与理论速度基本一致。

图4 液滴速度对比

2.3 运动影响因素分析

2.3.1 振动参数的影响

根据文献[22]，对于具有弧状拓扑微结构的表面，依靠三相接触线产生的非对称驱动力使液滴发生运动，速度与振动的振幅和频率密切相关。根据Jung等[23]的研究，文中用2，即振动平台加速度来表征加载的振动能量，其中为振动台的振幅，为振动频率。

对于80 μL液滴，选取5种不同频率，通过调整振幅来改变振动台的加速度，获得不同振动特征下液滴的速度特征，如图5a所示。可以发现，对于不同的频率，在振动台加速度逐渐增加的过程中，液滴的运动速度会出现峰值，即液滴运动存在最优振幅，使得液滴的运动速度达到最大值。尤其是在=40 Hz时，最快速度达到8 cm/s，当超过最优振幅后，随着振幅的持续增加，液滴的运动速度逐渐减慢，且液滴的运动变得极不稳定。这是因为随着振幅的增加，振动加速度逐渐增加，振动愈加剧烈，液滴的表面波动加剧，使得驱动力中的（cosAcosR）变化复杂，即驱动力D变得不稳定。此外，随着振幅的增加，液滴侵入沟槽的平均深度变大，即平均增大，从而形成了较大的阻力，导致超过最优振幅后液滴的运动速度下降。

由图5b可知，对于不同的振幅，80 μL的液滴都在40 Hz时达到运动速度的峰值。根据Noblin等[24]的研究，液滴共振频率的计算见式（10）。

式中：为液体的密度；为液滴的振动模式数量；为液滴的表面张力；为液滴的半径。

通过计算可知，80 μL液滴对应的共振频率为40 Hz，即在液滴的共振频率下，液滴达到了最大的运动速度。经分析认为，这是因为在共振频率下振动台传递到液滴的能量传递效率最大。结合图5a可知，在共振频率下液滴达到峰值时对应的振幅最低，这为利用振动操控液滴运动振动频率的选择提供了依据。

2.3.2 液滴尺寸的影响

选用=30°、=1.2 mm的锯齿，振动频率选择液滴的共振频率，振幅采用最优振幅，即采用最佳的振动台加速度opt，分析液滴尺寸对液滴运动特征的影响，结果如图6所示。为了便于分析，采用无量纲半径R=R/λ来表征液滴的尺寸，R越大表示液滴覆盖的锯齿数越多。根据图6，发现随着R的增加，最优振动台加速度opt呈现单调递减趋势。这主要是由振动参数特性所决定，R为0.9～1.4时对应的最优振幅的变化范围为0.8～1.2 mm，但是共振频率的变化范围为70～30 Hz。因为共振频率的变化范围更广，所以对最优振动加速度opt的影响更大。对于小液滴来说，共振频率较大，所以对应的最优振动台加速度较大。随着液滴尺寸的增加，共振频率逐渐减小，且下降趋势逐渐变缓，导致曲线趋于平缓。对于较小尺寸的液滴，达到最大速度所需要的最优振动台加速度opt比大尺寸液滴大。

不同尺寸的液滴在最佳振动台加速度opt下达到的最快运动速度如图6所示。无量纲半径R在1.2附近时，即液滴体积为60 μL时，液滴的运动速度最快。这是因为当R<1.2时，随着液滴体积的增加，液滴宽度不断增加，而（cosAcosR）未发生明显的变化，导致驱动力D随着液滴的体积增加而增加，使得液滴运动速度逐渐增大。当R>1.2时，随着液滴体积的增加，液滴表面波动加剧，使得液滴宽度和（cosAcosR）在整个运动过程中变得极不稳定，导致驱动力D总体减小。其次，较大尺寸的液滴对应的阻力也较大。尤其是在液滴铺展过程中，可以填满多个锯齿沟槽，极大地增加了液滴的运动阻力，导致液滴的运动速度变慢。从实验结果来看，当R为1.2时，液滴有着较大且相对稳定的驱动力D，并且相对于大液滴，有着较小的阻力，导致此时的液滴具有较快且稳定的运动速度。

图5 振动对液滴运动速度的影响

图6 不同尺寸液滴对应的最佳振动加速度和最佳速度

2.3.3 锯齿参数的影响

为了验证锯齿表面结构参数对于液滴运动的影响，选择60 μL的液滴作为研究对象，对液滴施加的共振频率为47 Hz，选用最佳振动台加速度，使得液滴达到该条件下的最大速度。不断更换锯齿表面，获得液滴的运动速度与锯齿参数的关系，如图7所示。

由图7a可以看到，在30°的表面上，液滴的速度随着锯齿高度的增加，呈现先增大、后减小的趋势。这是因为高度较小时，（cosAcosR）较小，导致驱动力D较小，随着锯齿高度的增加，（cosAcosR）增加，在锯齿高度超过1.2 mm后，（cosAcosR）稳定。此时，由于锯齿高度较高，沟槽较深，导致嵌入沟槽的液滴体积增加，从而引起阻力的增加，导致液滴的速度降低。由图7b可知，当固定锯齿高度时，随着锯齿倾角的增加，液滴速度同样呈现先增大、后减小的趋势，其原因却不尽相同。当锯齿倾角较小时，液滴无法完全覆盖2个锯齿，液滴一端与前锯齿的尖角接触，另一端主要与后锯齿的斜边接触，产生的驱动力不足以使液滴从沟槽中排出，并越过锯齿的宽度，从而不能到达下一个锯齿，故而此时若要形成连续稳定的定向运动，对应的振动台加速度需较大。随着锯齿倾角的增加，液滴的速度逐渐增加，在达到30°后呈现下降的趋势。这是因为当倾角较大时，锯齿变得更加密集，液滴未侵入沟槽，导致液滴两端呈现的A与R基本相同，使得驱动力D接近于0。当倾角为60°时，液滴不再出现明显的运动特征。

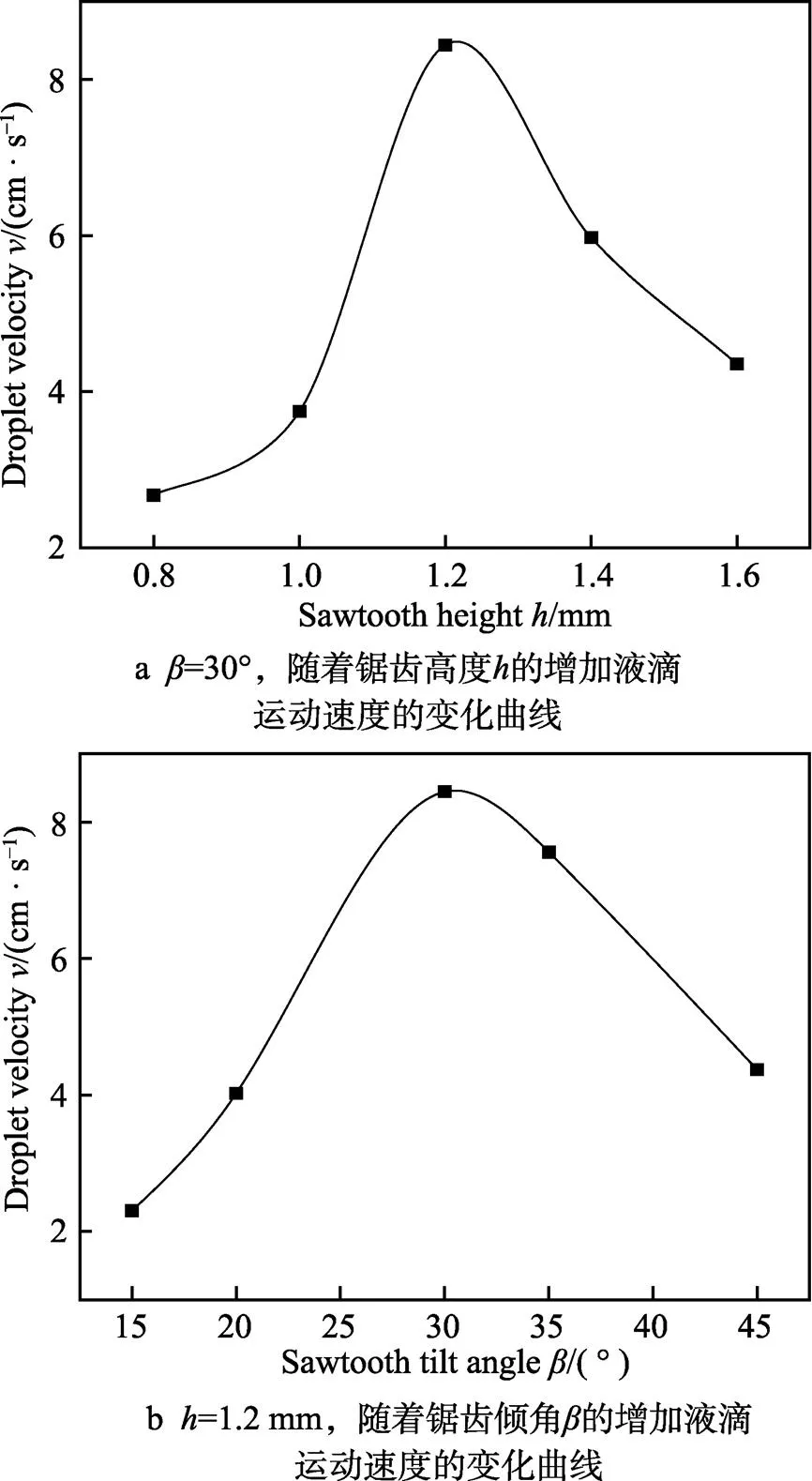
图7 锯齿表面参数对液滴运动速度的影响

3 结论

1）在非对称超疏水锯齿表面上，通过对锯齿表面施加一定条件的机械微振动，液滴在锯齿表面上会呈现不同的动态行为，即静止、定向蠕动、跳跃、破裂等行为。

2）由最优振幅和共振频率组成的最佳振动，可以使一定尺寸的液滴获得最佳的运动速度。同时，调整表面结构参数可促使液滴的运动速度加快，并且随着液滴体积的增加，液滴运动速度呈现先变快、再变慢的趋势。

3）针对液滴的定向蠕动行为，基于力学分析建立了液滴运动的物理模型。

[1] SUN D, BÖHRINGER K F. An Active Self-Cleaning Surface System for Photovoltaic Modules Using Anisotropic Ratchet Conveyors and Mechanical Vibration[J]. Micros­ystems & Nanoengineering, 2020, 6: 87.

[2] 杨华荣, 李梦, 赵欣, 等. 超疏水表面制备及其在防冰中的应用[J]. 新技术新工艺, 2021(10): 11-16.

YANG Hua-rong, LI Meng, ZHAO Xin, et al. Preparation of Super Hydrophobic Surface and Its Application in Anti-Icing[J]. New Technology & New Process, 2021(10): 11-16.

[3] 曹刚, 黄苏和, 李明升, 等. 润湿异性表面液滴定向运动研究进展[J]. 实验流体力学, 2021, 35(1): 67-85.

CAO Gang, HUANG Su-he, LI Ming-sheng, et al. Adva­nces in Research on Directional Movement of Droplets on Wetted Anisotropic Surfaces[J]. Journal of Experiments in Fluid Mechanics, 2021, 35(1): 67-85.

[4] LINKE H, ALEMÁN B J, MELLING L D, et al. Self- Propelled Leidenfrost Droplets[J]. Physical Review Letters, 2006, 96(15): 154502.

[5] 熊雪娇, 贾志海, 邓勇, 等. 微结构梯度能表面振动液滴的运动特性[J]. 上海交通大学学报, 2021, 55(4): 455-461.

XIONG Xue-jiao, JIA Zhi-hai, DENG Yong, et al. Motion Characteristics of Vibrated Droplets on Micropillared Surface with Gradient Energy[J]. Journal of Shanghai Jiao Tong University, 2021, 55(4): 455-461.

[6] LIU Chao-ran, SUN Jing, LI Jing, et al. Long-Range Spon­taneous Droplet Self-Propulsion on Wettability Gradient Surfaces[J]. Scientific Reports, 2017, 7: 7552.

[7] YANG Jing-tang, CHEN J C, HUANG K J, et al. Droplet Manipulation on a Hydrophobic Textured Surface with Roughened Patterns[J]. Journal of Microelectromech­anical Systems, 2006, 15(3): 697-707.

[8] SHENG Xian-liang, ZHANG J H. Directional Motion of Water Drop on Ratchet-Like Superhydrophobic Surfaces[J]. Applied Surface Science, 2011, 257(15): 6811-6816.

[9] HAO Peng-fei, LV C J, ZHANG X W, et al. Driving Liquid Droplets on Microstructured Gradient Surface by Mechanical Vibration[J]. Chemical Engineering Science, 2011, 66(10): 2118-2123.

[10] PRAKASH M, QUÉRÉ D, BUSH J W M. Surface Tension Transport of Prey by Feeding Shorebirds: The Capillary Ratchet[J]. Science, 2008, 320(5878): 931-934.

[11] JOSÉ B, DAVID Q. Self-Propelling Slugs[J]. Journal of Fluid Mechanics, 2002, 467: 101-127.

[12] ZHENG Yan-fen, CHENG Jiang, ZHOU Cai-long, et al. Droplet Motion on a Shape Gradient Surface[J]. Lang­muir: The ACS Journal of Surfaces and Colloids, 2017, 33(17): 4172-4177.

[13] ARTER J M, CLEAVER D J, TAKASHINA K, et al. Self-Propelling Leidenfrost Droplets on a Variable Topography Surface[J]. Applied Physics Letters, 2018, 113(24): 243704.

[14] 胡志英, 葛鹏, 张俊虎. 各向异性浸润表面在液体操控中的应用[J]. 分子科学学报, 2021, 37(5): 398-407.

HU Zhi-ying, GE Peng, ZHANG Jun-hu. Applications of Anisotropic Wetting Surfaces in Liquid Manipulation[J]. Journal of Molecular Science, 2021, 37(5): 398-407.

[15] SON C, JI Bing-qiang, PARK J, et al. A Magnetically Actuated Superhydrophobic Ratchet Surface for Droplet Manipulation[J]. Micromachines, 2021, 12(3): 325.

[16] 原子超, 詹海洋, 刘聪, 等. 浸润性表面液滴定向输运研究进展[J]. 表面技术, 2021, 50(8): 1-17.

YUAN Zi-chao, ZHAN Hai-yang, LIU Cong, et al. Research Progress on Droplet Directional Transport on Wetting Surfaces[J]. Surface Technology, 2021, 50(8): 1-17.

[17] YU Jiang-ping, LAO Jun-chao, CHU Dan-dan, et al. Reversible Photodriven Droplet Motion on Ti3C2MXene Film for Diverse Liquids[J]. ACS Applied Materials & Interfaces, 2020, 12(16): 19194-19200.

[18] LEI Wei, JIA Zhi-hai, HE Ji-chang, et al. Vibration-Induced Wenzel-Cassie Wetting Transition on Microstructured Hydrophobic Surfaces[J]. Applied Physics Letters, 2014, 104(18): 181601.

[19] BORMASHENKO E, POGREB R, WHYMAN G, et al. Vibration-Induced Cassie-Wenzel Wetting Transition on Rough Surfaces[J]. Applied Physics Letters, 2007, 90(20): 201917.

[20] CHAMAKOS N T, KARAPETSAS G, PAPATHANAS­IOU A G. How Asymmetric Surfaces Induce Directional Droplet Motion[J]. Colloids and Surfaces A: Physicoc­hemical and Engineering Aspects, 2016, 511: 180-189.

[21] DE MALEPRADE H, KEISER A, CLANET C, et al. Friction Properties of Superhydrophobic Ridges[J]. Journal of Fluid Mechanics, 2020, 890: A19.

[22] NAJI M, YELEKLI KIRICI E, JAVILI A, et al. Describ­ing Droplet Motion on Surface-Textured Ratchet Tracks with an Inverted Double Pendulum Model[J]. Langmuir: the ACS Journal of Surfaces and Colloids, 2021, 37(16): 4810-4816.

[23] JUNG Y C, BHUSHAN B. Dynamic Effects Induced Transition of Droplets on Biomimetic Superhydrophobic Surfaces[J]. Langmuir: the ACS Journal of Surfaces and Colloids, 2009, 25(16): 9208-9218.

[24] NOBLIN X, BUGUIN A, BROCHARD-WYART F. Vibrated Sessile Drops: Transition between Pinned and Mobile Contact Line Oscillations[J]. The European Physical Journal E, 2004, 14(4): 395-404.

Dynamic Characteristics of Vibrating Droplets on Superhydrophobic Ratchet Surfaces

,,,

(University of Shanghai for Science and Technology, Shanghai 200093, China)

Droplets show apparent dynamic properties on a superhydrophobic vibrating ratchet surface. The work aims to explore the motion mechanism and influencing factors of droplets in this process. In this paper, a physical model of droplet motion was developed and the effect of various parameters on dynamic behaviors of droplets was explored. In the experimental section, firstly, a series of asymmetric ratchet surfaces with a certain inclination and height were fabricated with aluminum sheets. Next, the ratchet surfaces were uniformly sprayed and dried with a hydrophobic coating, Glaco Soft 99, and the procedure was repeated several times until the surfaces had a stable superhydrophobicity. At this point, it was not necessary to consider the adhesion between the droplet and the ratchet surface. Finally, the ratchet surface was fixed to the shaking table, a drop of deionized water was placed on the surface, a certain amount of vibration was loaded, and the droplet motion was captured at a rate of 1000 fps with a high-speed camera (Fastec Imaging Hispec 3). The dynamic behavior of the vibrating droplet was observed and studied. It was found that within a certain vibration range, in which the frequency action range was 10-100 Hz and the amplitude action range was 0-2 mm, the vibrating droplet on the superhydrophobic ratchet surface exhibited four different behaviors, i.e., stationary, directional creep, jumping, and rupture behaviors, as the vibration amplitude increased. The experimental results showed that the fastest motion of the vibrating droplet on the superhydrophobic ratchet surface can reach 8 cm/s, which was much faster than the results of similar studies. Considering the continuity of droplet motion, this work investigated the directional creeping behavior of the droplet. During the motion of the droplet, experimental pictures were taken every 10 ms, and the contact angle at both ends of each picture and the center of mass of the droplet were measured. A physical model of droplet motion was proposed by considering the driving force and resistance during the droplet motion using mechanical analysis. The accuracy of the model was verified by repeating the experiments and obtaining experimental values agreeing with the theoretical values. With the help of the model, the effects of vibration characteristics parameters, ratchet parameters and droplet volume on droplet motion characteristics were analyzed. For a certain size of droplet, there is an optimal vibration acceleration consisting of resonant frequency and optimized amplitude, which can make the droplet achieve the fastest motion velocity under this condition. Also, the ratchet parameters affects the droplet motion velocity. By adjusting the angle and height of the ratchet to appropriate values, the droplet motion can run faster. Finally, the droplet volume also affects the droplet motion velocity. As the droplet volume increased, the droplet motion velocity showed a trend of increasing first and then decreasing. Therefore, adjusting the droplet volume to a proper value will help the droplet move faster. This work provides a method and theoretical support for the subsequent manipulation of droplet motion.It has various applications in some fields such as enhanced heat transfer, liquid transportation, and aerospace.

droplets; superhydrophobic; ratchet surfaces; vibration; directional drive

O647

A

1001-3660(2023)01-0278-07

10.16490/j.cnki.issn.1001-3660.2023.01.028

2022−01−17；

2022−04−25

2022-01-17；

2022-04-25

国家自然科学基金（51776128）

National Natural Science Foundation of China (51776128)

黄宝罗（1996—），男，硕士生，主要研究方向为功能材料在能源动力领域的应用。

HUANG Bao-luo (1996-), Male, Postgraduate, Research focus: application of functional materials in the field of energy and power.

贾志海（1975—），男，博士，教授，主要研究方向为功能材料在能源动力领域的应用。

JIA Zhi-hai (1975-), Male, Doctor, Professor, Research focus: application of functional materials in the field of energy and power.

黄宝罗, 贾志海, 康学良, 超疏水锯齿表面振动液滴的动态特性[J]. 表面技术, 2023, 52(1): 278-284.

HUANG Bao-luo, JIA Zhi-hai, KANG Xue-liang, et al. Dynamic Characteristics of Vibrating Droplets on Superhydrophobic Ratchet Surfaces [J]. Surface Technology, 2023, 52(1): 278-284.

责任编辑：彭颋